Perturbation Theory
Time Independent Perturbation Theory
Examples - Constant Perturbation
Examples - Linear Perturbation
Examples - Quadratic Perturbation
Time Dependent Perturbation Theory
Introduction
Perturbation theory is a cornerstone of quantum mechanics, offering a pragmatic framework for addressing problems that are otherwise analytically intractable. In the quantum realm, exact solutions to the Schrödinger equation are only known for a handful of idealized systems. However, real-world systems often involve interactions and complexities that defy straightforward solutions. Here, perturbation theory steps in as a vital tool, allowing physicists to explore the effects of small modifications to systems whose unperturbed states are well understood.
The importance of this theory extends beyond mere academic interest; it is pivotal in practical applications. For instance, perturbation theory aids in the understanding of atomic and molecular behavior under external influences, such as electromagnetic fields, which leads to essential insights in fields like spectroscopy, quantum chemistry, and materials science. This approach provides a systematic method to approximate the energies and states of quantum systems under slight disturbances, making it indispensable for predicting the behavior of physical systems at the atomic level.
Moreover, perturbation theory’s flexibility and general applicability make it a universal tool across various subfields of physics. Whether adjusting models to include weak interactions in particle physics or predicting the impact of slight deformations in solid-state physics, perturbation theory remains a fundamental method for bridging the gap between ideal models and real-world phenomena. Thus, its role in advancing both theoretical understanding and technological innovation in quantum mechanics cannot be overstated.
Perturbation theory is particularly useful and practically applicable in quantum mechanics because the external forces typically applied in experimental and practical scenarios are often much smaller compared to the intrinsic forces within the atoms. This disparity in scale allows perturbation theory to effectively approximate how these small external changes influence the system.
Atoms are bound by extremely strong internal forces, such as the electromagnetic force holding electrons in orbit around the nucleus. These internal forces are several orders of magnitude greater than most external perturbations that can be practically applied, such as weak magnetic or electric fields in laboratory settings. For instance, the electric field within a hydrogen atom is on the order of 10^9 volts per meter, vastly exceeding the external fields typically used in experiments, which are much weaker.
This significant difference in magnitude means that the external perturbation does not drastically alter the overall structure of the atom but instead induces slight shifts or splits in energy levels—subtle effects that perturbation theory can calculate with reasonable accuracy. The theory treats the effect of the external perturbation as a small correction to the known results of the unperturbed system. By focusing only on the first few terms in the expansion, significant and meaningful results about the system’s behavior under the influence of an external perturbation can be derived without the need for solving the complete and often intractable problem from scratch.
Therefore, the practical applicability of perturbation theory lies in its ability to provide insights into how even minor external influences can lead to observable phenomena, such as spectral line splitting in the presence of an electric field (Stark effect), with a relatively simple mathematical approach compared to the complexities of solving a fully perturbed quantum system. This makes perturbation theory not only a theoretical tool but a practical one for predicting and understanding the subtle changes in quantum systems exposed to external forces.
Perturbation theory is not only a powerful tool in quantum mechanics but also plays a significant role in classical physics. Its versatility allows it to be applied to a variety of classical systems where systems can be modeled as perturbations of simpler, solvable problems.
A classic example from classical physics where perturbation theory proves useful is the motion of a pendulum. In its simplest form, the motion of a pendulum—assuming small angular displacements—is described by a linear differential equation, leading to simple harmonic motion. The equation of motion for a pendulum under the small angle approximation (\theta \ll 1 radian) is given by:
\ddot{\theta} + \frac{g}{L} \theta = 0
Here, \theta is the angular displacement, g is the acceleration due to gravity, and L is the length of the pendulum. This model predicts that the period of the pendulum is independent of the amplitude of oscillation, which is true only for small angles.
However, when the angular displacement is not small, the restoring force due to gravity becomes non-linear, and the simple harmonic motion approximation no longer holds. The true equation of motion without the small angle approximation is:
\ddot{\theta} + \frac{g}{L} \sin(\theta) = 0
This equation cannot be solved exactly using elementary functions. When the angle \theta becomes large, the non-linear term \sin(\theta) deviates significantly from the linear term \theta, requiring higher order corrections. Perturbation theory can be applied here by considering the term \sin(\theta) - \theta as a perturbation to the linear system. By expanding \sin(\theta) in a Taylor series around \theta = 0 and keeping higher order terms, one can use perturbation theory to calculate corrections to the simple harmonic motion approximation:
\sin(\theta) \approx \theta - \frac{\theta^3}{6} + \cdots
This expansion introduces higher order corrections to the motion, leading to more accurate descriptions of the pendulum’s period and amplitude dependence, particularly for larger angles. The inclusion of these higher order terms adjusts the period, showing that it actually increases with larger amplitudes, a result that aligns well with experimental observations and cannot be captured by the linear model alone.
Thus, perturbation theory extends the applicability of classical models by providing a systematic way to account for non-linear effects and more complex interactions that are otherwise too difficult to handle analytically. This example clearly illustrates how perturbation theory bridges the gap between idealized models and the complexities of real-world phenomena, both in classical and quantum contexts.
Time independent perturbation theory
I’ll begin setting up perturbation theory; since this theory is frequently used to determine how the eigenenergies of a quantum mechanical system are affected by a small perturbation to the system we will explore how energy eigenvalues and eigenfunctions are impacted under this theory. Specifically, I will consider modifications to the system’s Hamiltonian to understand the effects of small changes on the system.
I’ll describe this process as adding a perturbing Hamiltonian to the system’s existing Hamiltonian and I will focus on problems that do not change with time, referring to this approach as time-independent or stationary perturbation theory. the discussion will be limited to scenarios where the energy states are non-degenerate, meaning each eigenvalue corresponds to a unique eigenfunction.
We assume that the system start in an unperturbed state \mathbf H_0 in which the eigenvalues and eigenfunctions are known:
\mathbf H_0 | \psi_n \rangle = E_n | \psi_n \rangle
Then we introduce a parameter \lambda, a dimensionless parameter that can take continuous values from 0 (no perturbation) to 1 (full perturbation) and the changes can be written as a power series function of \lambda, \lambda^2, \dots
We imagine now that the perturbed system has some additional terms in the Hamiltonian \mathbf H_p (the perturbing Hamiltonian) and is written as \lambda\,\mathbf H_p; \lambda is a placeholder useful to keep track of the correction, and it is possible to set \lambda=1 at the end.
The perturbed Schrödinger equation can be written as:
\left(\mathbf H_0 + \lambda \mathbf H_p\right)| \phi^{(n)} \rangle = E | \phi^{(n)} \rangle
The eigenstates |\phi^{(n)}\rangle and eigenvalues E_n can be expanded in powers of \lambda:
|\phi^{(n)}\rangle = |\phi^{(0)}\rangle + \lambda |\phi^{(1)}\rangle + \lambda^2 |\phi^{(2)}\rangle + \cdots
Likewise for the eigenvalues E:
E = E^{(0)} + \lambda E^{(1)} + \lambda^2 E^{(2)} + \cdots
Substituting into the Schrödinger equation:
\begin{aligned} \left(\mathbf H_0 \right. & + \left. \lambda \mathbf H_p\right) \left( |\phi^{(0)}\rangle + \lambda |\phi^{(1)}\rangle + \lambda^2 |\phi^{(2)}\rangle + \cdots \right) \\ & =\left( E^{(0)} + \lambda E^{(1)} + \lambda^2 E^{(2)} + \cdots \right) \left( |\phi^{(0)}\rangle + \lambda |\phi^{(1)}\rangle + \lambda^2 |\phi^{(2)}\rangle + \cdots \right) \end{aligned}
Both sides of the equation resemble a power series in \lambda. Each function in the equation has a specific value at any given point in space. When operated upon by this operator, the function yields a value at that point. On the right-hand side, we directly have the values of these functions at that point in space. Thus, at any point, there is a number derived from the left-hand side and a corresponding number from the right-hand side.
This setup results in a straightforward equation between two numbers, expressible as power series. Due to the uniqueness of power series expansions, this condition must hold for every value of lambda within a specific convergence range, such as between 0 and 1, confirming the uniqueness and equality of power series.
It is therefore possible to equate terms of like powers of \lambda on both sides of the equation.
At the zeroth order in \lambda, the equation simplifies to:
\mathbf{H}_0 |\phi^{(0)}\rangle = E^{(0)} |\phi^{(0)}\rangle
This equation states that |\phi^{(0)}\rangle and E^{(0)} are the eigenstates and eigenvalues of the unperturbed Hamiltonian \mathbf{H}_0.
If the starting point is this unperturbed Hamiltonian, it is possible to write | \psi_n \rangle in place of |\phi^{(0)}\rangle and E_n in place of E^{(0)}:
\begin{aligned} \left(\mathbf H_0 \right. & + \left. \lambda \mathbf H_p\right) \left( |\psi_n\rangle + \lambda |\phi^{(1)}\rangle + \lambda^2 |\phi^{(2)}\rangle + \cdots \right) \\ & =\left( E_n + \lambda E^{(1)} + \lambda^2 E^{(2)} + \cdots \right) \left( |\phi^{(0)}\rangle + \lambda |\phi^{(1)}\rangle + \lambda^2 |\phi^{(2)}\rangle + \cdots \right) \end{aligned}
The zeroth order in \lambda gives:
\mathbf{H}_0 |\psi_n\rangle = E_n|\psi_n\rangle
For the first order in \lambda, we have:
\mathbf{H}_0 |\phi^{(1)}\rangle + \mathbf{H}_p |\psi_n\rangle = E_n |\phi^{(1)}\rangle + E^{(1)} |\psi_n\rangle
For the second order in \lambda:
\mathbf{H}_0 |\phi^{(2)}\rangle + \mathbf{H}_p |\phi^{(1)}\rangle = E_n |\phi^{(2)}\rangle + E^{(1)} |\phi^{(1)}\rangle + E^{(2)} |\psi_n\rangle The zeroth term can be rewritten as (there is an implicit identity operator \mathbf I acting on the energy):
\mathbf{H}_0 |\psi_n\rangle - E_n|\psi_n\rangle = 0
The first order can be rewritten as:
\left(\mathbf{H}_0 - E_n \right)|\phi^{(1)}\rangle = \left(E^{(1)} - \mathbf{H}_p \right) |\psi_n\rangle And the second order as:
\left(\mathbf{H}_0 - E_n \right)|\phi^{(2)}\rangle = \left( E^{(1)} - \mathbf{H}_p \right)|\phi^{(1)}\rangle + E^{(2)} |\psi_n\rangle
First order correction
It is now possible to calculate the various term, starting from the first order and premultiplying with \langle \psi_n |:
\langle \psi_n |\left(\mathbf{H}_0 - E_n \right)|\phi^{(1)}\rangle = \langle \psi_n |\left(E^{(1)} - \mathbf{H}_p \right) |\psi_n\rangle
Starting from the left hand side:
\langle \psi_n |\left(\mathbf{H}_0 - E_n \right)|\phi^{(1)}\rangle = \left(\langle \psi_n |\mathbf{H}_0 - E_n \right)\phi^{(1)}\rangle = \left(\langle \psi_n |E_n - E_n \right)\phi^{(1)}\rangle = 0
On the right hand side:
\langle \psi_n |\left(E^{(1)} - \mathbf{H}_p \right) |\psi_n\rangle = \left(\langle \psi_n |E^{(1)} - \mathbf{H}_p \right) |\psi_n\rangle = E^{(1)} - \langle \psi_n | \mathbf{H}_p |\psi_n\rangle
So the first order correction to the energy is:
E^{(1)} = \langle \psi_n | \mathbf{H}_p |\psi_n\rangle
Once the correction to the energy is computed, it is possible to compute the correction for the wavefunction | \phi^{(1)} \rangle, expanding it in the basis set \{|\psi_i\rangle\}:
| \phi^{(1)} \rangle = \sum_i a_i^{(1)} | \psi_i \rangle
Premultiplying now the equation by \langle \psi_i | and using this expansion, starting from the left hand side:
\begin{aligned} \langle \psi_i |\left(\mathbf{H}_0 - E_n \right)|\phi^{(1)}\rangle & = \langle \psi_i |\left(\mathbf{H}_0 - E_n \right)|\phi^{(1)}\rangle = \left(\langle \psi_i | \mathbf{H}_0\right) | \phi^{(1)} \rangle - E_n \langle \psi_i | \phi^{(1)} \rangle \\ & = \left(E_i - E_n \right)\langle \psi_i | \phi^{(1)} \rangle = \left(E_i - E_n \right)\langle \psi_i | \sum_i a_i^{(1)} | \psi_i \rangle \\ & = \left(E_i - E_n \right) \sum_i a_i^{(1)} \langle \psi_i | \psi_i \rangle = \left(E_i - E_n \right) a_i^{(1)} \end{aligned}
On the right hand side:
\langle \psi_i |\left(E^{(1)} - \mathbf{H}_p \right) |\psi_n\rangle = E^{(1)}\langle \psi_i | \psi_n\rangle - \langle \psi_i | \mathbf{H}_p | \psi_n\rangle = E^{(1)} - \langle \psi_i | \mathbf{H}_p | \psi_n\rangle
Equating the two sides:
\left(E_i - E_n \right) a_i^{(1)} = E^{(1)}\langle \psi_i | \psi_n\rangle - \langle \psi_i | \mathbf{H}_p | \psi_n\rangle = E^{(1)} - \langle \psi_i | \mathbf{H}_p | \psi_n\rangle
With the assumption that there are no degenerate energy eigenvalues, for i\ne n, then:
a_i^{(1)} = \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i}
for i=n
\left(E_n - E_n \right) a_n^{(1)} = 0a_i^{(1)} = E^{(1)}\langle \psi_n | \psi_n\rangle - \langle \psi_n | \mathbf{H}_p | \psi_n\rangle = E^{(1)} - E^{(1)} = 0
This result is not dependent from a_n^{(1)} and therefore a convenient choice is to take:
a_n^{(1)} = 0
which is the choice to make the perturbation |\phi^{(1)}\rangle orthogonal to | \psi_n\rangle. The same happen to higher order equations, and therefore the choice to simplify the computation will always be to take the perturbation orthogonal.
Putting all together, the first order correction to the wavefunction is:
| \phi^{(1)} \rangle = \sum_{i \ne n} a_i^{(1)} | \psi_i \rangle, \quad a_i^{(1)} = \sum_{i\ne n} \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i}
which is coupled with the first order correction to the energy:
E^{(1)} = \langle \psi_n | \mathbf{H}_p |\psi_n\rangle
Second order correction
The process is similar to compute the second order correction (and would be the same for higher order), premultiplying with \langle \psi_n |:
\langle \psi_n | \left(\mathbf{H}_0 - E_n \right)|\phi^{(2)}\rangle = \left( E^{(1)} - \mathbf{H}_p \right)|\phi^{(1)}\rangle + E^{(2)} |\psi_n\rangle
Starting from the left-hand side:
\begin{aligned} \langle \psi_n | \left(\mathbf{H}_0 - E_n \right)|\phi^{(2)}\rangle &= \left(\langle \psi_n | \mathbf{H}_0 - E_n \right) |\phi^{(2)}\rangle \\ &= \left(E_n - E_n \right) \langle \psi_n | \phi^{(2)} \rangle \\ &= 0 \end{aligned}
On the right-hand side:
\langle \psi_n |\left(E^{(1)} - \mathbf{H}_p \right) |\phi^{(1)}\rangle + E^{(2)} \langle \psi_n|\psi_n\rangle = E^{(1)} \langle \psi_n |\phi^{(1)}\rangle - \langle \psi_n | \mathbf{H}_p |\phi^{(1)}\rangle + E^{(2)}
Rearranging:
E^{(2)} = \langle \psi_n | \mathbf{H}_p |\phi^{(1)}\rangle - E^{(1)} \langle \psi_n |\phi^{(1)}\rangle
Using the orthogonality of the |\psi_i\rangle basis:
E^{(2)} = \langle \psi_n | \mathbf{H}_p |\phi^{(1)}\rangle
This is the second-order correction to the energy. Using the result previously obtained:
E^{(2)} = \langle \psi_n | \mathbf{H}_p | \left( \sum_{i\ne n} \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i} | \psi_i \rangle \right)
To obtain the second-order correction to the wavefunction |\phi^{(2)}\rangle, we expand it in the basis set \{|\psi_i\rangle\}:
|\phi^{(2)}\rangle = \sum_i a_i^{(2)} |\psi_i\rangle
Premultiplying by \langle \psi_i | and using the expansions:
\begin{aligned} \langle \psi_i | \left(\mathbf{H}_0 - E_n \right)|\phi^{(2)}\rangle &= \left(E_i - E_n \right) \langle \psi_i | \phi^{(2)} \rangle \\ &= \left(E_i - E_n \right) \sum_j a_j^{(2)} \langle \psi_i | \psi_j \rangle \\ &= \left(E_i - E_n \right) a_i^{(2)} \end{aligned}
On the right hand side:
\begin{aligned} \langle \psi_i |\left( E^{(1)} - \mathbf{H}_p \right)|\phi^{(1)}\rangle + E^{(2)} \langle \psi_i |\psi_n\rangle & = E^{(1)} \langle \psi_i |\phi^{(1)}\rangle - \langle \psi_i |\mathbf{H}_p |\phi^{(1)}\rangle + E^{(2)} \langle \psi_i |\psi_n\rangle \\ & = E^{(1)} a_i^{(1)} - \sum_{i \ne n} a^{(1)} \langle \psi_i |\mathbf{H}_p |\psi_i\rangle + E^{(2)} \langle \psi_i |\psi_n\rangle \end{aligned}
for i=n, using the orthogonality of | \psi_n \rangle and |\phi^{(1)}\rangle:
\left(E_n - E_n \right) a_n^{(2)} = 0a_n^{(2)} = E^{(1)} \langle \psi_n |\phi^{(1)}\rangle - \langle \psi_n |\mathbf{H}_p |\phi^{(1)}\rangle + E^{(2)} \langle \psi_n |\psi_n\rangle = 0 - E^{(2)} + E^{(2)} = 0
This result is not dependent from a_n^{(2)} and therefore a convenient choice is to take:
a_n^{(2)} = 0
which is the choice to make the perturbation |\phi^{(2)}\rangle also orthogonal. Then for i \ne j the formula simplifies:
\langle \psi_i |\left( E^{(1)} - \mathbf{H}_p \right)|\phi^{(1)}\rangle + E^{(2)} \langle \psi_i |\psi_n\rangle = E^{(1)} a_i^{(1)} - \sum_{i \ne n} a^{(1)} \langle \psi_i |\mathbf{H}_p |\psi_i\rangle
Therefore:
\left(E_i - E_n \right) a_i^{(2)} = E^{(1)} a_i^{(1)} - \sum_{i \ne n} a^{(1)} \langle \psi_i |\mathbf{H}_p |\psi_i\rangle
Putting all together, the second order correction to the wavefunction is:
|\phi^{(2)}\rangle = \sum_{i \ne n} a_i^{(2)} |\psi_i\rangle, \quad a_i^{(2)} = \sum_{i \ne n} \frac{a^{(1)}\langle \psi_i |\mathbf{H}_p |\psi_i\rangle}{E_n - E_i} - \frac{E^{(1)} a_i^{(1)}}{E_n - E_i}
which is coupled with the second order correction to the energy:
E^{(2)} = \langle \psi_n | \mathbf{H}_p |\phi^{(1)}\rangle = \langle \psi_n | \mathbf{H}_p | \left( \sum_{i\ne n} \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i} | \psi_i \rangle \right)
Constant perturbation
Let’s suppose that the perturbation is a constant value independent from the position:
\mathbf H_p = E_c Applying the formulas for the first order, starting from the energy:
E^{(1)} = \langle \psi_n | \mathbf{H}_p |\psi_n\rangle = E_c \langle \psi_n |\psi_n\rangle = E_c
The correction for the wavefunction is:
| \phi^{(1)} \rangle = \sum_{i \ne n} a_i^{(1)} | \psi_i \rangle, \quad a_i^{(1)} = \sum_{i\ne n} \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i} = E_c \sum_{i\ne n} \frac{\langle \psi_i | \psi_n\rangle}{E_n - E_i} = 0
So, given any eigenstate \psi_n, the first order correction for the energy is constant and there is no first order correction for the wavefunction.
Applying the formulas for the second order, starting from the energy:
E^{(2)} = \langle \psi_n | \mathbf{H}_p |\phi^{(1)}\rangle = 0
The correction for the wavefunction is:
|\phi^{(2)}\rangle = \sum_{i \ne n} a_i^{(2)} |\psi_i\rangle, \quad a_i^{(2)} = \sum_{i \ne n} \frac{a^{(1)}\langle \psi_i |\mathbf{H}_p |\psi_i\rangle}{E_n - E_i} - \frac{E^{(1)} a_i^{(1)}}{E_n - E_i} = E_c \sum_{i \ne n} \frac{a^{(1)}\langle \psi_i |\psi_i\rangle}{E_n - E_i} - 0 = 0
So, given any eigenstate \psi_n, there is no second order correction for the energy nor for the wavefunction.
Linear perturbation
Considering a one dimensional problem in the x direction that in the unperturbed state is symmetrical with respect to the x axis (for example a particle in a box, express in dimensionless units), let’s suppose to perturb the system with an applied perturbation Hamiltonian that corresponds to an odd function, for example a linear perturbation, in a symmetrical way (so in this case relative to the center of the box). Since the wavefunctions are known, it is possible to compute the solution exactly for this problem.
The example of the applied electric field (here) fits well in this framework so the perturbation that will be used is the same:
\mathbf H_p = f\left(\xi-\frac{1}{2}\right)
So the perturbed Hamiltonian is:
\mathbf H = -\frac{1}{\pi^2}\frac{\mathrm d^2}{\mathrm d\xi^2} + f\left(\xi-\frac{1}{2}\right)
Once computed in general, we will apply to f=3 to compare the results with the analytical solution. The associated eigenenergies are:
E_n = n^2 And the eigenfunctions:
\phi_n(\xi) = \sqrt 2 \sin\left(n\pi\xi\right)
Applying the formulas for the first order, starting from the energy:
\begin{aligned} E^{(1)} & = \langle \psi_n | \mathbf{H}_p |\psi_n\rangle = 2f \int_0^1 \left(\xi - \frac{1}{2}\right) \sin^2\left(n\pi\xi\right) \, \mathrm{d}\xi \\ & = 2f \left[ \frac{x^2}{4} - \frac{x}{4} - \frac{x \sin(4 \pi x)}{8 \pi} + \frac{\sin(4 \pi x)}{16 \pi} - \frac{\cos(4 \pi x)}{32 \pi^2} \right] \bigg|_0^1 = 0 \end{aligned}
There is no correction for any n, and that can be explained by symmetry as \sin^2(x) is an even function and f\left(\xi-\frac{1}{2}\right) is odd so every contribution on the first half of the interval is canceled by the second half.
The correction for the wavefunction is:
| \phi^{(1)} \rangle = \sum_{i \ne n} a_i^{(1)} | \psi_i \rangle, \quad a_i^{(1)} = \sum_{i\ne n} \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i} = 2f \sum_{i\ne n} \frac{1}{E_n - E_i} \int_0^1 \sin\left(i\pi\xi\right)\left(\xi - \frac{1}{2}\right) \sin\left(n\pi\xi\right) \, \mathrm{d}\xi
This integral is:
2f\left(\frac{-4in + \sin(i\pi)\left((i-n)n(i+n)\pi\cos(n\pi) + 2(i^2 + n^2)\sin(n\pi)\right) + i\cos(i\pi)\left(4n\cos(n\pi) + (-i+n)(i+n)\pi\sin(n\pi)\right)}{2(i^2 - n^2)^2\pi^2} \right)
This function exhibits the same symmetry on the interval [0,1] and therefore i and n need to have different parity to give a contribution different from zero.
Considering now the first four energy level, the coefficients can be computed:
\begin{array}{|c|cccccccccc|} \hline | \psi_1 \rangle & 0 & 0.18 & 0 & 0.003 & 0 & 0 & 0 & 0 & -0 & 0 \\ \hline | \psi_2 \rangle & -0.18 & 0 & 0.117 & -0 & 0.003 & 0 & 0 & -0 & 0 & -0 \\ \hline | \psi_3 \rangle & -0 & -0.117 & 0 & 0.085 & 0 & 0.002 & 0 & 0 & -0 & 0 \\ \hline | \psi_4 \rangle & -0.003 & 0 & -0.085 & 0 & 0.067 & -0 & 0.002 & -0 & 0 & -0 \\\hline \end{array}
These compare well with the finite matrices (here), and for example the coefficient a_{2}^{(1)} (0.18) for | \psi_1 \rangle compares well to the -0.174 from the finite matrices (the sign is not relevant as the probability density square the values). It is also noticeable that the coefficients go to zero fairly quickly, so it is not necessary to compute many of them.
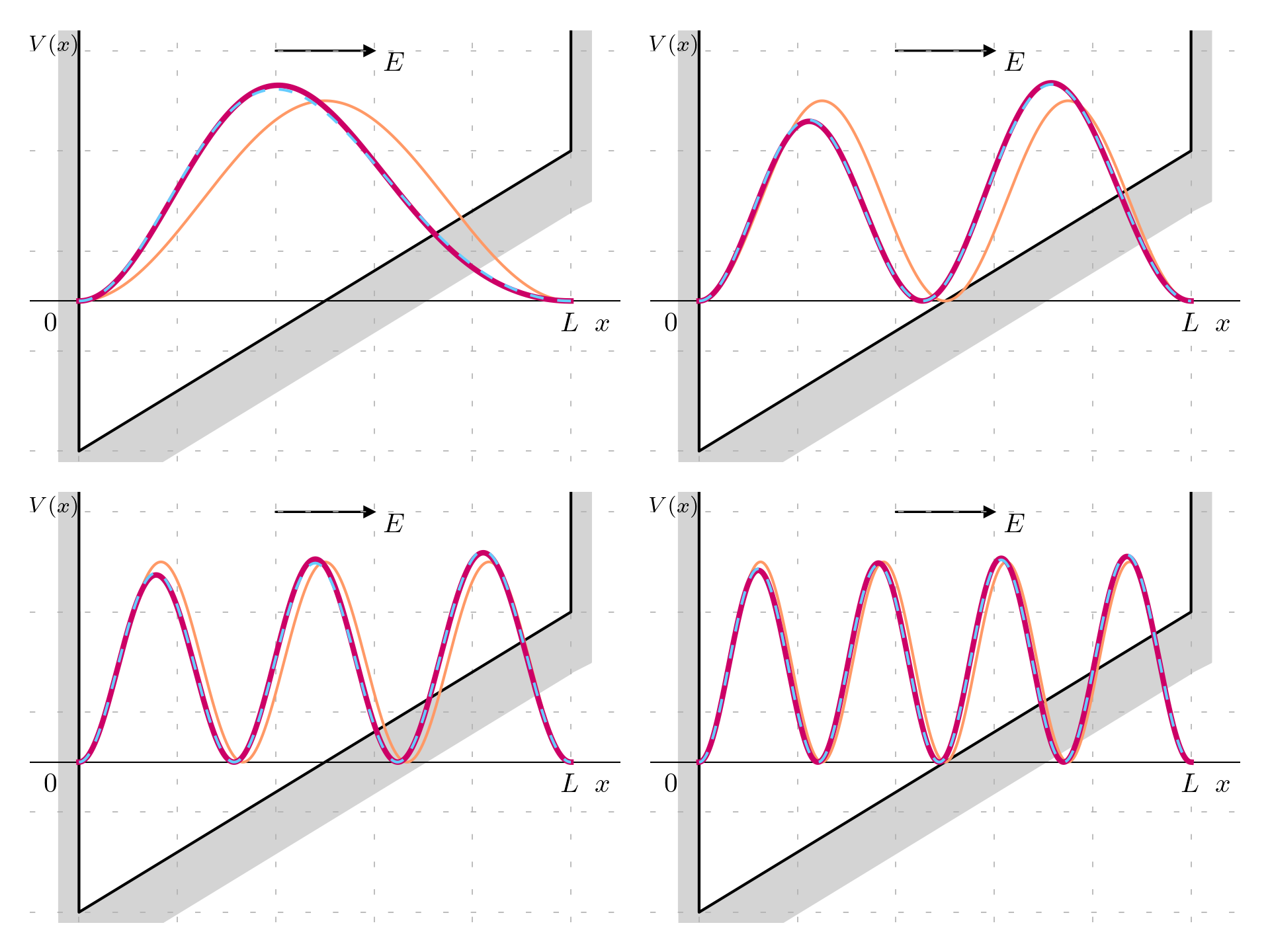
Graphically these solutions can be plot and these behavior discovered; it worth notice that the solution from the perturbation theory are not normalized, so these were additionally numerically normalized; in any case since the perturbation is small, also the wavefunction is almost normalized already in any case.
To get a correction to the energy it is necessary to go to the second order:
\begin{aligned} E^{(2)} & = \langle \psi_n | \mathbf{H}_p | \left( \sum_{i\ne n} \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i} | \psi_i \rangle \right) = \sum_{i\ne n} \frac{\left| \langle \psi_i | \mathbf{H}_p | \psi_n\rangle\right|^2}{E_n - E_i} \\ & = \sum_{i\ne n} \frac{\left| \langle \psi_i |f\left(\xi-\frac{1}{2}\right) | \psi_n\rangle \right|^2}{E_n - E_i} = f^2\sum_{i\ne n} \frac{\left| \langle \psi_i |\left(\xi-\frac{1}{2}\right)| \psi_n\rangle \right|^2}{E_n - E_i} \end{aligned} Once this is computed, the correction to the energy can be computed:
\eta_n \approx E_n + E^{(1)} + E^{(2)} = E_n + E^{(2)}
That can be numerically evaluated (taking in this case too a finite number of basis wavefunction, as the coefficients goes to zero rapidly):
\begin{array}{|c|c|c|} \hline \text{correction} & \eta_{approx} & \eta_{exact} \\ \hline -0.09747 & 0.90253 & 0.90419 \\ 0.02906 & 4.02906 & 4.02746 \\ 0.01732 & 9.01732 & 9.01726 \\ 0.01061 & 16.01061 & 16.0106 \\ \hline \end{array}
The result are quite close to the exact solutions.
A benefit of the perturbation theory is that give approximation formulas that can be reused for different value of the field (as in the formulas it was possible to pull out from the coefficient f for the wavefunction correction and f^2 for the energy correction).
Quadratic perturbation
Let’s consider the same infinite potential well, but this time assuming a quadratic perturbation:
\mathbf H_p = c\left(\xi-\frac{1}{2}\right)^2 This is centered in the middle of the well for reuse most of the framework built in the previous example; the perturbed Hamiltonian is:
\mathbf H = -\frac{1}{\pi^2}\frac{\mathrm d^2}{\mathrm d\xi^2} + f\left(\xi-\frac{1}{2}\right)^2
Applying the formulas for the first order, starting from the energy:
\begin{aligned} E^{(1)} & = \langle \psi_n | \mathbf{H}_p |\psi_n\rangle = 2c \int_0^1 \left(\xi - \frac{1}{2}\right)^2 \sin^2\left(n\pi\xi\right) \, \mathrm{d}\xi \\ & = 2c \left[ \frac{2 \pi n (\pi^2 n^2 - 3) + (6 - 3 \pi^2 n^2) \sin(2 \pi n) - 6 \pi n \cos(2 \pi n)}{48 \pi^3 n^3} \right] \end{aligned}
For the first four values:
\begin{aligned} & E_1^{(1)} = 2c \times 0.01634 \\ & E_2^{(2)} = 2c \times 0.03533 \\ & E_3^{(3)} = 2c \times 0.03885 \\ & E_4^{(4)} = 2c \times 0.04008 \end{aligned}
The correction for the wavefunction is:
| \phi^{(1)} \rangle = \sum_{i \ne n} a_i^{(1)} | \psi_i \rangle, \quad a_i^{(1)} = \sum_{i\ne n} \frac{\langle \psi_i | \mathbf{H}_p | \psi_n\rangle}{E_n - E_i} = 2c \sum_{i\ne n} \frac{1}{E_n - E_i} \int_0^1 \sin\left(i\pi\xi\right)\left(\xi - \frac{1}{2}\right)^2 \sin\left(n\pi\xi\right) \, \mathrm{d}\xi
The integral
I_c = \int_0^1 \sin\left(i\pi\xi\right)\left(\xi - \frac{1}{2}\right)^2 \sin\left(n\pi\xi\right) \, \mathrm{d}\xi
is computed to be:
\begin{aligned} I_c = \frac{1}{4 (i - n)^3 (i + n)^3 \pi^3} & \bigg[n \left(i^4 \pi^2 + n^2 (-8 + n^2 \pi^2) - 2 i^2 (12 + n^2 \pi^2)\right) \cos(n \pi) \sin(i \pi) \\ & - i \cos(i \pi) \left(8 n (-i^2 + n^2) \pi \cos(n \pi) + \left(i^4 \pi^2 + n^2 (-24 + n^2 \pi^2) \right. \right. \\ & \left. \left. - 2 i^2 (4 + n^2 \pi^2)\right) \sin(n \pi)\right) + 4 (i^2 - n^2) \pi \left(2 i n + (i^2 + n^2) \sin(i \pi) \sin(n \pi)\right)\bigg] \end{aligned}
The contribution to | \phi^{(1)} \rangle can be analyzed with parity considerations, as the perturbing Hamiltonian is even, and depending from the parity of the eigenfunction | \psi_n \rangle of the starting state, the product:
\langle \psi_i | \mathbf{H}_p | \psi_n\rangle is even or odd and therefore the integral on the interval [0,1] might be zero. As example, it is possible to the computed results of the integral for i = 1, 2, 3, 4 and n = 1, 2, 3, 4 (excluding by construction i = n):
\begin{array}{ccccc} \text{i \ n} & 1 & 2 & 3 & 4 \\ \hline 1 & 0 \, (i \ne n) & 0 & \frac{3}{16\pi^2} & 0 \\ 2 & 0 & 0 \, (i \ne n) & 0 & \frac{2}{9\pi^2} \\ 3 & \frac{3}{16\pi^2} & 0 & 0 \, (i \ne n) & 0 \\ 4 & 0 & \frac{2}{9\pi^2} & 0 & 0 \, (i \ne n) \\ \end{array}
which show the described behavior.
Time dependent perturbation theory
Time-dependent perturbation theory is a crucial tool in quantum mechanics for analyzing systems exposed to perturbations that vary with time. This approach is particularly useful when dealing with small, time-varying disturbances in a system’s Hamiltonian. Its main advantage is providing a manageable method to calculate the system’s response without directly solving the time-dependent Schrödinger equation, which can be complex and computationally intensive.
It can be useful in scenarios where electromagnetic fields vary with time, such as when materials are exposed to light beams or for predicting the probability of transitions between quantum states due to external perturbations or for understanding processes like the absorption or emission of light by atoms or molecules.
As for the time independent perturbation theory, it is a series of successive approximations and can give useful insights depending from the order considered: the first order is sufficiently accurate for weak perturbation, while higher order might be necessary for stronger perturbations or when the effect is nonlinear, as for example in higher-order effect of electric polarization in materials.
In the time dependent perturbation theory, the objective is to predict how the system is going to change in time and therefore there won’t be eigenstates as results; the chosen basis set will still be chosen to be the energy eigenfunction of the unperturbed problem, but this time the output will be how the coefficients of the basis functions will be varying with time, and, once the coefficients are known, the wavefunction and all the variables of interest can be computed at any point in time.
We assume that the system start in an unperturbed state \mathbf H_0 in which the eigenvalues and eigenfunctions are known and which is not changing with time:
\mathbf H_0 | \psi_n \rangle = E_n | \psi_n \rangle
We imagine now that the perturbed system has some additional terms in the Hamiltonian \mathbf H_p(t) (the perturbing Hamiltonian) the time dependent Schrödinger equation can be written as:
i\hbar\frac{\partial}{\partial t} | \Psi \rangle = \mathbf H | \Psi \rangle
with:
\mathbf H_0 + \mathbf H_p(t)
We assumed that the unperturbed Hamiltonian \mathbf H_0 could be solved (it is time independent) and the time dependent solution can be expanded in this basis:
| \Psi \rangle = \sum_j a_j(t)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle
The time dependent term of the unperturbed Hamiltonian has been explicitly separated (|\psi_j \rangle it is time independent), and the expansion coefficients are time dependent; substituting in the time dependent Schrödinger equation:
\sum_j \left( i\hbar \dot a_j(t) + E_ja_j(t)\right)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle = \sum_j a_j(t) \left(\mathbf H_0 + \mathbf H_p(t) \right)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle
where \dot a_j(t) \equiv \frac{\partial a_j(t)}{\partial t} is how the coefficient are varying with time; since \mathbf H_0 | \psi_n \rangle = E_n | \psi_n \rangle:
\sum_j \left( i\hbar \dot a_j(t) + E_ja_j(t)\right)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle = \sum_j a_j(t) \left(E_j + \mathbf H_p(t) \right)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle
so the expression simplify as:
\sum_j i\hbar \dot a_j(t)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle = \sum_j a_j(t) \mathbf H_p(t) e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle
Pre-multiplying for a specific energy eigenfunction \langle \psi_n|:
\begin{aligned} & \langle \psi_n | \sum_j i\hbar \dot a_j(t)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle = \langle \psi_n | \sum_j a_j(t) \mathbf H_p(t) e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle \\ & i\hbar \dot a_n(t)e^{-\frac{iE_n}{\hbar}} = \sum_j a_j(t) e^{-\frac{iE_jt}{\hbar}} \langle \psi_n | \mathbf H_p(t) | \psi_j \rangle \end{aligned}
Then we introduce a parameter \lambda, a dimensionless parameter that can take continuous values from 0 (no perturbation) to 1 (full perturbation) and the changes can be written as a power series function of \lambda, \lambda^2, \dots and the perturbed Hamiltonian can be written as \lambda \mathbf H_p. The coefficient can be expanded in power series as:
a_j = a_j^{(0)} + \lambda a_j^{(1)} + \lambda^2 a_j^{(2)} + \dots
Substituting in the Schrödinger equation:
i\hbar \left(\dot a_n^{(0)} + \lambda \dot a_n^{(1)} + \lambda^2 \dot a_n^{(2)} + \dots \right)e^{-\frac{iE_n}{\hbar}} = \sum_j \left(a_j^{(0)} + \lambda a_j^{(1)} + \lambda^2 a_j^{(2)} + \dots \right) e^{-\frac{iE_jt}{\hbar}} \langle \psi_n | \lambda \mathbf H_p(t) | \psi_j \rangle
It is then possible to equate terms of like powers of \lambda on both sides of the equation.
At the zeroth order in \lambda, the equation simplifies to:
\dot a_n^{(0)} = 0
This equation states that the zeroth correction is simply the unperturbed Hamiltonian \mathbf{H}_0, as in the case for the time independent perturbation theory.
For the first order in \lambda, we have:
\begin{aligned} & i\hbar\dot a_n^{(1)} e^{-\frac{iE_n}{\hbar}t} = \sum_j a_j^{(0)}e^{-\frac{iE_jt}{\hbar}t} \langle \psi_n |\mathbf H_p(t) | \psi_j \rangle \\ & \dot a_n^{(1)} = \frac{1}{i\hbar} \sum_j a_j^{(0)}e^{i\omega_{nj}t} \langle \psi_n | \mathbf H_p(t) | \psi_j \rangle \end{aligned}
where:
\omega_{nj} \equiv \frac{E_n - E_jt}{\hbar}
a_j^{(0)} are just constants, so knowing the state at the time t=0 and the solution of the unperturbed problem, it will be possible to integrate it and compute the first order time dependent correction as function of time; integrating:
\dot a_n^{(1)}= \frac{1}{i\hbar} \sum_j a_j^{(0)}e^{i\omega_{nj}} \langle \psi_n | \mathbf H_p(t) | \psi_j \rangle
the approximated coefficient will be:
a_n \simeq a_n^{(0)} + a_n^{(1)}(t)
and from these the wavefunction can be computed together with the behavior of the system. For higher order, the analysis will be similar and for the m^{th} order will be:
\dot a_n^{(m+1)} = \frac{1}{i\hbar} \sum_j a_j^{(m)}e^{i\omega_{nj}t} \langle \psi_n | \mathbf H_p(t) | \psi_j \rangle
So this theory is also a method of successive approximations.
Oscillating perturbations
A example, it is possible to choose monochromatic wave and express it the cosinusoidal time variation as the sum of two complex exponentials, a method which simplifies component separation. An amplitude E_0 multiplier precedes the expression. \omega > 0 signifying positive angular frequency:
E(t) = E_0\left(e^{-i\omega t} + e^{i\omega t}\right) = 2E_0\cos(\omega t)
We analyze this scenario using first-order time-dependent perturbation theory.
In this setup, we consider the field’s effect on an electron, providing the electron with electrostatic energy relative to a reference position at x= 0, Thus, the perturbing Hamiltonian \mathbf H_p(t) is:
\mathbf H_p(t) = e\, E(t)x = e\,E_0x\left(e^{-i\omega t} + e^{i\omega t}\right) = \mathbf H_{p0}\left(e^{-i\omega t} + e^{i\omega t}\right)
where e is the electronic charge, E(t) is the electric field, and x is the position;
\mathbf H_{p0} = e\,E_0x
is a part of the Hamiltonian which is independent of time. This representation of the perturbing Hamiltonian is commonly referred to as the electric dipole approximation. For the purposes of this problem, we assume that H_p(t) is activated only for a finite period, starting at t = 0 and concluding at t = t_0:
\mathbf H_p = \begin{cases} 0 & t < 0 \\ \mathbf H_{p0}\left(e^{-i\omega t} + e^{i\omega t}\right) & 0 < t < t_0 \\ 0 & t > t_0 \end{cases}
Also, for t < 0 we assume to be in an energy eigenstate |\psi_m \rangle, so the time-dependent perturbation theory will give the probability that the system will transition in another state; with this specific choice:
a_j^{(0)} = \delta_{jm}
and therefore:
\dot a_n^{(1)} = \frac{1}{i\hbar} \sum_j a_j^{(0)}e^{i\omega_{nj}t} \langle \psi_n | \mathbf H_p(t) | \psi_j \rangle = \frac{1}{i\hbar} e^{i\omega_{nm}t} \langle \psi_n | \mathbf H_p(t) | \psi_m \rangle
Using the perturbing Hamiltonian and integrating over time:
\begin{aligned} a_n^{(1)} = & \int_0^{t_0} \frac{1}{i\hbar} e^{i\omega_{nm}t} \langle \psi_n | \mathbf H_p(t) | \psi_m \rangle \mathrm dt \\ = & \frac{1}{i\hbar}\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle \int_0^{t_0} e^{i\omega_{nm}t}\left(e^{-i\omega t} + e^{i\omega t}\right) \mathrm dt \\ = & \frac{1}{i\hbar}\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle \int_0^{t_0} e^{i(\omega_{nm}-\omega) t} + e^{i(\omega_{nm} + \omega) t} \mathrm dt \end{aligned}
So for t > t_0:
\begin{aligned} a_n^{(1)} = & -\frac{1}{\hbar}\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle \left[\frac{e^{i(\omega_{nm}-\omega) t_0} - 1}{\omega_{nm}-\omega} + \frac{e^{i(\omega_{nm} + \omega) t_0} - 1}{\omega_{nm} - \omega} \right] \\ = & \frac{t_0}{i\hbar}\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle \left[e^{\frac{i(\omega_{nm}-\omega) t_0}{2}}\frac{\sin\left(\frac{(\omega_{nm}-\omega) t_0}{2} \right)}{\frac{(\omega_{nm}-\omega) t_0}{2}} + e^{\frac{i(\omega_{nm}+\omega) t_0}{2}}\frac{\sin\left(\frac{(\omega_{nm}+\omega) t_0}{2} \right)}{\frac{(\omega_{nm}+\omega) t_0}{2}} \right] \end{aligned}
The two term are the function:
\operatorname{sinc}(x) = \frac{\sin(x)}{x}
The function start at 1 for x=0 quickly approaches zero as x increases or decreases from zero, with its first zeros occurring at x=\pm \pi and the oscillations decrease in amplitude as x moves away from zero.

With this form, it means that the equation is resonant along a frequency which module is close to the frequency \omega_{nm} corresponding to the difference between the energy level n and the starting energy level m.
So the time evolution for t > t_0 at first order is:
| \Psi \rangle \approx e^{-\frac{iE_jt}{\hbar}} | \psi_m \rangle + \sum_j a_j^{(1)}(t)e^{-\frac{iE_jt}{\hbar}}| \psi_j \rangle
Now that the wavefunction has been calculated, it is possible to compute the probability that the system is found in a different state, and the probability is simply the square of the expansion coefficients:
P(n) = |a_n^{(1)}|^2
As the coefficients were calculated:
P(n) \approx \frac{t_0^2}{\hbar^2}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 \left\{\left[\frac{\sin\left(\frac{(\omega_{nm}-\omega) t_0}{2} \right)}{\frac{(\omega_{nm}-\omega) t_0}{2}} \right]^2 + \left[ \frac{\sin\left(\frac{(\omega_{nm}+\omega) t_0}{2} \right)}{\frac{(\omega_{nm}+\omega) t_0}{2}} \right]^2 + 2\cos(\omega t_0) \frac{\sin\left(\frac{(\omega_{nm}-\omega) t_0}{2} \right)}{\frac{(\omega_{nm}-\omega) t_0}{2}}\frac{\sin\left(\frac{(\omega_{nm}+\omega) t_0}{2} \right)}{\frac{(\omega_{nm}+\omega) t_0}{2}} \right\}
This term:
2\cos(\omega t_0) \frac{\sin\left(\frac{(\omega_{nm}-\omega) t_0}{2} \right)}{\frac{(\omega_{nm}-\omega) t_0}{2}}\frac{\sin\left(\frac{(\omega_{nm}+\omega) t_0}{2} \right)}{\frac{(\omega_{nm}+\omega) t_0}{2}}
will be zero if the perturbation has been ongoing for some time because even if one of the two term is large, the other will be small, and therefore the probability remaining is:
P(n) \approx \frac{t_0^2}{\hbar^2}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 \left\{\left[\frac{\sin\left(\frac{(\omega_{nm}-\omega) t_0}{2} \right)}{\frac{(\omega_{nm}-\omega) t_0}{2}} \right]^2 + \left[ \frac{\sin\left(\frac{(\omega_{nm}+\omega) t_0}{2} \right)}{\frac{(\omega_{nm}+\omega) t_0}{2}} \right]^2 \right\}
This transition probability is influenced by the square of the perturbation strength and the squared modulus of the perturbation matrix element. Specifically, we compute the modulus squared of the matrix element between the initial and final states mediated by the time-independent component of the perturbing Hamiltonian, \mathbf H_{p0}.
In the scenario where an oscillating electric field influences an electron, the transition probability is directly proportional to the square of the field’s amplitude, encapsulated within \mathbf H_{p0}. Consequently, this squared amplitude is indicative of the transition’s likelihood. Furthermore, in the context of electromagnetism, the intensity of a light field, defined as the power per unit area, is proportional to the square of the electric field amplitude. Thus, the likelihood of transitioning from state m to state n scales with the intensity of the electromagnetic field acting upon the system.
The first term becomes relevant when \omega_{nm}, the frequency difference between the states, is approximately equal to \omega. This condition corresponds to the situation where the energy \hbar \omega matches E_n - E_m. Given that \omega is positive, this term is significant in scenarios involving energy absorption, where the system transitions from a lower energy state m to a higher energy state n.
Conversely, the second term gains significance when -\omega_{nm} approximates \omega, effectively rendering the expression close to zero. This occurs when \hbar \omega is approximately equal to E_m - E_n, implying that E_n is lower than E_m. As \omega is positive, this condition aligns with energy emission, where the system transitions from a higher energy state m to a lower energy state n.
Fermi’s golden rule
Suppose we are dealing with not just a single specific transition energy \hbar \omega_{nm}, but a dense spectrum of possible transitions around a given photon energy \hbar \omega. In such scenarios, especially in solid materials, individual atoms or particles may exhibit slightly varying transition energies due to their unique electronic structures. Despite these variations, these transitions might share approximately the same matrix elements, suggesting uniform transition strengths if matched with the correct frequency.
In this context, we describe the collection of potential transition energies as being densely packed in terms of frequency or energy. This concept leads to defining a density of states specific to these transitions, denoted as g_N(\hbar \omega). This density represents the number of transitions per unit energy around the photon energy \hbar \omega.
When considering a small energy range, \Delta E, around \hbar \omega, the total number of possible transitions within this range is given by the product g_N(\hbar \omega) \times \Delta E. Here, g_N(\hbar \omega) is termed the joint density of states, reflecting the density of transition energies rather than merely the density of specific energy states.
This framework allows for the summation of the probabilities of absorption for all these closely spaced transitions, leading to a total probability of absorption for this band of energies. Thus, in materials with a dense set of possible transitions, the likelihood of photon absorption increases with the density of these available states:
P_{tot} \approx \frac{t_0^2}{\hbar^2}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 \int \left[\frac{\sin\left(\frac{(\omega_{nm}-\omega) t_0}{2} \right)}{\frac{(\omega_{nm}-\omega) t_0}{2}} \right]^2 g_N(\hbar \omega_{nm}) \mathrm d (\hbar \omega_{nm})
Over small energies range, g_N(\hbar \omega_{nm}) is approximately constant and can be taken out as g_N(\hbar \omega) :
P_{tot} \approx \frac{t_0^2}{\hbar^2}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 g_N(\hbar \omega) \int \left[\frac{\sin\left(\frac{(\omega_{nm}-\omega) t_0}{2} \right)}{\frac{(\omega_{nm}-\omega) t_0}{2}} \right]^2 \mathrm d (\hbar \omega_{nm})
changing the variable:
x = \frac{(\omega_{nm}-\omega) t_0}{2}
the integral becomes:
P_{tot} \approx \frac{t_0^2}{\hbar^2}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 \frac{2\hbar}{t_0} g_N(\hbar \omega) \int \left[\frac{\sin\left(x\right)}{x} \right]^2 \mathrm d x
as:
\int \left[\frac{\sin\left(x\right)}{x} \right]^2 \mathrm d x = \pi
the final result is:
P_{tot} \approx \frac{2\pi t_0}{\hbar}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 g_N(\hbar \omega)
The probability of transition it is proportional to the time for which the perturbation has been applied. And so therefore, we can deduce a transition rate:
W = \frac{P_{tot}}{t_0} = \frac{2\pi}{\hbar}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 g_N(\hbar \omega)
This is known as Fermi’s Golden Rule.
Using the Dirac Delta, it can be rewritten as:
w_{nm} = \frac{2\pi}{\hbar}\left|\langle \psi_n | \mathbf H_{p0} | \psi_m \rangle\right|^2 \delta(E_{nm} - \hbar \omega)
where w_{nm} is the transition rate and therefore the total transition rate in the neighborhood is then:
W = \int w_{nm}g_j(\hbar \omega_{nm}) \mathrm d(\hbar \omega_{nm})