Infinite Potential well with an electric field
Considering an electron in a potential field with infinitely high walls and then we will apply an electric field with magnitude, \mathbf E, pointing in a specific direction. This will result in a potential energy difference across the well of eE\cdot L, where e is the electronic charge, E is the electric field, and L is the thickness. As one moves from one side of the well to the other, an electron’s energy increases by this amount.
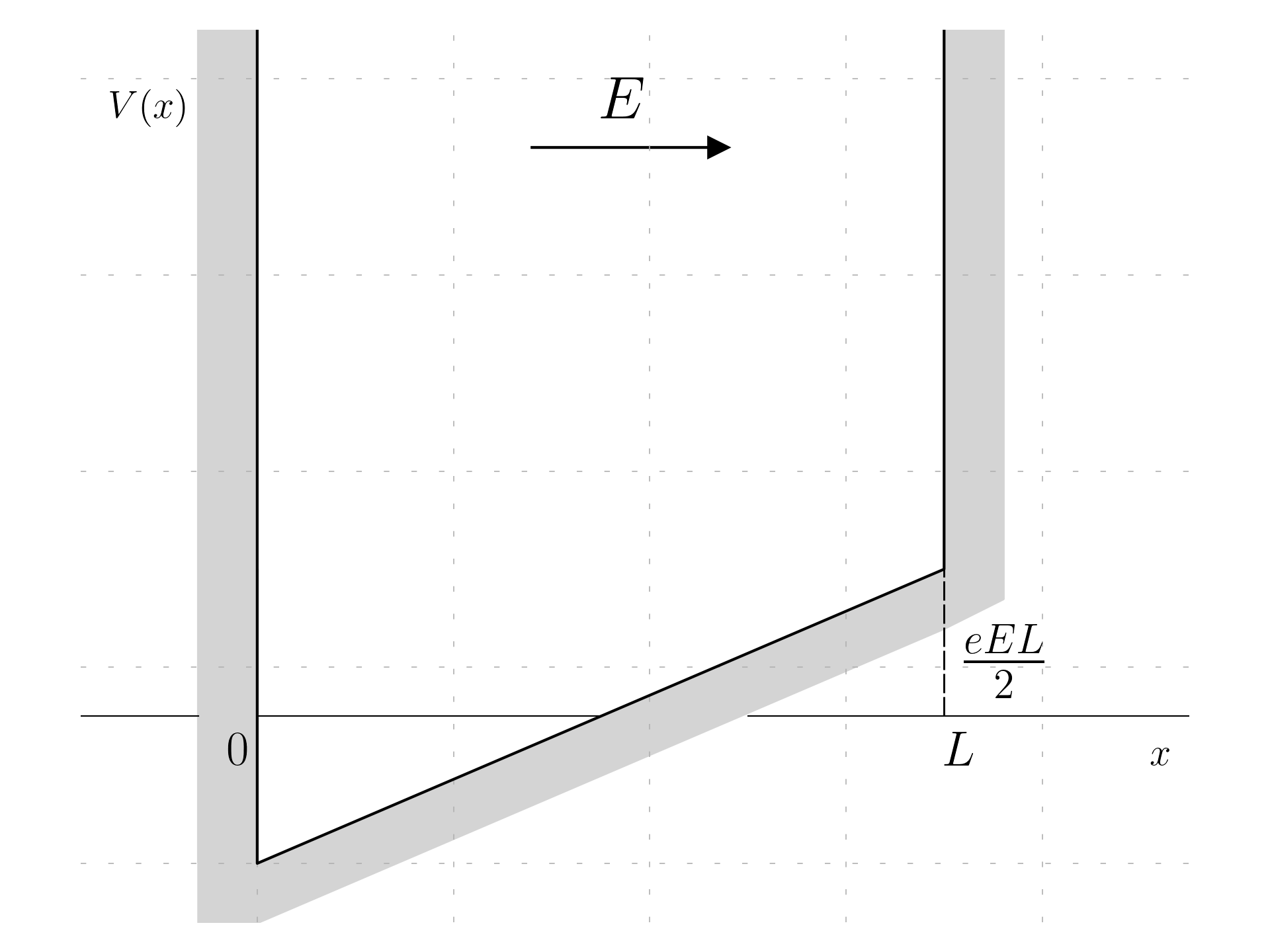
In essence, the energy of an electron in an electric field, E, increases linearly with its position. A positive electric field in the positive x direction exerts a force on the electron towards the negative x direction.
The potential energy of an electron in a field directed in the positive x direction grows as one moves in the positive x direction, due to the force pushing in the opposite direction. This potential energy, as a function of position x, is eEx, where e is the electronic charge, E is the field, and x is the distance.
For this scenario, we set the potential energy to be zero at the well’s midpoint. Therefore, within the well, the potential energy is eEx, with x denoting the position relative to the well’s center. This means at x = \frac{L}{2}, the midpoint of the well, the potential energy is zero.
The potential energy is then:
V(x) = \begin{cases} eE\left(x-\frac{L}{2}\right) & \quad 0 \le x \le L \\ \infty & \quad x < 0, x > L\end{cases}
The Hamiltonian becomes:
\mathbf H = -\frac{\hbar^2}{2m}\frac{\mathrm d^2}{\mathrm dx^2} + V(x) = -\frac{\hbar^2}{2m}\frac{\mathrm d^2}{\mathrm dx^2} + eE\left(x-\frac{L}{2}\right)
It is possible to scale this equation to dimensionless unit, using as reference for the energy the confinement of the first state of the infinitely deep well:
E_1^\infty = \frac{\hbar^2}{2m}\left(\frac{\pi}{L}\right)^2
Then the dimensionless eigenenergy for the state n will be:
\eta_n = \frac{E_n}{E_1^\infty}
For an unit of field E_0, a possible choice is one that would give one energy unit of potential change from one side of the well to the other:
E_0 = \frac{E_1^\infty}{eL}
The dimensionless field is then f, which is the actual field divided by this field:
f = \frac{E}{E_0} = \frac{EeL}{E_1^\infty}
Finally a convenient distance unit in this problem is naturally the thickness of the well L, so the dimensionless distance will be:
\xi = \frac{x}{L}
Using these in the original Hamiltonian dividing by E_1^\infty:
\mathbf H =\frac{1}{E_1^\infty}\left[ -\frac{\hbar^2}{2m}\frac{\mathrm d^2}{\mathrm dx^2} + eE\left(x-\frac{L}{2}\right)\right] = -\frac{1}{\pi^2}L^2\frac{\mathrm d^2}{\mathrm dx^2} + fL\left(x-\frac{L}{2}\right)
in dimensionless units:
\mathbf H = -\frac{1}{\pi^2}\frac{\mathrm d^2}{\mathrm d\xi^2} + f\left(\xi-\frac{1}{2}\right)
So the Schrödinger equation is:
\mathbf H\phi(\xi) = \epsilon \phi(\xi)
In the unperturbed state, the Hamiltonian is:
\mathbf H_0 = -\frac{1}{\pi^2}\frac{\mathrm d^2}{\mathrm d\xi^2}
and the solution for the Schrödinger equation:
\mathbf H_0\psi_n = \varepsilon_n \psi_n
are wavefunctions:
\psi_n(\xi) = \sqrt 2 \sin\left(n\pi\xi\right)
For the perturbed state, the objection is arrive at a form where it is possible use the Airy functions (which are the known solution for this problem), it is then necessary to transform the Schrödinger equation into the form of the Airy differential equation. This can be done by introducing a new variable and performing a suitable change of variables.
-\frac{1}{\pi^2}\frac{\mathrm d^2\phi}{\mathrm d\xi^2} + f\left(\xi-\frac{1}{2}\right)\phi(\xi) = \eta \phi(\xi) \frac{1}{\pi^2}\frac{\mathrm d^2\phi}{\mathrm d\xi^2} - f\left(\xi-\frac{1}{2}\right)\phi(\xi) + \eta \phi(\xi) =0
Rewriting the Schrödinger equation as:
\frac{\mathrm{d}^2\phi(\xi)}{\mathrm{d}\xi^2} - \pi^2\left[f\left(\xi - \frac{1}{2}\right) - \eta \right]\phi(\xi) =\frac{\mathrm{d}^2\phi(\xi)}{\mathrm{d}\xi^2} - \left[ f\pi^2\xi - \pi^2\eta - \frac{f\pi^2}{2} \right]\phi(\xi) = 0
Introducing a new variable \alpha defined as:
\alpha \equiv {\left(f\pi^2\right)}^{1/3}\xi, \quad \xi = {\left(f\pi^2\right)}^{-1/3}\alpha
Expressing the wavefunction \phi(\xi) in terms of the new variable \alpha:
\phi(\xi) = \phi\left(\left(f\pi^2\right)^{-2/3}\alpha\right) \equiv \phi(\alpha)
where \phi(\alpha) is a new function of \alpha.
Substituting this into the Schrödinger equation and apply the chain rule and the derivative \frac{d\alpha}{d\xi} = {\left(f\pi^2\right)}^{1/3}:
\begin{aligned} & \frac{d^2\phi}{d\alpha^2}\left(\frac{d\alpha}{d\xi}\right)^2 - \left[ f\pi^2\left(f\pi^2\right)^{-1/3}\alpha - \pi^2\eta - \frac{f\pi^2}{2} \right]\phi(\alpha) = 0 \\ & \frac{d^2\phi}{d\alpha^2}{\left(f\pi^2\right)}^{2/3} - \left[\left(f\pi^2\right)^{2/3}\alpha - \pi^2\eta - \frac{f\pi^2}{2} \right]\phi(\xi) = 0 \\ & \frac{d^2\phi}{d\alpha^2} - \left[\frac{\left(f\pi^2\right)^{2/3}}{{\left(f\pi^2\right)}^{2/3}}\alpha - \frac{\pi^2\eta + \frac{f\pi^2}{2}}{{\left(f\pi^2\right)}^{2/3}} \right]\phi(\alpha) = 0 \\ & \frac{d^2\phi}{d\alpha^2} - \left[\alpha - {\left(f\pi^2\right)}^{-2/3}\left(\pi^2\eta + \frac{f\pi^2}{2}\right) \right]\phi(\alpha) = 0 \\ & \frac{d^2\phi}{d\alpha^2} - \left[\alpha - \alpha_c \right]\phi(\alpha) = 0 \end{aligned}
where:
a_c = {\left(f\pi^2\right)}^{-2/3}\left(\pi^2\eta + \frac{f\pi^2}{2}\right) = {\left(f\pi^2\right)}^{-2/3}\pi^2 \left(\eta + \frac{f}{2}\right) = \left(\frac{\pi}{f}\right)^{2/3}\left(\eta + \frac{f}{2}\right)
This is the Airy differential equation, and its solutions are the Airy functions, \mathrm{Ai}(z) and \mathrm{Bi}(z). The solutions to the original Schrödinger equation can be written as:
\phi(\alpha) = C_1\mathrm{Ai}\left[\alpha - \alpha_c\right] + C_2\mathrm{Bi}\left[\alpha - \alpha_c\right]
where C_1 and C_2 are arbitrary constants determined by the boundary conditions.
For an infinite potential well with boundaries the condition for x(0)=x(L)=0 or \alpha(0) = \alpha(1)=0, the boundary conditions are:
\begin{aligned} & \phi(0) = 0 \\ & \phi(1) = 0 \end{aligned}
Defining
\begin{aligned} & \alpha_0 = -\alpha_c= -\left(\frac{\pi}{f}\right)^{2/3}\left(\eta + \frac{f}{2}\right) \\ & \alpha_L = {\left(f\pi^2\right)}^{1/3} - \alpha_c = {\left(f\pi^2\right)}^{1/3} -\left(\frac{\pi}{f}\right)^{2/3}\left(\eta + \frac{f}{2}\right) \end{aligned}
and apply the boundary conditions:
\begin{aligned} & C_1\mathrm{Ai}\left(\alpha_0\right) + C_2 \mathrm{Bi}\left(\alpha_0\right) = 0 \\ & C_1\mathrm{Ai}\left(\alpha_L\right) + C_2 \mathrm{Bi}\left(\alpha_L\right) = 0 \end{aligned}
In matrix form:
\begin{bmatrix} \mathrm{Ai}\left(\alpha_0\right) & \mathrm{Bi}\left(\alpha_0\right) \\ \mathrm{Ai}\left(\alpha_L\right) & \mathrm{Bi}\left(\alpha_L\right) \end{bmatrix} \begin{bmatrix}C_1 \\ C_2 \end{bmatrix} = \begin{bmatrix}0 \\ 0 \end{bmatrix}
So the determinant of the matrix must be zero:
\mathrm{Ai}\left(\alpha_0\right) \mathrm{Bi}\left(\alpha_L\right) - \mathrm{Ai}\left(\alpha_L\right) \mathrm{Bi}\left(\alpha_0\right) = 0
These equations cannot be solved analytically for \eta in general, but can be solved them numerically to find the allowed values of \eta_n that satisfy the boundary conditions; once these allowed energy eigenvalues are found, it is possible determine the corresponding constants C_1 and C_2 to obtain the normalized wave function \phi_n(\alpha), or \phi_n(\xi) or \phi_n(x); any can be normalized on a suitable interval.
Constant electric field example
Considering a constant electric field f_0 = 3, the first step is to compute the roots of the determinant.
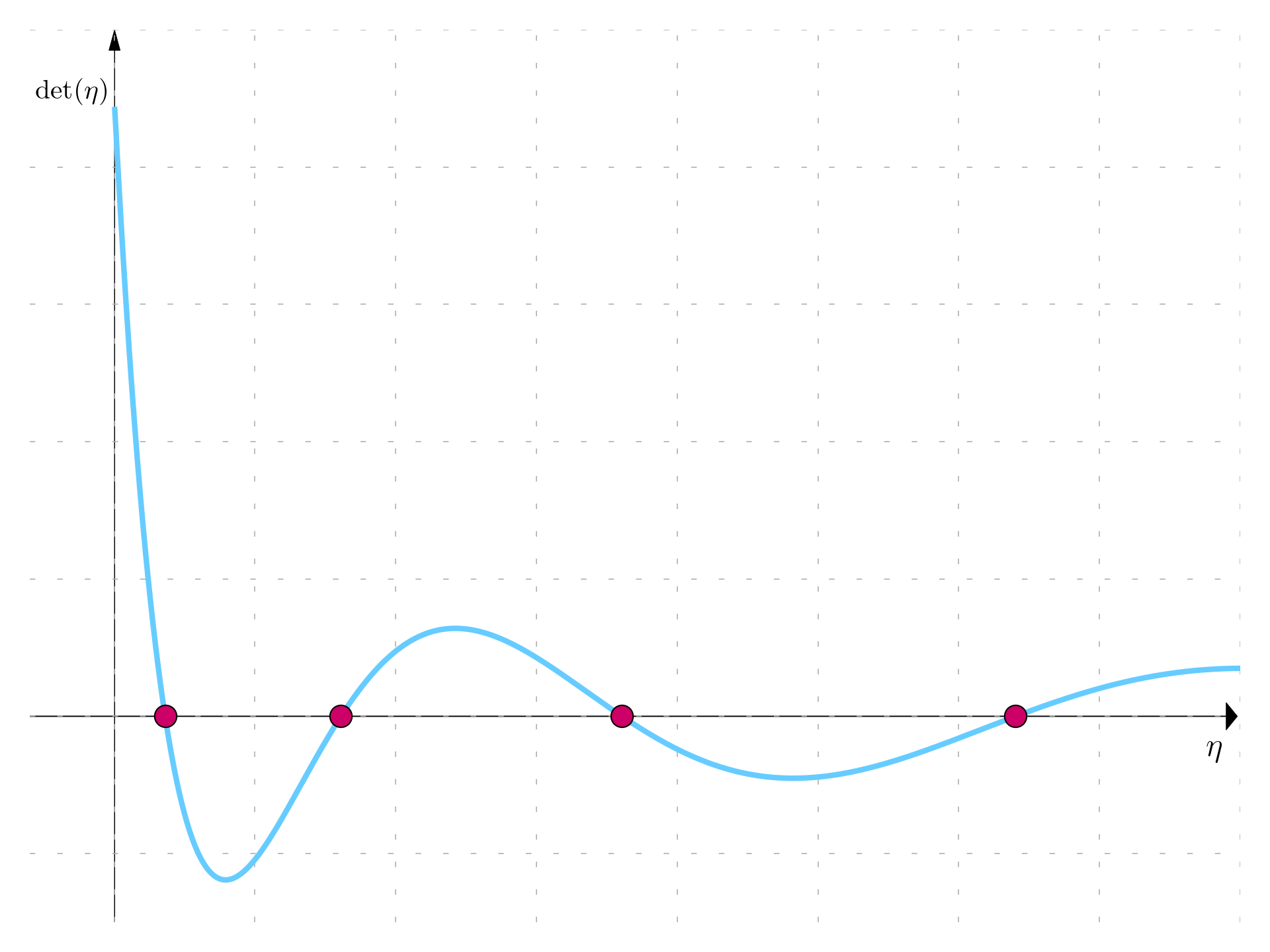
Using a numerical method, in the range [0,20], 4 levels of energy are identified:
\begin{aligned} & \eta_1 = 0.90419 \\ & \eta_2 = 4.02746 \\ & \eta_3 = 9.01726 \\ & \eta_4 = 16.0106 \end{aligned} These are quite close to the correspondent \varepsilon_i energies (1, 4, 9, and 16 respectively); noting that the first eigenvalue is slightly below while the remaining are slightly above.
The ratio between the constants can be computed from:
\begin{aligned} & C_1\mathrm{Ai}\left(\alpha_0\right) + C_2 \mathrm{Bi}\left(\alpha_0\right) = 0 \\ & \frac{C_1}{C_2} = -\frac{\mathrm{Bi}\left(\alpha_0\right)}{\mathrm{Ai}\left(\alpha_0\right)} \end{aligned}
For the specific problem the ratio for \eta_i is:
\begin{aligned} & \text{ratio}_1 = -4.44828 \\ & \text{ratio}_2 = -2.20666 \\ & \text{ratio}_3 = 1.67391 \\ & \text{ratio}_4 = 0.10324 \end{aligned}
Now it is possible to normalize the wavefunction:
\phi(\alpha) = C_1\mathrm{Ai}\left[\alpha - \alpha_c\right] + C_2\mathrm{Bi}\left[\alpha - \alpha_c\right]
In the \xi units and setting C_2=1:
\int_0^1 |\phi_n(\xi)|^2 \mathrm d\xi = \int_0^1 \left(\text{ratio}_{n}\mathrm{Ai}\left[{\left(f\pi^2\right)}^{1/3}\xi - \alpha_c\right] + \mathrm{Bi}\left[{\left(f\pi^2\right)}^{1/3}\xi - \alpha_c\right]\right)^2\mathrm d\xi = 1
Solving numerically, the constants are:
\begin{array}{|c|c|} \hline C_1 & C_2 \\ \hline 2.74241 & -0.61651 \\ 3.25156 & -1.47352 \\ 3.75309 & -2.242101 \\ 0.51864 & 5.02374 \\ \hline \end{array}
The sign of these constants has been chosen to approximate the shape of the exact solution for visualization purposes (since the normalization constant is a factor |A^2| both \pm A are valid normalization factor) and the probability density depends from the square of the wavefunction anyway.
It is possible to plot these wavefunctions (in blue) and compare them with the unperturbed state (in orange).
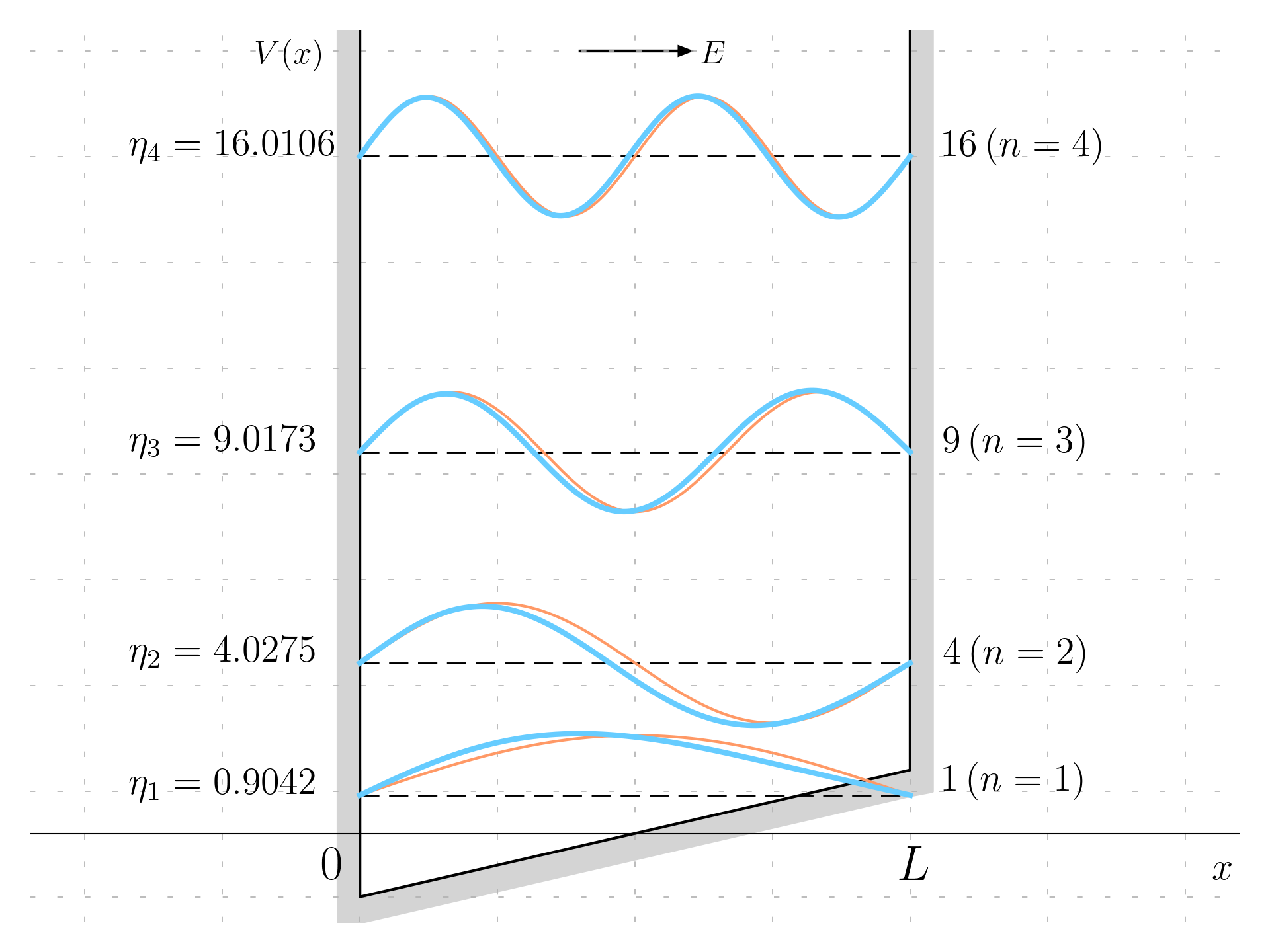
These wavefunctions go to zero on both side of the well, and are sufficiently close to the solutions of the undisturbed infinite potential well, but with a shift to the left due to the presence of the electric field; this is evident when looking at the graph and the probability density and compare it with the one of the exact solution.
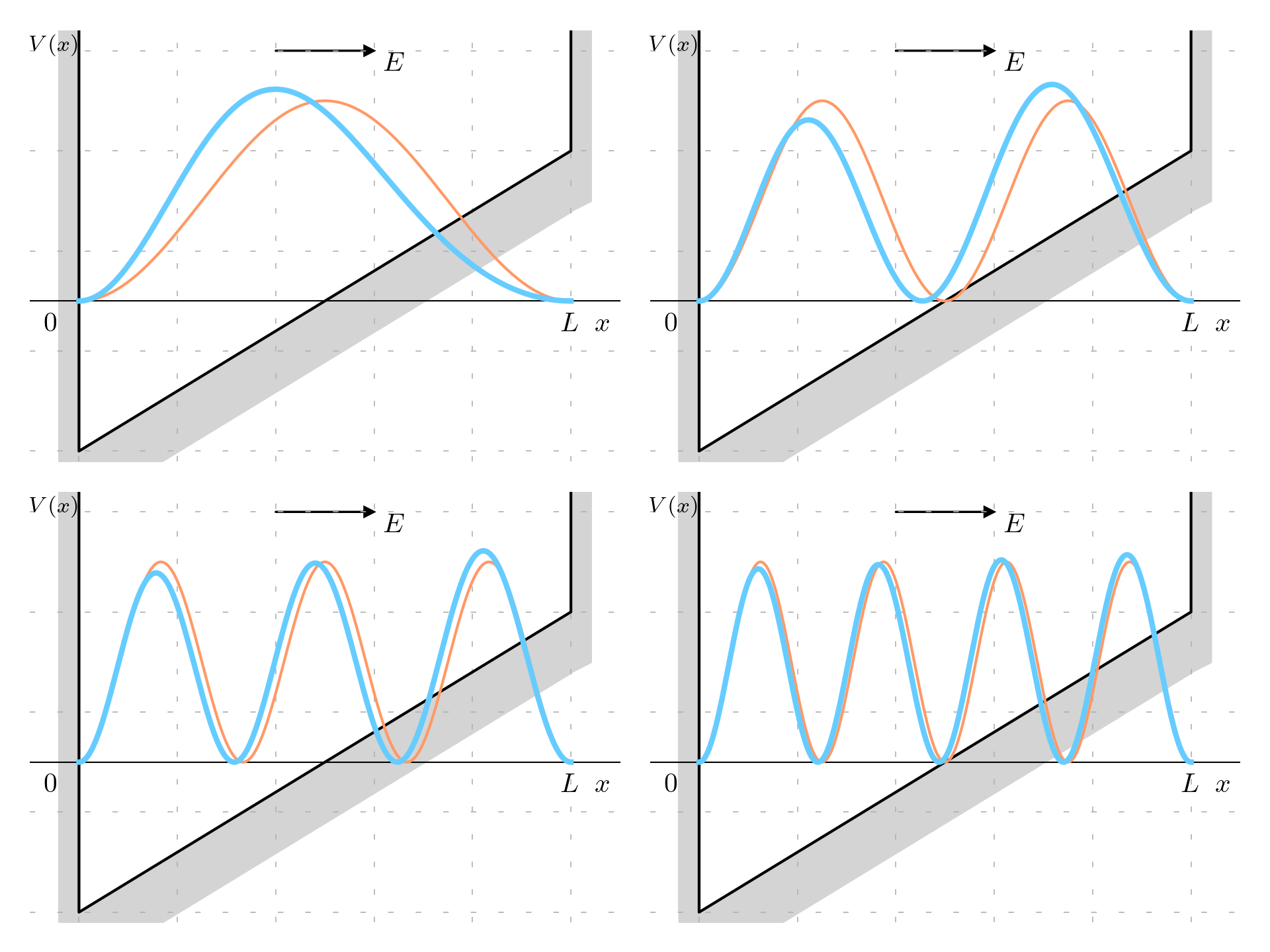
When increasing the energy, the effect of the electric field is diminishing and the probability density is getting closer the the ones of the undisturbed infinite potential well probability density.