Finite Matrices
Finite matrix approximation in quantum mechanics is a numerical method used to approximate solutions to quantum mechanical problems that involve operators on infinite-dimensional spaces, such as the Hamiltonian operator. This method is particularly useful in scenarios where exact solutions are difficult or impossible to obtain analytically.
The core concept of finite matrix approximation is to discretize the problem by projecting the infinite-dimensional operators into a finite-dimensional subspace. This is achieved by selecting a suitable basis set, such as wavefunctions or orthogonal polynomials, and limiting the space to the first N basis functions. The infinite-dimensional operator, typically the Hamiltonian, is then represented as a finite matrix within this truncated basis.
By doing this, the problem of solving the Schrödinger equation transforms into a matrix eigenvalue problem. The matrix derived from the Hamiltonian in the finite basis set is diagonalized to obtain eigenvalues and eigenvectors. The eigenvalues approximate the energy levels of the quantum system, while the eigenvectors correspond to the approximate wavefunctions.
The accuracy of the finite matrix approximation depends on the size of the matrix (i.e., the number of basis functions used) and the choice of the basis set. A larger matrix typically provides better approximations but requires more computational resources. The choice of basis set is crucial as it should reflect the properties of the physical system to minimize the truncation errors.
Applications of finite matrix approximation are widespread in quantum mechanics, particularly in quantum chemistry and solid-state physics, where it is used to calculate molecular energy levels, electron configurations, and other properties of complex systems. The method is also pivotal in numerical studies involving quantum dots, quantum wells, and nanoparticles where traditional analytical solutions are unfeasible.
Overall, finite matrix approximation is a powerful tool in theoretical and computational physics, providing a practical approach to solving high-dimensional quantum mechanical problems by leveraging modern computational techniques.
Example - infinite potential well with electric field
Using energy eigenfunctions from an unperturbed or simpler related problem as a starting basis set is a common technique and, as example, it is possible to approximate the behavior of an electron in an infinite well with an applied electric field (for which an analytic solution has been derived here).
As a first step, it is necessary to choose the basis and for the specific case will be the unperturbed problem (particle in a box), For an electron in a one-dimensional infinite potential well, the energy eigenfunctions \phi_n(x) are given by:
\phi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi x}{L}\right)
where n is a positive integer, and L is the length of the box. These functions are solutions to the time-independent Schrödinger equation without an external field.
In an dimensionless format are:
\phi_n(\xi) = \sqrt 2 \sin\left(n\pi\xi\right)
As a second step, it is necessary to construct the Hamiltonian matrix; when an electric field E is applied along the box, the potential energy term in the Hamiltonian can be represented as V(x) = -eEx, where e is the electron charge. The total Hamiltonian H is then:
\mathbf H = -\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} - eEx
In dimensionless format is:
\mathbf H = -\frac{1}{\pi^2}\frac{\mathrm d^2}{\mathrm d\xi^2} + f\left(\xi-\frac{1}{2}\right)
Using the eigenfunctions of the unperturbed problem, we can construct the matrix elements of the Hamiltonian as:
\mathbf H_{ij} = \langle \bar \phi_i | H | \phi_j \rangle
which includes both the kinetic term and the potential term due to the electric field:
H_{ij} = \int_0^1 \bar \phi_i(\xi) \left(-\frac{1}{\pi^2} \frac{\mathrm{d}^2}{\mathrm{d}\xi^2}\right) \phi_j(\xi) \, \mathrm{d}\xi + \int_0^1 \phi_i(\xi) \left(f \left(\xi - \frac{1}{2}\right)\right) \phi_j(\xi) \, \mathrm{d}\xi
Expanding in the unperturbed problem eigenfunction as basis:
\begin{aligned} H_{ij} & = -\frac{-2j^2\pi^2}{\pi^2} \int_0^1 \sin\left(i\pi\xi\right) \sin\left(j\pi\xi\right) \, \mathrm{d}\xi + 2f \int_0^1 \sin\left(i\pi\xi\right)\left(\xi - \frac{1}{2}\right) \sin\left(j\pi\xi\right) \, \mathrm{d}\xi \\ & = 2j^2 \int_0^1 \sin\left(i\pi\xi\right) \sin\left(j\pi\xi\right) \, \mathrm{d}\xi + 2f \int_0^1 \left(\xi - \frac{1}{2}\right)\sin\left(i\pi\xi\right)\sin\left(j\pi\xi\right) \, \mathrm{d}\xi \end{aligned}
The first integral is straightforward:
2j^2\frac{1}{2}\delta_{ij} = i^2\delta_{ij}
To derive the result for the second integral integral (it will be multiplied by 2f at the end):
I = \int_0^1 \left(\xi - \frac{1}{2}\right)\sin(i\pi\xi)\sin(j\pi\xi) \, \mathrm{d}\xi
it can be split in two cases, with i = j, we have:
I = \int_0^1 \left(\xi - \frac{1}{2}\right)\sin^2(i\pi\xi) \, \mathrm{d}\xi
Using the trigonometric identity \sin^2(x) = \frac{1}{2}(1 - \cos(2x)), we get:
\begin{aligned} I &= \frac{1}{2}\int_0^1 \left(\xi - \frac{1}{2}\right) \, \mathrm{d}\xi - \frac{1}{2}\int_0^1 \left(\xi - \frac{1}{2}\right)\cos(2i\pi\xi) \, \mathrm{d}\xi \\ &= \frac{1}{2}\left[\frac{1}{2}\xi - \frac{1}{4}\xi^2\right]_0^1 - \frac{1}{4i\pi}\int_0^{2i\pi} \left(\frac{u}{2i\pi} - \frac{1}{2}\right)\cos(u) \, \mathrm{d}u \\ &= \frac{1}{8} - \frac{1}{8} \\ &= 0 \end{aligned}
For the second set of case with i \neq j the solution is complex but analytical:
I_a = \frac{-4ij + \sin(i\pi)\left((i-j)j(i+j)\pi\cos(j\pi) + 2(i^2 + j^2)\sin(j\pi)\right) + i\cos(i\pi)\left(4j\cos(j\pi) + (-i+j)(i+j)\pi\sin(j\pi)\right)}{2(i^2 - j^2)^2\pi^2}
Combining all together the Hamiltonian matrix is:
H_{ij}= \begin{cases} i^2 & i = j \\[12pt] 2fI_a & i \neq j \end{cases}
For example, with n=4, the resulting Hamiltonian is:
\mathbf H = \begin{bmatrix} 1 & -0.5404 & 0 & -0.0432 \\ -0.5404 & 4 & -0.5836 & 0 \\ 0 & -0.5836 & 9 & -0.5955 \\ -0.0432 & 0 & -0.5955 & 16 \end{bmatrix}
As expected, this matrix is Hermitian.
Once it is computed, the next step is to diagonalize the Hamiltonian matrix; by constructing the Hamiltonian matrix using the finite basis set \{\phi_n\} and computing these integrals, we obtain a finite matrix representation of the Hamiltonian. This matrix is then diagonalized to find the approximate energy eigenvalues and the corresponding eigenvectors of the system with the electric field.
These quantities can be found numerically; for the specific example the eigenvalues are:
\begin{array}{|c|} \hline \eta \\ \hline 0.9042 \\ 4.02763 \\ 9.01753 \\ 16.05064 \\ \hline \end{array}
These are quite close to the unperturbed Hamiltonian (which are n^2, so 1, 4, 9, 16, …). In the page here the exact solution have been computed (using the Airy functions) and the eigenenergies are:
\begin{array}{|c|} \hline \eta \\ \hline 0.90419 \\ 4.02746 \\ 9.01726 \\ 16.0106 \\ \hline \end{array}
They are very close, barely noticeable for the first three; just a bit off for the fourth but it is expected because only four basis functions are used.
The eigenvectors are:
\begin{array}{|c|c|c|c|} \hline | \phi_1 \rangle & | \phi_2 \rangle & | \phi_3 \rangle & | \phi_4 \rangle \\ \hline 0.98461 & -0.17460 & 0.00736 & -0.00301 \\ 0.17428 & 0.97784 & -0.11590 & 0.00423 \\ 0.01281 & 0.11538 & 0.98964 & -0.08451 \\ 0.00332 & 0.00511 & 0.08445 & 0.99641 \\ \hline \end{array}
These are normalized (|\phi_i|=1); it worth nothing that the biggest contribution is coming from the i^{th} of the unperturbed solution.
These eigenvectors represent the coefficients of the linear combination of your basis functions that approximate the true wavefunctions \phi of the quantum system under study. Each eigenvector obtained from diagonalizing the Hamiltonian matrix corresponds to one wavefunction of the system. An eigenvector | \phi_n \rangle = (c_1, c_2, \dots, c_N) provides the coefficients for the linear combination of the basis functions used to approximate the wavefunction.
The basis functions, \{\phi_1, \phi_2, \dots, \phi_N\}, which were initially chosen to span the space; the wavefunction \phi_n associated with the n^{th} eigenvalue can be constructed as follows:
\phi_n(x) = \sum_{k=1}^N c_{nk} \phi_k(x)
where c_{nk} are the components of the n^{th} eigenvector, and \phi_k(x) are the basis functions. This sum represents the approximation of the true wavefunction as a linear combination of a chosen basis.
It may be needed to normalize the resulting wavefunctions to ensure that they satisfy the normalization condition:
\int |\phi_n(x)|^2 \, dx = 1
For a simple case of a particle in a box using sinusoidal basis functions, if the first eigenvector is \mathbf{v}_1 = (c_{11}, c_{12}, \dots, c_{1N}), the first approximated wavefunction is:
\phi_1(x) = c_{11} \sqrt{2} \sin(\pi x) + c_{12} \sqrt{2} \sin(2\pi x) + \dots + c_{1N} \sqrt{2} \sin(N\pi x)
In the specific case, the first eigenfunction is:
\phi_1(x) = 0.98461 \sqrt{2} \sin(\pi x) + 0.17428 \sqrt{2} \sin(2\pi x) + 0.01281 \sqrt{2} \sin(3\pi x) + 0.00332 \sqrt{2} \sin(4\pi x)
And for the other there is a similar expression. These are already normalized; it was numerically checked, but also analytically can be easily proven as when computing |\phi|^2, there are term of the form \sin(n \pi x)\sin(m \pi x), which are \delta{ij} and give \frac{1}{2}, multiplied by (\sqrt 2)^2, leaving just the square of each component of the eigenvector, which is normalized as previously shown and therefore the wave function is also normalized.
It is possible to plot the probability density for the computed states for n=1,2,3,4 and compare the approximated solution (in red) with the exact solution (in blue) and with the unperturbed solution (in orange).
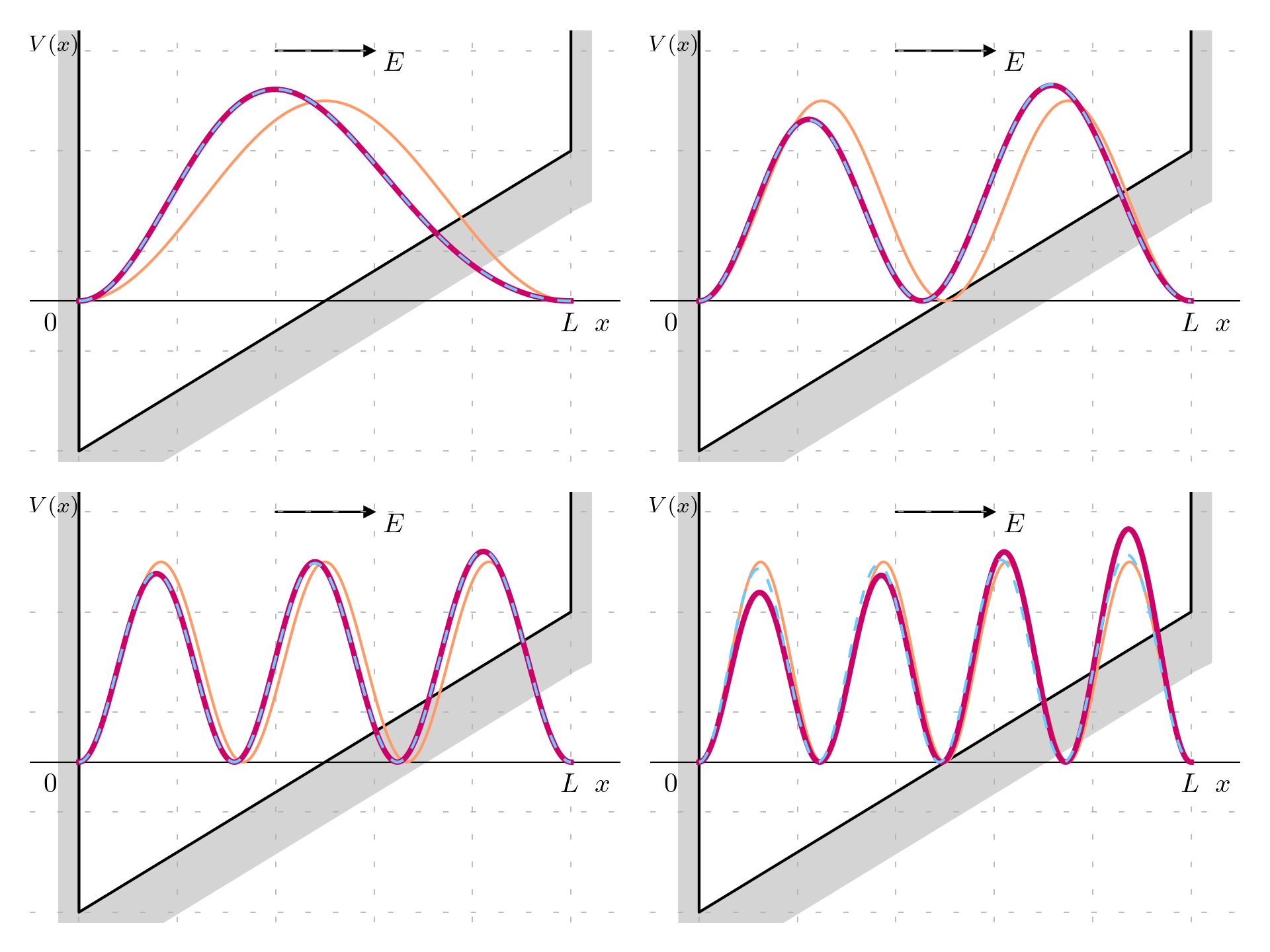
In this case it is clear (as in the exact solution) that the distribution (and therefore the wavefunction) moved to the left, as expected since the slope of the electric field is tilted to the left and therefore it would be expected that the electron move in that direction; as for the accuracy, the first three state are matching almost perfectly the analytical solution (the two curves are practically superposed), while for n=4 they start to be relatively different (the pattern is similar but the peak of the amplitude is off).
For this method, the overall the accuracy of this approximation depends on the size of the basis set used. A larger set will typically yield more accurate results but at the cost of increased computational effort. The choice of basis size and the specific eigenfunctions used can be adjusted based on the strength of the electric field and the specifics of the physical setup. By employing the finite matrix approximation with a well-chosen basis set derived from the simpler problem, one can efficiently study the effects of the electric field on the electron in the box, facilitating the exploration of quantum mechanical effects under different field strengths.