Optical Absorption in Semiconductors
Introduction
Quantum optical absorption in semiconductors is primarily governed by the interaction of light with the electronic states within the material. This phenomenon is critical in determining the optical properties of semiconductors and is exploited in various applications including photodetectors, solar cells, and light-emitting devices. The absorption process involves the excitation of electrons from the valence band to the conduction band by photons whose energy matches the bandgap of the semiconductor.
The quantum mechanical nature of this interaction is described by the electronic band structure of the material, which dictates the allowed energy states for electrons. Factors such as quantum confinement, where the dimensions of the semiconductor are on the order of the exciton Bohr radius, significantly alter the absorption spectrum. This leads to discrete energy levels and enhanced optical properties, evident in quantum wells, quantum dots, and quantum wires. The precise control over these quantum structures allows for the engineering of semiconductor devices with optimized optical characteristics.
Perturbing Hamiltonian
The transition rate for absorption from an initial state |\psi_i \rangle and an energy E_i to a final state |\psi_f \rangle and energy E_f a is given by the Fermi’s golden rule (here):
w_{if} = \frac{2\pi}{\hbar}\left|\langle \psi_f | \mathbf H_{p0} | \psi_i \rangle\right|^2 \delta(E_f - E_i - \hbar\omega)
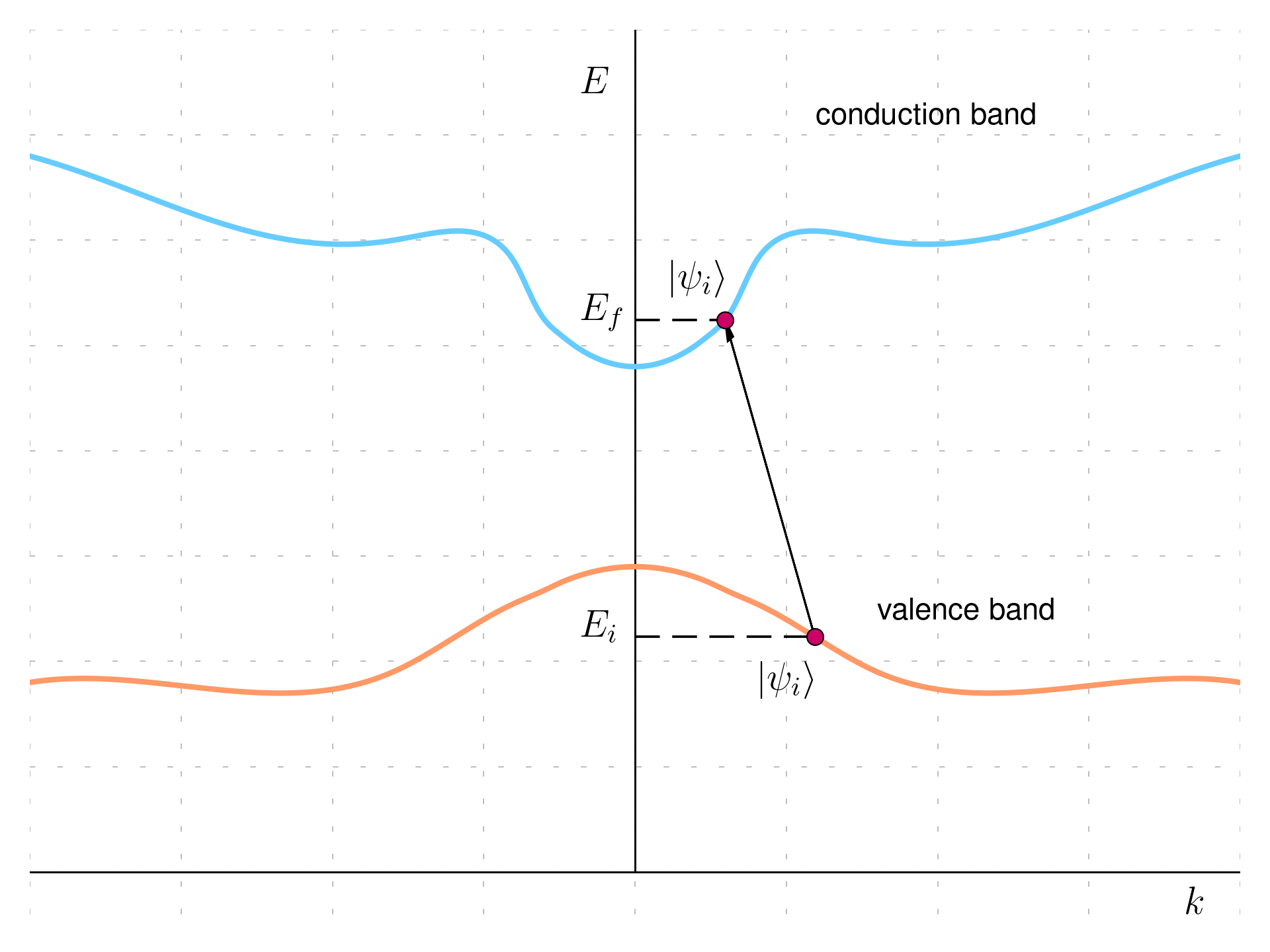
The perturbing Hamiltonian varies as an amplitude of an electromagnetic wave:
\mathbf H_p(t) = e\, E(t)x = e\,E_0x\left(e^{-i\omega t} + e^{i\omega t}\right) = \mathbf H_{p0}\left(e^{-i\omega t} + e^{i\omega t}\right)
As further assumption the perturbing Hamiltonian can vary through spatial dependence of the electromagnetic wave amplitude:
\mathbf H_p(\mathbf r, t) = \mathbf H_{p0}(\mathbf r)\left(e^{-i\omega t} + e^{i\omega t}\right)
Then explicitly:
\langle \psi_f | \mathbf H_{p0} | \psi_i \rangle = \int \bar \psi_f(\mathbf r)\mathbf H_{p0}(\mathbf r) \psi_i(\mathbf r) \mathrm d^3 \mathbf r
In solid state physics is more common to use the vector potential (the derivation will be omitted) and the perturbing Hamiltonian is:
\mathbf H_{p0}(\mathbf r) \approx -\frac{e}{m_0}\mathbf A \cdot \mathbf p
where \mathbf p = -i\hbar\nabla is the momentum operator and \mathbf A is the vector potential:
\mathbf A = \mathbf e \left(\frac{A_0}{2}e^{i(\mathbf k_{op}\cdot \mathbf r - \omega t)} + \frac{A_0}{2}e^{-i(\mathbf k_{op}\cdot \mathbf r - \omega t)} \right)
where \mathbf e is a unitary vector and \mathbf k_{op} is the wavevector of the optical field inside the material.
The second term can be dropped because it correspond to emission, and therefore the Hamiltonian takes the form:
\mathbf H_{p0}(\mathbf r) = -\frac{e A_0}{2m_0}e^{i \mathbf k_{op}\cdot \mathbf r} \mathbf e \cdot \mathbf p
and the total Hamiltonian is:
\mathbf H_p(\mathbf r,t) = \mathbf H_{p0}(\mathbf r) e^{-i\omega t}
Unitary transition rate
To proceed, it is necessary to know the shape of the wavefunctions, and the assumption is that they are in Bloch state:
\begin{aligned} & \psi_i(\mathbf r) = C_iu_v(\mathbf r)e^{i\mathbf k_v\cdot \mathbf r} \\ & \psi_f(\mathbf r) = C_iu_c(\mathbf r)e^{i\mathbf k_c\cdot \mathbf r} \end{aligned}
The assumption (which works well for a range of practical situation) is that u_v(\mathbf r) and u_c(\mathbf r) are not dependent from \mathbf k. We chose to normalize them over a unit cell, so that:
\int_{\text{cell}} u_v(\mathbf r)u_v(\mathbf r) \mathrm d \mathbf r^3 = 1
Normalizing the wavefunction:
\int_V \bar \psi_i(\mathbf r)\psi_i(\mathbf r)\mathrm d \mathbf r^3 = C_i^2\int_V u_v(\mathbf r)e^{-i\mathbf k_v\cdot \mathbf r} u_v(\mathbf r)e^{i\mathbf k_v\cdot \mathbf r}\mathrm d \mathbf r^3 = C_i^2 N \int_{\text{cell}} u_v(\mathbf r)u_v(\mathbf r) \mathrm d \mathbf r^3 = C_i N^2 = 1
And therefore:
C_i = C_f = \frac{1}{\sqrt N}
Applying Fermi’s golden rule:
\langle \psi_f | \mathbf H_{p0} | \psi_i \rangle = -\frac{e A_0}{2m_0N} \int_V \bar u_c(\mathbf r)e^{-i\mathbf k_c\cdot \mathbf r} e^{i \mathbf k_{op}\cdot \mathbf r} (\mathbf e \cdot \mathbf p) \; u_v(\mathbf r)e^{i\mathbf k_v\cdot \mathbf r} \mathrm d^3 \mathbf r
Considering now to operate in transition states near the center of the Brillouin zone, so that |\mathbf k_v| and |\mathbf k_c| are \ll \frac{\pi}{a} and therefore the momentum operator (which applies to u_v(\mathbf r)e^{i\mathbf k_v\cdot \mathbf r}) we consider operates mostly on u_v(\mathbf r) and neglect the operation on e^{i\mathbf k_v\cdot \mathbf r}:
\mathbf p \left(u_v(\mathbf r)e^{i\mathbf k_v\cdot \mathbf r}\right) = \left(\mathbf p u_v(\mathbf r)\right)e^{i\mathbf k_v\cdot \mathbf r} + u_v(\mathbf r)\left(\mathbf p e^{i\mathbf k_v\cdot \mathbf r}\right) \approx \mathbf p u_v(\mathbf r)e^{i\mathbf k_v\cdot \mathbf r}
The polarization is chosen to be along the x axis and substituting:
\langle \psi_f | \mathbf H_{p0} | \psi_i \rangle = -\frac{e A_0}{2m_0N} \int_V e^{i(\mathbf k_c - \mathbf k_v + \mathbf k_{op}) \cdot \mathbf r} \bar u_c(\mathbf r) p_x \; u_v(\mathbf r) \mathrm d^3 \mathbf r
In typical materials, \mathbf k_{op} is also varying slowly inside the material, so this factor:
e^{i(\mathbf k_c - \mathbf k_v + \mathbf k_{op}) \cdot \mathbf r} \approx e^{i(\mathbf k_c - \mathbf k_v + \mathbf k_{op}) \cdot \mathbf R_m}
can be considered constant over a unit cell, and taking the position of the center \mathrm R_m:
\langle \psi_f | \mathbf H_{p0} | \psi_i \rangle = -\frac{e A_0}{2m_0N} \sum_m e^{i(\mathbf k_c - \mathbf k_v + \mathbf k_{op}) \cdot \mathbf R_m} \int u_c(\mathbf r) p_x \; u_v(\mathbf r) \mathrm d^3 \mathbf r
Defining:
p_{cv} \equiv \langle c | p_x | v \rangle = \int u_c(\mathbf r) p_x \; u_v(\mathbf r) \mathrm d^3 \mathbf r
then:
\langle \psi_f | \mathbf H_{p0} | \psi_i \rangle = -\frac{e A_0}{2m_0N} p_{cv} \sum_m e^{i(\mathbf k_c - \mathbf k_v + \mathbf k_{op}) \cdot \mathbf R_m}
The summation since it is oscillatory, it will average to zero unless:
\mathbf k_c - \mathbf k_v + \mathbf k_{op} = 0
With this condition:
\sum_m e^{i(\mathbf k_c - \mathbf k_v + \mathbf k_{op}) \cdot \mathbf R_m} = \sum_m e^{0} = N
Putting this together gives:
\langle \psi_f | \mathbf H_{p0} | \psi_i \rangle = -\frac{e A_0}{2m_0} p_{cv}
So the relationship between the wavefunctions that must add up to zero; and the Fermi’s golden rule gives a transition rate:
w_{if} = \frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \delta(E_f - E_i - \hbar\omega)
Total transition rate
Once a single transition rate is known, it is possible to compute the total transition rate W_{tot} that is necessary for the optical absorption coefficient \alpha it is necessary to sum all the contributions:
W_{tot} = \frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \sum_i \sum_f \delta(E_c - E_c - \hbar\omega)
with the approximation that p_{cv} is not dependent of \mathbf k. Also since:
\mathbf k_c = \mathbf k_v + \mathbf k_{op}
the final state can be dropped and since |\mathbf k_{op}| is a small fraction of the Brillouin zone will be neglected then:
\mathbf k_c = \mathbf k_v = \mathbf k
That means that the optical transition are vertical in the energy-momentum diagram. Then (introducing the concept of spin):
W_{tot} = \frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \sum_{\mathbf k,\text{spin}} \delta(E_c(\mathbf k) - E_v(\mathbf k) - \hbar\omega)
Considering a unit volume and the density in k-space g({\mathbf k}):
\sum_{\mathbf k,\text{spin}} \approx 2\int_{\mathbf k} g({\mathbf k})\mathrm d^3 {\mathbf k}
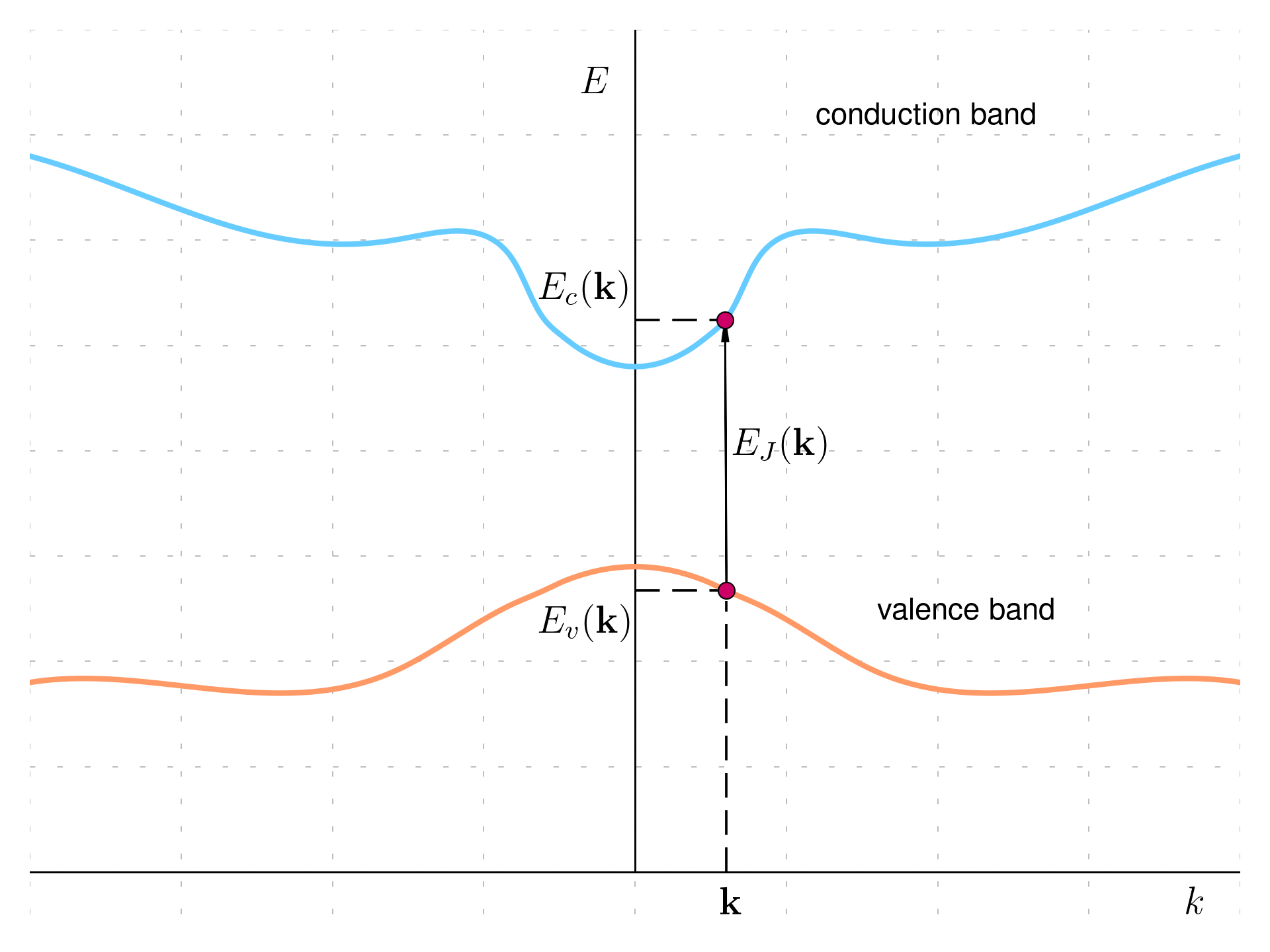
Assuming parabolic bands, the energy separation between the valence and the conduction band for a specific \mathbf k as:
E_J(\mathbf k) = E_c(\mathbf k) - E_v(\mathbf k) = \frac{\hbar^2k^2}{2}\left(\frac{1}{m_{eff_{e}}} + \frac{1}{m_{eff_{v}}}\right) + E_g = \frac{\hbar^2k^2}{2\mu_{eff}} + E_g
with a reduced mass:
\frac{1}{\mu_{eff}} \equiv \frac{1}{m_{eff_{e}}} + \frac{1}{m_{eff_{v}}}
In the same way it was possible to define a density energy of states, it is possible to define a joint density of states (g_J(E_J)) as (accounting for the two spins):
g_J(E_J) \mathrm dE_J = 2g(\mathbf k) d^3 \mathbf k
It is possible to repeat the same argument as the density of state in energy here for a reduce mass \mu_{eff} and derive the density of transition per unit of photon energy:
g_J(E_J) = \frac{1}{2\pi^2}\left(\frac{2\mu_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{E_J - E_g}
Substituting into the total transition rate formula:
\begin{aligned} W_{tot} & = \frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \sum_{\mathbf k,\text{spin}} \delta(E_c(\mathbf k) - E_v(\mathbf k) - \hbar\omega) = \frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \left(\int_{\mathbf k} 2 g({\mathbf k})\mathrm d^3\right) {\mathbf k} \delta(E_c(\mathbf k) - E_v(\mathbf k) - \hbar\omega) \\ & = \frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \int_{E_J \ge E_g}\frac{1}{2\pi^2}\left(\frac{2\mu_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{E_J - E_g} \delta(E_J - \hbar\omega)\mathrm d E_J \end{aligned}
Integrating the delta function gives:
W_{tot} = \frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \frac{1}{2\pi^2}\left(\frac{2\mu_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{\hbar\omega - E_g}
Absorption coefficient
The final step is to compute the absorption coefficient \alpha (the probability of a photon per unit length) as function of the total transition rate W_{tot}; for a photon with energy \hbar\omega the number of photon incident per unit area per second is:
n_p \equiv \frac{I}{\hbar\omega}
where I is the optical intensity so:
\alpha = \frac{W_{tot}}{n_p} = \frac{W_{tot}\hbar\omega}{I}
The intensity (from electromagnetism) can be expressed as:
I = \frac{n_rc\varepsilon_0\omega^2 A_0}{2}
where n_r is the refractive index, c the speed of light and \varepsilon_0 the permittivity of free space. Putting all together:
\begin{aligned} \alpha & = \frac{W_{tot}}{n_p} = \frac{W_{tot}\hbar\omega}{I} = \frac{2\hbar\omega}{n_rc\varepsilon_0\omega^2 A_0}\frac{2\pi}{\hbar}\frac{e^2 A_0^2}{4m_0^2} |p_{cv}|^2 \frac{1}{2\pi^2}\left(\frac{2\mu_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{\hbar\omega - E_g} \\ & = \frac{e^2}{2\pi m_0^2 c\varepsilon_0}\frac{1}{n_r\omega} |p_{cv}|^2\left(\frac{2\mu_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{\hbar\omega - E_g} \end{aligned}
Often |p_{cv}|^2 is express in energy using the parameter:
E_p = \frac{2}{m_0}|p_{cv}|^2
So that the absorption coefficient becomes:
\begin{aligned} \alpha & = \frac{\hbar e^2}{4\pi m_0 c\varepsilon_0}\frac{1}{n_r} \frac{E_p}{\hbar \omega} \left(\frac{2\mu_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{\hbar\omega - E_g} \\ & = \frac{\pi \hbar e^2}{2m_0 c\varepsilon_0}\frac{1}{n_r} \frac{E_p}{\hbar \omega} g_J(\hbar\omega) \end{aligned}
In direct gap semiconductors, this optical absorption model gives us an absorption that rises as the square root of the photon energy’s excess energy above the band gap energy E_g; there are many other effect to consider for doing optical calculation in semiconductors, but this model is used often as the starting point for real calculations.