Crystals
Density of states in quantum wells
Density of states in quantum wires
Introduction
A crystal is a solid material whose constituents, such as atoms, molecules, or ions, are arranged in a highly ordered microscopic structure, forming a lattice that extends in all directions.
The building block of this repetitive pattern is known as the unit cell, the smallest structural unit that reflects the symmetry and structure of the entire crystal. It acts like a three-dimensional pattern from which the crystal is constructed through repetition.

Lattice vectors are mathematical descriptions of the edges of the unit cell. These vectors are used to define the geometry of the unit cell and to describe the positions of points within the lattice, enabling the replication of the unit cell in all spatial directions to form the complete crystal structure. This orderly pattern endows crystals with unique optical, thermal, and electrical properties, making them crucial in various applications ranging from electronic devices to pharmaceuticals.
The set of lattice vectors consists of all the vectors that links point in this lattice:
\mathbf R = n_1 \mathbf a_1 + n_2 \mathbf a_2 + n_3 \mathbf a_3
These link the same point of one cell to another.
In crystallography, Bravais lattices represent the distinct categories of lattice systems that can be created using lattice points in two or three dimensions. These lattices are classified based on the cell’s geometry and the relative positions of the points within the cell.
In two dimensions, there are 5 Bravais lattices:
- Square lattice: Characterized by orthogonal axes of equal length.
- Rectangular lattice: Features orthogonal axes of different lengths.
- Centered rectangular lattice: Similar to the rectangular lattice but with an additional point at the center.
- Hexagonal lattice: Features axes at 120-degree angles, with equal length, forming a regular hexagonal pattern.
- Oblique lattice: Axes are neither orthogonal nor of equal length, forming an oblique angle.
In three dimensions, there are 14 Bravais lattices, grouped into seven crystal systems:
-
Cubic (3 lattices):
- Simple cubic (P): All axes are orthogonal and of equal length.
- Body-centered cubic (I): A simple cubic lattice with an additional lattice point at the center of the cube.
- Face-centered cubic (F): A simple cubic lattice with additional lattice points at the center of each face.
-
Tetragonal (2 lattices):
- Simple tetragonal (P): Axes are orthogonal, with two axes of equal length and the third of a different length.
- Body-centered tetragonal (I): A simple tetragonal lattice with an additional point at the center.
-
Orthorhombic (4 lattices):
- Simple orthorhombic (P): All axes are orthogonal and of different lengths.
- Base-centered orthorhombic (C): Similar to simple orthorhombic but with additional points at the centers of two opposite faces.
- Body-centered orthorhombic (I): A simple orthorhombic lattice with an additional point at the center.
- Face-centered orthorhombic (F): A simple orthorhombic lattice with additional points at the center of each face.
-
Hexagonal (1 lattice):
- Simple hexagonal (P): One axis is of different length from the other two, which are of equal length and meet at 120 degrees.
-
Rhombohedral (1 lattice):
- Simple rhombohedral (R): Axes of equal length that are neither orthogonal nor perpendicular but are inclined at the same angle.
-
Monoclinic (2 lattices):
- Simple monoclinic (P): Axes are of different lengths; two axes are perpendicular, the third is at an angle to these.
- Base-centered monoclinic (C): Similar to simple monoclinic but with additional points at the centers of two opposite faces.
-
Triclinic (1 lattice):
- Simple triclinic (P): The most general form with no axes of equal length and no angles at 90 degrees, having the least symmetry among all the lattices.
Each of these lattices provides a framework that describes how to replicate the unit cells throughout space to form a crystal. These classifications are fundamental to understanding crystal properties and behavior in various scientific and industrial applications.
Zinc-blende lattice
The zinc-blende lattice, also known as sphalerite structure, is a cubic crystal structure that resembles the diamond lattice. It is characterized by two interpenetrating face-centered cubic (fcc) lattices, offset along the body diagonal of the cube by one quarter of the diagonal’s length. This arrangement forms a cubic unit cell with four atoms per unit cell—two of each type, typically represented by a metal (like zinc) and a non-metal (like sulfur).
The name “zinc-blende” comes from the natural mineral sphalerite, which is zinc sulfide (ZnS) and commonly known as zinc blende. This mineral typically appears in the form of crystals resembling the crystallographic structure that bears its name. The lattice is a fundamental structure for many binary semiconductors like GaAs, InP, ZnS, among others, which share the same type of tetrahedral bonding between their constituent atoms.
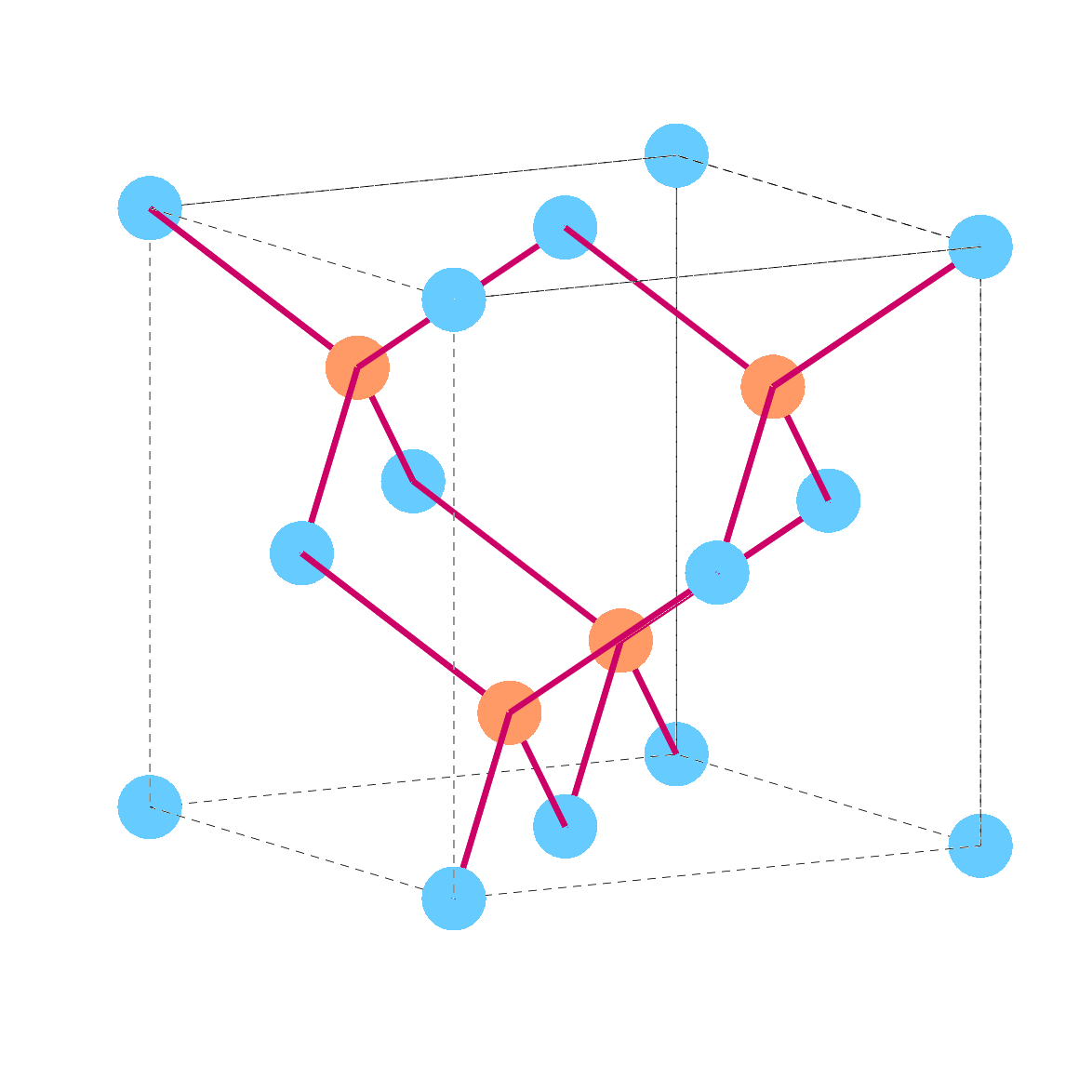
In the picture, the black lines are just for the purpose of showing the square but are not physical, the atomic bond is the red line.
It is easy to see why this is a face-centered cubic lattice, as the blue atoms are located in the vertex and in the center of the face; it is not visible from the picture, but the orange atoms are in the same disposition, but it would be necessary to consider adjacent cubes for fully visualize it.
This kind of lattice is the crystal structure for most of III-V and II-VI materials, with the group III (II) atoms on one face-centered lattice, and V (VI) on the interlocking one.
The diamond lattice looks the same (for some group IV materials) and in this case both lattices have the same kind of atoms.
Density of states in k-space
From the Bloch theorem (here) for crystal, that in three dimension takes the form:
\psi(\mathbf r + \mathbf a) = e^{i \mathbf k \cdot \mathbf a}\psi(\mathbf r)
or equivalently:
\psi(\mathbf r) = u(\mathbf r) e^{i \mathbf k \cdot \mathbf a}
with \mathbf a is any crystal lattice vector and u(\mathbf r + \mathbf a) = u(\mathbf r) and considering the three crystal basis vector direction:
k_i = \frac{2\pi n_i}{N_ia_1}, \quad n = 0,\pm 1,\dots, \pm \tfrac{N_i}{2}
and strictly speaking one of the last value should be (either +\tfrac{N_i}{2} or -\tfrac{N_i}{2}), but that is not relevant for large crystals.
Based on this definition, it is possible to notice that these k_i are each equally spaced:
\delta k_i = \frac{2\pi}{N_i a_i} = \frac{2\pi}{L_i}
as the length of the crystal in one direction is L_i = N_i a_i.
It is then possible to draw a three dimensional diagram with axis k_i to show the allowed values of \mathbf k; in two dimensions will look similar to the crystal lattice above.
This is called reciprocal lattice, and if we consider the volume of a cell of this lattice, it is:
\delta V_k = \prod \delta k_i = \frac{(2\pi)^3}{\prod L_i} = \frac{(2\pi)^3}{V}
It is possible to define a density of states in k-space as:
\frac{1}{\delta V_k} = \frac{V}{(2\pi)^3}
Then, since this is proportional to the volume V, it is possible to define a density of state in k-space per unit volume, which is simply:
g(\mathbf k) = \frac{1}{(2\pi)^3}
and it is independent from the material.
Density of states in energy
Differently that the density in k space, the density of states in energy depends from the band structure, and the relationship between E and \mathbf k need to be known.
In the case of an isotropic parabolic band, by definition the states of an energy E all are on spherical surface in the k-space; the number between E and \mathrm dE is the number on a spherical cells.
The energy at the bottom of the band is:
E = \frac{\hbar^2 k^2}{2m_{eff}} + V
Computing k:
r_1 = k = \sqrt{\frac{2m_{eff}}{\hbar^2}(E - V)}
If \mathrm dk is small then:
\left(\frac{\mathrm dE}{\mathrm dk}\right)\mathrm dE = \frac{1}{2}\sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E - V}}\mathrm dE
The expression for the volume of a thin spherical shell between radii k and k + \mathrm dk comes from the formula for the surface area of a sphere and the infinitesimal thickness \mathrm dk.
The surface area A of a sphere of radius k is given by:
A = 4\pi k^2
The volume \mathrm dV of a thin shell with radius k and thickness \mathrm dk is approximately the surface area of the sphere multiplied by the thickness of the shell:
\mathrm dV = A \times dk = 4\pi k^2 \mathrm dk
This infinitesimal volume formula is then:
\mathrm dV = 4\pi k^2 \mathrm dk
In this case:
\begin{aligned} \mathrm dV & = 4\pi k^2 \mathrm dk = 4\pi k^2 \left(\frac{\mathrm dE}{\mathrm dk}\right)\mathrm dE = 4\pi k^2 \frac{1}{2} \sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E - V}}\mathrm dE \\ & = 4\pi \frac{2m_{eff}}{\hbar^2}(E - V) \frac{1}{2} \sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E - V}}\mathrm dE \\ & = 2\pi \left(\frac{2m_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{E - V}\mathrm dE \end{aligned}
The density of states in k space is:
\frac{V}{(2\pi)^3}
And taking into account that there are two spins, the density of state in energy gives:
g(E)\mathrm dE = \frac{2\mathrm dV}{(2\pi)^3} = \frac{1}{2\pi^2}\left(\frac{2m_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{E - V}\mathrm dE
So that the density of states in energy is:
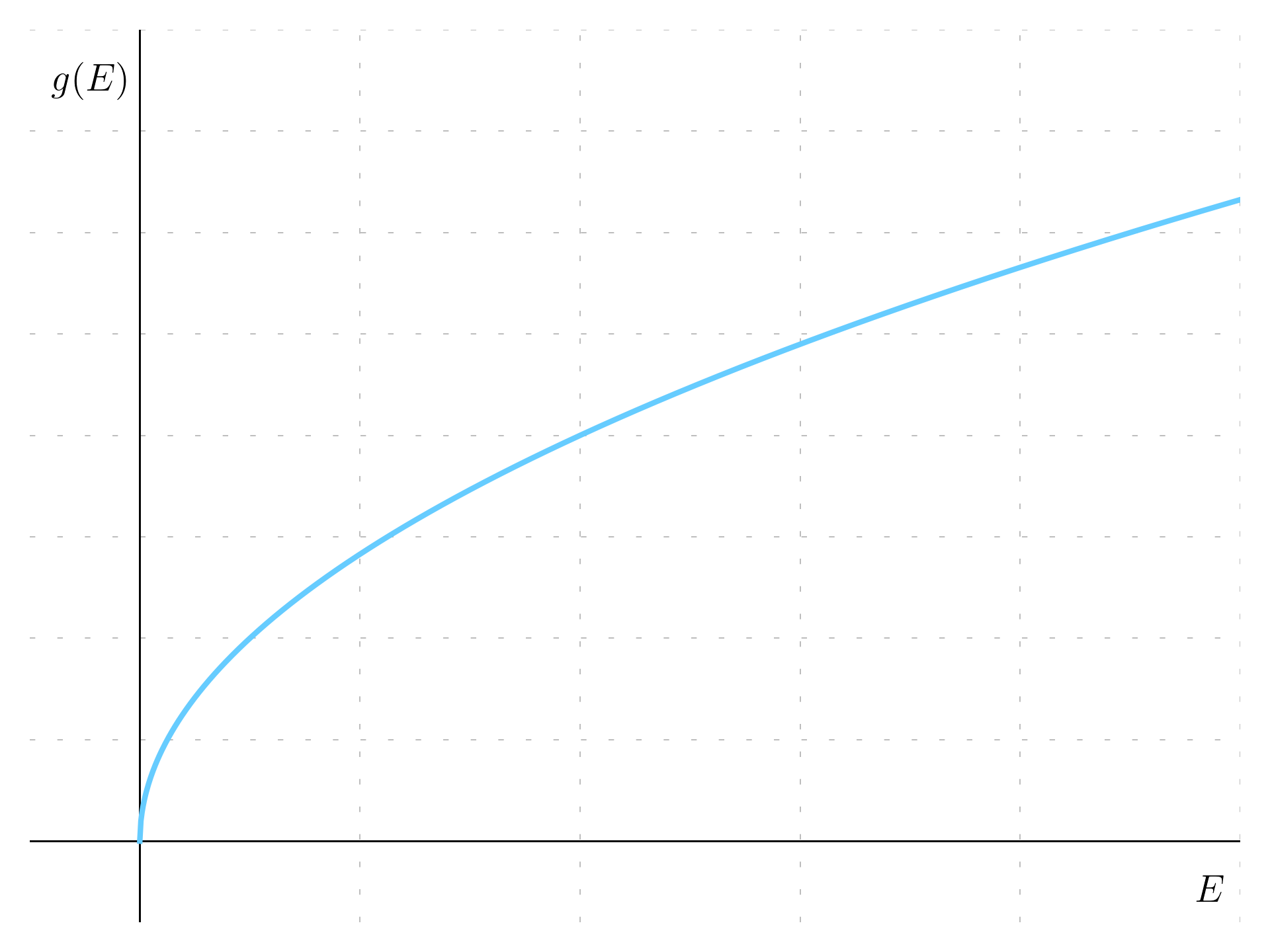
g(E) = \frac{2\mathrm dV}{(2\pi)^3} = \frac{1}{2\pi^2}\left(\frac{2m_{eff}}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{E - V}
and it is a function proportional to \sqrt{E}.
Density of states in quantum wells
A quantum well is a potential well with only discrete energy values. In semiconductor physics, it refers to a thin layer of material sandwiched between layers of materials with a larger bandgap. This configuration confines charge carriers (electrons or holes) to the thin layer, leading to quantized energy levels due to the quantum confinement effect.
Semiconductor heterostructures approximate quantum wells when they involve thin layers of one semiconductor material (with a smaller bandgap) between thicker layers of another material (with a larger bandgap). This arrangement creates a potential well for carriers within the smaller bandgap material.
A common example is a GaAs/AlGaAs heterostructure. Here, a thin layer of Gallium Arsenide (GaAs) is sandwiched between thicker layers of Aluminum Gallium Arsenide (AlGaAs). The GaAs layer acts as the quantum well, trapping electrons or holes, due to its smaller bandgap relative to the surrounding AlGaAs.
Solution to the problem
A way to simulate a quantum well is to to consider an eigenstate of a particle on a one-dimensional potential with a quantum number n and an envelope wavefunction \psi_n(z), and free plain waves in the xy plane with wavevector \mathbf k_{xy}.
The Schrödinger equation:
\left(-\frac{\hbar}{2m_{eff}} \nabla^2 + V(\mathbf r) \right) \psi(\mathbf r) = E\psi(\mathbf r)
can be written as:
\left(-\frac{\hbar}{2m_{eff}} \nabla^2_{xy} - \frac{\hbar}{2m_{eff}} \frac{\partial^2}{\partial x} + V(z) \right) \psi(\mathbf r) = E\psi(\mathbf r)
we will look for a solution with separation of variables as:
\psi(\mathbf r) = \psi_n(z)\psi_{xy}(\mathbf r_{xy})
where \mathbf r_{xy} is the position of the electron in the xy plane.
By substituting the separation of variables solution into the original equation, we obtain:
\left(-\frac{\hbar}{2m_{eff}} \nabla^2_{xy} - \frac{\hbar}{2m_{eff}} \frac{\partial^2}{\partial x} + V(z) \right) (\psi_n(z)\psi_{xy}(\mathbf r_{xy})) = E\psi_n(z)\psi_{xy}(\mathbf r_{xy})
Expanding the Laplacian and derivatives, the equation becomes:
-\frac{\hbar}{2m_{eff}} \left(\psi_n(z) \nabla^2_{xy} \psi_{xy}(\mathbf r_{xy}) + \psi_{xy}(\mathbf r_{xy}) \frac{\partial^2 \psi_n(z)}{\partial z^2}\right) + V(z)\psi_n(z)\psi_{xy}(\mathbf r_{xy}) = E\psi_n(z)\psi_{xy}(\mathbf r_{xy})
Dividing through by \psi_n(z)\psi_{xy}(\mathbf r_{xy}) (assuming neither are zero anywhere within the region of interest), we simplify to:
-\frac{\hbar}{2m_{eff}} \frac{\nabla^2_{xy} \psi_{xy}(\mathbf r_{xy})}{\psi_{xy}(\mathbf r_{xy})} - \frac{\hbar}{2m_{eff}} \frac{\frac{\partial^2 \psi_n(z)}{\partial z^2}}{\psi_n(z)} + V(z) = E
Since the left side must be equal to the constant energy E for all x and \mathbf{r}_{xy}, both terms involving derivatives must individually equate to constants. This implies that we can write:
-\frac{\hbar}{2m_{eff}} \frac{\frac{\partial^2 \psi_n(z)}{\partial z^2}}{\psi_n(z)} + V(z) = E_n
and:
-\frac{\hbar}{2m_{eff}} \frac{\nabla^2_{xy} \psi_{xy}(\mathbf r_{xy})}{\psi_{xy}(\mathbf r_{xy})} = E_{xy}
where E = E_n + E_{xy}.
These equations represent two separate problems: one for motion in the z-direction governed by a potential V(z) and another for free motion in the xy-plane. Each can be solved to find the eigenvalues E_z and E_{xy} and the corresponding eigenfunctions \psi_n(z) and \psi_{xy}(\mathbf r_{xy}).
The second equation, dealing with the xy-plane, is:
-\frac{\hbar}{2m_{eff}} \nabla^2_{xy} \psi_{xy}(\mathbf r_{xy}) = E_{xy} \psi_{xy}(\mathbf r_{xy})
This equation is effectively the time-independent Schrödinger equation for a particle moving freely in the two-dimensional xy-plane. The Laplacian in two dimensions, using Cartesian coordinates (x, y), is given by:
\nabla^2_{xy} = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}
Thus, the equation becomes:
-\frac{\hbar}{2m_{eff}} \left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}\right) \psi_{xy}(x, y) = E_{xy} \psi_{xy}(x, y)
To solve this, we can further assume separability of the wave function in x and y:
\psi_{xy}(x, y) = X(x)Y(y)
Substituting into the equation and dividing both sides by X(x)Y(y) gives:
-\frac{\hbar}{2m_{eff}} \left(\frac{1}{X(x)}\frac{\partial^2 X(x)}{\partial x^2} + \frac{1}{Y(y)}\frac{\partial^2 Y(y)}{\partial y^2}\right) = E_{xy}
Separating variables, we equate each part to a constant such that their sum equals E_{xy}:
-\frac{\hbar}{2m_{eff}} \frac{1}{X(x)}\frac{\partial^2 X(x)}{\partial x^2} = E_x \quad \text{and} \quad -\frac{\hbar}{2m_{eff}} \frac{1}{Y(y)}\frac{\partial^2 Y(y)}{\partial y^2} = E_y
and the energy:
E_{xy} = E_x + E_y
Each of these is a one-dimensional time-independent Schrödinger equation for a free particle. The general solution for a free particle in one dimension is:
\begin{aligned} & X(x) = A e^{ik_x x} + B e^{-ik_x x}\\ & Y(y) = C e^{ik_y y} + D e^{-ik_y y} \end{aligned}
where k_x and k_y are the wave numbers related to E_x and E_y by:
E_x = \frac{\hbar^2 k_x^2}{2m_{eff}}, \quad \quad E_y = \frac{\hbar^2 k_y^2}{2m_{eff}}
Hence, the general solution for \psi_{xy}(x, y) in the xy-plane for a free particle is:
\psi_{xy}(x, y) = (A e^{ik_x x} + B e^{-ik_x x})(C e^{ik_y y} + D e^{-ik_y y})
which can also be expressed in terms of complex exponentials or trigonometric functions depending on boundary conditions or normalization requirements.
Compactly, that can be written as:
\psi_{xy}(\mathbf r_{xy}) = A e^{i\mathbf k_{xy}\cdot \mathbf r}
with:
E_{xy} = \frac{\hbar k^2}{2 m_{eff}}
The first equation:
-\frac{\hbar}{2m_{eff}}\frac{\partial^2 \psi_n(z)}{\partial z^2} \frac{}{} + V(z)\psi_n(z) = E_n\psi_n(z)
it is a particle in a box problem for the envelope with an effective mass m_{eff}.
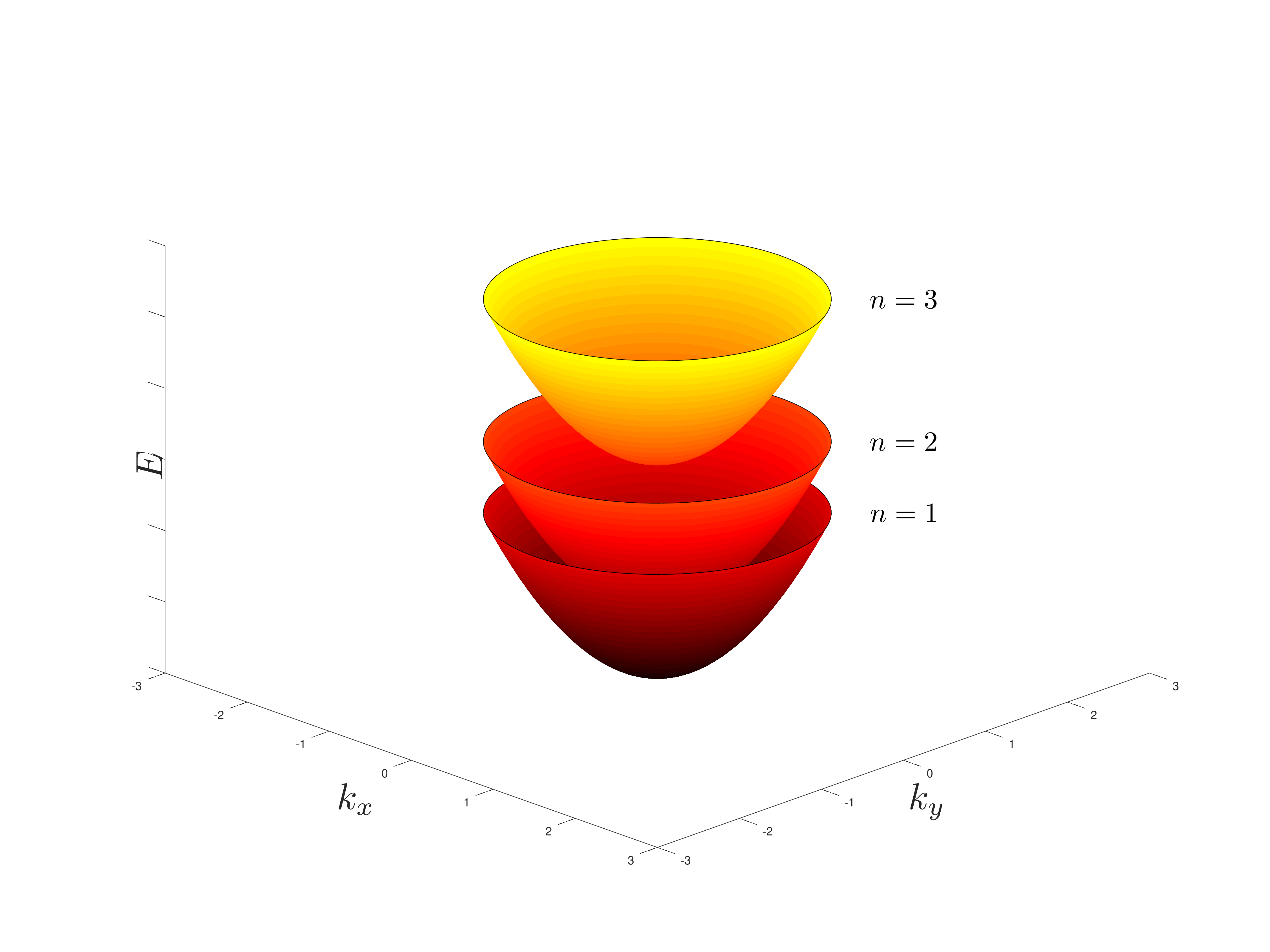
The total allowed energies are the quantum energies associated with a particle in a box E_n, with the additional energies \frac{\hbar k^2}{2 m_{eff}} associated with the motion in the plane, which form what is called subbands which in the particular case are paraboloids, starting from E_n as the lower point.
Density of states calculation
Imposing boundary conditions in the x and y directions will give allowed values of the wavevector in the x direction, k_x spaced by \frac{2\pi}{L_x} where L_x is the length of the crystal in the x direction, and similarly the value of k_y are spaced by \frac{2\pi}{L_y} where L_y is the length of the crystal in the y direction.
Each \mathbf k_{xy} state occupies an area of k spaces equal to (A_{well} = L_xL_y):
\frac{(2\pi)^2}{A_{well}}
The number of states is therefore:
\frac{A_{well}}{(2\pi)^2} \mathrm d^2\mathbf k_{xy}
Therefore, it is possible to define a density of space per unit area as:
g_{2D}\left(\mathbf k_{xy}\right) = \frac{1}{(2\pi)^2}
Considering a well of equal dimensions (L_x = L_y = L), as before, considering a parabolic relationship on the energy:
E_{xy} = \frac{\hbar^2 k^2}{2m_{eff}} + V \left(\frac{\mathrm dE_{xy}}{\mathrm dk}\right)\mathrm dE_{xy} = \frac{1}{2}\sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E_{xy} - V}}\mathrm dE_{xy}
For a small ring on a circular plane, the area \mathrm dA is derived from the circumference of the ring multiplied by its thickness. The circumference of a ring at a radius r is 2\pi r. If the ring has a small thickness \mathrm dr, then the area of the ring is:
dA = 2\pi r \, dr
In this case:
\begin{aligned} dA & = 2\pi k \mathrm dk = 2\pi k \left(\frac{\mathrm dE_{xy}}{\mathrm dk}\right)\mathrm dE_{xy}\\ & = 2\pi \sqrt{\frac{2m_{eff}}{\hbar^2}(E_{xy} - V)}\frac{1}{2}\sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E_{xy} - V}}\mathrm dE_{xy} \\ & = \pi\frac{2m_{eff}}{\hbar^2}\mathrm dE_{xy} \end{aligned}
The density of states in k space is:
\frac{A}{(2\pi)^2}
And taking into account that there are two spins, the density of state in energy gives:
g_{2D}(E)\mathrm dE_{xy} = \frac{2\mathrm dA}{(2\pi)^2} = \frac{m_{eff}}{\pi \hbar^2}\mathrm dE_{xy}
So that the density of states in energy is:
g_{2D}(E) = \frac{2\mathrm dA}{(2\pi)^2} = \frac{m_{eff}}{\pi \hbar^2}
So it is a constant value for E_{xy} > 0 and zero for E_{xy} < 0, and it is a step function jumping at each E_n.
Density of states in quantum wires
A quantum wire is a type of quantum well wherein charge carriers are confined in two dimensions and free to move in the third. Typically, these structures have a rectangular cross-section where one dimension is significantly smaller than the other two, allowing for quantization effects in the smallest dimension. This confinement leads to discrete energy levels similar to those observed in quantum wells, but with freedom of motion along the length of the wire.
Quantum wires are often made from semiconductor materials such as gallium arsenide (GaAs) or indium phosphide (InP) and they are used in electronic and optoelectronic devices, such as high-speed transistors and quantum computing elements, where the quantized energy levels can be exploited to manipulate electronic properties for improved performance.
Solution to the problem
A way to simulate a quantum well is to to consider an eigenstate of a particle on a two-dimensional potential with quantum number n,m and an envelope wavefunction \psi_{nm}(x,y), and free plain waves in the z direction with wavevector \mathbf k.
The Schrödinger equation:
\left(-\frac{\hbar}{2m_{eff}} \nabla^2 + V(\mathbf r) \right) \psi(\mathbf r) = E\psi(\mathbf r)
can be written as:
\left( - \frac{\hbar}{2m_{eff}} \frac{\partial^2}{\partial z} -\frac{\hbar}{2m_{eff}} \nabla^2_{xy} + V(x,y) \right) \psi(\mathbf r) = E\psi(\mathbf r)
we will look for a solution with separation of variables as:
\psi(\mathbf r) = \psi(z)\psi_{nm}(\mathbf r_{xy})
where \mathbf r_{xy} is the position of the electron in the xy plane. we can rewrite the Schrödinger equation by substituting \psi(\mathbf r) = \psi(z)\psi_{nm}(\mathbf{r}_{xy}):
\left( - \frac{\hbar^2}{2m_{eff}} \frac{\partial^2}{\partial z^2} -\frac{\hbar^2}{2m_{eff}} \nabla^2_{xy} + V(x,y) \right) \psi(z)\psi_{nm}(\mathbf{r}_{xy}) = E\psi(z)\psi_{nm}(\mathbf{r}_{xy})
Dividing through by \psi(z)\psi_{nm}(\mathbf{r}_{xy}), we obtain:
-\frac{\hbar^2}{2m_{eff}} \frac{1}{\psi(z)} \frac{\partial^2 \psi(z)}{\partial z^2} - \frac{\hbar^2}{2m_{eff}} \frac{1}{\psi_{nm}(\mathbf{r}_{xy})} \nabla^2_{xy} \psi_{nm}(\mathbf{r}_{xy}) + V(x,y) = E
Let’s denote the separation constants by E_z and E_{xy}, such that:
E = E_z + E_{xy}
Then, splitting the equation into two independent parts, in the z direction:
-\frac{\hbar^2}{2m_{eff}} \frac{\partial^2 \psi(z)}{\partial z^2} = E_z \psi(z)
In the xy-plane:
\left(-\frac{\hbar^2}{2m_{eff}} \nabla^2_{xy} + V(x, y)\right) \psi_{nm}(\mathbf{r}_{xy}) = E_{xy} \psi_{nm}(\mathbf{r}_{xy})
The first equation is a plain wave equation, which will yield solutions of the form:
\psi(z) = A e^{ik_z z} + B e^{-ik_z z}
where k_z = \sqrt{\frac{2m_{eff}E_z}{\hbar^2}}.
The second equation represents a two-dimensional quantum well problem in the xy-plane, which can be treated depending on the specific form of V(x, y). If V(x, y) is a rectangular potential well (details here), solutions \psi_{nm}(\mathbf{r}_{xy}) will be the quantized states for a particle in a box:
\psi_{nm}(x, y) = \sin\left(\frac{n\pi x}{L_x}\right) \sin\left(\frac{m\pi y}{L_y}\right)
with quantized energy levels:
E_{xy,nm} = \frac{\hbar^2\pi^2}{2m_{eff}} \left(\frac{n^2}{L_x^2} + \frac{m^2}{L_y^2}\right)
where L_x and L_y are the dimensions of the well in the x and y directions, respectively, and n, m are integer quantum numbers.
The total allowed energies are the quantum energies associated with a particle in a two-dimensional box E_{nm}, with the additional energies \frac{\hbar k^2}{2 m_{eff}} associated with the motion in the z direction, with subbands which in the particular case are parabolas, starting from E_{nm} as the lower point.
Density of states calculation
Imposing boundary conditions in the z directions will give allowed values of k_z spaced by \frac{2\pi}{L_z} where L_z is the length of the crystal in the z direction; since the number of states is therefore:
\frac{L_z}{2\pi} \mathrm d k_{z}
It is possible to define a density of space per unit length as:
g_{1D}\left(\mathbf k_{z}\right) = \frac{1}{2\pi}
In one dimension, the infinitesimal change is just \mathrm dz, considering a parabolic relationship on the energy:
E_{z} = \frac{\hbar^2 k^2}{2m_{eff}} + V \left(\frac{\mathrm dE_z}{\mathrm dk}\right)\mathrm dE_z = \frac{1}{2}\sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E_z - V}}\mathrm dE_z
therefore:
\mathrm dk_z = \left(\frac{\mathrm dE_z}{\mathrm dk}\right)\mathrm dE_z = \frac{1}{2}\sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E_z - V}}\mathrm dE_z
The density of states in k space is:
\frac{L}{2\pi}
And taking into account that there are two spins and that there are wave traveling forward and backward, the density of state in energy gives:
g_{1D}(E)\mathrm dE_z = \frac{4\mathrm dz}{2\pi} = \frac{1}{\pi}\sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E_z - V}}\mathrm dE_z
So that the density of states in energy is:
g_{1D}(E) = \frac{4\mathrm dz}{2\pi} = \frac{1}{\pi}\sqrt{\frac{2m_{eff}}{\hbar^2}}\frac{1}{\sqrt{E_z - V}}