Particle in a box
Linearization of the Wavefunction
Eigenvalues and Eigensolutions
One dimension
Considering a potential V(x) such as:
V(x) = \begin{cases} 0 & \quad 0 \le x \le L \\ \infty & \quad x < 0, x > L\end{cases}
A particle in this potential is completely free, except at the two ends x = 0 and x = L.
Assumptions:
- No Potential Inside the Box: Inside the box (0 \le x \le L), the potential V(x) = 0. This implies the particle experiences no force and moves freely within these limits.
- Infinite Potential Walls: The potential V(x) is infinite for x < 0 and x > L, creating impenetrable barriers. This confines the particle strictly within the box, as it cannot exist outside these boundaries.
- Wavefunction Boundary Conditions: The wavefunction \psi(x) of the particle is required to be zero at the boundaries (x = 0 and x = L). This condition ensures that the particle does not penetrate or exist beyond the walls.
- Single Particle Model: The analysis focuses on a single, non-relativistic particle. It ignores any interactions with other particles or spin effects, simplifying the system to fundamental quantum behavior within specified limits.
While true infinite potential walls are a physical impossibility, this assumption serves as a useful approximation for describing real phenomena.
In practical applications, very high potential barriers can effectively confine particles, mimicking the infinite wall condition. This model is particularly relevant in the study of quantum dots, nanotechnology, and molecular orbitals, where quantum confinement plays a crucial role in the behavior of electrons and photons. Despite its simplicity, the quantum particle in a box model provides insights into quantum mechanics and the quantization of physical properties.
Linearization of the wavefunction
The first thing to note is that the problem is linear, as the equation that governs it, is the Schrödinger equation, which is, in it time independent form:
\left(-\frac{\hbar}{2m} \nabla^2 + V(\mathbf r) \right) \psi(\mathbf r) = E\psi(\mathbf r)
Therefore, any function c\psi(\mathbf r) is also a solution of the same equation:
\left(-\frac{\hbar}{2m} \nabla^2 + V(\mathbf r) \right) c\,\psi(\mathbf r) = E\,c\,\psi(\mathbf r)
and the constant c factors out. This constant can be used to normalize the wavefunction; since the probability of finding the particle is proportional to the square of the wavefunction \psi(\mathbf r); in general the probability density of finding the particle in a volume \mathrm d \mathbf r is:
\int P(\mathbf r) \mathrm d \mathbf r \propto \int \left| \psi(\mathbf r)\right|^2 \mathrm d \mathbf r
As the overall probability should be 1 (the particle must be somewhere), and using the above linearization property, it is possible to chose a constant |a| and a function \psi_n = a \psi such as:
\int_{-\infty}^\infty P(\mathbf r) \mathrm d \mathbf r = \int_{-\infty}^\infty \left| \psi_n(\mathbf r)\right|^2 = \int_{-\infty}^\infty \left| a \psi(\mathbf r)\right|^2 = 1
So, once a solution \psi(\mathbf r) is found, the integral:
\int_{-\infty}^\infty \left| \psi(\mathbf r)\right|^2 = \frac{1}{|a|} is computed, then the normalized wavefunction \psi_N is obtained as:
\psi_N(\mathbf r) = a\,\psi(\mathbf r) This normalization only sets the magnitude of |a| not the phase, as any phase e^{i\theta} is both not impacting the solution of Schrödinger equation and disappear in the normalization process as the modulus is 1.
Further, when considering the space infinite is requiring that the function which is a solution, its square modulus is Lebesgue integrable (L_2), so periodic functions (like \cos(kx) or \sin(k\mathbf r)) cannot be a solution. A common workaround is to consider only finite volumes (and that is approach taken for example in the particle in a box).
Solution to the problem
Since the wall is infinite high, there is no possibility that the particle is outside the box (\psi(x) = 0, [-\infty,0] \cup [L,\infty]) and that is also 0 at the walls (so that gives the boundary condition). Inside the wall Schrödinger equations became:
-\frac{\mathrm d^2 \psi}{\partial x^2} = k^2\psi, \quad k \equiv \frac{\sqrt{2Em}}{\hbar}
The general solution of this problem is:
\psi(x) = A\,\sin(kx) + B\,\cos(kx) where A and B are arbitrary constants which are fixed by the initial or boundary condition of the problem:
\psi(0) = \psi(L) = 0
and therefore:
\psi(0) = A\sin(0) + B\cos(0) = B = 0
and:
\psi(L) = A\sin(kx) = 0
which gives the trivial solution if A=0 or k=0, or \sin(kx)=0 with:
kL = n\pi,\quad n \in \mathbb N \setminus \{ 0 \}
that is taking into account the relevant index with negative sign as \sin(-\theta) = - \sin(\theta) and A can absorb the sign when matching the initial conditions. Solution are then quantized with values:
k_n = \frac{n\pi}{L},\quad n \in \mathbb N \setminus \{ 0 \}
with the wavefunction that is:
\psi(x) = A_n\sin\left( \frac{n\pi}{L} \right)
The energy is also quantized:
E_n = \frac{\hbar^2k^2}{2m} = \frac{\hbar^2n^2\pi^2}{2mL^2}
It is possible to plot the solutions
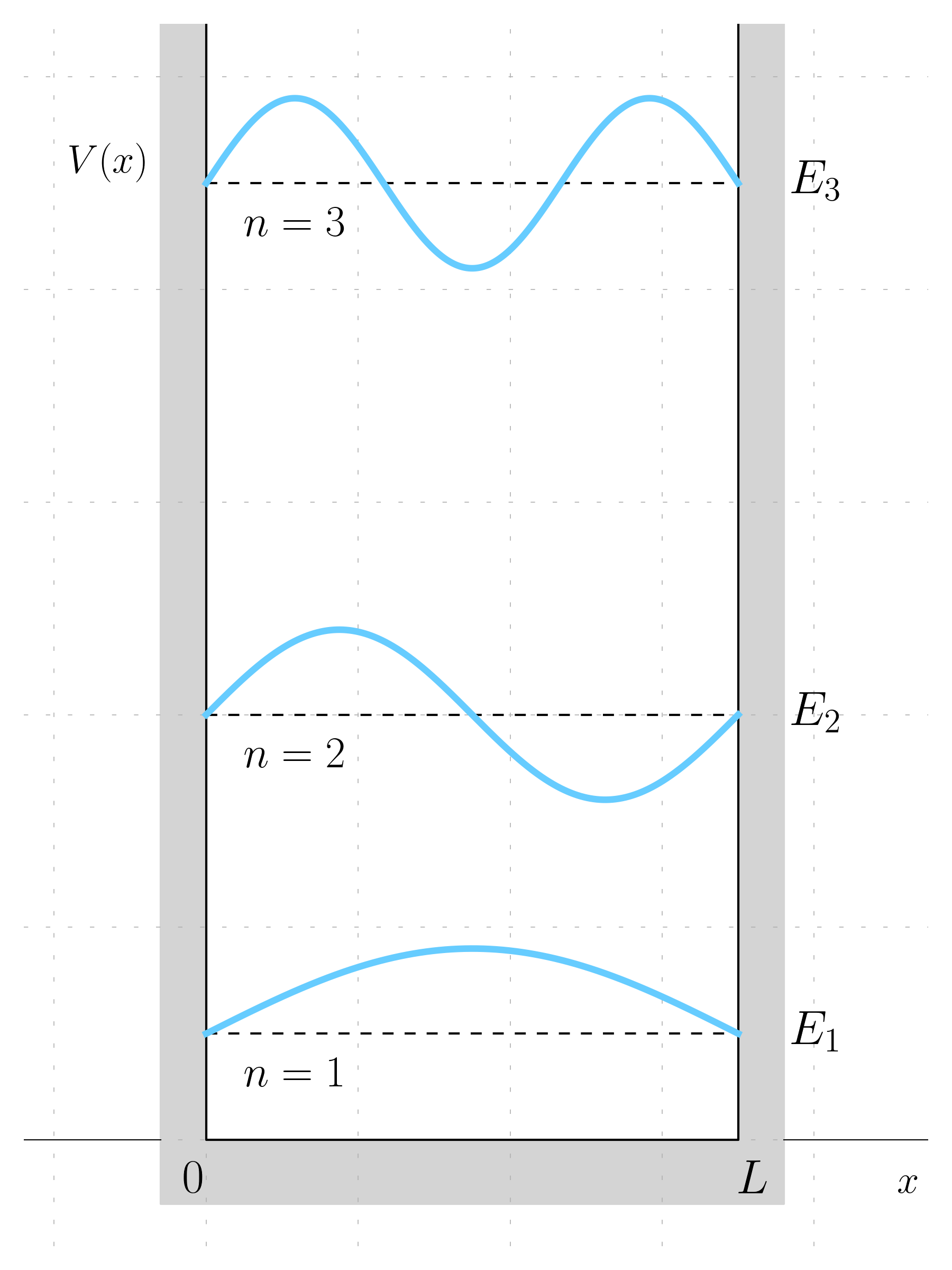
For a choice of n there is a specific level of energy E_n and a specific wavefunction \psi_n(x).
To find A, it is necessary to normalize \psi(x):
\begin{aligned} \int_0^L |\psi(x)|^2 \mathrm dx & = \int_0^L |A|^2 \sin^2(kx)\mathrm dx = |A|^2 \int_0^L \sin^2\left(\frac{n\pi}{L}x\right)\mathrm dx = \frac{|A|^2}{2} \int_0^L\left[ 1- \cos\left(\frac{n\pi}{L}x\right)\right]\mathrm dx \\ & = \frac{|A|^2}{2} \left[ x \bigg|_0^L - \frac{L}{n\pi} \sin\left(\frac{n\pi}{L}x\right) \bigg|_0^L \right] = \frac{|A|^2}{2} \left[ L - \frac{L}{n\pi} \sin\left(n\pi\right) +\frac{L}{n\pi} \sin\left(0\right) \right] = \frac{|A|^2L}{2} = 1 \end{aligned}
The trigonometric identity which was used:
\sin^2(\theta) = \frac{1}{2}[1 - \cos(2\theta)]
Therefore:
|A|^2 = \frac{2}{L}
This formula gives only the magnitude of A, so it possible to chose for example the positive real root:
A = \sqrt{\frac{2}{L}}
which gives the solutions:
\psi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi}{L}x\right)
Eigenvalues and eigensolutions
Considering the particle in a box problem, it was demonstrated that the solutions with a specific energies (the eigenvalues of the problem) have each associated a particular function (the eigenvectors or eigenfunctions of the problem), and the set can be called the eigensolutions of the problem:
\begin{aligned} & E_n = \frac{\hbar^2n^2\pi^2}{2mL^2} \\ & \psi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi}{L}x\right) \\ & n \in \mathbb N \setminus \{ 0 \} \end{aligned}
In the particular case, since E_n is energy, these can be called the eigenergies and \psi_n(x) the energy eigenfunctions.
The function \psi_n(x) have some interesting properties:
- they are alternately even and odd with the center of the well;
- each successive state has one more node, it cross the zero axis one additional time;
- they are mutually orthogonal;
- If the first level of energy is considered 1, the second level of energy is E_2 = 4\, E_1, as it increase \propto n^2.
In similar problems which have a symmetry, the parity aspect (if the solutions are even or odd) is an useful aspect to consider; all the solutions of this problem have a definite parity (they are either even or odd) and it is a common in problems which are symmetric. This fact is mathematically very useful as many integrals are zero (or can be computed doubling half of the solution) precisely for this parity property.
Naturally, the most remarkable finding of this problem is the quantum behavior, as the energy cannot have all values, but only a discrete set of values are allowed:
- there is only a discrete set of possible value of energy;
- there is a minimum level of energy possible for the particle E_1 = \frac{\hbar \pi}{2mL^2}, called zero-point energy. The zero-point energy is due to the fact that the particle is confined within the well; with L smaller this energy is increasing; there is no analogous in classical mechanics;
- the particle is not distributed uniformly over the box, which is something that would not be expected classically; for example there is almost zero probability to find the particle near the walls;
- for n=1 the particle is most likely to be found near the center of the box;
- in higher states there are points within the box in which the particle will never be found;
- the number of zero within the box increase as n-1
Hamiltonian in matrix form
To represent the Hamiltonian it is possible to proceed as follows:
-
The system is defined within a region 0 \leq x \leq L where the potential V(x) = 0 for 0 < x < L and V(x) = \infty for x \leq 0 or x \geq L. This means the particle is confined to a region of space between 0 and L, and cannot be found outside this region.
-
The Hamiltonian operator for a particle in a potential V(x) is given by:
\hat{\mathbf H} = -\frac{\hbar^2}{2m}\frac{\mathrm d^2}{\mathrm dx^2} + V(x)
Since V(x) = 0 within the box, the Hamiltonian simplifies to the kinetic energy term only.
- The eigenfunctions of this Hamiltonian previously calculated, which satisfy the time-independent Schrödinger equation \hat{\mathbf H}| \psi_n \rangle = E_n | \psi_n \rangle, are:
| \psi_n \rangle = \sqrt{\frac{2}{L}}\sin\left(\frac{n\pi x}{L}\right), \quad n=1,2,3,\dots
with corresponding energy eigenvalues:
E_n = \frac{n^2\pi^2\hbar^2}{2mL^2}
- To represent \hat{\mathbf H} as a matrix, we use the eigenfunctions | \psi_n \rangle as a basis. The matrix elements of \hat{ \mathbf H} are given by:
H_{ij} = \langle\psi_i|\hat{\mathbf H}|\psi_j\rangle
Since the Hamiltonian is diagonal in this basis, the matrix elements H_{ij} are zero for i \neq j, and for i = j, H_{ii} = E_i. Therefore, the Hamiltonian matrix is diagonal, with the energy eigenvalues on the diagonal.
Considering a superposition of three states (with opportune coefficients that are coming from normalizing the wavefunction):
| \psi \rangle = a | \psi_1 \rangle + b | \psi_2 \rangle + c | \psi_3 \rangle
with the combination that represents a superposition of the states \psi_1, \psi_2, and \psi_3, with coefficients a, b, and c respectively
The energy expectation value \langle E \rangle is given by:
\langle E \rangle = \langle \Psi | \hat{H} | \Psi \rangle
Substituting \Psi into this expression gives:
\langle E \rangle = \left(a \langle \bar \psi_1 | + b \langle \bar \psi_2 | + c \langle \bar \psi_3 |\right) \hat{H} \left(a | \psi_1 \rangle + b | \psi_2 \rangle + c | \psi_3 \rangle\right)
Given that \hat{H}\psi_n = E_n\psi_n, the Hamiltonian operator acting on each basis state \psi_n gives the energy eigenvalue E_n times the state itself. Computing the inner product and integration, considering the orthogonality of the eigenstates (\langle\psi_i|\psi_j\rangle = \delta_{ij}), the expectation value of the energy becomes:
\langle E \rangle = |a|^2E_1 + |b|^2E_2 + |c|^2E_3
This result shows that the energy expectation value is a weighted sum of the energy eigenvalues, where the weights are the squared magnitudes of the coefficients in the superposition. This accounts for the probability distribution over the energy states due to the superposition of states. Since the energy states are proportional to the ground state with the relation:
E_n = n^2E_1 it is possible to extend the formula for a generic wavefunction combination of k states (which need to be properly normalized):
\langle E \rangle = \sum_{n=1}^k n^2 \left|c_n\right|^2 E_1
Incidentally, the action of the Hamiltonian on the superposition of state is a multiple of the superposition state:
\hat{\mathbf H}|\psi\rangle = \sum_{n=1}^k c_n E_n = \sum_{n=1}^k n^2 c_n E_1
Two dimensions
Considering a potential V(x, y) such as:
V(x) = \begin{cases} 0 & \quad (0 \le x \le L_x) \; \cup \; (0 \le x \le L_y)\\ \infty & \quad x < 0, x > L_x \\ \infty & \quad y < 0, y > L_y \end{cases}
For convenience of representation the pictures show the square interval [-1,1], but the solution can be scaled for any L_x and L_y
The step to get to the solution are similar to the one dimensional case; since the wall is infinite high, there is no possibility that the particle is outside the box and that is also 0 at the walls (so that gives the boundary condition). Inside the wall Schrödinger equations became:
-\frac{\hbar}{2m}\left(\frac{ \partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2}\right) = E\psi
To solve this equation we can try to apply separation of variables; assuming that the wave function \psi(x, y) can be expressed as a product of two functions, one depending only on x and the other only on y:
\psi(x, y) = X(x)Y(y)
Substituting \psi(x, y) = X(x)Y(y) into the Schrödinger equation:
-\frac{\hbar^2}{2m}\left(\frac{\partial^2 (X(x)Y(y))}{\partial x^2} + \frac{\partial^2 (X(x)Y(y))}{\partial y^2}\right) = E X(x)Y(y)
Using the product rule for derivatives, we separate the equation into parts dependent on x and y:
-\frac{\hbar^2}{2m}\left(Y(y) \frac{\partial^2 X(x)}{\partial x^2} + X(x) \frac{\partial^2 Y(y)}{\partial y^2}\right) = E X(x)Y(y)
Dividing through by X(x)Y(y):
-\frac{\hbar^2}{2m}\left(\frac{1}{X(x)}\frac{\partial^2 X(x)}{\partial x^2} + \frac{1}{Y(y)}\frac{\partial^2 Y(y)}{\partial y^2}\right) = E
Since the left-hand side is a sum of terms that depend only on x or only on y, each part must equal a constant. This implies:
\begin{aligned} \frac{\hbar^2}{2m}\frac{1}{X(x)}\frac{\partial^2 X(x)}{\partial x^2} & = E_x \\ -\frac{\hbar^2}{2m}\frac{1}{Y(y)}\frac{\partial^2 Y(y)}{\partial y^2} & = E_y \end{aligned}
With the total energy (the separation constant) being the sum:
E = E_x + E_y
It is now possible to solve these ordinary differential equations separately:
\begin{aligned} \frac{\hbar^2}{2m}\frac{\mathrm d^2 X(x)}{\mathrm d^2 x^2} & = E_x X(x)\\ -\frac{\hbar^2}{2m}\frac{\mathrm d^2 Y(y)}{\mathrm d^2 y^2} & = E_y Y(y) \end{aligned}
The solutions are sinusoidal:
\begin{aligned} & X(x) = B \sin(k_x x) + C \cos(k_x x), \quad k_x \equiv \frac{\sqrt{2E_xm}}{\hbar} \\ & Y(y) = D \sin(k_y y) + E \cos(k_y y), \quad k_y \equiv \frac{\sqrt{2E_ym}}{\hbar} \end{aligned}
It is possible to note that these are the same equations for the one dimensional case, one for each dimensions. The full solution is:
\psi(x, y) = (B \sin(k_x x) + C \cos(k_x x))(D \sin(k_y y) + E \cos(k_y y))
These coefficients and constants B, C, D, E, k_x, k_y are determined based on boundary conditions.
For the current problem, the boundary conditions are:
\begin{aligned} & X(0) = X(L_x) = 0 \\ & Y(0) = Y(L_y) = 0 \end{aligned}
Given these boundary conditions, the solutions for X(x) and Y(y) must be zero at the boundaries, starting from 0:
\begin{aligned} & X(0) = C = 0 \\ & Y(0) = E = 0 \end{aligned}
So the solution don’t have cosinusoidal component:
\begin{aligned} & X(x) = B \sin(k_x x) \\ & Y(y) = D \sin(k_y y) \end{aligned}
Then, at the other boundary L_x and L_y:
\begin{aligned} & X(L_x) = B \sin(k_x L_x) = 0 \\ & Y(L_y) = D \sin(k_y L_y) = 0 \end{aligned}
which leads the constant k_x and k_y to be quantized:
\begin{aligned} & k_{xn_x} = \frac{n_x\pi}{L},\quad n_x \in \mathbb N \setminus \{ 0 \} \\ & k_{yn_y} = \frac{n_y\pi}{L},\quad n_y \in \mathbb N \setminus \{ 0 \} \end{aligned}
The solutions are:
\begin{aligned} & X(x) = B \sin\left(\frac{n_x \pi x}{L_x}\right) \\ & Y(y) = C \sin\left(\frac{n_y \pi y}{L_y}\right) \end{aligned}
The energy is also quantized:
\begin{aligned} & E_{xn_x} = \frac{\hbar^2k_x^2}{2m} = \frac{\hbar^2n_x^2\pi^2}{2mL_x^2} \\ & E_{yn_y} = \frac{\hbar^2k_y^2}{2m} = \frac{\hbar^2n_y^2\pi^2}{2mL_y^2} \end{aligned}
The total energy E of the particle can be determined by summing the energies associated with each motion:
E_{nm} = E_{xn} + E_{ym} = \frac{\hbar^2 k_x^2}{2m} + \frac{\hbar^2 k_y^2}{2m} = \frac{\hbar^2 \pi^2}{2m} \left( \frac{n_x^2}{L_x^2} + \frac{n_y^2}{L_y^2} \right)
The wave function \psi(x, y) for a particle in a two-dimensional infinite box is:
\psi(x, y) = A \sin\left(\frac{n_x \pi x}{L_x}\right) \sin\left(\frac{n_y \pi y}{L_y}\right)
where A = B\,D absorbed both constants.
To normalize the wave function \psi(x, y), we need to ensure that the integral of the absolute square of \psi over the entire area of the box equals one:
\int_0^{L_x} \int_0^{L_y} |\psi(x, y)|^2 \, \mathrm dx \, \mathrm dy = 1
The integral for the normalization condition becomes:
|A|^2 \int_0^{L_x} \sin^2\left(\frac{n_x \pi x}{L_x}\right) \, \mathrm dx \int_0^{L_y} \sin^2\left(\frac{n_y \pi y}{L_y}\right) \, \mathrm dy = 1
Each integral of the squared sine function over its respective interval, given the periodicity and properties of the sine squared function, evaluates to half the interval length:
\begin{aligned} & \int_0^{L_x} \sin^2\left(\frac{n_x \pi x}{L_x}\right) \, dx = \frac{L_x}{2}\\ & \int_0^{L_y} \sin^2\left(\frac{n_y \pi y}{L_y}\right) \, dy = \frac{L_y}{2} \end{aligned}
Thus, the normalization condition simplifies to:
\begin{aligned} & |A|^2 \left(\frac{L_x}{2}\right) \left(\frac{L_y}{2}\right) = 1 \\ & |A|^2 = \frac{4}{L_x L_y} \\ & A = \frac{2}{\sqrt{L_x L_y}} \end{aligned}
Therefore, the normalized wave function \psi(x, y) is:
\psi(x, y) = \frac{2}{\sqrt{L_x L_y}} \sin\left(\frac{n_x \pi x}{L_x}\right) \sin\left(\frac{n_y \pi y}{L_y}\right)
It is possible to plot the wavefunction for some values of n_x and n_y.
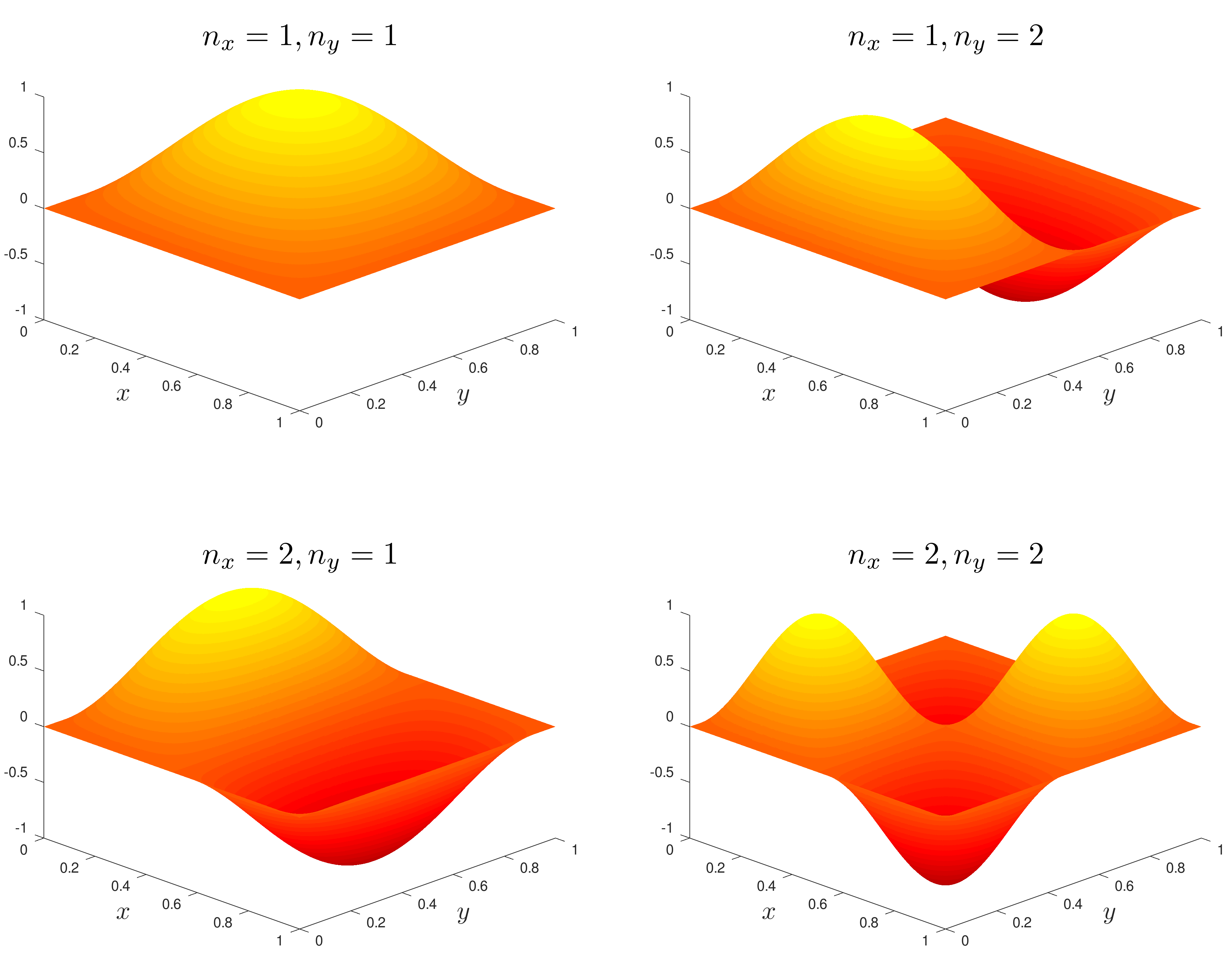
and similarly for the probability densities.
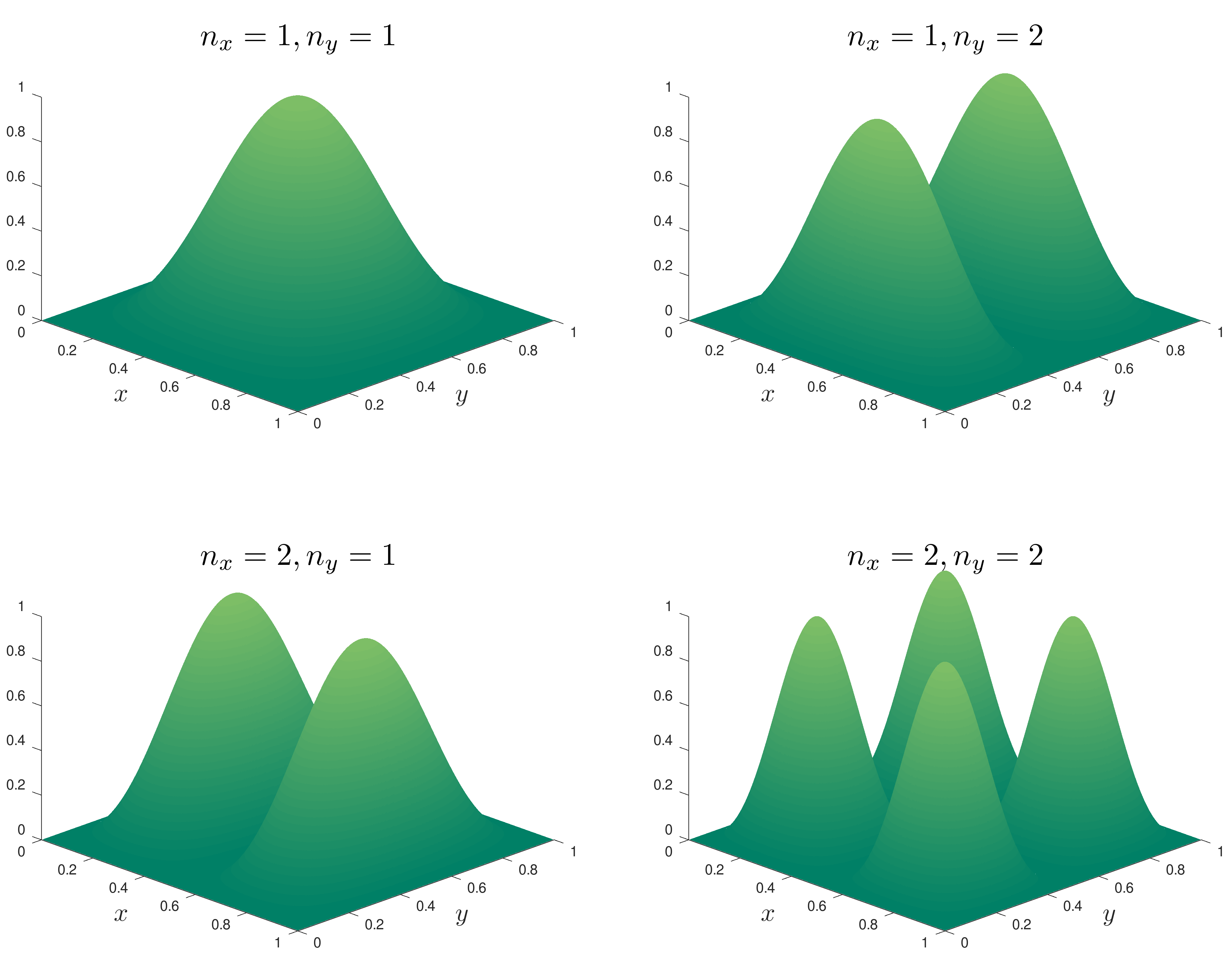
Degeneracy
Degeneracy in quantum mechanics refers to the occurrence of different quantum states having the same energy. This is particularly relevant when discussing systems like particles in boxes where boundary conditions lead to quantized energy levels.
In the context of a particle in a two-dimensional infinite square well (where L_x = L_y = L), the energy levels are given by:
E_{n_x, n_y} = \frac{\hbar^2 \pi^2}{2mL^2} \left(n_x^2 + n_y^2\right)
With the L_x = L_y = L, the symmetry of the system leads to certain energy levels being more frequently degenerate. Here, any pair of quantum numbers (n_x, n_y) that satisfies n_x^2 + n_y^2 = n^2 for the same integer n will have the same energy.
For example: - The energy E_{1,2} and E_{2,1} will be equal. That is noticeable from the graphs, as these two state have the same wavefunction and probability density simply rotated 90^\circ on the xy plane.
The highest degeneracy occurs when there are many different pairs (n_x, n_y) that yield the same sum n_x^2 + n_y^2. This tends to happen more frequently with higher quantum numbers where there are more combinations possible that add up to the same value.
In the specific case of a square box (L_x = L_y), energy levels that are degenerate often include permutations and combinations of (n_x, n_y) such as (1, 2) and (2, 1), indicating that swapping the quantum numbers does not change the energy due to the symmetry of the system.
To find how many states share the same energy level in a square box, one needs to count all unique pairs (n_x, n_y) that satisfy the equation n_x^2 + n_y^2 = k for a constant k.
This characteristic of quantum systems leads to interesting properties and is crucial for understanding the electronic structure of materials, where degeneracy plays a significant role in determining material properties like electrical conductivity and magnetism.