Absorption and Emission
Hamiltonian for Electron-Photon Interaction
Multiple Photons Spontaneous Emission
Multiple Photons Stimulated Emission
Total Spontaneous Emission Rate
Introduction
Perturbation theory (detail here for the quantum mechanics description of the method) with annihilation and creation operators is a powerful technique in quantum mechanics used to analyze systems subjected to small disturbances. This method employs the formalism of annihilation (\mathbf a) and creation (\mathbf a^\dagger) operators (here), in particular when describing different kind of particles.
By treating the perturbation as an interaction term within the Hamiltonian, one can use these operators to systematically compute corrections to the energy levels and states of the system. This approach is particularly useful for understanding processes such as absorption and emission of photons, where transitions between quantum states are mediated by these operators.
Hamiltonian for electron-photon interaction
The Hamiltonian for an electric dipole is:
\mathbf H = e \mathbf E \cdot \mathbf r
With the theory derived, using the electric field operator for a set of electrons (derivation here and then it summed over all the particles) it becomes:
\mathbf H = \sum_{n=1}^N e i\sum_\lambda \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf u_\lambda(\mathbf r_n) \cdot \mathbf r_n
To transform it in the occupation number representation it is necessary to use the wavefunction operator and the results of the second quantization (here):
\begin{aligned} \mathbf {\hat H} & = \int \hat \psi^\dag \mathbf H \hat \psi \mathrm d^3 \mathbf r_1 \dots \mathrm d^3 \mathbf r_N \\ & = \int \hat \psi^\dag \sum_{n=1}^N e i\sum_\lambda \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf u_\lambda(\mathbf r_n) \cdot \mathbf r_n \hat \psi \mathrm d^3 \mathbf r_1 \dots \mathrm d^3 \mathbf r_N \\ & = \sum_\lambda \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \int \hat \psi^\dag \sum_{n=1}^N e i\sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf u_\lambda(\mathbf r_n) \cdot \mathbf r_n \hat \psi \mathrm d^3 \mathbf r_1 \dots \mathrm d^3 \mathbf r_N \end{aligned}
Defining:
\mathbf {\hat H_{\lambda, \mathbf r}} = \sum_{n=1}^N e i\sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf u_\lambda(\mathbf r_n) \cdot \mathbf r_n = \sum_{n=1}^N \mathbf {\hat H}_{\lambda, \mathbf r_n}
\mathbf {\hat H_{\lambda, \mathbf r_n}} is a single particle fermion Hamiltonian, and therefore:
\mathbf {\hat H} = \sum_\lambda \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \int \hat \psi^\dag \mathbf {\hat H_{\lambda, \mathbf r}} \hat \psi \mathrm d^3 \mathbf r_1 \dots \mathrm d^3 \mathbf r_N = \sum_{\lambda,j,k} \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k
where:
\mathbf {\hat H}_{\lambda,jk} \equiv \int \phi_j(\mathbf r_n) {\hat H}_{\lambda, \mathbf r_n}\phi_k(\mathbf r_n) \mathrm d^3 \mathbf r_n
The sum over N of the contribution of all single particle cancel out from the \frac{1}{N} normalization factor as demonstrated in the second quantization derivation section.
In the Hamiltonian expression (using the commutation between fermion and boson operators to re-write it):
\mathbf {\hat H} = \sum_{\lambda,j,k} \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k\left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right)
The specific form of the creation and annihilation operators identifies specific processes, such as emission or absorption, based on the starting state of the system. For example:
Absorption:
- In absorption, a photon is absorbed by the system, raising the system from a lower energy state to a higher energy state.
- If the system starts in a state |n\rangle and absorb a photon, the annihilation operator \mathbf{a}_\lambda is involved. The system transitions to a state |n-1\rangle:
\mathbf{a}_\lambda |n\rangle \rightarrow |n-1\rangle
Emission:
- In stimulated emission, an incoming photon induces the emission of another photon, causing the system to transition from a higher energy state to a lower energy state.
- In spontaneous emission, the system naturally transitions from a higher energy state to a lower energy state, emitting a photon without the need for an external photon
- If the system starts in a state |n\rangle and emits a photon, the creation operator \mathbf{a}_\lambda^\dag is involved. The system transitions to a state |n+1\rangle:
\mathbf{a}_\lambda^\dag |n\rangle \rightarrow |n+1\rangle
In the Hamiltonian expression, these processes can be identified by the respective operators:
- For absorption, the term involving \mathbf{a}_\lambda indicates the annihilation of a photon.
- For stimulated emission, the term involving \mathbf{a}_\lambda^\dag indicates the emission of a photon.
- For spontaneous emission, the transition occurs naturally due to the interaction Hamiltonian, with the emission of a photon described by \mathbf{a}_\lambda^\dag.
Thus, the Hamiltonian can be written to encompass these processes:
\mathbf{\hat{H}} = \sum_{\lambda,j,k} \left( \mathbf{a}_\lambda \mathbf{\hat{H}}_{\lambda,jk} \mathbf{b}^\dag_j \mathbf{b}_k + \mathbf{a}_\lambda^\dag \mathbf{\hat{H}}_{\lambda,jk} \mathbf{b}^\dag_j \mathbf{b}_k \right)
In this form, the Hamiltonian explicitly represents the processes of absorption (via \mathbf{a}_\lambda) and emission (via \mathbf{a}_\lambda^\dag), providing a comprehensive framework for analyzing electron-photon interactions.
It is possible to apply to this Hamiltonian a first order time-dependent perturbation theory (here) to a few cases.
The rate of change of the coefficients for the first order are:
\dot a_n^{(1)} = \frac{1}{i\hbar} \sum_j a_j^{(0)}e^{i\omega_{nj}t} \langle N_{fn}; N_{bn} | \mathbf H_p |N_{fj};N_{bj}\rangle
where \omega_{nj} = \frac{E_n - E_j}{\hbar} and the perturbing Hamiltonian is the one written above in which the particles are interacting.
It is possible to consider some example of system that start in a specific state q (so that a_q^{(0)} =1,a_{j \ne q}=0) and transitioning to state r; for these the coefficient are:
\dot a_r^{(1)} = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle
Absorption
Let’s assume that there is an electron in state | 1 \rangle and a photon in mode | 1 \rangle.
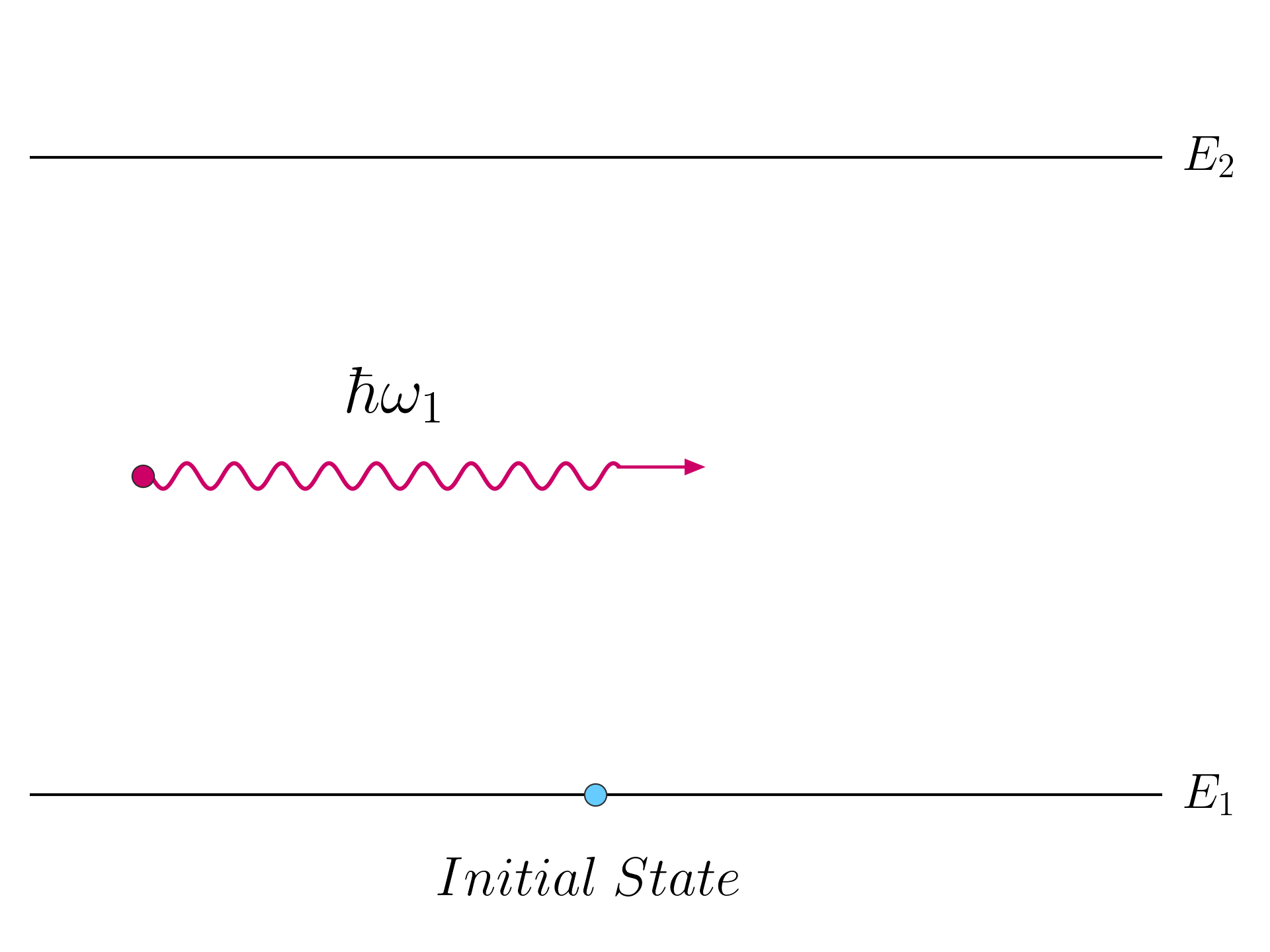
This state can be written as:
| \hat \psi \rangle = \mathbf b_1^\dag \mathbf a_1^\dag | \mathbf 0 \rangle
The total energy for this state is:
E_q = E_b + E_f = E_1 + \hbar\omega_1
The perturbing Hamiltonian multiply by the initial state is:
\begin{aligned} \mathbf H_p | \hat \psi \rangle & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k\left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \mathbf b_1^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_1^\dag \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \mathbf a_1^\dag | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_1^\dag \left(\mathbf a_\lambda \mathbf a_1^\dag - \mathbf a_\lambda^\dag\mathbf a_1^\dag\right) | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \left(\delta_{k1} - \mathbf b_1^\dag\mathbf b_k \right) \left(\delta_{\lambda1} + \mathbf a_1^\dag \mathbf a_\lambda - \mathbf a_\lambda^\dag\mathbf a_1^\dag\right) | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k1} \mathbf b^\dag_j\left(\delta_{\lambda1} - \mathbf a_\lambda^\dag\mathbf a_1^\dag\right) | \mathbf 0 \rangle\\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \left(\delta_{k1} \delta_{\lambda1} \mathbf b^\dag_j| \mathbf 0 \rangle - \delta_{k1} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle\right) \end{aligned}
We have used standard manipulation to push the annihilation operators to the right and the commutation relation for fermions and bosons (recalling that they have a different sign).
There are only two possible choices that give non-zero results (and therefore only two state that might have a non-zero perturbation theory coefficients) as any other state would be orthogonal to these two states and the coefficient will be zero.
The first possibility is to have as final state:
\mathbf b^\dag_j| \mathbf 0 \rangle
which is the state with one electron in state | j \rangle and no photons, so the photon has been absorbed; the energy for this state is just the energy of the electron:
E_r = E_f = E_j
The coefficient for this case is:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf b^\dag_j| \mathbf H_p | \mathbf b_1^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \\ & =\frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 |\mathbf b^\dag_j|\left( \mathbf H_p | \mathbf b_1^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 |\mathbf b^\dag_j| \sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \left(\delta_{k1} \delta_{\lambda1} \mathbf b^\dag_j| \mathbf 0 \rangle - \delta_{k1} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle\right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t}\langle \mathbf 0 |\mathbf b^\dag_j| \sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k1} \delta_{\lambda1} \mathbf b^\dag_j| \mathbf 0 \rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k1} \delta_{\lambda1} \langle \mathbf 0 |\mathbf b^\dag_j| \mathbf b^\dag_j| \mathbf 0 \rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \mathbf {\hat H}_{1,j1} \end{aligned}
With the values of the problem it becomes:
\dot a_r^{(1)} = \frac{1}{i\hbar} e^{i\omega_{rq}t} \mathbf {\hat H}_{1,j1} = \frac{1}{i\hbar} e^{i\frac{E_r - E_q}{\hbar}t} \mathbf {\hat H}_{1,j1} = \frac{1}{i\hbar} e^{i\frac{E_j - E_1 - \hbar\omega_1}{\hbar}t} \mathbf {\hat H}_{1,j1}
We can apply Fermi Golden rules and compute the transition rate:
w_r = \frac{2\pi}{\hbar}\left| \mathbf {\hat H}_{1,j1} \right|^2 \delta\left(E_j - E_1 - \hbar\omega_1\right)
As there are only two energy states (| 1 \rangle and | 2 \rangle), we can substitute. For | j \rangle =| 1 \rangle:
w_r = \frac{2\pi}{\hbar}\left| \mathbf {\hat H}_{1,11} \right|^2 \delta\left(E_1 - E_1 - \hbar\omega_1\right) = \frac{2\pi}{\hbar}\left| \mathbf {\hat H}_{1,11} \right|^2 \delta\left(- \hbar\omega_1\right)
There is no energy that can make the delta unitary.
For | j \rangle =| 2 \rangle:
w_r = \frac{2\pi}{\hbar}\left| \mathbf {\hat H}_{1,21} \right|^2 \delta\left(E_2 - E_1 - \hbar\omega_1\right)
There is a finite transition rate if \hbar \omega_1 is exactly equal to the difference in energies:
\hbar\omega_1 = E_2 - E_1
This process describe an absorption process, starting with one electron in state | 1 \rangle and a photon in mode | 1 \rangle, and ending with an electron in state | 2 \rangle and a photon which is annihilated.
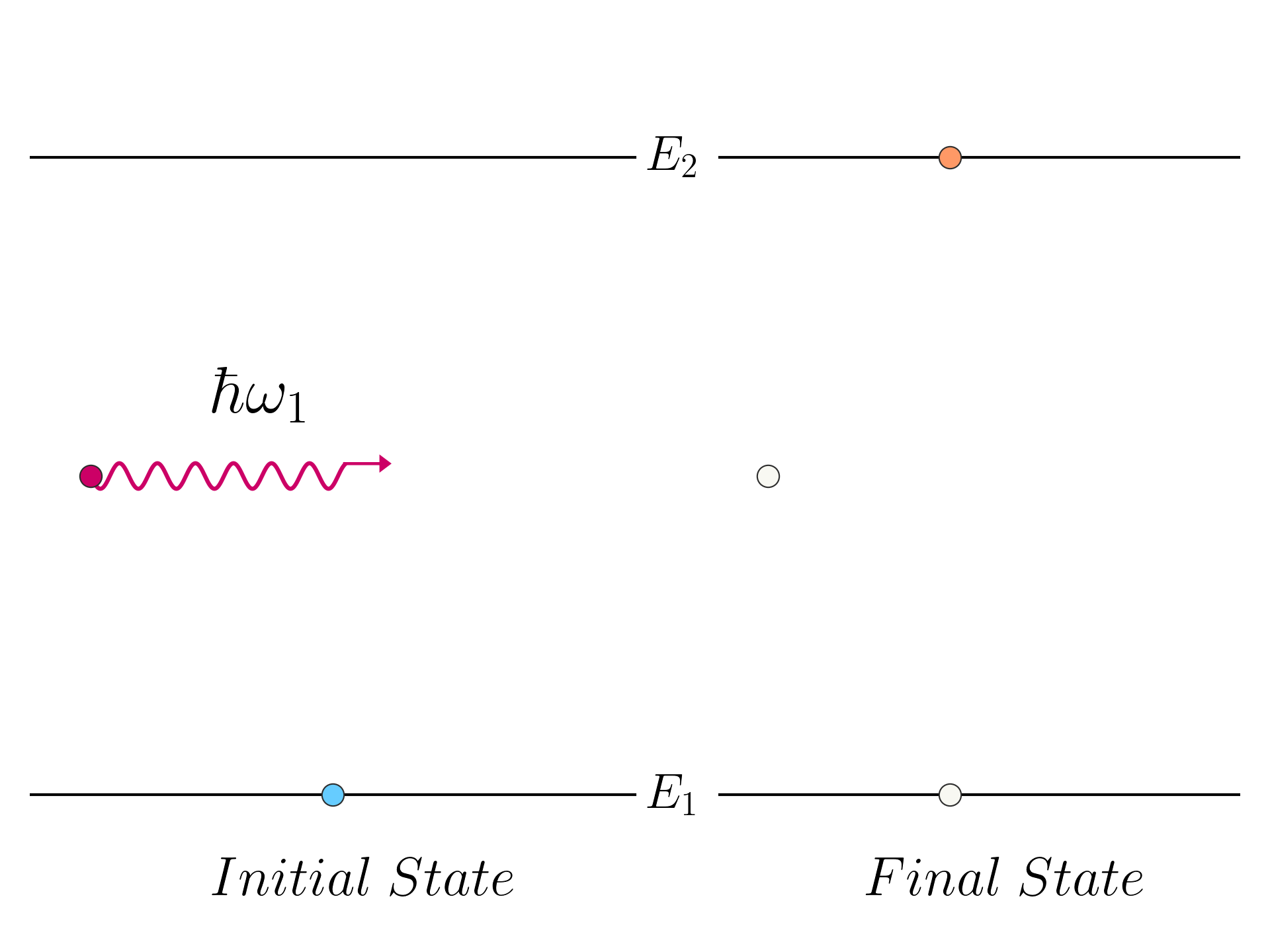
The transition rate can be written as:
w_r = \frac{2\pi}{\hbar}\left| \mathbf {\hat H}_{1,12} \right|^2 \delta\left(E_2 - E_1 - \hbar\omega_1\right)
Using the relationship:
\mathbf {\hat H}_{1,21} = \mathbf {\hat {\bar H}}_{1,12}
And then the modulus is canceling the complex conjugation. This will be useful because a similar term will appear for emission and therefore the above shows that only a set of coefficient is needed.
The second possibility is to have as final state:
\mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle
which is the state with one electron in state | j \rangle and two photons, so and additional photon in the mode | \lambda \rangle has been created. The energy of this state is the sum of the energy of the electron and the energy of the two photons:
E_r = E_b + E_f = E_j + \hbar \omega_\lambda + \hbar \omega_1
The coefficient for this case is:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j | \mathbf H_p | \mathbf b_1^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \\ & =\frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j |\left( \mathbf H_p | \mathbf b_1^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j | \sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \left(\delta_{k1} \delta_{\lambda1} \mathbf b^\dag_j| \mathbf 0 \rangle - \delta_{k1} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle\right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t}\langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j |\sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k1} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t}\sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k1} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \sum_{\lambda} \mathbf {\hat H}_{\lambda,j1} \end{aligned}
With the values of the problem it becomes, for a specific |\lambda \rangle:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t}\mathbf {\hat H}_{\lambda,j1} = \frac{1}{i\hbar} e^{i\frac{E_r - E_q}{\hbar}t} \mathbf {\hat H}_{\lambda,j1} \\ & = \frac{1}{i\hbar} e^{i\frac{E_j + \hbar \omega_\lambda + \hbar \omega_1 - E_1 - \hbar\omega_1}{\hbar}t} \mathbf {\hat H}_{\lambda,j1} = \frac{1}{i\hbar} e^{i\frac{E_j + \hbar \omega_\lambda - E_1}{\hbar}t} \mathbf {\hat H}_{\lambda,j1} \end{aligned}
We can apply Fermi Golden rules and compute the transition rate:
w_r = \frac{2\pi}{\hbar} \left| \mathbf {\hat H}_{\lambda,j1} \right|^2 \delta\left(E_j - E_1 + \hbar\omega_\lambda\right)
Since E_j - E_1 \ge 0 and \hbar \omega_\lambda > 0\, \forall \lambda there is not any combination that makes the delta function unitary, and therefore there are no physical solutions.
Overall, in conclusion, the only possible solution is the absorption of a photon and the transition of the electron from the lower to the higher energy state.
Multiple photons absorption
Let’s assume that there is an electron in state | 1 \rangle and n photons in mode | 1 \rangle. This state can be written as:
| \hat \psi \rangle =\frac{1}{\sqrt{n!}} \mathbf b_1^\dag \left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle
The total energy for this state is:
E_q = E_b + E_f = E_1 + n\hbar\omega_1
The perturbing Hamiltonian multiply by the initial state is:
\begin{aligned} \mathbf H_p | \hat \psi \rangle & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k\left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \frac{1}{\sqrt{n!}} \mathbf b_1^\dag\left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_1^\dag \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right)\left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_1^\dag \left[\mathbf a_\lambda \left(\mathbf a_1^\dag \right)^n - \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n\right] | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \left(\delta_{k1} - \mathbf b_1^\dag\mathbf b_k \right) \left(n \delta_{\lambda 1} \left(\mathbf{a}_1^\dag\right)^{n-1} + \left(\mathbf{a}_1^\dag\right)^n \mathbf{a}_\lambda - \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n\right) | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k1} \mathbf b^\dag_j \left(n \delta_{\lambda 1} \left(\mathbf{a}_1^\dag\right)^{n-1} - \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n\right) | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \left(n \delta_{k1} \delta_{\lambda 1} \mathbf b^\dag_j \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle - \delta_{k1} \mathbf b^\dag_j \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n| \mathbf 0 \rangle \right) \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j1} \mathbf {\hat H}_{\lambda,j1} \left(n \delta_{\lambda 1} \mathbf b^\dag_j \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle - \mathbf b^\dag_j \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n| \mathbf 0 \rangle \right) \\ & = \frac{1}{\sqrt{n!}} \mathbf {\hat H}_{1,j1} \left(n \mathbf b^\dag_j \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle - \mathbf b^\dag_j \left(\mathbf a_1^\dag \right)^{n+1}| \mathbf 0 \rangle \right) \\ \end{aligned}
where we used the commutation definition:
\begin{aligned} \mathbf{a}_\lambda \left(\mathbf{a}_1^\dag\right)^n & = \left[\mathbf{a}_\lambda, \left(\mathbf{a}_1^\dag\right)^n\right] + \left(\mathbf{a}_1^\dag\right)^n \mathbf{a}_\lambda \\ & = n \left(\mathbf{a}_1^\dag\right)^{n-1} [\mathbf{a}_\lambda, \mathbf{a}_1^\dag] + \left(\mathbf{a}_1^\dag\right)^n \mathbf{a}_\lambda \\ & = n \left(\mathbf{a}_1^\dag\right)^{n-1} \delta_{\lambda 1} + \left(\mathbf{a}_1^\dag\right)^n \mathbf{a}_\lambda \\ & = n \delta_{\lambda 1} \left(\mathbf{a}_1^\dag\right)^{n-1} + \left(\mathbf{a}_1^\dag\right)^n \mathbf{a}_\lambda \end{aligned}
The reasoning is the same as previously done and the only allow final state is:
\frac{1}{\sqrt{(n-1)!}}\mathbf b^\dag_2 \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle
which is the state with one electron in state |2\rangle and n-1 photons in state | 1 \rangle, so one photon has been absorbed; the energy for this state is:
E_r = E_b + E_f = E_2 + (n-1)\hbar \omega_1
The coefficient for this case is:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \frac{1}{\sqrt{(n-1)!}}\left(\mathbf{a}_1\right)^{n-1} \mathbf b_2 | \mathbf H_p | \frac{1}{\sqrt{n!}} \mathbf b_1^\dag \left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \\ & =\frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \frac{1}{\sqrt{(n-1)!}}\left(\mathbf{a}_1\right)^{n-1} \mathbf b_2 | \left( \mathbf H_p | \frac{1}{\sqrt{n!}} \mathbf b_1^\dag \left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \frac{1}{\sqrt{(n-1)!}}\left(\mathbf{a}_1\right)^{n-1} \mathbf b_2 | \frac{1}{\sqrt{n!}} \mathbf {\hat H}_{1,21} \left(n \mathbf b^\dag_2 \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle - \mathbf b^\dag_2 \mathbf a_1^\dag\left(\mathbf a_1^\dag \right)^n| \mathbf 0 \rangle \right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \frac{1}{\sqrt{(n-1)!}}\left(\mathbf{a}_1\right)^{n-1} \mathbf b_2 | \frac{1}{\sqrt{n!}} \mathbf {\hat H}_{1,21} n \mathbf b^\dag_2 \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{n}{\sqrt{n}} \mathbf {\hat H}_{1,21} \langle \mathbf 0 | \frac{1}{\sqrt{(n-1)!}}\left(\mathbf{a}_1\right)^{n-1} \mathbf b_2 \frac{1}{\sqrt{(n-1)!}}\mathbf b^\dag_2 \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{n}{\sqrt{n}} \mathbf {\hat H}_{1,21} \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \sqrt{n} \mathbf {\hat H}_{1,21} \end{aligned}
With the values of the problem it becomes:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \sqrt{n} \mathbf {\hat H}_{1,21} = \frac{1}{i\hbar} e^{i\frac{E_r - E_q}{\hbar}t} \sqrt{n} \mathbf {\hat H}_{1,21} \\ & = \frac{1}{i\hbar} e^{i\frac{E_2 + (n-1)\hbar\omega_1 - E_1 - n\hbar\omega_1}{\hbar}t} \sqrt{n} \mathbf {\hat H}_{1,21} = \frac{1}{i\hbar} e^{i\frac{E_2 - E_1 - \hbar\omega_1}{\hbar}t} \sqrt{n} \mathbf {\hat H}_{1,21} \end{aligned}
We can apply Fermi Golden rules and compute the transition rate:
w_r = \frac{2\pi}{\hbar}n \left| \mathbf {\hat H}_{1,21} \right|^2 \delta\left(E_2 - E_1 - \hbar\omega_1\right)
There is a finite transition rate if \hbar \omega_1 is exactly equal to the difference in energies:
\hbar\omega_1 = E_2 - E_1
Using again that:
\mathbf {\hat H}_{1,21} = \mathbf {\hat {\bar H}}_{1,12}
the transition rate is:
w_r = \frac{2\pi}{\hbar}n \left| \mathbf {\hat H}_{1,12} \right|^2 \delta\left(E_2 - E_1 - \hbar\omega_1\right)
Spontaneous emission
Let’s consider an electron in an excited state (state | 2 \rangle) and no photons.
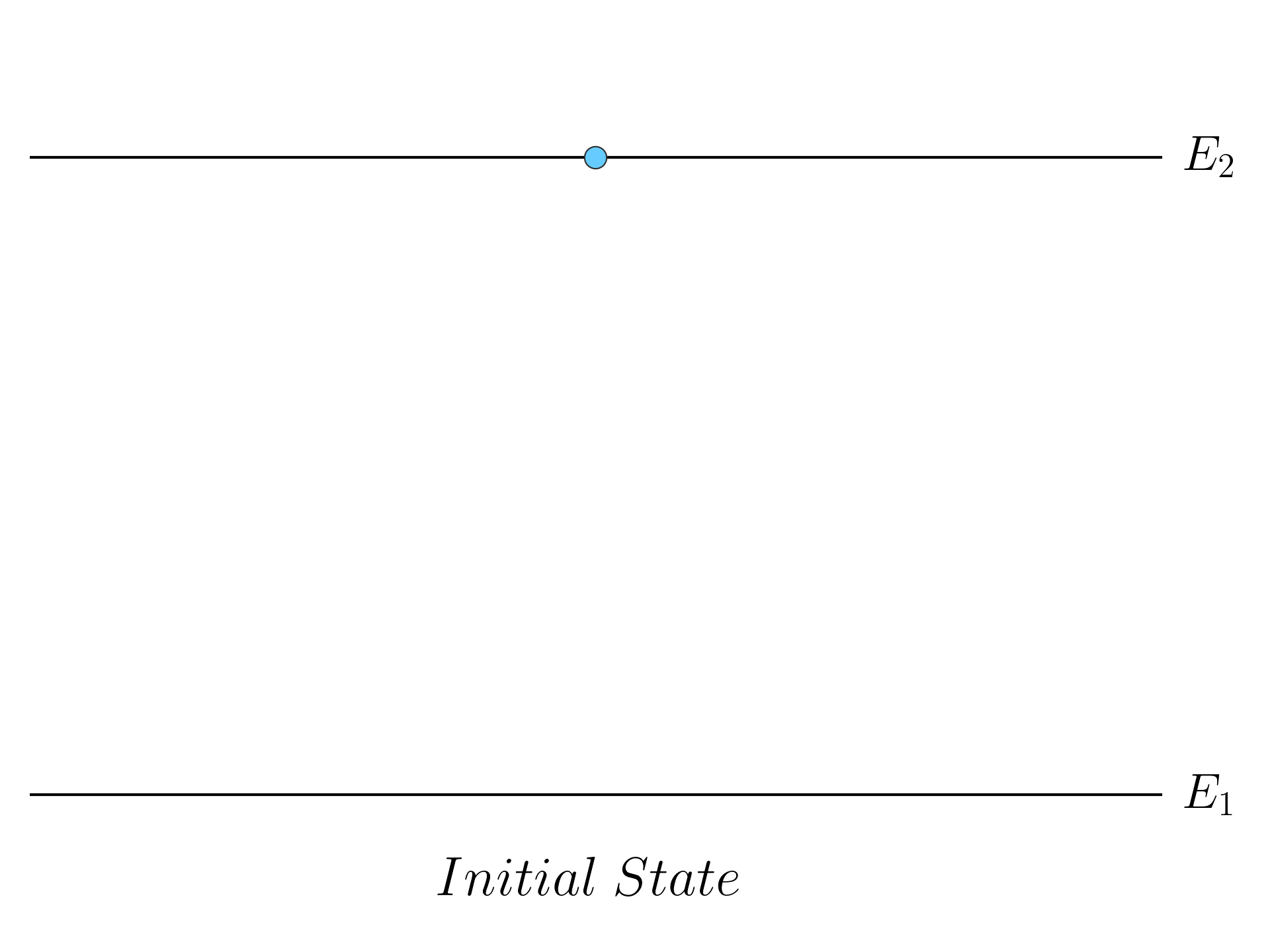
If this electron interacting with a semiclassical electromagnetic field, the electron would theoretically remain in this state indefinitely. This is because, within the semiclassical framework, the field does not possess the necessary quantum fluctuations to induce transitions between energy levels. However, if we instead use a quantized electromagnetic field, the situation changes significantly. The quantized field introduces vacuum fluctuations and the possibility of spontaneous emission, which can cause the electron to transition to a lower energy state.
This state can be written as:
| \hat \psi \rangle = \mathbf b_2^\dag | \mathbf 0 \rangle
The total energy for this state is:
E_q = E_b = E_2
The perturbing Hamiltonian multiply by the initial state is:
\begin{aligned} \mathbf H_p | \hat \psi \rangle & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k\left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \mathbf b_2^\dag | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_2^\dag \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \left(\delta_{k2} - \mathbf b_1^\dag\mathbf b_k \right) \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \mathbf b^\dag_j\left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) | \mathbf 0 \rangle \\ & = -\sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \mathbf b^\dag_j\mathbf a_\lambda^\dag | \mathbf 0 \rangle \end{aligned}
There are only one possible choices that give non-zero results (and therefore only one state that might have a non-zero perturbation theory coefficients) as any other state would be orthogonal to this state and the coefficient will be zero.
\mathbf b^\dag_j\mathbf a_\lambda^\dag | \mathbf 0 \rangle
which is the state with one electron in state | j \rangle and one photon in mode | \lambda \rangle, so a photon has been emitted; the energy for this state is:
E_r = E_b + E_f = E_j + \hbar \omega_\lambda
The coefficient for this case is:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_\lambda \mathbf b_j | \mathbf H_p | \mathbf b^\dag_j\mathbf a_\lambda^\dag | \mathbf 0 \rangle \\ & =\frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_\lambda \mathbf b_j |\left( \mathbf H_p | \mathbf b^\dag_j\mathbf a_\lambda^\dag | \mathbf 0 \rangle \right) \\ & =-\frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_\lambda \mathbf b_j |\sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \mathbf b^\dag_j\mathbf a_\lambda^\dag | \mathbf 0 \rangle \\ & =-\frac{1}{i\hbar} e^{i\omega_{rq}t} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \langle \mathbf 0 | \mathbf a_\lambda \mathbf b_j \mathbf b^\dag_j\mathbf a_\lambda^\dag | \mathbf 0 \rangle \\ & =-\frac{1}{i\hbar} e^{i\omega_{rq}t} \sum_\lambda \mathbf {\hat H}_{\lambda,j2} \end{aligned}
With the values of the problem it becomes, for a specific |\lambda \rangle:
\begin{aligned} \dot a_r^{(1)} & = -\frac{1}{i\hbar} e^{i\omega_{rq}t}\mathbf {\hat H}_{\lambda,j2} = -\frac{1}{i\hbar} e^{i\frac{E_r - E_q}{\hbar}t}\mathbf {\hat H}_{\lambda,j2} \\ & = -\frac{1}{i\hbar} e^{i\frac{E_j + \hbar \omega_\lambda - E_2}{\hbar}t} \mathbf {\hat H}_{\lambda,j2} = -\frac{1}{i\hbar} e^{i\frac{E_j + \hbar \omega_\lambda - E_2}{\hbar}t} \mathbf {\hat H}_{\lambda,j2} \end{aligned}
We can apply Fermi Golden rules and compute the transition rate:
w_r = \frac{2\pi}{\hbar}\left| \mathbf {\hat H}_{\lambda,j2} \right|^2 \delta\left(E_j - E_2 + \hbar\omega_\lambda\right)
As there are only two energy states (| 1 \rangle and | 2 \rangle), we can substitute. For | j \rangle = | 2 \rangle:
w_r = \frac{2\pi}{\hbar} \left| \mathbf {\hat H}_{1,22} \right|^2 \delta\left(E_2 - E_2 + \hbar\omega_\lambda\right) = \frac{2\pi}{\hbar} \left| \mathbf {\hat H}_{1,22} \right|^2 \delta\left(\hbar\omega_\lambda\right)
There is no energy that can make the delta unitary.
For | j \rangle = | 1 \rangle:
w_r = \frac{2\pi}{\hbar} \left| \mathbf {\hat H}_{1,12} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega_\lambda\right)
There is a finite transition rate for a specific value of \lambda for which the photon energy \hbar \omega_\lambda is equal to the difference in energies:
\hbar\omega_\lambda = E_2 - E_1
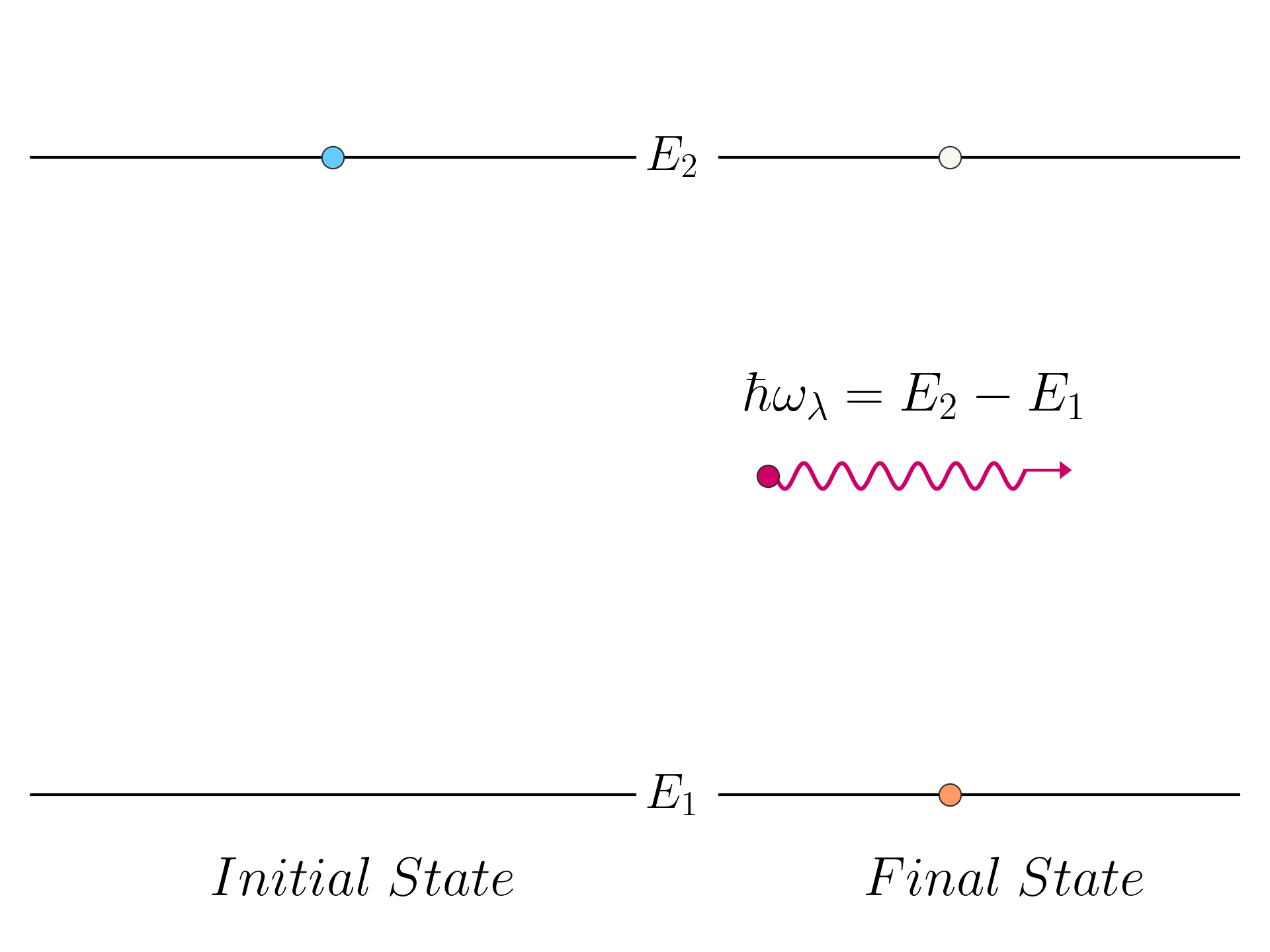
This process describe a (spontaneous) emission process, starting with one electron in state | 2 \rangle and no photon, and and ending with an electron in state | 2 \rangle and a photon which is created in mode | \lambda \rangle.
Multiple photons spontaneous emission
Let’s consider an electron in an excited state (state | 2 \rangle) and and n photons in mode |\lambda \rangle \ne | 1 \rangle. This case is equivalent of the stimulated emission below with |\lambda \rangle \ne | 1 \rangle and will be demonstrated that the transition rate is:
w_r = \frac{2\pi}{\hbar}\sum_\lambda \left| \mathbf {\hat H}_{1,12} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega_\lambda\right)
Stimulated emission
Let’s assume that there is an electron in state | 2 \rangle and a photon in mode | 1 \rangle.
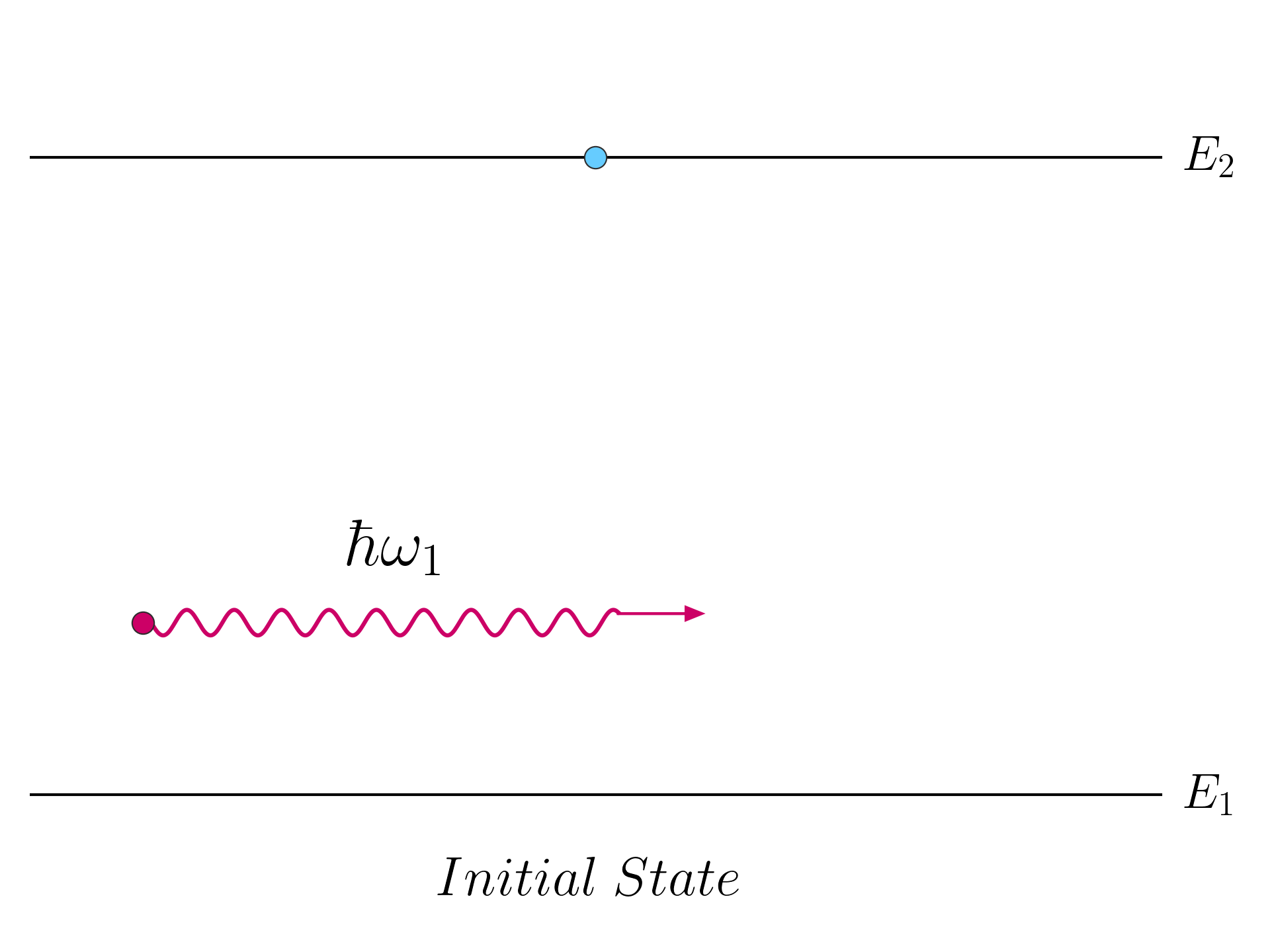
This state can be written as:
| \hat \psi \rangle = \mathbf b_2^\dag \mathbf a_1^\dag | \mathbf 0 \rangle
The total energy for this state is:
E_q = E_b + E_f = E_2 + \hbar\omega_1
The perturbing Hamiltonian multiply by the initial state is:
\begin{aligned} \mathbf H_p | \hat \psi \rangle & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k\left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \mathbf b_2^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_2^\dag \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \mathbf a_1^\dag | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_2^\dag \left(\mathbf a_\lambda \mathbf a_1^\dag - \mathbf a_\lambda^\dag\mathbf a_1^\dag\right) | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \left(\delta_{k1} - \mathbf b_2^\dag\mathbf b_k \right) \left(\delta_{\lambda1} + \mathbf a_1^\dag \mathbf a_\lambda - \mathbf a_\lambda^\dag\mathbf a_1^\dag\right) | \mathbf 0 \rangle \\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \mathbf b^\dag_j\left(\delta_{\lambda1} - \mathbf a_\lambda^\dag\mathbf a_1^\dag\right) | \mathbf 0 \rangle\\ & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \left(\delta_{k2} \delta_{\lambda1} \mathbf b^\dag_j| \mathbf 0 \rangle - \delta_{k2} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle\right) \end{aligned}
We have used standard manipulation to push the annihilation operators to the right and the commutation relation for fermions and bosons (recalling that they have a different sign).
There are only two possible choices that give non-zero results (and therefore only two state that might have a non-zero perturbation theory coefficients) as any other state would be orthogonal to these two states and the coefficient will be zero.
The first possibility is to have as final state:
\mathbf b^\dag_j| \mathbf 0 \rangle
This possibility, which corresponds to absorption, is not possible, because there is no possible state that the electron can go to (state | 2 \rangle is already occupied and there are no other upper states).
The second possibility is to have as a final state:
\mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle
To ensure proper normalization, two cases need to be considered. The first case is | \lambda \rangle \ne | 1 \rangle. In this case the state is already normalized.
The energy of this state is the sum of the energy of the electron and the energy of the two photons:
E_r = E_b + E_f = E_j + \hbar \omega_\lambda + \hbar \omega_1
The coefficient for this case is:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j | \mathbf H_p | \mathbf b_2^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \\ & =\frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j |\left( \mathbf H_p | \mathbf b_2^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j | \sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \left(\delta_{k2} \delta_{\lambda1} \mathbf b^\dag_j| \mathbf 0 \rangle - \delta_{k2} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle\right) \\ & =- \frac{1}{i\hbar} e^{i\omega_{rq}t}\langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j |\sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle \\ & = -\frac{1}{i\hbar} e^{i\omega_{rq}t}\sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle \\ & = -\frac{1}{i\hbar} e^{i\omega_{rq}t} \sum_{\lambda} \mathbf {\hat H}_{\lambda,j2} \end{aligned}
With the values of the problem it becomes, for a specific |\lambda \rangle:
\begin{aligned} \dot a_r^{(1)} & = -\frac{1}{i\hbar} e^{i\omega_{rq}t}\mathbf {\hat H}_{\lambda,j2} = -\frac{1}{i\hbar} e^{i\frac{E_r - E_q}{\hbar}t} \mathbf {\hat H}_{\lambda,j2} \\ & = -\frac{1}{i\hbar} e^{i\frac{E_j + \hbar \omega_\lambda + \hbar \omega_1 - E_2 - \hbar\omega_1}{\hbar}t} \mathbf {\hat H}_{\lambda,j2} = -\frac{1}{i\hbar} e^{i\frac{E_j + \hbar \omega_\lambda - E_2}{\hbar}t} \mathbf {\hat H}_{\lambda,j2} \end{aligned}
We can apply Fermi Golden rules and compute the transition rate:
w_r = \frac{2\pi}{\hbar} \left| \mathbf {\hat H}_{\lambda,j2} \right|^2 \delta\left(E_j - E_2 + \hbar\omega_\lambda\right)
For | j \rangle = | 2 \rangle, since \hbar \omega_\lambda > 0\, \forall \lambda there is not any combination that makes the delta function unitary, and therefore there are no physical solutions.
For | j \rangle = | 1 \rangle, the transition rate is:
w_r = \frac{2\pi}{\hbar} \left| \mathbf {\hat H}_{\lambda,12} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega_\lambda\right)
The photon energy \hbar \omega_\lambda is equal to the difference in energies:
\hbar\omega_\lambda = E_2 - E_1
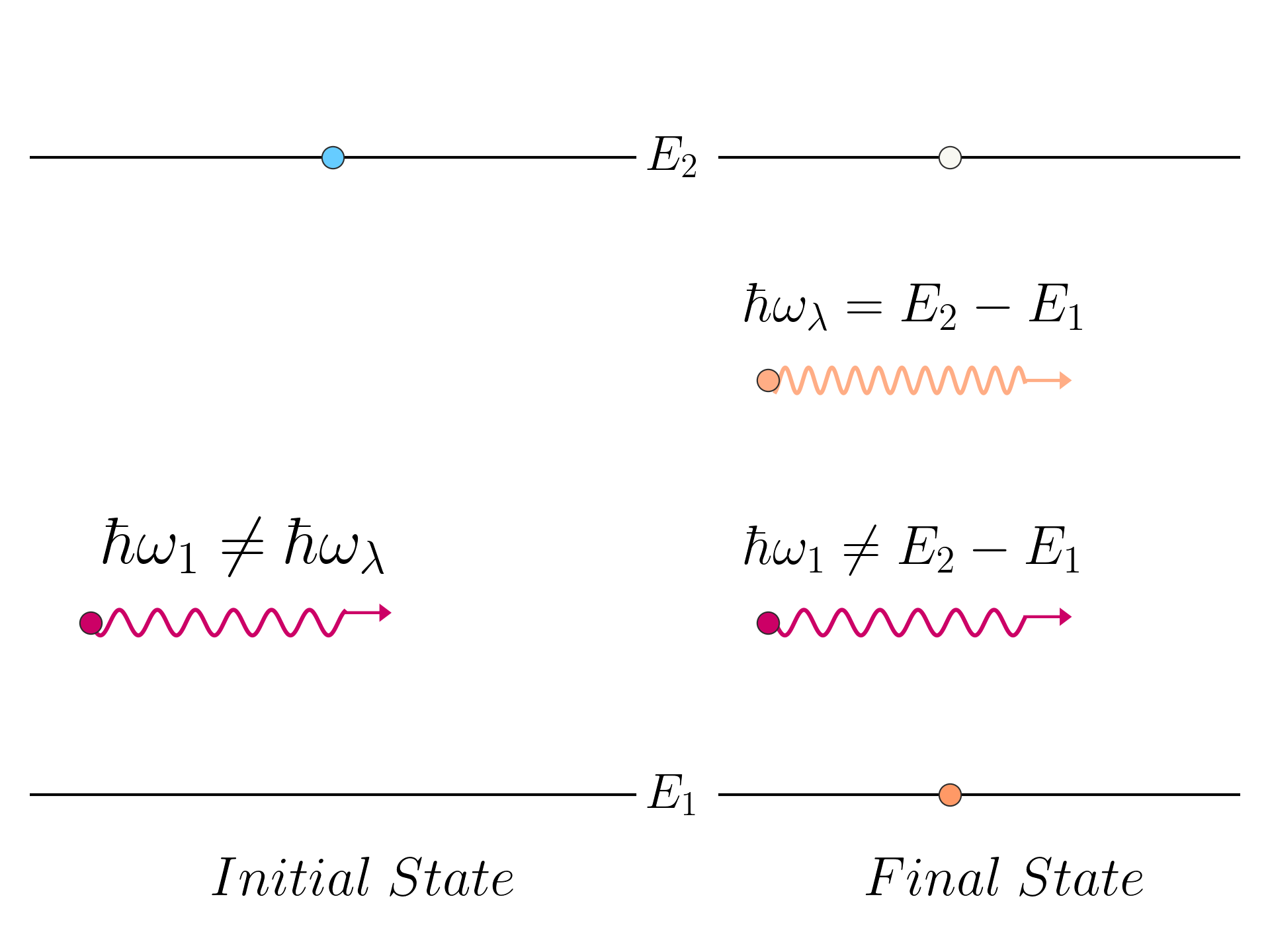
which is the case identical to the spontaneous emission, with the difference of the presence of an additional photon (or any number of additional number of photons of different mode | \lambda \rangle) which is not interacting with the electron.
The second case is | \lambda \rangle = | 1 \rangle. In this case the state is requiring a normalization:
\frac{1}{\sqrt 2}\mathbf b^\dag_j \left(\mathbf a_1^\dag \right)^2 | \mathbf 0 \rangle
The energy of this state is the sum of the energy of the electron and the energy of the two identical photons:
E_r = E_b + E_f = E_j + 2 \hbar \omega_1
The coefficient for this case is:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{1}{\sqrt 2}\langle \mathbf 0 | \mathbf b_j \left(\mathbf a_1\right)^2 | \mathbf H_p | \mathbf b_2^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \\ & =\frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{1}{\sqrt 2}\langle \mathbf 0 | \mathbf b_j \left(\mathbf a_1\right)^2 |\left( \mathbf H_p | \mathbf b_2^\dag \mathbf a_1^\dag | \mathbf 0 \rangle \right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle \mathbf 0 | \mathbf a_1 \mathbf a_\lambda \mathbf b_j | \sum_{\lambda,k} \mathbf {\hat H}_{\lambda,jk} \left(\delta_{k2} \delta_{\lambda1} \mathbf b^\dag_j| \mathbf 0 \rangle - \delta_{k2} \mathbf b^\dag_j\mathbf a_\lambda^\dag\mathbf a_1^\dag | \mathbf 0 \rangle\right) \\ & = - \frac{1}{i\hbar} e^{i\omega_{rq}t}\frac{1}{\sqrt 2}\langle \mathbf 0 | \mathbf b_j \left(\mathbf a_1\right)^2 |\sum_{k} \mathbf {\hat H}_{1,jk} \delta_{k2} \mathbf b^\dag_j\left(\mathbf a_1^\dag \right)^2 | \mathbf 0 \rangle \\ & = - \frac{\sqrt 2}{i\hbar} e^{i\omega_{rq}t}\frac{1}{\sqrt 2}\langle \mathbf 0 | \mathbf b_j \left(\mathbf a_1\right)^2 |\sum_{k} \mathbf {\hat H}_{1,jk} \delta_{k2} \frac{1}{\sqrt 2}\mathbf b^\dag_j\left(\mathbf a_1^\dag \right)^2 | \mathbf 0 \rangle \\ & = - \frac{\sqrt 2}{i\hbar} e^{i\omega_{rq}t} \sum_{k} \mathbf {\hat H}_{1,jk} \delta_{k2} \\ & = - \frac{\sqrt 2}{i\hbar} e^{i\omega_{rq}t} \mathbf {\hat H}_{1,j2} \end{aligned}
We used the fact that the product of a state with itself is 1:
\frac{1}{\sqrt 2}\langle \mathbf 0 | \mathbf b_j (\mathbf a_1)^2 \cdot \frac{1}{\sqrt 2}\mathbf b^\dag_j (\mathbf a_1^\dag )^2 | \mathbf 0 \rangle = 1
but it then require a \sqrt 2 multiplying the result.
With the values of the problem it becomes:
\begin{aligned} \dot a_r^{(1)} & = -\frac{1}{i\hbar} e^{i\omega_{rq}t}\sqrt 2 \mathbf {\hat H}_{1,j2} = -\frac{1}{i\hbar} e^{i\frac{E_r - E_q}{\hbar}t} \sqrt 2 \mathbf {\hat H}_{1,j2} \\ & = -\frac{1}{i\hbar} e^{i\frac{E_j + 2\hbar \omega_1 - E_2 - \hbar\omega_1}{\hbar}t}\sqrt 2 \mathbf {\hat H}_{1,j2} = -\frac{1}{i\hbar} e^{i\frac{E_j + \hbar \omega_1 - E_2}{\hbar}t} \sqrt 2 \mathbf {\hat H}_{1,j2} \end{aligned}
We can apply Fermi Golden rules and compute the transition rate:
w_r = \frac{2\pi}{\hbar} 2 \left| \mathbf {\hat H}_{1,j2} \right|^2 \delta\left(E_j - E_2 + \hbar\omega_1\right)
For | j \rangle = | 2 \rangle, since \hbar \omega_1 > 0\, \forall \lambda there is not any combination that makes the delta function unitary, and therefore there are no physical solutions.
For | j \rangle = | 1 \rangle, the transition rate is:
w_r = \frac{2\pi}{\hbar} 2 \left| \mathbf {\hat H}_{1,12} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega_1\right)
For a specific value of | \lambda \rangle = | 1 \rangle for which the photon energy \hbar \omega_\lambda is equal to the difference in energies:
\hbar\omega_1 = E_2 - E_1
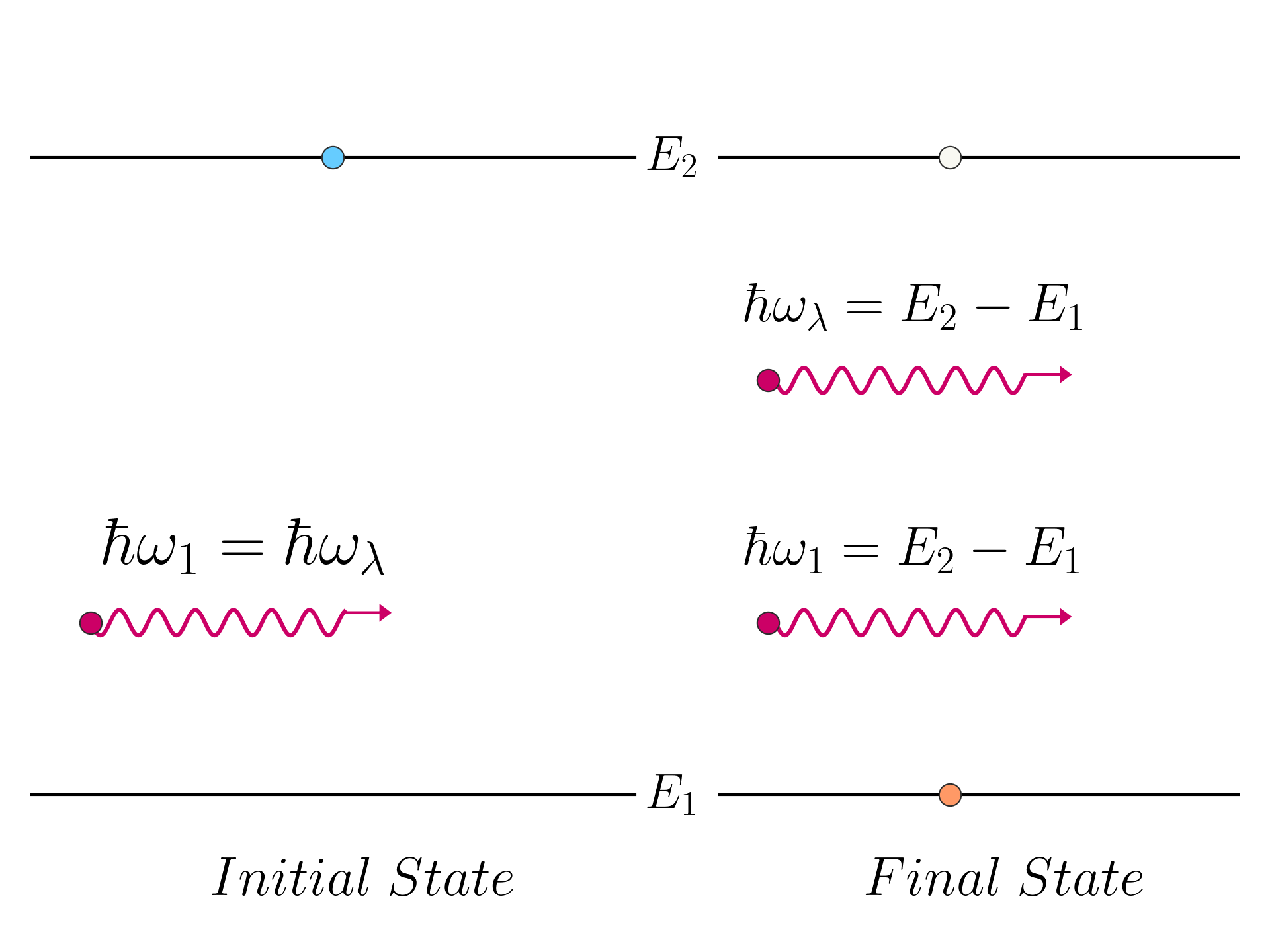
So the system start with one electron in state | 2 \rangle and one photon in mode | 1 \rangle and terminates with one electron in state | 1 \rangle and two photons in state | 1 \rangle, with the difference compared to the previous case that the transition rate is double in this case.
Multiple photons stimulated emission
Let’s assume that there is an electron in state | 2 \rangle and n photon in mode | 1 \rangle (the case |\lambda \rangle \ne | 1 \rangle has been already analyzed here.
| \hat \psi \rangle =\frac{1}{\sqrt{n!}} \mathbf b_2^\dag \left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle
The total energy for this state is:
E_q = E_b + E_f = E_2 + n\hbar\omega_1
The perturbing Hamiltonian multiply by the initial state is:
\begin{aligned} \mathbf H_p | \hat \psi \rangle & = \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k\left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \frac{1}{\sqrt{n!}} \mathbf b_2^\dag\left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_2^\dag \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right)\left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \mathbf b_k \mathbf b_2^\dag \left[\mathbf a_\lambda \left(\mathbf a_1^\dag \right)^n - \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n\right] | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \mathbf b^\dag_j \left(\delta_{k2} - \mathbf b_2^\dag\mathbf b_k \right) \left(n \delta_{\lambda 1} \left(\mathbf{a}_1^\dag\right)^{n-1} + \left(\mathbf{a}_1^\dag\right)^n \mathbf{a}_\lambda - \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n\right) | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \delta_{k2} \mathbf b^\dag_j \left(n \delta_{\lambda 1} \left(\mathbf{a}_1^\dag\right)^{n-1} - \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n\right) | \mathbf 0 \rangle \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j,k} \mathbf {\hat H}_{\lambda,jk} \left(n \delta_{k2} \delta_{\lambda 1} \mathbf b^\dag_j \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle - \delta_{k1} \mathbf b^\dag_j \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n| \mathbf 0 \rangle \right) \\ & = \frac{1}{\sqrt{n!}} \sum_{\lambda,j1} \mathbf {\hat H}_{\lambda,j2} \left(n \delta_{\lambda 1} \mathbf b^\dag_j \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle - \mathbf b^\dag_j \mathbf a_\lambda^\dag\left(\mathbf a_1^\dag \right)^n| \mathbf 0 \rangle \right) \\ & = \frac{1}{\sqrt{n!}} \mathbf {\hat H}_{1,j2} \left(n \mathbf b^\dag_j \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle - \mathbf b^\dag_j \left(\mathbf a_1^\dag \right)^{n+1}| \mathbf 0 \rangle \right) \\ \end{aligned}
The same argument can be used for the final state:
\mathbf b^\dag_j \left(\mathbf{a}_1^\dag\right)^{n-1}| \mathbf 0 \rangle
as there is no possible state that the electron can go to (state | 2 \rangle is already occupied and there are no other upper states) and | j \rangle = |1 \rangle:
\frac{1}{\sqrt{(n+1)!}}\mathbf b^\dag_1 \left(\mathbf a_1^\dag \right)^{n+1}| \mathbf 0 \rangle
The energy of this state is the sum of the energy of the electron and the energy of n identical photons:
E_r = E_b + E_f = E_1 + n \hbar \omega_1
The coefficient for this case is:
\begin{aligned} \dot a_r^{(1)} & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \langle N_{fr}; N_{br} | \mathbf H_p |N_{fq};N_{bq}\rangle \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{1}{\sqrt{(n+1)!}} \langle \mathbf 0 | \left(\mathbf a_1\right)^{n+1}\mathbf b_1 | \mathbf H_p | \frac{1}{\sqrt{n!}} \mathbf b_2^\dag \left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \\ & =\frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{1}{\sqrt{(n+1)!}}\langle \mathbf 0 |\left(\mathbf a_1\right)^{n+1}\mathbf b_1|\left( \mathbf H_p | \frac{1}{\sqrt{n!}} \mathbf b_2^\dag \left(\mathbf a_1^\dag \right)^n | \mathbf 0 \rangle \right) \\ & = \frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{1}{\sqrt{(n+1)!}}\langle \mathbf 0 | \left(\mathbf a_1\right)^{n+1}\mathbf b_1| \frac{1}{\sqrt{n!}} \mathbf {\hat H}_{1,12} - \mathbf b^\dag_1 \left(\mathbf a_1^\dag \right)^{n+1}| \mathbf 0 \rangle \\ & = -\frac{1}{i\hbar} e^{i\omega_{rq}t} \frac{\sqrt{n+1}}{\sqrt{(n+1)!}} \mathbf {\hat H}_{1,12} \frac{1}{\sqrt{(n+1)!}}\langle \mathbf 0 | \left(\mathbf a_1\right)^{n+1}\mathbf b_1|\mathbf b^\dag_1 \left(\mathbf a_1^\dag \right)^{n+1}| \mathbf 0 \rangle \\ & = -\frac{1}{i\hbar} e^{i\omega_{rq}t} \sqrt{n+1} \mathbf {\hat H}_{1,12} \frac{1}{\sqrt{(n+1)!}}\langle \mathbf 0 | \left(\mathbf a_1\right)^{n+1}\mathbf b_1| \frac{1}{\sqrt{(n+1)!}} \mathbf b^\dag_1 \left(\mathbf a_1^\dag \right)^{n+1}| \mathbf 0 \rangle \\ & = -\frac{1}{i\hbar} e^{i\omega_{rq}t} \sqrt{n+1} \mathbf {\hat H}_{1,12} \end{aligned}
With the values of the problem it becomes:
\begin{aligned} \dot a_r^{(1)} & = -\frac{1}{i\hbar} e^{i\omega_{rq}t}\sqrt {n+1} \mathbf {\hat H}_{1,12} = -\frac{1}{i\hbar} e^{i\frac{E_r - E_q}{\hbar}t} \sqrt {n+1} \mathbf {\hat H}_{1,12} \\ & = -\frac{1}{i\hbar} e^{i\frac{E_1 + (n+1)\hbar \omega_1 - E_2 - n\hbar\omega_1}{\hbar}t}\sqrt {n+1} \mathbf {\hat H}_{1,12} = -\frac{1}{i\hbar} e^{i\frac{E_1 + \hbar \omega_1 - E_2}{\hbar}t} \sqrt {n+1} \mathbf {\hat H}_{1,12} \end{aligned}
We can apply Fermi Golden rules and compute the transition rate:
w_r = \frac{2\pi}{\hbar} (n + 1) \left| \mathbf {\hat H}_{1,22} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega_1\right)
Total spontaneous emission rate
Once the spontaneous emission transition rate is computed, it is possible to sum all the possible contribution over \lambda to compute the total transition rate, noting that for a two state electrons to have an emission the electron must start in state | 2 \rangle and end in state | 1 \rangle:
W = \sum_r w_r = \frac{2\pi}{\hbar}\sum_\lambda\left| \mathbf {\hat H}_{\lambda,12} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega_\lambda\right)
From the previous derivation:
\mathbf {\hat H}_{\lambda,jk}= \int \phi_j(\mathbf r_n) \sum_{n=1}^N e i\sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf u_\lambda(\mathbf r_n) \cdot \mathbf r_n \phi_k(\mathbf r_n) \mathrm d^3 \mathbf r_n
For spontaneous emission, we typically use the electric dipole approximation where \mathbf{u}_\lambda(\mathbf{r}) \approx \mathbf{u}_\lambda (constant in space):
\mathbf{\hat{H}}_{\lambda,12} \approx e i \sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf{u}_\lambda \cdot \int \phi_2(\mathbf{r}) \mathbf{r} \phi_1(\mathbf{r}) \, \mathrm{d}^3 \mathbf{r}
The integral in the expression is the dipole matrix element \mu_{21}:
\mu_{21} = \int \phi_2(\mathbf{r}) \mathbf{r} \phi_1(\mathbf{r}) \, \mathrm{d}^3 \mathbf{r}
The integral in the expression is the dipole matrix element \mu_{21}:
\mu_{21} = \int \phi_2(\mathbf{r}) \mathbf{r} \phi_1(\mathbf{r}) \, \mathrm{d}^3 \mathbf{r}
Squaring the matrix element:
\left| \mathbf{\hat{H}}_{\lambda,12} \right|^2 = \left| e i \sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 = e^2 \frac{\hbar \omega_\lambda}{2 \varepsilon_0} \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2
Substituting in the total emission formula:
W = \frac{2\pi}{\hbar} \sum_\lambda e^2 \frac{\hbar \omega_\lambda}{2 \varepsilon_0} \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega_\lambda\right)
The sum over \lambda can be converted into an integral over the density of states \rho(\omega):
\sum_\lambda \to \int \rho(\omega) \, \mathrm{d}\omega
The formula becomes:
W = \frac{2\pi}{\hbar} \int e^2 \frac{\hbar \omega}{2 \varepsilon_0} \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 \delta\left(E_1 - E_2 + \hbar\omega\right) \rho(\omega) \, \mathrm{d}\omega
Evaluating the integral, the delta function \delta(E_1 - E_2 + \hbar\omega) will pick out \omega such that \hbar\omega = E_2 - E_1:
W = \frac{2\pi}{\hbar} e^2 \frac{\hbar (E_2 - E_1)}{2 \varepsilon_0} \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 \rho\left(\frac{E_2 - E_1}{\hbar}\right)
In free space, the density of states for photons is given by:
\rho(\omega) = \frac{\omega^2}{\pi^2 c^3}
Thus:
\rho\left(\frac{E_2 - E_1}{\hbar}\right) = \frac{\left(\frac{E_2 - E_1}{\hbar}\right)^2}{\pi^2 c^3} = \frac{(E_2 - E_1)^2}{\pi^2 \hbar^3 c^3}
Using this formula:
W = \frac{2\pi}{\hbar} e^2 \frac{\hbar (E_2 - E_1)}{2 \varepsilon_0} \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 \frac{(E_2 - E_1)^2}{\pi^2 \hbar^3 c^3}
Simplifying:
W = \frac{e^2 (E_2 - E_1)^3}{\pi \hbar^4 c^3 2 \varepsilon_0} \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2
We need to average \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 over all directions of the unit vector \mathbf{u}_\lambda. Since \mathbf{u}_\lambda is a unit vector, the average over directions and polarization gives:
\left< \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 \right> = \frac{1}{3} \left| \mu_{21} \right|^2
The final result is:
W = \frac{e^2 (E_2 - E_1)^3}{3 \pi \varepsilon_0 \hbar^4 c^3} \left| \mu_{21} \right|^2
Converting E_2 - E_1 to \hbar \omega:
W = \frac{e^2 \omega^3 \left| \mu_{21} \right|^2}{3 \pi \varepsilon_0 \hbar c^3}
Thus, we have derived the total spontaneous emission rate W as:
W = \frac{e^2 \omega^3 \left| \mu_{21} \right|^2}{3 \pi \varepsilon_0 \hbar c^3}
The natural lifetime (or spontaneous emission lifetime) \tau of an excited state in an atom or molecule is the average time that the system remains in the excited state before spontaneously emitting a photon and transitioning to a lower energy state. It is inversely related to the spontaneous emission rate W:
\tau = \frac{1}{W} = \frac{3 \pi \varepsilon_0 \hbar c^3}{e^2 \omega^3 \left| \mu_{21} \right|^2}
Average on all directions
The factor of \frac{1}{3} comes from the angular averaging of the square of the dot product between a unit vector and another vector in three-dimensional space.
Consider two vectors \mathbf{u}_\lambda and \mu_{21}, where \mathbf{u}_\lambda is a unit vector. The dot product of these vectors is given by:
\mathbf{u}_\lambda \cdot \mu_{21} = |\mathbf{u}_\lambda| |\mu_{21}| \cos \theta = |\mu_{21}| \cos \theta
where \theta is the angle between the two vectors.
When considering spontaneous emission, the direction of the unit vector \mathbf{u}_\lambda (which represents the polarization direction of the emitted photon) is equally likely in all directions. We need to average the square of the dot product over all possible directions of \mathbf{u}_\lambda.
\left< \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 \right>
Since \mathbf{u}_\lambda is a unit vector, it can point in any direction uniformly over the surface of a sphere. The expression |\mathbf{u}_\lambda \cdot \mu_{21}|^2 depends on the angle \theta, and we need to average \cos^2 \theta over all possible angles.
To average \cos^2 \theta over all directions on the unit sphere (which has a surface area in three-dimensional space of 4\pi), we integrate over the solid angle d\Omega and divide it by the total surface area:
\left< \cos^2 \theta \right> = \frac{1}{4\pi} \int_0^{2\pi} \int_0^{\pi} \cos^2 \theta \sin \theta \, \mathrm d\theta \, \mathrm d\phi
The integral over \phi is:
\int_0^{2\pi} \mathrm d\phi = 2\pi
The integral over \theta is:
\int_0^{\pi} \cos^2 \theta \sin \theta \, \mathrm d\theta
Let u = \cos \theta. Then \mathrm du = -\sin \theta \, \mathrm d\theta and the limits of integration change from \theta = 0 to \theta = \pi corresponding to u = 1 to u = -1.
\int_0^{\pi} \cos^2 \theta \sin \theta \, \mathrm d\theta = \int_1^{-1} u^2 (-\mathrm du) = \int_{-1}^{1} u^2 \, \mathrm du
Then:
\int_{-1}^{1} u^2 \, \mathrm du = \left[ \frac{u^3}{3} \right]_{-1}^{1} = \frac{1}{3} - \left( -\frac{1}{3} \right) = \frac{2}{3}
Combining the results:
\left< \cos^2 \theta \right> = \frac{1}{4\pi} \cdot 2\pi \cdot \frac{2}{3} = \frac{2}{3} \cdot \frac{1}{2} = \frac{1}{3}
Therefore, the average value of \cos^2 \theta over all directions is \frac{1}{3}.
Given that \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 = |\mu_{21}|^2 \cos^2 \theta, the average value over all possible directions of \mathbf{u}_\lambda is:
\left< \left| \mathbf{u}_\lambda \cdot \mu_{21} \right|^2 \right> = |\mu_{21}|^2 \left< \cos^2 \theta \right> = |\mu_{21}|^2 \cdot \frac{1}{3}
The factor of \frac{1}{3} comes from the spherical averaging of the square of the cosine of the angle between the unit vector and the dipole moment.
Density of states for photons
The density of states (DOS) for photons in free space represents the number of photon states per unit volume per unit frequency interval. In three-dimensional space, this can be derived considering the modes of the electromagnetic field in a cubic cavity with periodic boundary conditions.
The wave vector \mathbf{k} of a photon is related to its frequency \omega by:
\omega = c |\mathbf{k}|
where c is the speed of light in vacuum.
The number of allowed wave vectors \mathbf{k} in a cubic box of side length L with periodic boundary conditions is given by:
k_x, k_y, k_z = \frac{2\pi}{L} n_x, n_y, n_z
where n_x, n_y, n_z are integers. The volume in k-space occupied by a single state is:
\left(\frac{2\pi}{L}\right)^3 = \frac{(2\pi)^3}{L^3}
For a large box, we treat the states as continuous and the volume element in k-space is \mathrm d^3k.
The volume of a spherical shell in k-space with radius k and thickness \mathrm dk is:
\mathrm d^3k = 4\pi k^2 \mathrm dk
Using \omega = c k, we have k = \frac{\omega}{c} and dk = \frac{d\omega}{c}. Therefore:
\mathrm d^3k = 4\pi \left(\frac{\omega}{c}\right)^2 \frac{\mathrm d\omega}{c} = 4\pi \frac{\omega^2}{c^3} \mathrm d\omega
The density of states \rho(\omega) is the number of states per unit volume per unit frequency interval. Considering that each state can be occupied by two possible polarization of the photon, we multiply by 2:
\rho(\omega) \mathrm d\omega = \frac{2 \cdot \mathrm d^3k}{(2\pi)^3}
Substituting \mathrm d^3k:
\rho(\omega) \mathrm d\omega = \frac{2 \cdot 4\pi \frac{\omega^2}{c^3} \mathrm d\omega}{(2\pi)^3}
Simplifying:
\rho(\omega) = \frac{8\pi \frac{\omega^2}{c^3}}{(2\pi)^3} = \frac{\omega^2}{\pi^2 c^3}
Therefore, the density of states for photons in free space is:
\rho(\omega) = \frac{\omega^2}{\pi^2 c^3}
This expression represents the number of available photon states per unit volume per unit frequency interval for a given photon frequency \omega in free space.