Electromagnetic Field Quantization
In quantum field theory, the quantization of the electromagnetic field is a fundamental process that describes the electromagnetic field in terms of quantum mechanics. This quantization is achieved by promoting the classical field variables to operators that obey specific commutation relations. The electromagnetic field is expressed as a superposition of harmonic oscillators for each mode of the field, allowing for the description of photons, the quantum carriers of electromagnetic force, with discrete energy states. This formalism underlies the interaction of light and matter, forming the basis for technologies such as lasers and quantum computing.
The quantization of the field will be postulated, but the need for the quantization can be shown considering a plain wave and showing the necessity of quantization.
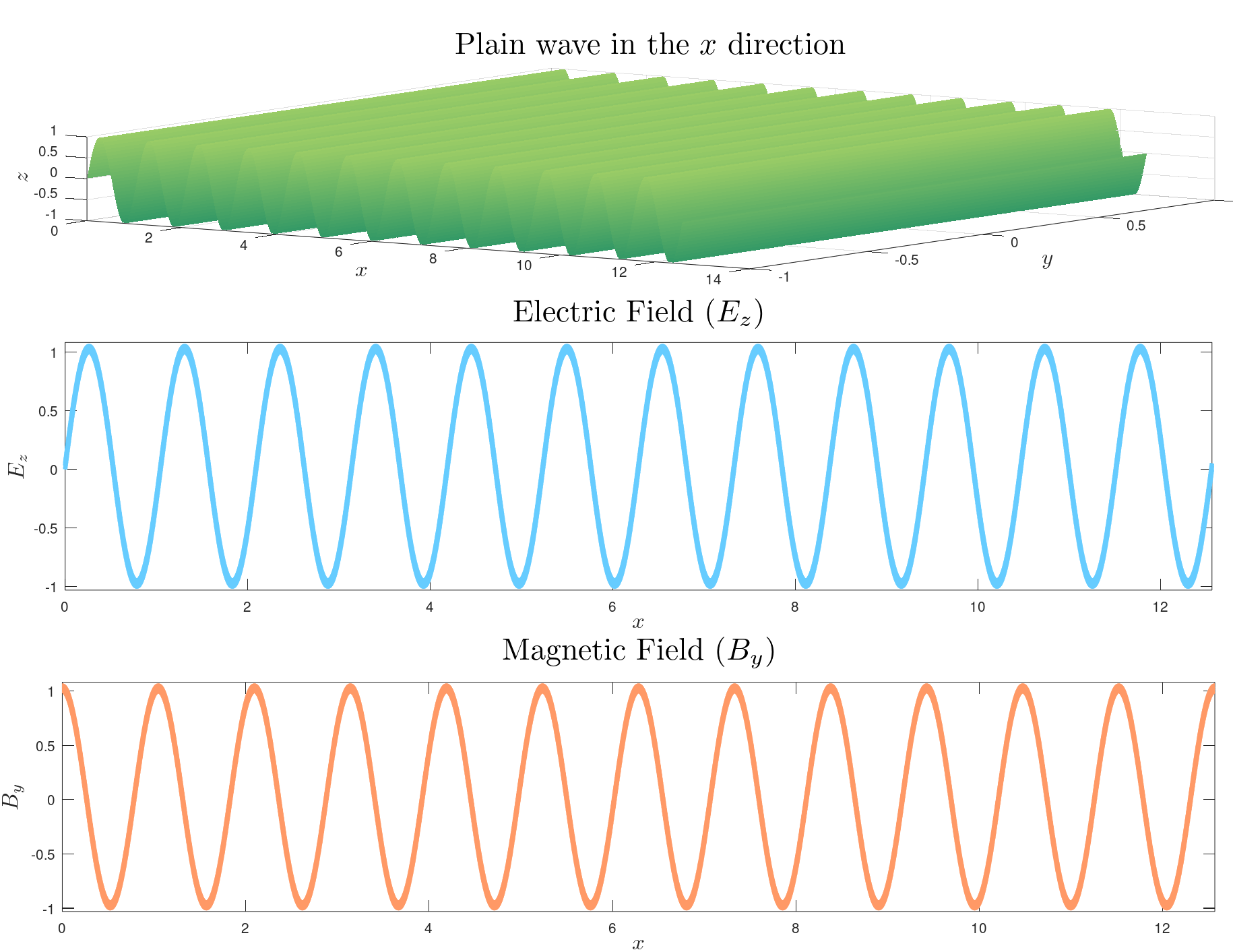
Let’s suppose to have a box of length L in the x direction, and be sufficiently large in the y and z directions to be infinite; then the description can be assimilated to a standing plain wave of some particular wavevector k.
By construction, the electric field \mathbf E and the magnetic field \mathbf B are lying on the yz plane because they are perpendicular to the direction of propagation of the wave; let’s assume that electric field is polarized in the z direction in this form:
\mathbf E = E_z \mathbf k = p(t) D \sin(kx)
Then the magnetic field being perpendicular to the electric field is polarized in the y direction:
\mathbf B = B_y \mathbf j = q(t)\frac{D}{c}\cos(kx)
with the speed of light c in the constant to simplify the equation shortly.
To see if this is an allowable field, it must satisfy Maxwell’s equations, in particular the third one:
\begin{aligned} & \nabla \times \mathbf E = -\frac{\partial \mathbf B}{\partial t} \\ & \frac{\partial E_z}{\partial x} = \frac{\mathbf B_z}{\partial t} \\ & kp D\cos(kx) = \frac{\mathrm dq}{\mathrm dt}\frac{D}{c}\cos(kx) \\ & \frac{\mathrm dq}{\mathrm dt} =kcp = \omega p \end{aligned}
and the forth one:
\begin{aligned} & \nabla \times \mathbf B = \varepsilon_0\mu_0 \frac{\partial \mathbf E}{\partial t} \\ & \frac{\partial B_y}{\partial x} = \varepsilon_0\mu_0 \frac{\mathbf E_z}{\partial t} \\ & -kq \frac{D}{c}\sin(kx) = \varepsilon_0\mu_0\frac{\mathrm dp}{\mathrm dt}D\sin(kx) \\ & \frac{\mathrm dp}{\mathrm dt} = -\frac{k}{\varepsilon_0\mu_0 c}q = -kc q = - \omega q \end{aligned}
These are the necessary conditions for satisfy Maxwell’s equations:
\begin{aligned} & \frac{\mathrm dq}{\mathrm dt} = \omega p \\ &\frac{\mathrm dp}{\mathrm dt} = - \omega q \end{aligned}
Differentiating the first equation and using second
\frac{\mathrm d^2 q}{\mathrm dt^2} = -\omega^2 q so the electromagnetic mode behave like and harmonic oscillator (here).
If we now assume that the wall at the box are perfectly reflecting then the electric field must be zero and this is a result of the physical properties of perfect conductors.
In perfect conductors, the electric field inside the material must be zero. This results from the infinite conductivity of a perfect conductor, which implies any external electric field will induce surface charges that exactly cancel the field within the material. At the interface between the vacuum (or air) and the conductor, the electric field component perpendicular to the surface must therefore also be zero to maintain this condition. This is described by the boundary condition:
E_{z}(x = 0) = E_{z}(x = L) = 0
This forces the standing wave pattern in the box, because the only way to satisfy these boundary conditions with a non-zero field solution in the region 0 < x < L is if the field configuration has nodes (points of zero amplitude) at x = 0 and x = L. In this scenario, the electric field must be quantized. Only specific wavelengths corresponding to integer multiples of half-wavelengths fit into the box, and the condition E_z(0) = E_z(L) = 0 requires that kx be a multiple of \pi at x = L, which leads to the quantization condition:
kL = n\pi
where n is a positive integer, and k is the wavenumber. This further translates to:
k = \frac{n\pi}{L}
And since the frequency \omega is related to the wavenumber by the wave equation \omega = c k (where c is the speed of light in the medium), it follows that:
\omega = \frac{n\pi c}{L}
Thus, both the wavenumber and the frequency of the wave are quantized due to the boundary conditions imposed by the walls of the box.
To find the equation describing the evolution of the field, it is possible to use Hamilton formalism if it is possible to derive an opportune set of generalized coordinates. Starting from the definition of the energy density:
W = \frac{1}{2} \left( \varepsilon_0 \mathbf E^2 + \frac{1}{\mu_0} \mathbf B^2 \right)
For the box of length L:
\begin{aligned} H & = \int_0^L W \mathrm dx = \int_0^L \frac{1}{2} \left( \varepsilon_0 E_z^2 + \frac{1}{\mu_0} B_y^2 \right) = \frac{D^2}{2} \int_0^L \left( \varepsilon_0 p^2 \sin(kx)^2 + \frac{1}{\mu_0c^2} q^2 \cos(kx)^2 \right) \mathrm dx \\ & \frac{D^2\varepsilon_0}{2} \int_0^L \left( p^2 \int_0^L \sin(kx)^2 \mathrm dx + q^2 \int_0^L \cos(kx)^2 \mathrm dx \right) \\ & \frac{D^2L\varepsilon_0}{4} \left( p^2 + q^2 \right) \end{aligned}
From the expression relating p and q previously derived, these are in Hamilton formulation with:
H = \frac{\omega}{2} \left( p^2 + q^2 \right), \quad D = \sqrt{\frac{2\omega}{L\varepsilon_0}}
Having derived the Hamiltonian, the full quantization of the electric field is done postulating to substitute the classical quantities with the quantum operators, obtaining the Hamiltonian:
\mathbf H = \frac{\omega}{2} \left( -\hbar^2\frac{\mathrm d^2}{\mathrm dq^2} + q^2 \right)
Defining a dimensionless unit:
\xi = \frac{q}{\sqrt \hbar}
the Hamiltonian becomes:
\mathbf H = \frac{\hbar\omega}{2}\left( -\frac{\mathrm d^2}{\mathrm d\xi^2} + \xi^2 \right)
Field operators
That is the same as the harmonic oscillator, in particularly the usage of the raising and lowering operators (here).
In the electromagnetic field quantization, different modes are introduced to handle the variety of electromagnetic field configurations and their respective wavelengths in the space considered. Each mode corresponds to a specific solution of Maxwell’s equations with a particular wavelength and frequency.
The use of \lambda, representing the wavelength, is essential because it allows the quantization to account for the physical properties of each mode individually. The electromagnetic spectrum consists of waves with different wavelengths, and these variations affect how the fields interact with matter and how they propagate through space.
The Hamiltonian derived for a specific mode describes the energy associated with that mode’s electromagnetic field configuration. When multiple modes are considered, the total Hamiltonian becomes a sum over all these individual mode Hamiltonians:
\mathbf H = \sum_{\lambda} \frac{1}{2} \left( |\mathbf E_{\lambda}|^2 + |\mathbf B_{\lambda}|^2 \right)
Here, \mathbf E_{\lambda} and \mathbf B_{\lambda} are the electric and magnetic fields associated with the mode of wavelength \lambda. This summation allows the system to include contributions from all relevant electromagnetic configurations, encompassing the full spectrum of possible wavelengths. This approach leads to a comprehensive description of the quantum electromagnetic field.
he nature of the incoming light affects the number of modes we might need to consider:
-
Laser Beam or Monochromatic Light: If we are dealing with a laser beam or another source of monochromatic light, we are essentially dealing with light that has a single wavelength and phase. In this scenario, it’s often sufficient to consider only a single mode in the analysis because the electromagnetic field can be described as a single sinusoidal wave at a specific frequency \omega, wavelength \lambda, and polarization. This is known as a coherent state in quantum optics.
-
Polychromatic Light: For polychromatic light, which consists of multiple wavelengths, we must consider multiple modes. Each mode corresponds to a different wavelength and potentially different directions and polarizations. This is typical for natural light or light emitted by most common light sources, which contain a broad spectrum of wavelengths.
-
Spatial Modes: Even for a monochromatic source like a laser, if the physical configuration of the system allows different spatial distributions (like different transverse modes in a laser cavity), we might still need to consider multiple modes to accurately describe the system.
For each mode the Hamiltonian can be written as:
\mathbf H_\lambda = \hbar \omega_\lambda \left(\mathbf a_\lambda ^\dag \mathbf a_\lambda + \frac{1}{2}\right)
It is possible to make usage of the creation and annihilation operators in a practical way:
\begin{aligned} & \mathbf a_\lambda | \psi_{\lambda,n} \rangle = \sqrt n_\lambda | \psi_{\lambda,n-1} \rangle \\ & \mathbf a_\lambda^\dag | \psi_{\lambda,n} \rangle = \sqrt {n_\lambda+1} | \psi_{\lambda,n+1} \rangle \end{aligned}
These quantized energy states of the electromagnetic field can be called photons and bridge the concept to the theory of light proposed by Einstein as being quantized, and therefore they annihilate or create a photon.
In addition to the already discussed quantization of the energy, and therefore that there is a discrete set of amplitudes, there are other differences compared to the classical electromagnetic fields; perhaps one of the most striking differences arises with the concept of vacuum fluctuations.
In classical electromagnetism, a vacuum (space devoid of any matter and energy) has absolutely no fields or energy present Quantum theory predicts that even in a vacuum state, where n = 0 (no photons), there are still vacuum fluctuations due to the zero-point energy \frac{1}{2}\hbar\omega of each mode. These fluctuations are not just theoretical; they have real, observable effects, such as the Casimir effect and the Lamb shift.
In parallel to quantum mechanics, when quantities are measured through operators, it is possible likewise to determine a similar sets for the electromagnetic field. Starting from the definitions of the creation and annihilation operators:
\begin{aligned} & \mathbf a_\lambda = \frac{1}{\sqrt 2} \left(\frac{\mathrm d}{\mathrm d \xi_\lambda} + \xi_\lambda\right) \\ & \mathbf a^\dag_\lambda = \frac{1}{\sqrt 2} \left(-\frac{\mathrm d}{\mathrm d \xi_\lambda} + \xi_\lambda\right) \end{aligned}
We can then rewrite the operator \xi (which is not simply a coordinate but a real operator) and define a new operator \pi as:
\begin{aligned} & \xi_\lambda = \frac{1}{\sqrt 2} \left(\mathbf a^\dag_\lambda + \mathbf a_\lambda\right) \\ & \pi_\lambda \equiv -i\frac{\mathrm d}{\mathrm d \xi_\lambda} = \frac{\mathbf p_\lambda}{\sqrt \hbar} = \frac{1}{\sqrt 2} \left(\mathbf a^\dag_\lambda - \mathbf a^\dag\right) \end{aligned}
Using these definitions into the definition of the electric and magnetic field we have two operators (note that operator \mathbf E_{\lambda,z} is not the field \mathbf E_{z}, it is just the way they are written which is similar):
\begin{aligned} & \mathbf E_{\lambda,z} = p_\lambda D \sin(kx) = \pi_\lambda \sqrt \hbar \sqrt{\frac{2\omega_\lambda}{L\varepsilon_0}} \sin(kx) = i\left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) \sqrt{\frac{\hbar\omega_\lambda}{L\varepsilon_0}} \sin(kx)\\ & \mathbf B_{\lambda,y} = p_\lambda \frac{D}{c} \cos(kx) = \xi_\lambda \sqrt \hbar \sqrt{\frac{2\omega_\lambda}{L\varepsilon_0c^2}} \cos(kx) = \left(\mathbf a^\dag_\lambda + \mathbf a_\lambda\right) \sqrt{\frac{\hbar\omega_\lambda\mu_0}{L}} \cos(kx)\\ \end{aligned}
This description of operators (which is an example of quantum field theory) allows to know the average value of a measurable quantity taking the expected value of the operator with a state | \phi \rangle of the particular mode:
\begin{aligned} & \langle \mathbf E_{\lambda,z} \rangle = \langle \phi |\mathbf E_{\lambda,z} | \phi \rangle \\ & \langle \mathbf B_{\lambda,y} \rangle = \langle \phi |\mathbf B_{\lambda,y} | \phi \rangle \end{aligned}
It is possible to compute the commutator and shows that it does not commute:
\begin{aligned} \left[\mathbf E_{\lambda,z}, \mathbf B_{\lambda,y}\right] &=i\sqrt{\frac{\mu_0}{\varepsilon_0}} \frac{\hbar\omega_\lambda}{L} \sin(kx)\cos(kx) \left[\mathbf a^\dag_\lambda - \mathbf a_\lambda, \mathbf a^\dag_\lambda + \mathbf a_\lambda\right]\\ & = -2i\sqrt{\frac{\mu_0}{\varepsilon_0}} \frac{\hbar\omega_\lambda}{L} \sin(kx)\cos(kx) \end{aligned}
as:
\begin{aligned} \left[\mathbf a^\dag_\lambda - \mathbf a_\lambda, \mathbf a^\dag_\lambda + \mathbf a_\lambda\right] & = \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right)\left(\mathbf a^\dag_\lambda + \mathbf a_\lambda\right) - \left(\mathbf a^\dag_\lambda + \mathbf a_\lambda\right)\left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) \\ & = \left(\mathbf a^\dag_\lambda\right)^2 + \mathbf a^\dag_\lambda\mathbf a_\lambda - \mathbf a_\lambda\mathbf a^\dag_\lambda - \mathbf a_\lambda^2 + \left(\mathbf a^\dag_\lambda\right)^2 - \mathbf a_\lambda\mathbf a^\dag_\lambda + \mathbf a^\dag_\lambda\mathbf a + \mathbf a_\lambda^2\\ & = \mathbf a^\dag_\lambda\mathbf a_\lambda - \mathbf a_\lambda\mathbf a^\dag_\lambda - \mathbf a_\lambda\mathbf a^\dag_\lambda + \mathbf a^\dag_\lambda\mathbf a_\lambda \\ & = 2\left(\mathbf a^\dag_\lambda\mathbf a_\lambda - \mathbf a_\lambda\mathbf a^\dag_\lambda\right) \\ & = -2\left(\mathbf a_\lambda\mathbf a^\dag_\lambda - \mathbf a^\dag_\lambda\mathbf a_\lambda\right) \\ & = -2 \end{aligned}
Since they do not commute, it is impossible by the Heisenberg uncertainty principle to know at the same time the electric and magnetic field, and they have an uncertainty:
\Delta E_{\lambda,z} \Delta B_{\lambda,y} \ge \frac{|\left[\mathbf E_{\lambda,z}, \mathbf B_{\lambda,y}\right]|}{2} = \sqrt{\frac{\mu_0}{\varepsilon_0}} \frac{\hbar\omega_\lambda}{L} \sin(kx)\cos(kx)
Time dependent solutions
The extension to time dependence is done in a similar way compared to quantum mechanics; starting from the time-independent equation:
\mathbf H | \phi \rangle = E | \phi \rangle
The postulate is to replace this equation with:
\mathbf H | \phi \rangle = i \hbar \frac{\partial}{\partial t} | \phi \rangle
and this postulation seems to work; so, if an eigensolution is known, to get the time variation of a given state it is sufficient to multiply it by:
e^{-i\frac{E}{\hbar}t}
to get a solution for the time-dependent case.
Number state
Considering a state in which there are n_\lambda photons in the mode (these are known as Fock states).
In these mode, the dimensionless quantity \xi does not have any spatial connotation, but represent the amplitude of the magnetic field (\xi = \frac{q}{\hbar}), so the probability density is the probability of finding a particular amplitude. For the electric field:
\begin{aligned} \langle n_\lambda | \mathbf E_{\lambda_,z}| n_\lambda \rangle & = \langle n_\lambda | i\left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) \sqrt{\frac{\hbar\omega_\lambda}{L\varepsilon_0}} \sin(kx)| n_\lambda \rangle \\ & = i\sqrt{\frac{\hbar\omega_\lambda}{L\varepsilon_0}} \sin(kx) \left(\langle n_\lambda | \mathbf a^\dag_\lambda - \mathbf a_\lambda | n_\lambda \rangle\right) \\ & = i\sqrt{\frac{\hbar\omega_\lambda}{L\varepsilon_0}} \sin(kx) \left(\sqrt{n+1}\langle n_{\lambda+1} | n_\lambda \rangle - \sqrt{n-1}\langle n_{\lambda-1} | n_\lambda \rangle \right) \\ & = 0 \end{aligned}
As the states are orthogonal since they are eigenstates of the same Hamiltonian. The same is true for the magnetic field:
\begin{aligned} \langle n_\lambda | \mathbf B_{\lambda_,y}| n_\lambda \rangle & = \langle n_\lambda | \left(\mathbf a^\dag_\lambda + \mathbf a_\lambda\right) \sqrt{\frac{\hbar\omega_\lambda\mu_0}{L}} \cos(kx) | n_\lambda \rangle \\ & = \sqrt{\frac{\hbar\omega_\lambda\mu_0}{L}} \cos(kx) \left(\langle n_\lambda | \mathbf a^\dag_\lambda + \mathbf a_\lambda | n_\lambda \rangle\right) \\ & = \sqrt{\frac{\hbar\omega_\lambda\mu_0}{L}} \cos(kx) \left(\sqrt{n+1}\langle n_{\lambda+1} | n_\lambda \rangle + \sqrt{n-1}\langle n_{\lambda-1} | n_\lambda \rangle \right) \\ & = 0 \end{aligned}
The expectation values of the field operators being zero suggests that the quantum state has no net electric or magnetic fields at any point. However, this doesn’t imply the absence of field effects entirely. Instead, it highlights the role of quantum fluctuations around these zero mean values. To analyze the nature of these fluctuations, we examine the second-order moments (variances) of the field operators.
For the electric field variance, we have:
\begin{aligned} \langle n_\lambda | (\mathbf E_{\lambda,z})^2 | n_\lambda \rangle & = \left(\frac{\hbar\omega_\lambda}{L\varepsilon_0}\right) \sin^2(kx) \langle n_\lambda | (\mathbf a^\dag_\lambda - \mathbf a_\lambda)^2 | n_\lambda \rangle \\ & = \left(\frac{\hbar\omega_\lambda}{L\varepsilon_0}\right) \sin^2(kx) \left( \langle n_\lambda | \mathbf a^\dag_\lambda \mathbf a^\dag_\lambda - \mathbf a^\dag_\lambda \mathbf a_\lambda - \mathbf a_\lambda \mathbf a^\dag_\lambda + \mathbf a_\lambda \mathbf a_\lambda | n_\lambda \rangle \right) \\ & = \left(\frac{\hbar\omega_\lambda}{L\varepsilon_0}\right) \sin^2(kx) \left(2n + 1\right). \end{aligned}
This expression reflects the nonzero quantum fluctuations of the electric field even though its expectation value is zero. The factor (2n+1) indicates that the fluctuations increase with photon number n.
Similarly, the magnetic field variance can be calculated as:
\begin{aligned} \langle n_\lambda | (\mathbf B_{\lambda,y})^2 | n_\lambda \rangle & = \left(\frac{\hbar\omega_\lambda\mu_0}{L}\right) \cos^2(kx) \langle n_\lambda | (\mathbf a^\dag_\lambda + \mathbf a_\lambda)^2 | n_\lambda \rangle \\ & = \left(\frac{\hbar\omega_\lambda\mu_0}{L}\right) \cos^2(kx) \left(2n + 1\right). \end{aligned}
These results indicate that the quantum fluctuations are symmetric with respect to the Fock state photon number and increase with increasing photon number.
While the direct physical fields (electric and magnetic) have zero expectation values in Fock states, these states exhibit nonzero fluctuations in these fields. The fluctuations depend on both the quantum state (photon number n) and the spatial position within the wave mode (as indicated by \sin(kx) and \cos(kx) for electric and magnetic fields, respectively). This suggests that Fock states are not completely void of physical phenomena but instead are characterized by significant quantum uncertainty in their field amplitudes, central to many quantum optics experiments and technologies like quantum cryptography and computing.
Set of modes
We’ve initially focused on a single plane wave mode of the electromagnetic field, which doesn’t fully represent all possible electromagnetic fields. However, by considering multiple modes, any field can be described. Classically, electromagnetic waves can be decomposed into a superposition of modes that solve classical eigenproblems in various settings such as resonators or free space. Similar to quantum mechanics, these mode sets form a complete basis for classical wave problems.
To quantize a more general electromagnetic field, we first solve the classical modes for a specific scenario and after identifying these classical modes, we quantize each mode using previously discussed methods. This leads to a quantum description of the total field in terms of annihilation and creation operators for each mode. The quantum mechanical formulation begins with the solution to the classical mode problem, assuming a set of classical modes for the electromagnetic field, and the solution will have a form as:
\begin{aligned} & \mathbf E_\lambda(\mathbf r, \lambda) = -p_\lambda(t) D_\lambda \mathbf u_\lambda(\mathbf r) \\ & \mathbf B_\lambda(\mathbf r, \lambda) = q_\lambda(t) \frac{D_\lambda}{c} \mathbf v_\lambda(\mathbf r) \end{aligned} The previous example is a particular case of this formulation with the fields polarized in the z and y directions.
There is the further assumption \nabla \times \mathbf{u}_\lambda(\mathbf r) = k_\lambda \mathbf{v}_\lambda(\mathbf r) and \nabla \times \mathbf{v}_\lambda(\mathbf r) = k_\lambda \mathbf{u}_\lambda(\mathbf r) which is often used in electromagnetic theory to describe the relationship between orthogonal vector fields, particularly when those fields are harmonic or wave-like. As before we define \omega_\lambda = k_\lambda c.
This form is consistent with the conditions required for the fields to represent electromagnetic waves, where \mathbf{E} and \mathbf{B} fields are orthogonal to each other and to the direction of wave propagation, and they satisfy wave equations. Applying the first Maxwell equations:
\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} Apply the curl to \mathbf{E}_\lambda:
\nabla \times \mathbf{E}_\lambda = \nabla \times (-p_\lambda(t) D_\lambda \mathbf{u}_\lambda)(\mathbf r) = -p_\lambda D_\lambda (\nabla \times \mathbf{u}_\lambda)(\mathbf r)
Given the definition of \mathbf{B}_\lambda, compute its time derivative:
\frac{\partial \mathbf{B}_\lambda}{\partial t} = \frac{\partial}{\partial t} \left( q_\lambda(t) \frac{D_\lambda}{c} \mathbf{v}_\lambda(\mathbf{r}) \right) = \frac{D_\lambda}{c} \frac{\mathrm dq_\lambda}{\mathrm dt} \mathbf{v}_\lambda(\mathbf r)
Simplifying and equating:
p_\lambda D_\lambda (\nabla \times \mathbf{u}_\lambda(\mathbf r)) = \frac{D_\lambda}{c} \frac{\mathrm dq_\lambda}{\mathrm dt} \mathbf{v}_\lambda(\mathbf r)
Using the relationship previously assumed:
\nabla \times \mathbf{u}_\lambda(\mathbf r) = k_\lambda \mathbf{v}_\lambda(\mathbf r) gives:
p_\lambda (\nabla \times \mathbf{u}_\lambda(\mathbf r)) = k_\lambda \mathbf v_\lambda(\mathbf r) = \frac{1}{c}\frac{dq_\lambda}{dt} \mathbf{v}_\lambda(\mathbf r)
as \mathbf v_\lambda(\mathbf r) \ne \mathbf 0:
\frac{\mathrm dq_\lambda}{\mathrm dt} = k_\lambda c p_\lambda = \omega_\lambda p
Substituting:
p_\lambda (\nabla \times \mathbf{u}_\lambda(\mathbf r)) = \frac{\omega_\lambda}{c} p_\lambda \mathbf{v}_\lambda(\mathbf r)
Divide through by p_\lambda (assuming p_\lambda \neq 0):
\nabla \times \mathbf{u}_\lambda(\mathbf r) = \frac{\omega_\lambda}{c} \mathbf{v}_\lambda(\mathbf r)
Moving to the magnetic field and applying the third Maxwell’s equation:
\nabla \times \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} Now apply the curl to \mathbf{B}_\lambda:
\nabla \times \mathbf{B}_\lambda = \nabla \times \left(q_\lambda(t) \frac{D_\lambda}{c} \mathbf{v}_\lambda(\mathbf{r})\right) = q_\lambda \frac{D_\lambda}{c} (\nabla \times \mathbf{v}_\lambda(\mathbf r))
Given the definition of \mathbf{E}_\lambda, compute its time derivative:
\frac{\partial \mathbf{E}_\lambda}{\partial t} = \frac{\partial}{\partial t}(-p_\lambda(t) D_\lambda \mathbf{u}_\lambda(\mathbf r)) = -D_\lambda \frac{\mathrm dp_\lambda}{\mathrm dt} \mathbf{u}_\lambda(\mathbf r)
Simplifying and equating:
q_\lambda \frac{D_\lambda}{c} (\nabla \times \mathbf{v}_\lambda(\mathbf r)) = -D_\lambda \mu_0 \epsilon_0 \frac{\mathrm dp_\lambda}{\mathrm dt} \mathbf{u}_\lambda(\mathbf r) = -\frac{D_\lambda}{c^2} \frac{\mathrm dp_\lambda}{\mathrm dt} \mathbf{u}_\lambda(\mathbf r)
Using the relationship previously assumed:
\nabla \times \mathbf{v}_\lambda(\mathbf r) = k_\lambda \mathbf{u}_\lambda(\mathbf r)
gives:
q_\lambda \frac{1}{c} (\nabla \times \mathbf{v}_\lambda(\mathbf r)) = q_\lambda \frac{k_\lambda}{c} \mathbf{u}_\lambda(\mathbf r) = -\frac{1}{c^2} \frac{\mathrm dp_\lambda}{\mathrm dt} \mathbf{u}_\lambda(\mathbf r)
as \mathbf u_\lambda(\mathbf r) \ne \mathbf 0:
\frac{\mathrm dp_\lambda}{\mathrm dt} = -k_\lambda c q_\lambda = -\omega_\lambda q_\lambda
Substituting:
q_\lambda (\nabla \times \mathbf{v}_\lambda(\mathbf r)) = \frac{\omega_\lambda}{c}q_\lambda \mathbf{u}_\lambda(\mathbf r)
Dividing through by q_\lambda (assuming q_\lambda(t) \neq 0):
\nabla \times \mathbf{v}_\lambda(\mathbf r) = \frac{\omega_\lambda}{c}q_\lambda \mathbf{u}_\lambda(\mathbf r)
Summarizing, in free space (and with some extension in other situation, these satisfy the Maxwell’s equations if:
\begin{aligned} & \nabla \times \mathbf u_\lambda(\mathbf r) = \frac{\omega_\lambda}{c}\mathbf v_\lambda(\mathbf r) \\ & \nabla \times \mathbf v_\lambda(\mathbf r) = \frac{\omega_\lambda}{c}\mathbf u_\lambda(\mathbf r) \\ & \frac{\mathrm dq_\lambda}{\mathrm dt} = \omega_\lambda p_\lambda \\ & \frac{\mathrm dp_\lambda}{\mathrm dt} = \omega_\lambda q_\lambda \end{aligned}
We will presume that the spatial functions are normalized and orthogonal (which is the case for example for system where we can apply the classical Hamiltonian for the electromagnetic field).
Then, the system is in a superposition of modes:
\begin{aligned} & \mathbf E(\mathbf r, t) = \sum_\lambda -p_\lambda(t) D_\lambda \mathbf u_\lambda(\mathbf r) \\ & \mathbf B_\lambda(\mathbf r, \lambda) = \sum_\lambda q_\lambda(t) \frac{D_\lambda}{c} \mathbf v_\lambda(\mathbf r) \end{aligned}
In this case too using a similar energy density we can compute the Hamiltonian:
\begin{aligned} \mathbf H & = \int_V \mathbf W \mathrm d\mathbf r^3 = \int_V \frac{1}{2} \left( \varepsilon_0 \mathbf E^2 + \frac{1}{\mu_0} \mathbf B ^2 \right)d\mathbf r^3 \\ & \int_V \frac{\varepsilon_0}{2} \left[ \left(\sum_\lambda p_\lambda(t) D_\lambda \mathbf u_\lambda(\mathbf r)\right)^2 + \left( \sum_\lambda q_\lambda(t) D_\lambda \mathbf v_\lambda(\mathbf r)\right)^2 \right] d\mathbf r^3 \\ & \int_V \frac{\varepsilon_0}{2} \left( \sum_{\lambda_1,\lambda_2} p_{\lambda_1}(t) D_{\lambda_1} \mathbf v_{\lambda_1}(\mathbf r) p_{\lambda_2}(t) D_{\lambda_2} \mathbf v_{\lambda_2}(\mathbf r) + \sum_{\lambda_1,\lambda_2} q_{\lambda_1}(t) D_{\lambda_1} \mathbf v_{\lambda_1}(\mathbf r) q_{\lambda_2}(t) D_{\lambda_2} \mathbf v_{\lambda_2}(\mathbf r) \right) d\mathbf r^3 \\ & \frac{\varepsilon_0}{2} \sum_{\lambda} D_{\lambda}^2 \int_V \left( p_{\lambda}^2 \mathbf v_{\lambda}(\mathbf r)^2 + q_{\lambda_2}^2 \mathbf v_{\lambda}(\mathbf r)^2 \right) d\mathbf r^3 \\ & \frac{\varepsilon_0}{2} \sum_{\lambda} D_{\lambda}^2 \left( p_{\lambda}^2 \int_V \mathbf v_{\lambda}(\mathbf r)^2 d\mathbf r^3 + q_{\lambda_2}^2 \int_V \mathbf v_{\lambda}(\mathbf r)^2 d\mathbf r^3 \right) \\ & \frac{\varepsilon_0}{2} \sum_{\lambda} D_{\lambda}^2 \left( p_{\lambda}^2 + q_{\lambda_2}^2 \right) \\ \end{aligned}
This result is obtained as the functions are orthogonal and normalized. In this formulation, then this total energy is a sum of separated Hamiltonian:
\mathbf H = \sum_\lambda \mathbf H_\lambda
So it is possible to quantize it and apply to each one the same formalism previously derived, choosing D_\lambda = \sqrt{\frac{\omega_\lambda}{\varepsilon_0}} and dimensionless quantities \propto \frac{1}{\sqrt{\hbar}}:
\mathbf H = \sum_\lambda \mathbf H_\lambda = \sum_\lambda \frac{\hbar\omega_\lambda}{2}\left( -\frac{\mathrm d^2}{\mathrm d\xi_\lambda^2} + \xi_\lambda^2 \right) = \sum_\lambda \hbar \omega_\lambda \left(\mathbf a_\lambda ^\dag \mathbf a_\lambda + \frac{1}{2}\right)
The occupation number representation is a way of specifying the quantum state of a field by counting the number of photons in each of these modes.
For the photon field, the occupation number n_k specifies the number of photons in a mode with wave vector \mathbf{k} and polarization \lambda. The quantum state of the field can be described by a product over all such modes, each represented by a number state |n_k\rangle.
The creation and annihilator operator are acting on specific mode:
\begin{aligned} & \mathbf a_\lambda | \dots, n_\lambda, \dots \rangle = \sqrt{n_\lambda} | \dots, \left(n_\lambda -1\right)_\lambda, \dots \rangle \\ & \mathbf a_\lambda^\dag | \dots, n_\lambda, \dots \rangle = \sqrt{n_\lambda+1} | \dots, \left(n_\lambda +1\right)_\lambda, \dots \rangle \\ & \mathbf N_\lambda = a_\lambda^\dag a_\lambda \end{aligned}
For boson, since it is indifferent the order in which the particle are created, it means that the operations commute, and similarly mixing it unless the case when i = j for which the commutator is unitary:
\begin{aligned} & \left[ \mathbf a_i, \mathbf a_j \right] = 0 \\ & \left[ \mathbf a_i^\dag, \mathbf a_j^\dag \right] = 0 \\ & \left[ \mathbf a_i, \mathbf a_j^\dag \right] = \delta_{ij} \\ \end{aligned}
With these, it is possible to construct the full operator for the electric field (in this case too \mathbf E is the operator not the vector field) starting from the classical definition and using the quantized operator \mathbf p_\lambda:
\mathbf E(\mathbf r, t) = \sum_\lambda -p_\lambda D_\lambda \mathbf u_\lambda(\mathbf r) = i\sum_\lambda \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \sqrt{\frac{\hbar \omega_\lambda}{2 \varepsilon_0}} \mathbf u_\lambda(\mathbf r)
Similarly for the magnetic field, starting from the classical definition and using the quantized operator \mathbf q_\lambda:
\mathbf B_\lambda(\mathbf r, \lambda) = \sum_\lambda q_\lambda \frac{D_\lambda}{c} \mathbf v_\lambda(\mathbf r) = \sum_\lambda \left(\mathbf a_\lambda + \mathbf a_\lambda^\dag\right) \sqrt{\frac{\hbar \omega_\lambda\mu_0}{2}} \mathbf u_\lambda(\mathbf r)
Examples
Let’s suppose to have a box of length L in the x direction, and be sufficiently large in the y and z directions to be infinite; then the description can be assimilated to a standing plain wave of some particular wavevector k.
The electric field operator for a mode \lambda is given by (note the sign minus compared to the multi-mode formula):
\mathbf E_{\lambda,z} = i\left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) \sqrt{\frac{\hbar\omega_\lambda}{L\varepsilon_0}} \sin(kx)
Considering mode 1 (then k_n=\frac{n\pi}{L} = \frac{\pi}{L} and \omega_n = \frac{n\pi c}{L}) and the system to be in an equal superposition of 0 photons and 1 photon:
| \Psi \rangle = \frac{1}{\sqrt 2}\left(e^{-i\frac{1}{2}\omega_1t} | 0\rangle + e^{-i\frac{3}{2}\omega_1t} | 1\rangle \right)
Computing the energy expectation \langle \mathbf E_{\lambda,z} \rangle:
\begin{aligned} \langle \Psi | \mathbf E_{\lambda,z} | \Psi \rangle= & \frac{1}{\sqrt 2}\left(e^{i\frac{1}{2}\omega_1t} \langle 0 | + e^{i\frac{3}{2}\omega_1t} \langle 0 | \mathbf a \right) i\left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) \\ & \sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}} \sin\left(\frac{\pi}{L}x\right) \frac{1}{\sqrt 2}\left(e^{-i\frac{1}{2}\omega_1t} | 0\rangle + e^{-i\frac{3}{2}\omega_1t} | 1\rangle \right) \end{aligned}
For compactness, defining a few variable:
\begin{aligned} & \alpha_1 = e^{-i\frac{1}{2}\omega_1t} \\ & |\alpha_1|^2 = 1 \\ & \alpha_2 = e^{-i\frac{3}{2}\omega_1t} \\ & |\alpha_2|^2 = 1 \\ & \beta = \frac{i}{2}\sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}} \sin\left(\frac{\pi}{L}x\right) \end{aligned}
The expectation becomes:
\begin{aligned} \langle \Psi | \mathbf E_{\lambda,z} | \Psi \rangle = & \beta \left(\bar \alpha_1 \langle 0 | + \bar \alpha_2 \langle 1 | \right) \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) \left(\alpha_1 | 0\rangle + \alpha_2 | 1\rangle \right) \\ = & \beta \left(|\alpha_1|^2 \langle 0 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 0\rangle + \bar \alpha_1\alpha_2 \langle 0 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right)| 1\rangle \right. \\ & \left. + \bar \alpha_2 \alpha_1 \langle 1 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 0\rangle + |\alpha_2|^2 \langle 1 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 1\rangle \right) \end{aligned} The term with the same mode are zero:
\begin{aligned} & \langle 0 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 0\rangle = \langle 0 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 0\rangle = \left(\langle 0 |\mathbf a^\dag_\lambda \right) | 0\rangle - \langle 0 | \left(\mathbf a_\lambda| 0\rangle\right) = 0 - \langle 0 | 1 \rangle = 0 \\ & \langle 1 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 1\rangle = \langle 1 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 1\rangle = \left(\langle 1 |\mathbf a^\dag_\lambda \right) | 1\rangle - \langle 1 | \left(\mathbf a_\lambda| 1\rangle\right) = \langle 0 | 1 \rangle - \langle 1 | 2 \rangle = 0 \\ \end{aligned}
The term with a mixed mode are not zero:
\begin{aligned} & \langle 0 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 1\rangle = \langle 0 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 1\rangle = \left(\langle 0 |\mathbf a^\dag_\lambda \right) | 0\rangle - \langle 0 | \left(\mathbf a_\lambda| 1\rangle\right) = 0 - \langle 0 | 0 \rangle = -1 \\ & \langle 1 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 0\rangle = \langle 1 | \left(\mathbf a^\dag_\lambda - \mathbf a_\lambda\right) | 0\rangle = \left(\langle 1 |\mathbf a^\dag_\lambda \right) | 0\rangle - \langle 1 | \left(\mathbf a_\lambda| 0\rangle\right) = \langle 0 | 0 \rangle - 0 = 1 \\ \end{aligned}
Substituting:
\begin{aligned} \langle \Psi | \mathbf E_{\lambda,z} | \Psi \rangle = & \beta \left(\bar \alpha_1\alpha_2 \times -1 + \bar \alpha_2 \alpha_1 \times 1 \right) \\ = & \beta\left(e^{i\frac{3}{2}\omega_1t}e^{-i\frac{1}{2}\omega_1t} - e^{-i\frac{3}{2}\omega_1t}e^{i\frac{1}{2}\omega_1t} \right) \\ = & \beta\left(e^{i\omega_1t} - e^{-i\omega_1t}\right) = \beta\left(2i \sin(\omega_1t)\right) \\ = &\frac{i}{2}\sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}} \sin\left(\frac{\pi}{L}x\right) \left(2i \sin(\omega_1t)\right) \\ = &-\sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}} \sin\left(\frac{\pi}{L}x\right)\sin\left(\frac{c\pi}{L}t\right) \\ \end{aligned}
For the same box, let’s consider now a multi-mode electric field :
\mathbf E_z = i \sum_m \left(\mathbf a^\dag_m - \mathbf a_m\right) \sqrt{\frac{\hbar\omega_m}{L\varepsilon_0}} \sin(k_m x) = i\sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}}\sum_m \left(\mathbf a^\dag_m - \mathbf a_m\right) \sin\left(\frac{m\pi}{L}x\right)
The state |\Psi_{11s0}\rangle has one photon in mode 1 and an equal linear superposition of 1 photon and zero photon in mode 2.
The energy is:
\begin{aligned} & \varepsilon_{n,\lambda} = \left(n + \frac{1}{2}\right)\hbar\omega_1 \\ & \varepsilon_{1,1} = \left(1 + \frac{1}{2}\right)\hbar\frac{c\pi}{L} = \frac{3\hbar c\pi}{2L} \\ & \varepsilon_{0,2} = \left(0 + \frac{1}{2}\right)\hbar\frac{2c\pi}{L} = \frac{\hbar c\pi}{L} \\ & \varepsilon_{1,2} = \left(1 + \frac{1}{2}\right)\hbar\frac{2c\pi}{L} = \frac{3\hbar c\pi}{L} \end{aligned}
For the mode 1 the state is described by:
| \Psi_1 \rangle = e^{-\left(1+\frac{1}{2}\right)\omega_1t} \mathbf a_1^\dag | 0 \rangle = e^{-\frac{3}{2}\omega_1t} \mathbf a_1^\dag | 0 \rangle
For mode 2 the state is described by:
| \Psi_2 \rangle = \frac{1}{\sqrt2} \left(e^{-\left(1 + \frac{1}{2}\right)\omega_2t} \mathbf a_2^\dag | 0 \rangle + e^{-\left(\frac{1}{2}\right)\omega_2t}| 0 \rangle \right) = \frac{1}{\sqrt2} \left(e^{-\frac{3}{2}\omega_2t} \mathbf a_2^\dag + e^{-\frac{1}{2}\omega_2t} \rangle \right)| 0 \rangle
The multi-mode is:
\begin{aligned} |\Psi_{11s0}\rangle = |\Psi_1 \Psi_2 \rangle = \frac{1}{\sqrt2} \left(e^{-\frac{3}{2}\omega_2t} \mathbf a_2^\dag + e^{-\frac{1}{2}\omega_2t} \right) e^{-\frac{3}{2}\omega_1t} \mathbf a_1^\dag | 0 \rangle \end{aligned}
It is now possible to compute the expectation of the electric field \langle \mathbf E_z \rangle. Rather than do the full computation, using some known results will simplify the mathematics. The computation can be separated for the two separated | \Psi \rangle.
For |\Psi_1 \rangle which corresponds to a single-photon state created by the action of the creation operator \mathbf a_1^\dag on the vacuum state |0\rangle, the expectation value of the electric field in this state is zero.
For |\Psi_2\rangle we can perform a similar computation, without the need to compute the same mode components as will be zero as previously shown just with different variable. Then, there will be only remaining the two component which will be giving the same result (-1 and 1) so the overall component will be oscillating with a frequency \omega_2. Defining some variables:
\begin{aligned} & \alpha_1 = e^{-i\frac{1}{2}\omega_2t} \\ & \alpha_2 = e^{-i\frac{3}{2}\omega_2t} \\ & \beta = \frac{i}{2}\sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}} \sin\left(\frac{2\pi}{L}x\right) \end{aligned}
and using the previous results:
\begin{aligned} \langle \Psi | \mathbf E_{\lambda,z} | \Psi \rangle = & \beta \left(\bar \alpha_1\alpha_2 \times -1 + \bar \alpha_2 \alpha_1 \times 1 \right) \\ = & \beta\left(e^{i\frac{3}{2}\omega_2t}e^{-i\frac{1}{2}\omega_1t} - e^{-i\frac{3}{2}\omega_2t}e^{i\frac{1}{2}\omega_2t} \right) \\ = & \beta\left(e^{i\omega_2t} - e^{-i\omega_2t}\right) = \beta\left(2i \sin(\omega_2t)\right) \\ = &\frac{i}{2}\sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}} \sin\left(\frac{2\pi}{L}x\right) \left(2i \sin(\omega_2t)\right) \\ = &-\sqrt{\frac{\hbar\pi c}{L^2\varepsilon_0}} \sin\left(\frac{2\pi}{L}x\right)\sin\left(\frac{2c\pi}{L}t\right) \\ \end{aligned}