Marco Azimonti Personal Homepage

Quantum Harmonic Oscillator

Before exploring the complexities of the quantum harmonic oscillator, it is instructive to revisit the classical harmonic oscillator. In both classical and quantum mechanics, the harmonic oscillator serves as a fundamental model for understanding vibrational systems. It offers a straightforward first approximation for analyzing more complex scenarios, where systems of many masses connected by springs can often be simplified to a set of individual harmonic oscillators. This simplification allows for a deeper insight into the behavior of physical systems, setting the stage for exploring their quantum counterparts.

Classical harmonic oscillator

The classical harmonic oscillator is an important model in physics, representing a system where a force acts on a mass in such a way as to pull it back towards a central position when it is displaced. This model is pivotal for understanding various physical systems, from molecular vibrations to the principles of quantum mechanics.

System description

Consider a mass m suspended on a spring, oriented vertically along the x-direction (the x-axis is vertical in this case). The mass is subject to a restoring force F that is directly proportional to the displacement x from the equilibrium position, but in the opposite direction. This relationship can be described by Hooke’s law:

F = -k_0x

where k_0 is the spring constant.

The spring is created using a projection of a 3D helix. The parametric equations of an horizontal helix can be written as: x=r\cos(t)\quad y=r\sin(t) \quad z=atThen rotating by an horizontal angle \theta and dropping the z coordinate, a cycloid is created in 2D:x'=r\cos(t)\cos(\theta)-at\sin(\theta), \quad y'=r\sin(t)

Equations of motion

The motion of the mass is governed by Newton’s second law, which states that the force F acting on an object is equal to the mass m of the object multiplied by its acceleration a:

F = ma

Given that acceleration is the second derivative of position x with respect to time t, we can write:

ma = m\frac{\mathrm d^2x}{\mathrm dt^2}

Substituting the expression for F from Hooke’s law:

m\frac{\mathrm d^2x}{\mathrm dt^2} = -k_0x

This leads to the differential equation:

\frac{\mathrm d^2x}{\mathrm dt^2} + \frac{k_0}{m}x = 0

The solution to this differential equation describes simple harmonic motion, with the position x as a function of time t given by:

x(t) = A\cos(\omega t + \phi)

where:

A is the amplitude of the oscillation,
\omega = \sqrt{\frac{k_0}{m}} is the angular frequency of the oscillation,
\phi is the phase constant, determined by the initial conditions of the system.

The classical harmonic oscillator model provides a crucial bridge to understanding more complex and quantum systems, illustrating fundamental concepts of periodic motion and energy conservation.

Quantum mechanic harmonic oscillator

In the quantum mechanic case, the oscillator will be analyzed using the Lagrangian formulation, and work with potential instead. A similar approach is valid also in the classical case, and using the potential:

V(x) = -\int_0^x F(x')\mathrm dx' = \int_0^x k_0x\, \mathrm dx' = \frac{1}{2}k_0x^2 = \frac{1}{2}m\,\omega^2x^2

and the Euler-Lagrange equations would lead to the same motion above.

This potential can be inserted in the Schrödinger equation:

-\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} + \frac{1}{2}m\,\omega^2 x^2\psi(x) = E\psi(x)

It is possible to rewrite this equation in dimensionless unit, defining:

\xi \equiv \sqrt{\frac{m\,\omega}{\hbar}}x

which gives:

\begin{aligned} & -\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} + \frac{1}{2}m\,\omega^2 x^2\psi(x) = E\psi(x) \\ & -\frac{\hbar^2}{2m} \frac{m\,\omega}{\hbar} \frac{\mathrm d^2\psi(\xi)}{\mathrm d \xi^2} + \frac{1}{2}m \frac{\hbar}{m\,\omega}\omega^2 \xi^2\psi(\xi) = E\psi(\xi) \\ & \frac{1}{2} \frac{\mathrm d^2\psi(\xi)}{\mathrm d \xi^2} - \frac{1}{2} \xi^2 \psi(\xi) = -\frac{E}{\hbar\,\omega}\psi(\xi) \\ \end{aligned}

The solution for this problem (without the mathematical derivation at this stage of this solution) is that the wave function is proportional to a Gaussian solution:

\psi(\xi) \propto e^{-\frac{\xi^2}{2}}

with an energy level:

E = \frac{\hbar\,\omega}{2} To find all the solutions, it is then possible to consider a generic solution of the form of:

\psi_n(\xi) = A_n e^{-\frac{\xi^2}{2}}H_n(\xi)

where H_n(\xi) are functions that need to be determined. Substituting into the Schrödinger equation:

\begin{aligned} & \frac{1}{2} \frac{\mathrm d^2}{\mathrm d \xi^2} \left( A_n e^{-\frac{\xi^2}{2}}H_n(\xi) \right) - \frac{1}{2} \xi^2 \left( A_n e^{-\frac{\xi^2}{2}}H_n(\xi) \right) + \frac{E}{\hbar\,\omega}\left( A_n e^{-\frac{\xi^2}{2}}H_n(\xi) \right) = 0 \\ & 2A_n \, e^{-\frac{\xi^2}{2}} \left[ \left( \frac{\mathrm d^2H_n(\xi)}{\mathrm d^2 \xi} - 2\xi \frac{\mathrm dH_n(\xi)}{\mathrm d \xi} + \xi^2 H_n(\xi) \right) - \xi^2 H_n(\xi) + \left(\frac{2E}{\hbar\,\omega} - 1\right) H_n \right] = 0 \\ & 2A_n \, e^{-\frac{\xi^2}{2}} \left[ \frac{\mathrm d^2H_n(\xi)}{\mathrm d^2 \xi} - 2\xi \frac{\mathrm dH_n(\xi)}{\mathrm d \xi} + \left(\frac{2E}{\hbar\,\omega} - 1\right) H_n \right] = 0 \\ & \frac{\mathrm d^2H_n(\xi)}{\mathrm d^2 \xi} - 2\xi \frac{\mathrm dH_n(\xi)}{\mathrm d \xi} + \left(\frac{2E}{\hbar\,\omega} - 1\right) H_n = 0 \end{aligned}

as:

\begin{aligned} \frac{\mathrm d}{\mathrm d \xi} \left(e^{-\frac{\xi^2}{2}}H_n(\xi) \right) & = -\xi e^{-\frac{\xi^2}{2}}H_n(\xi) + e^{-\frac{\xi^2}{2}}\frac{\mathrm dH_n(\xi)}{\mathrm d \xi} \\ \frac{\mathrm d^2}{\mathrm d \xi^2} \left(e^{-\frac{\xi^2}{2}}H_n(\xi) \right) & = \frac{\mathrm d}{\mathrm d \xi} \left[\frac{\mathrm d}{\mathrm d \xi} \left(e^{-\frac{\xi^2}{2}}H_n(\xi) \right) \right] = \frac{\mathrm d}{\mathrm d \xi} \left(-\xi e^{-\frac{\xi^2}{2}}H_n(\xi) + e^{-\frac{\xi^2}{2}}\frac{\mathrm dH_n(\xi)}{\mathrm d \xi}\right) \\ & = \xi^2e^{-\frac{\xi^2}{2}}H_n(\xi) - \xi e^{-\frac{\xi^2}{2}}\frac{\mathrm dH_n(\xi)}{\mathrm d \xi} - \xi^2 e^{-\frac{\xi^2}{2}}\frac{\mathrm dH_n(\xi)}{\mathrm d \xi} + e^{-\frac{\xi^2}{2}}\frac{\mathrm d^2H_n(\xi)}{\mathrm d^2 \xi} \\ & = e^{-\frac{\xi^2}{2}}\left( \frac{\mathrm d^2H_n(\xi)}{\mathrm d^2 \xi} - 2\xi \frac{\mathrm dH_n(\xi)}{\mathrm d \xi} + \xi^2 H_n(\xi) \right) \end{aligned}

The equation:

\frac{\mathrm d^2H_n(\xi)}{\mathrm d^2 \xi} - 2\xi \frac{\mathrm dH_n(\xi)}{\mathrm d \xi} + \left(\frac{2E}{\hbar\,\omega} - 1\right) H_n = 0

is then defining differential equations for the Hermite polynomials. These kind of polynomials are well studied, and a solution exists only if:

\left(\frac{2E}{\hbar\,\omega} - 1\right) = 2n, \quad n \in \mathbb N

Therefore, solutions exist for only specific values of the energy:

E_n = \left(n + \frac{1}{2}\right)\hbar\,\omega, \quad n \in \mathbb N

These levels are equally spaced by a factor \hbar\, \omega and like in the well case, there is a zero-level energy E_0 = \frac{1}{2}\hbar\,\omega, consequence of the quantum confinement.

The first few are:

\begin{aligned} H_0(\xi) &= 1 \\ H_1(\xi) &= 2\xi \\ H_2(\xi) &= 4\xi^2 - 2 \\ H_3(\xi) &= 8\xi^3 - 12\xi \\ H_4(\xi) &= 16\xi^4 - 48\xi^2 + 12 \end{aligned} These are even odd or even (so they have a definite parity).

And there is a recurrence formula for the (n+1)^{th} Hermite polynomial if the n^{th} and the (n-1)^{th} are known:

H_{n+1}(\xi) = 2\xi H_n(\xi) - 2n H_{n-1}(\xi)

The solution can be normalized (and the algebra would involved integral with power and Gaussian which can be calculated) and gives:

A_n = \sqrt{\frac{1}{\sqrt \pi 2^n n!}}

Putting all together:

\begin{aligned} & \psi_n(\xi) = \sqrt{\frac{1}{\sqrt \pi 2^n n!}} e^{-\frac{\xi^2}{2}}H_n(\xi) \\ & E_n = \left(n + \frac{1}{2}\right)\hbar\,\omega, \quad n \in \mathbb N \end{aligned}

In the original coordinated, since \xi = \sqrt{\frac{m\,\omega}{\hbar}}x the solutions are:

\begin{aligned} & \psi_n(x) = \sqrt{\frac{1}{2^n n!}\sqrt{\frac{m\,\omega}{\pi\hbar}}} e^{-\frac{m\,\omega}{2\hbar}x^2}H_n\left(\sqrt{\frac{m\,\omega}{\hbar}}x\right) \\ & E_n = \left(n + \frac{1}{2}\right)\hbar\,\omega, \quad n \in \mathbb N \end{aligned}

It is possible to plot these solutions as function of \xi.

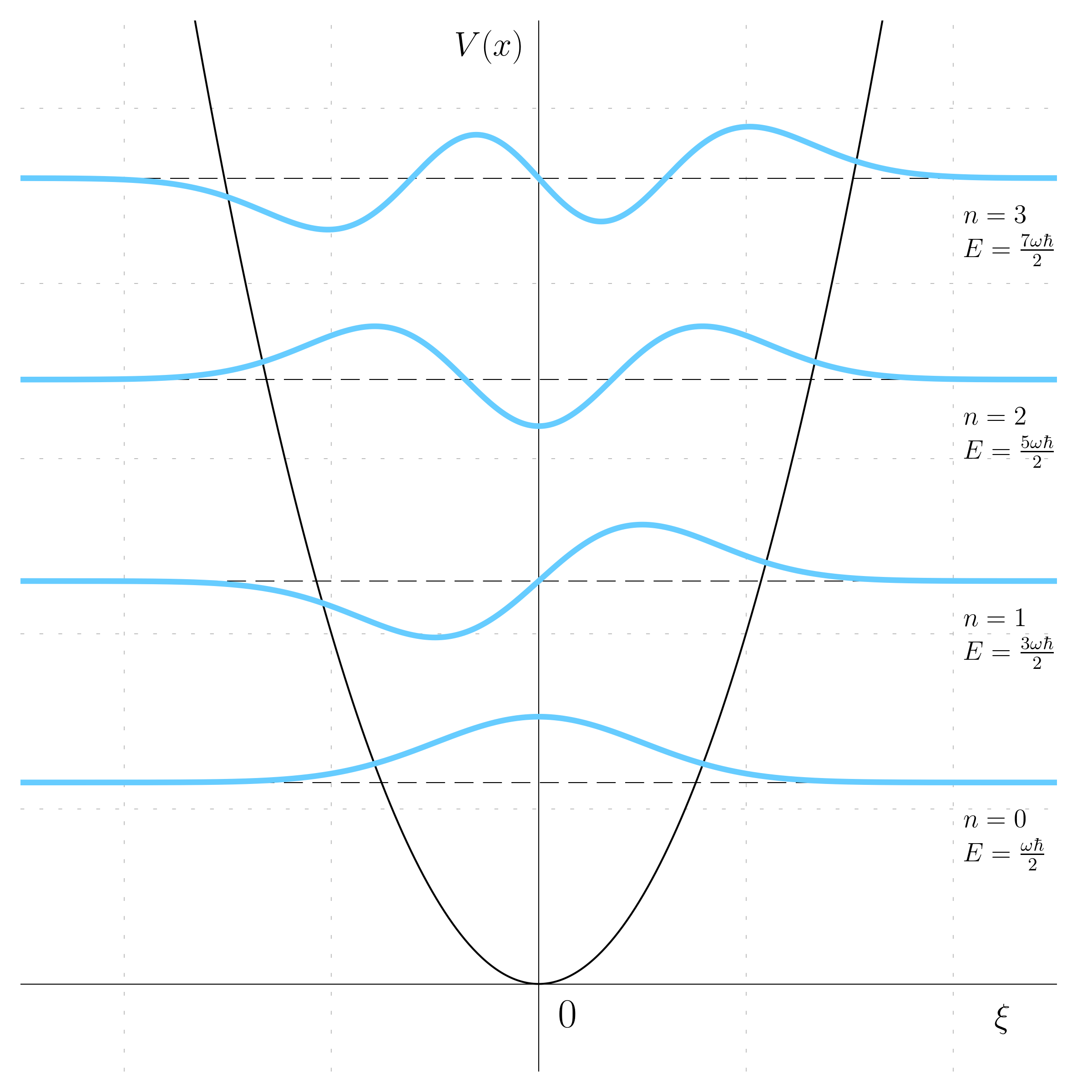
These solutions are plotted as function of the energy levels:

the first solution is just a Gaussian, and it is possible to recognize its characteristic shape, and it is an even function;
the second solution is a Gaussian multiplied by a linear function, and therefore it is an odd function and so on for higher order;
Intersections of the parabola (potential energy) with dashed lines (eigenenergies) represent classical turning points. In a classical oscillator scenario, giving a ball the same amount of energy would result in it moving down, reaching these points, and then reversing direction. These classical turning points are where a classical mass with chosen energy turns around to move back downhill.

There is only one point in those solutions which is different from the classical oscillator, it is that there are no oscillations at all: these are static solutions, taking the modulus square of these and the probability distribution is not changing.

To resolve this apparent contradiction, it is necessary to look at the time-dependent Schrödinger equation.

Raising and lowering operators for the harmonic oscillator

Starting from the dimensionless Schrödinger equation:

\frac{1}{2} \left(-\frac{\mathrm d^2}{\mathrm d \xi^2} + \frac{1}{2} \xi^2\right) \psi(\xi) = \frac{E}{\hbar\,\omega}\psi(\xi)

It is possible to write the left hand side as sort of sum of difference of squares:

\frac{1}{\sqrt 2} \left(-\frac{\mathrm d}{\mathrm d \xi} + \xi\right)\frac{1}{\sqrt 2} \left(\frac{\mathrm d}{\mathrm d \xi} + \xi\right) = \frac{1}{2} \left(-\frac{\mathrm d^2}{\mathrm d \xi^2} + \frac{1}{2} \xi^2\right) - \frac{1}{2} \left(\frac{\mathrm d}{\mathrm d \xi}\xi - \xi \frac{\mathrm d}{\mathrm d \xi} \right)

acting the second term on an arbitrary function f(\xi):

\left(\frac{\mathrm d}{\mathrm d \xi}\xi - \xi \frac{\mathrm d}{\mathrm d \xi} \right)f(\xi) = \frac{\mathrm d (f(\xi)\xi)}{\mathrm d \xi} - \xi \frac{\mathrm df(\xi)}{\mathrm d \xi} = \frac{\mathrm d f(\xi)}{\mathrm d \xi}\xi + \frac{\mathrm d \xi}{\mathrm d \xi}f(\xi) - \xi \frac{\mathrm df(\xi)}{\mathrm d \xi} = f(\xi)

so the term is equal to 1 and the equation simplifies to:

So, with the definition of the lowering or annihilation operator \mathbf a as:

\mathbf a \equiv \frac{1}{\sqrt 2} \left(\frac{\mathrm d}{\mathrm d \xi} + \xi\right)

and the raising or creation operator as:

\mathbf a^\dag \equiv \frac{1}{\sqrt 2} \left(-\frac{\mathrm d}{\mathrm d \xi} + \xi\right)

These are Hermitian adjoints:

\begin{aligned} & \left(\overline{\frac{\mathrm d}{\mathrm d \xi}} \right) = -\left(\frac{\mathrm d}{\mathrm d \xi} \right) \\ & \bar \xi = \xi \\ & (\mathbf {\bar a})^T = \frac{1}{\sqrt 2} \left(-\frac{\mathrm d}{\mathrm d \xi} + \xi\right) = \mathbf a^\dag \end{aligned}

The first result come from the fact that the derivative operator is antisymmetric (in the derivation of the Schrödinger equation is multiplied by i\hbar in order to make it Hermitian) and the second from the fact that the position operator is Hermitian, so that prove that these are indeed the adjoints of each other; these operators are not Hermitian, as they are (follow the definition not the same as it would be required for Hermiticity).

The Schrödinger equation becomes:

\left(\mathbf a^\dag \mathbf a + \frac{1}{2}\right) \psi(\xi) = \frac{E}{\hbar\,\omega}\psi(\xi)

The Hamiltonian can be written as:

\mathbf H = \hbar \omega \left(\mathbf a^\dag \mathbf a + \frac{1}{2}\right)

Since the energy was computed as:

E_n = \left(n + \frac{1}{2}\right)\hbar\,\omega, \quad n \in \mathbb N

Then:

\mathbf a^\dag \mathbf a | \psi_n \rangle = \mathbf N | \psi_n \rangle = n | \psi_n \rangle

So the number operator \mathbf N:

\mathbf N \equiv \mathbf a^\dag \mathbf a

has the harmonic oscillator eigenstates n as its eigenvalues.

The commutator of these operator is:

\begin{aligned} \left[\mathbf a \mathbf a^\dag\right] & = \mathbf a\mathbf a^\dag - \mathbf a^\dag \mathbf a =\frac{1}{\sqrt 2} \left(\frac{\mathrm d}{\mathrm d \xi} + \xi\right)\frac{1}{\sqrt 2} \left(-\frac{\mathrm d}{\mathrm d \xi} + \xi\right) - \frac{1}{\sqrt 2} \left(-\frac{\mathrm d}{\mathrm d \xi} + \xi\right)\frac{1}{\sqrt 2} \left(\frac{\mathrm d}{\mathrm d \xi} + \xi\right) \\ & = \frac{1}{2}\left[-\frac{\mathrm d^2}{\mathrm d \xi^2} +\xi^2 + \left(\frac{\mathrm d}{\mathrm d \xi}\xi - \xi \frac{\mathrm d}{\mathrm d \xi} \right) \right] - \frac{1}{2}\left[-\frac{\mathrm d^2}{\mathrm d \xi^2} + \xi^2 + \left(-\frac{\mathrm d}{\mathrm d \xi}\xi + \xi \frac{\mathrm d}{\mathrm d \xi} \right) \right] \\ & = \frac{1}{2}\left[-\frac{\mathrm d^2}{\mathrm d \xi^2} +\xi^2 + \left(\frac{\mathrm d}{\mathrm d \xi}\xi - \xi \frac{\mathrm d}{\mathrm d \xi} \right) \right] - \frac{1}{2}\left[-\frac{\mathrm d^2}{\mathrm d \xi^2} + \xi^2 + \left(-\frac{\mathrm d}{\mathrm d \xi}\xi + \xi \frac{\mathrm d}{\mathrm d \xi} \right) \right] \\ & = -\frac{1}{2}\frac{\mathrm d^2}{\mathrm d \xi^2} + \frac{1}{2}\xi^2 + \frac{1}{2}\left(\frac{\mathrm d}{\mathrm d \xi}\xi - \xi \frac{\mathrm d}{\mathrm d \xi} \right) + \frac{1}{2}\frac{\mathrm d^2}{\mathrm d \xi^2} - \frac{1}{2}\xi^2 + \frac{1}{2} \left(\frac{\mathrm d}{\mathrm d \xi}\xi + \xi \frac{\mathrm d}{\mathrm d \xi} \right) \\ & = \left(\frac{\mathrm d}{\mathrm d \xi}\xi + \xi \frac{\mathrm d}{\mathrm d \xi} \right) = 1 \end{aligned}

This property:

\left[\mathbf a \mathbf a^\dag\right] = \mathbf a\mathbf a^\dag - \mathbf a^\dag \mathbf a = 1

can be used to show the reason of the names of these operators:

\begin{aligned} & \mathbf a \left(\mathbf a^\dag \mathbf a \right) | \psi_n \rangle = \mathbf a n | \psi_n \rangle \\ & \left(\mathbf a \mathbf a^\dag \right) \mathbf a | \psi_n \rangle = n | \mathbf a \psi_n \rangle \\ & \left(\mathbf a^\dag \mathbf a + 1 \right) \mathbf a | \psi_n \rangle = n \mathbf a | \psi_n \rangle \\ & \mathbf a^\dag \mathbf a \left(\mathbf a | \psi_n \rangle\right) = (n-1) \left(\mathbf a | \psi_n \rangle\right) \end{aligned}

But the right hand side is simply |\psi_{n-1}\rangle so:

\mathbf a | \psi_n \rangle = A_n | \psi_{n-1} \rangle

so the lowering operator change the state | \psi_n \rangle to | \psi_{n-1} \rangle.

We can perform the same with \mathbf a^\dag:

\begin{aligned} & \mathbf a^\dag \left(\mathbf a^\dag \mathbf a \right) | \psi_n \rangle = \mathbf a^\dag n | \psi_n \rangle \\ & \mathbf a^\dag \left(\mathbf a \mathbf a^\dag - 1 \right) | \psi_n \rangle = \mathbf a^\dag n | \psi_n \rangle \\ & \left(\mathbf a^\dag \mathbf a \right) \mathbf a^\dag | \psi_n \rangle = (n+1) \mathbf a^\dag | \psi_n \rangle \\ & \mathbf a^\dag \mathbf a \left(\mathbf a^\dag | \psi_n \rangle\right) = (n+1) \left(\mathbf a^\dag | \psi_n \rangle\right) \end{aligned}

But the right hand side is simply |\psi_{n+1}\rangle so:

\mathbf a^\dag | \psi_n \rangle = B_{n+1} | \psi_{n+1} \rangle

so the raising operator change the state | \psi_n \rangle to | \psi_{n+1} \rangle.

The coefficients can be computed:

\begin{aligned} & \langle \psi_{n-1} | \mathbf a | \psi_n \rangle = \langle \psi_{n-1} | A_n | \psi_n \rangle = A_n \\ & \langle \psi_{n-1} | \mathbf a | = \left( \mathbf a^\dag | \psi_{n-1} \rangle \right)^\dag = \left( B_n | \psi_n \rangle \right)^\dag = \bar B \langle \psi_n | \\ & \langle \psi_{n-1} | A_n | \psi_{n} \rangle = \bar B \langle \psi_n | \psi_n \rangle = \bar B_n \\ & \mathbf a^\dag \mathbf a | \psi_n \rangle = A_n \mathbf a^\dag |\psi_{n-1} \rangle = A_n B_n |\psi_{n} \rangle = \left|A_n B_n\right|^2 |\psi_{n} \rangle = n |\psi_{n} \rangle \end{aligned}

Which gives (with a multiplication of a complex constant)

A_n = B_n = \sqrt n

And therefore the eigenequation can be rewritten as:

\begin{aligned} & \mathbf a | \psi_n \rangle = \sqrt n | \psi_{n-1} \rangle \\ & \mathbf a^\dag | \psi_n \rangle = \sqrt {n+1} | \psi_{n+1} \rangle \end{aligned}

Returning to the harmonic oscillator, since the lowest state is n=0:

\mathbf a | \psi_0 \rangle = \frac{1}{\sqrt 2} \left(\frac{\mathrm d}{\mathrm d \xi} + \xi\right) \psi_0 (\xi) = 0

For which the solution is:

\psi_0(\xi) = \frac{1}{\sqrt[4]\pi} e^{-\frac{\xi^2}{2}}

Applying the raising operators multiples times:

\begin{aligned} & \left(\mathbf a^\dag \right)^n = \sqrt{n!} |\psi_n \rangle \\ & |\psi_n \rangle = \frac{1}{\sqrt{n!}} \left(\mathbf a^\dag \right)^n \end{aligned}

which can be used to progressively construct the solutions for increasing value of n.