Uncertainty Principle And Bell's Theorem
Introduction
In the intricate landscape of quantum mechanics, the Heisenberg Uncertainty Principle and Bell’s Theorem stand as pivotal concepts that challenge our classical intuitions about the universe. While traditional approaches often explore these principles through dense historical contexts and complex examples, such as Heisenberg’s original discussions on position and momentum measurements or extensive explanations involving Fourier transforms, a refreshingly clear perspective was offered by Professor Richard Feynman. Drawing from an elegant analogy introduced by Professor David Mermin, Feynman’s explanation demystifies these quantum phenomena in a straightforward yet profound manner.
Inspired by this approach, this article aims to distill these complex theories into their essence using the same initial simplicity. From there, I will expand into a rigorous, mathematically rich exploration of their implications and proofs, weaving through the quantum mechanical framework to provide a comprehensive understanding of these fundamental principles.
Apparatus Description
The experimental setup for illustrating the principles of quantum mechanics involves a simple yet ingenious apparatus. Central to this experiment are three unassuming boxes, each sealed to ensure their contents remain unseen and undisturbed. These boxes are designated as L, C, and R, corresponding to the left, center, and right positions, respectively. Attached to each box is a button, and pressing one of these buttons activates a mechanism within the box.
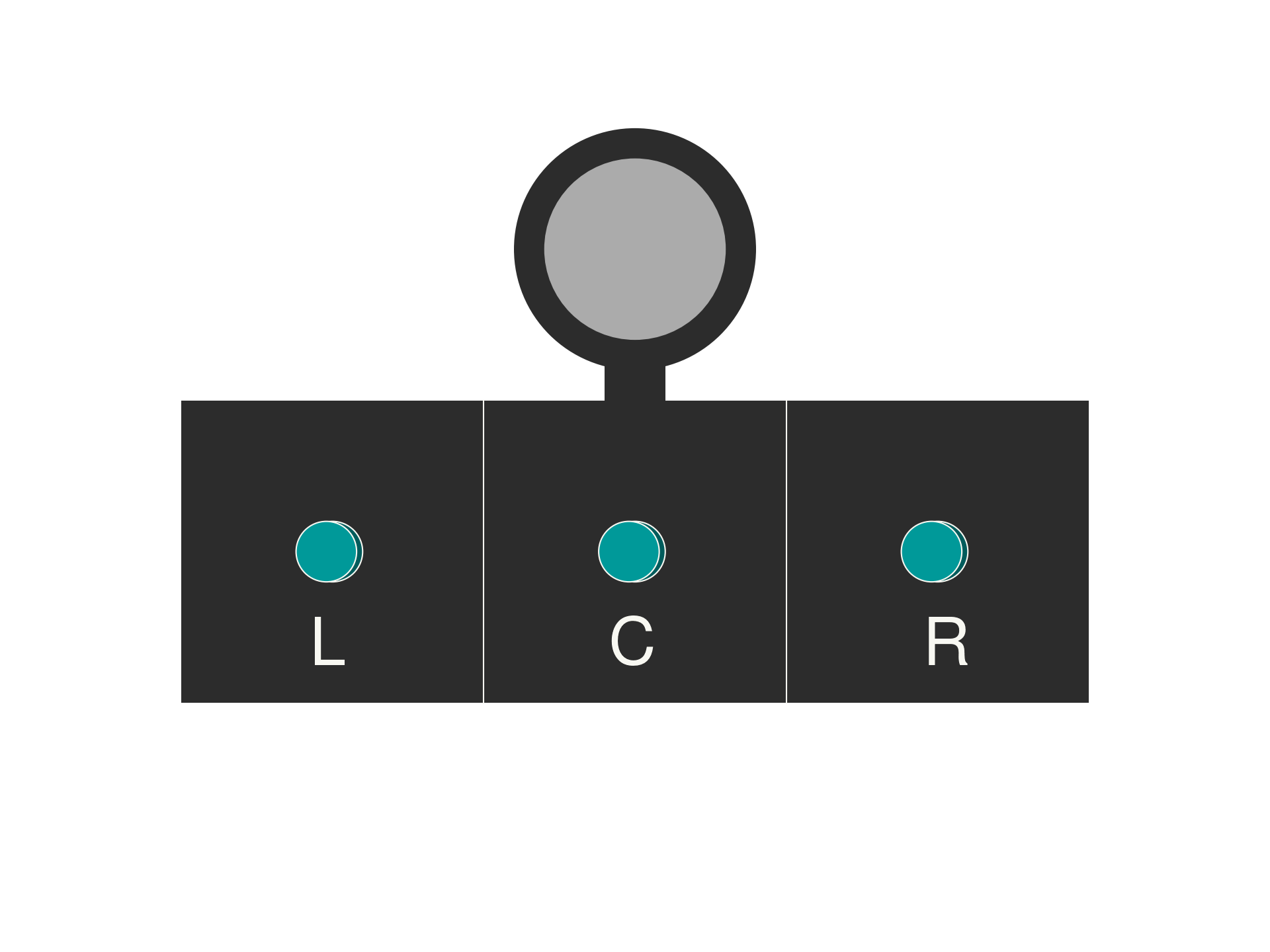
Each box contains a bulb which, upon pressing the associated button, lights up in one of two colors: red or blue. The outcome is entirely random, mimicking the probabilistic nature of quantum phenomena. Participants in the experiment are tasked with pressing any of the three buttons and recording the resulting color of the bulb. This seemingly simple action, repeated under controlled conditions, sets the stage for a deeper exploration of quantum mechanics.
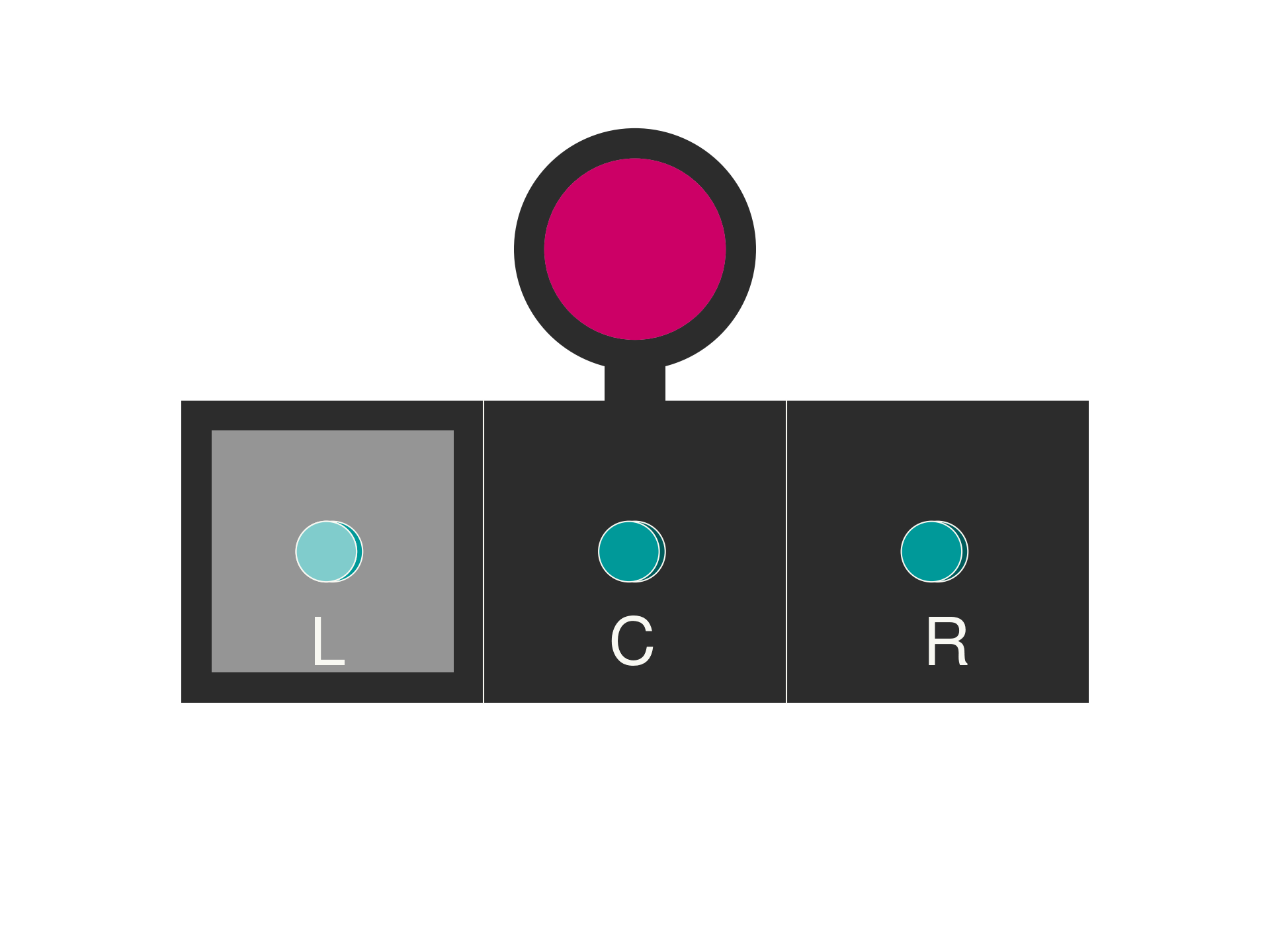
As the narrative of the experiment expands, a second, identical apparatus is introduced. This addition allows for the exploration of more complex scenarios, including entanglement and non-locality, as envisioned by Bell’s Theorem. The introduction of a second apparatus not only enriches the experiment but also underscores the intricate linkages and correlations that define the quantum world. This setup, while elementary in its construction, provides profound insights into the fundamental uncertainties and the interconnected reality that quantum theory proposes.
Classical View
In a classical interpretation of our experiment involving the three-box apparatus, we might begin by assuming that the internal mechanism of each box has predetermined states. Let’s consider a scenario where the system could be in one of eight possible states, each equally likely to occur. These states are defined as RRR, RBR, RBB, RRB, BRR, BRB, BBR and BBB, with R representing a red light and B a blue light, the order is for the Left (L), Center (C) and Right (R) box. Each state has a probability of ⅛ of being the actual configuration at any given time.
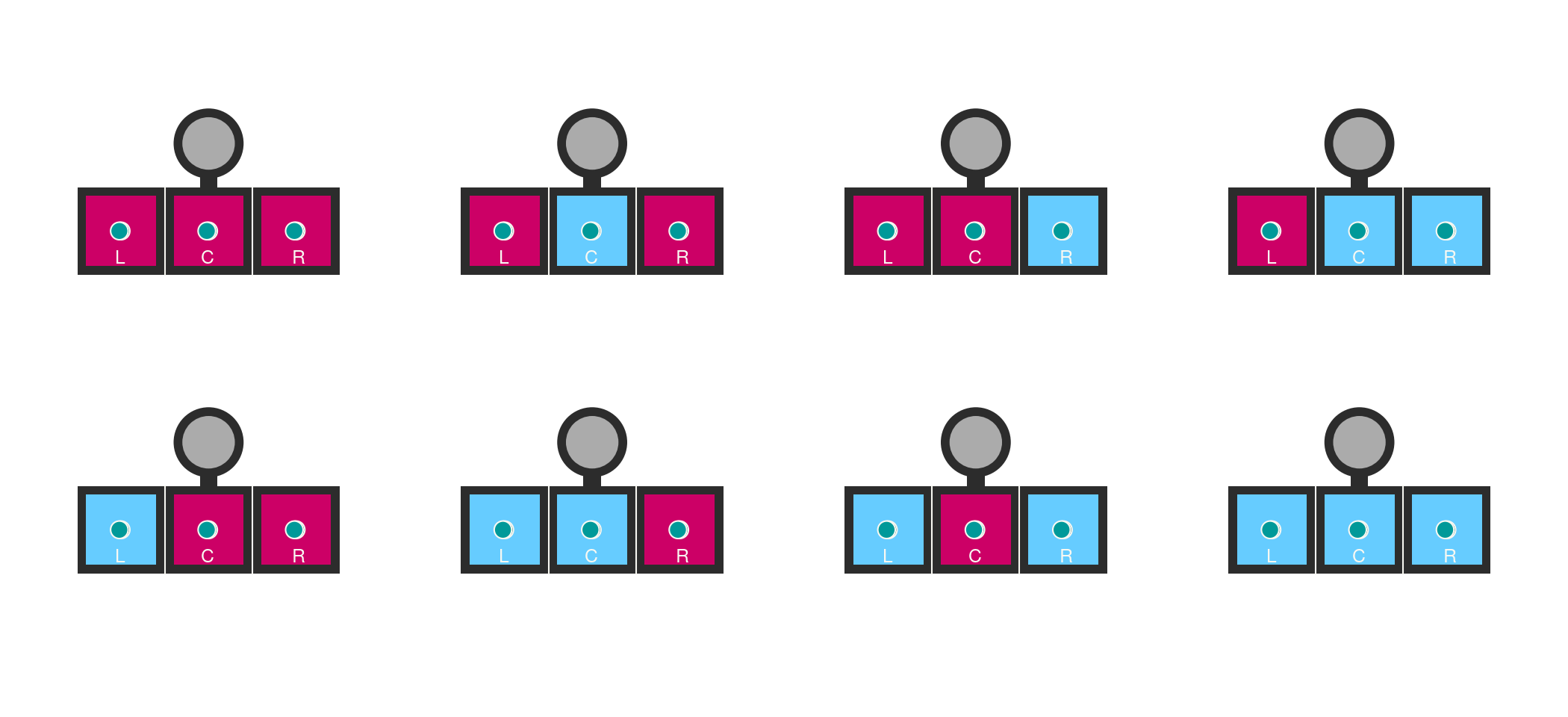
Given this setup, we can analyze the probabilities related to the outcomes when pressing the buttons corresponding to each box. A key question we might ask is: if we press two random buttons, what is the minimum probability that the second time the box will yield a light of the same color?
We need to evaluate the agreement between pairs (LC, LR, CR) for each configuration:
| State | LC |
LR |
CR |
Prob |
|---|---|---|---|---|
RRR |
✓ | ✓ | ✓ | 1 |
RBR |
✗ | ✓ | ✗ | ⅓ |
RBB |
✗ | ✗ | ✓ | ⅓ |
RRB |
✓ | ✗ | ✗ | ⅓ |
BRR |
✗ | ✗ | ✓ | ⅓ |
BRB |
✗ | ✓ | ✗ | ⅓ |
BBR |
✓ | ✗ | ✗ | ⅓ |
BBB |
✓ | ✓ | ✓ | 1 |
From the table when selecting any two of the three box the probability that they match is at least ⅓ (except the degenerated two cases when they all match).
The hidden variables hypothesis aligns with this classical perspective, suggesting that the observable outcomes in our three-box experiment are predetermined by internal states encoded at the time of creation. This notion parallels the concept of “elements of reality” discussed in the EPR paper (more below), where these hidden variables dictate the light color (R or B) without influence from subsequent measurements.
In our setup, each hidden variable specifies the color state for a specific box (L, C, R). Thus, regardless of the observer’s actions, the outcomes are fixed independently if a measurement is made or not. The table demonstrates that for any pair of boxes (LC, LR, CR), the probability of observing two lights of the same color in a single trial is at least ⅓. This is the minimal expected match rate across all possible states, with some scenarios guaranteeing matches in all comparisons.
The consistent with the ⅓ minimum match probability underscores the concept of Bell’s Inequality. It states that in a local hidden variable theory, certain statistical predictions (such as correlations between distant events) must satisfy specific inequalities. Our analysis, by showing a consistent minimum match rate, reflects such classical predictions and sets a benchmark for comparing against quantum mechanical results, where entanglement might allow for correlations that violate these classical bounds and therefore refute the classical (and the hidden variable) model.
Quantum Mechanical View
Uncertainty principle
Transitioning to a quantum mechanics perspective, the behavior of the apparatus introduces intriguing nuances that deviate from classical expectations. In this quantum version of the apparatus, each button still corresponds to a bulb that lights up in one of two colors: red or blue. However, the outcomes exhibit quantum characteristics, particularly in how the states are determined. There are apparatus that show this behavior but the mathematics is not trivial so will be described later in some details.
A key feature of the quantum apparatus is that pressing any button consistently and continuously results in the same color output for as long as the button is held down. This behavior aligns with the quantum property of state persistence, where the system remains in the same state unless acted upon or observed in a new context.
The quantum mechanical nature of the apparatus is most evident when considering the sequential pressing of different buttons. If you press the left button L and observe a red light R, the system’s state aligns with this observation. However, the subsequent interactions show non-classical behavior:
- Pressing the center button
Cimmediately results in a red lightRonly ¼ of the time, and a blue lightB¾ of the time. - After observing (for example)
Rat the center buttonC, repeating this measurement will consistently yieldRagain. This indicates a state collapse toRatC. - If now one presses the right button
Ror goes back to the left buttonL, the outcomes adhere to the new state probabilities, where the same color as the last observed (R) emerges only ¼ of the time, and the opposite color (B) appears ¾ of the time.
Thus, the act of pressing another button not only resets the informational context of the system but also demonstrates the non-classical, probabilistic nature of quantum mechanics. It highlights how each new measurement can fundamentally shift the state probabilities, overriding previous observations and setting a new quantum context.
In the context of quantum mechanics, this experimental behavior—where pressing one button affects the outcomes of subsequent measurements—serves as a vivid demonstration of the Heisenberg uncertainty principle. In the analogy of the apparatus with three buttons, if we measure the color at the left button L (say it’s consistently red R), and then press the center button C, this action can alter the outcome of L when it is measured again.
This characteristic is directly aligned with the principle articulated by Heisenberg. He posited that certain pairs of physical properties, like position and momentum, cannot both be precisely measured or known simultaneously. In our apparatus analogy, pressing the button L to measure color establishes a certain state, but as soon as C is pressed, the state of L becomes uncertain. If C is then measured and found to be blue B, returning to measure L may not yield red R as initially observed; the outcome could now be blue B instead.
This exemplifies the uncertainty principle because the measurement of one property (C’s color) has disturbed the initial state of another property (L’s color). Just as in quantum mechanics where measuring a particle’s position with high precision can disrupt its momentum, in our simplified model, pressing one button can irreversibly impact the outcome of the previous measurement. This highlights the inherent limitations in obtaining precise information about quantum systems and illustrates the principle that the act of measurement itself can alter the state of the system.
Entanglement and Replication
We have already established that it is not feasible to determine the color of the box simply based on probabilities, nor is it possible to directly observe the internal state to ascertain the contents. Despite these constraints, an intriguing aspect of our quantum system is the ability to replicate the box’s state.
Suppose we devise an alternative method that doesn’t involve the traditional act of pressing buttons or tampering with the mechanism beneath the switches. Let’s imagine a scenario where we discover a method to indirectly infer that a box is set to display red R. Upon using this method, we can press the button to confirm our prediction—consistently finding that the light turns red R. This consistency across tests confirms the accuracy of our replication method.
However, employing this novel approach introduces complexities. If we use this method to predict the color without altering the box’s state, and then check our prediction by pressing the button, the expected outcome should align with our prediction due to the box’s replicated state. Nonetheless, if we were to investigate further, perhaps by trying to use a different method or sequence of button presses to gauge other properties, we might find ourselves in a predicament.
Any attempt to exploreer or alter the experimental approach might influence the outcomes, reflecting the inherent uncertainties and entangled nature of quantum systems. This concept underscores that while replication of the quantum state is possible, any further investigation or alternative measurement strategy could potentially disturb the system, aligning with the fundamental tenets of quantum mechanics.
In traditional classical physics, it was common to discuss the potential states or conditions of a system before an observation or measurement was made. For example one might speculate whether the light is R or B, treating both possibilities as potentially real until verified.
However, in quantum mechanics, this approach encounters fundamental difficulties. Quantum theory requires a departure from the concept of discussing unmeasured potentialities as if they are certain realities. This shift is underscored by the peculiar behavior observed in our quantum box analogy.
When dealing with quantum systems, such as our boxes configured to display certain colors based on button presses, the notion of predetermined potential outcomes—like assuming specific colors are ready to be displayed before a button is pressed—becomes problematic. Quantum mechanics teaches us that the properties of a system are not definitively set until they are observed. Prior to pressing a button, the colors of the boxes are not just unknown; they do not exist in a definite state. This is not merely a limitation of our knowledge, but a fundamental property of how reality operates at the quantum level.
The implication is profound: discussing what might be in a quantum system before we measure it (the “potentialities”) leads to inconsistencies when we attempt to apply classical reasoning. If we say, “The light is either red or blue,” and then attempt to verify this by opening the icebox (pressing the button), we find that our classical expectations do not hold. The act of measurement itself influences the system, often causing what appears to be a change in the state of the system that contradicts the classical idea of fixed potentialities.
Thus, in quantum mechanics, we are compelled to focus solely on measurable outcomes. Theoretical discussions about what might exist or happen prior to measurement are not just unproductive; they are fundamentally at odds with the principles of quantum theory. This marks a radical shift from classical thinking and highlights the unique and often counterintuitive nature of quantum mechanics.
EPR Paradox
The debate over quantum mechanics and its interpretation deepened with the publication of the Einstein-Podolsky-Rosen (EPR) paper in 1935. Einstein, along with his colleagues Boris Podolsky and Nathan Rosen, expressed significant reservations about the prevailing interpretations of quantum mechanics, particularly concerning the Heisenberg Uncertainty Principle.
The EPR argument centers around the concept of quantum entanglement, which they used to challenge the completeness of quantum mechanics. In their thought experiment, they considered a pair of particles that were once connected but later separated by a significant distance. According to quantum theory, measurements performed on one particle can instantaneously affect the state of the other, regardless of the distance separating them. This phenomenon, now called “entanglement,” seemed to Einstein and his co-authors to imply “spooky action at a distance,” as Einstein famously phrased it. Einstein, Podolsky, and Rosen crafted their argument around the idea of perfect correlations between entangled particles. If one could measure the position of one particle, quantum mechanics implies that the position of the other would be known instantly. Similarly, measuring the momentum of one would reveal the momentum of the other. They argued that since both position and momentum could be predicted with certainty without disturbing the other particle, the quantum description of reality must be incomplete. They believed that there must be hidden variables—undetected factors influencing the particles’ behaviors.
The EPR paper posited that if quantum mechanics were correct, then these instantaneous effects would violate the principle of locality, a cornerstone of relativity, which states that an object can only be influenced by its immediate surroundings. The paper essentially challenged the idea that quantum mechanics could be a complete theory on its own, suggesting that additional variables must exist to account for these predictions.
The Einstein-Podolsky-Rosen (EPR) argument translates effectively into the framework of our simplified apparatus analogy. In the EPR scenario, the pair of particles are designed such that the measurement of one directly influences or determines the state of the other, despite any spatial separation. This idea can be likened to having two synchronized boxes in our experimental setup, where pressing a button on one box effectively replicates the effect of pressing a corresponding button on the other box:
-
Mirror Effect of Momentum: In EPR, the momentum of the two particles is correlated such that measuring the momentum of one particle (considered to be moving in one direction) allows for the prediction of the momentum of the other particle (moving in the opposite direction, as if through a mirror). In our apparatus, if pressing the left button
Lon one box results in a red lightR, pressing the corresponding left button on the second box would also result in a red light, effectively mirroring the state despite their separateness. -
Position Equivalence: Similarly, if position corresponds to the specific color state in our boxes (red
Ror blueB), knowing the outcome from one box immediately informs us of the outcome in the other box. If box 1’s center buttonCreveals blueB, then box 2’s center button, when pressed, would reveal the same blueB, mimicking the EPR scenario where knowing the position of one particle informs the position of the other.
The EPR paradox challenges the Heisenberg Uncertainty Principle by setting up a situation where both the position and momentum (or their analogs in our boxes, color and position of switches) seem to be determinable without direct measurement of both at the same instant on the same system. By measuring the “momentum” (outcome of one box) and “position” (outcome of the corresponding button on the other box), the EPR thought experiment argues against the principle that these complementary variables cannot both be precisely measured or known simultaneously due to the quantum uncertainty inherent in such measurements.
In the context of our simple apparatus, this translates to being able to predict the outcomes on one box based on measurements from the other, thus bypassing direct interaction with or measurement of the second box’s state. This illustrative setup helps conceptualize how entanglement and the EPR paradox challenge fundamental quantum mechanics principles, proposing that under certain conditions, the quantum state of a system can be inferred without direct observation, seemingly violating the uncertainty principle.
However, as demonstrated by David Mermin using a realistically entangled quantum system—analogous to our simplified apparatus—it becomes clear that the assumptions of hidden variables posited by the EPR paper do not hold up. This empirical evidence supports the intrinsic randomness and interconnectedness of quantum states, refuting the necessity for hidden variables in explaining quantum phenomena.
Conclusion
In summarizing, while some theoretical frameworks might propose the existence of a superluminal force to account for quantum entanglements, such notions introduce unnecessary complications. These hypothetical forces, though they align outcomes precisely, do not alter the observable results of experiments. Therefore, it is pragmatic to focus on the empirical outcomes rather than speculating about unseen, instantaneous mechanisms. The simplest explanation remains that quantum results are as observed, without invoking hidden variables or unseen forces.
In light of quantum mechanics and experiments like those of Mermin, we must relinquish the classical notion of locality - the idea that objects are only influenced by their immediate surroundings. Quantum entanglement demonstrates that particles can influence each other instantaneously over vast distances, challenging this traditional understanding and highlighting non-local interactions as a fundamental aspect of quantum reality.
Quantum mechanics upholds a nuanced version of locality, asserting that information cannot travel faster than light. Thus, even within highly entangled systems, the measurement on one does not alter the outcome on the other in the conventional sense. The interaction between such systems, described through the density matrix, remains unaffected—adhering to principles where time evolution is governed by unitary operators, although exploring this would require extensive technical exposition. This adherence to a modified form of locality underscores my acceptance of quantum mechanics and entanglement as the most precise models of natural phenomena currently available, despite their counterintuitive aspects.
References
EINSTEIN, Albert, PODOLSKY, Boris, ROSEN, Nathan, 1935. Can quantum-mechanical description of physical reality be considered complete? Physical Review 41, 777 (15 May 1935).
BELL, John S., 1964. On the Einstein Podolsky Rosen paradox. Physics 1, 195 (1964).
MERMIN, David, 1985. Is the Moon There When Nobody Looks? Reality and the Quantum Theory. Physics Today, 38, pp. 38-47.
FEYNMAN, Richard, 1983. Quantum Mechanical View of Reality: Workshop at Esalen [video]. Esalen.