Spherical Harmonics Visualization
In this section, I explore the realm of spherical harmonics visualization, extending our mathematical journey into visual exploration. Building upon the rigorous groundwork laid in the discussion of angular momentum, I now transition to visualizing spherical harmonics. This shift from abstract mathematical formulas to tangible visual representations facilitates a deeper comprehension of these complex functions, pivotal in various domains of physics and engineering. For insights into angular momentum and its mathematical treatment, refer to my previous article here.
Spherical harmonics are a set of functions defined on the surface of a sphere, characterized by two integers: \ell (the degree) and m (the order). These functions form an orthonormal basis for the space of square-integrable functions on the sphere. In this article, we will visualize the spherical harmonics for \ell=1, 2, 3 using the Condon-Shortley phase convention, which defines the real basis of spherical harmonics Y_{\ell,m} in terms of their complex analogues Y_{\ell,m} as:
Y_{\ell,m} = \begin{cases} \sqrt 2 \,(-1)^m \,\Im\left\{Y_{\ell,|m|}\right\} & m < 0 \\ Y_{\ell,0} & m = 0 \\ \sqrt 2 \, (-1)^m \, \Re\left\{Y_{\ell,m}\right\} & m > 0 \end{cases}
This convention is useful because the resulting real spherical harmonics Y_{\ell,m} inherit the important properties of the complex spherical harmonics, such as orthogonality and completeness, while also being more intuitive to visualize and interpret in many applications.
The orthogonality property ensures that the real spherical harmonics are mutually perpendicular to each other with respect to the inner product defined on the sphere. This property is crucial for representing functions as a series expansion in terms of spherical harmonics, as it allows for a unique decomposition of the function into its spherical harmonic components.
Moreover, the real spherical harmonics are normalized, meaning their norm (or length) is unity when integrated over the sphere. This normalization property ensures that the coefficients in the series expansion have a well-defined meaning and can be interpreted as the “amount” of each spherical harmonic present in the function.
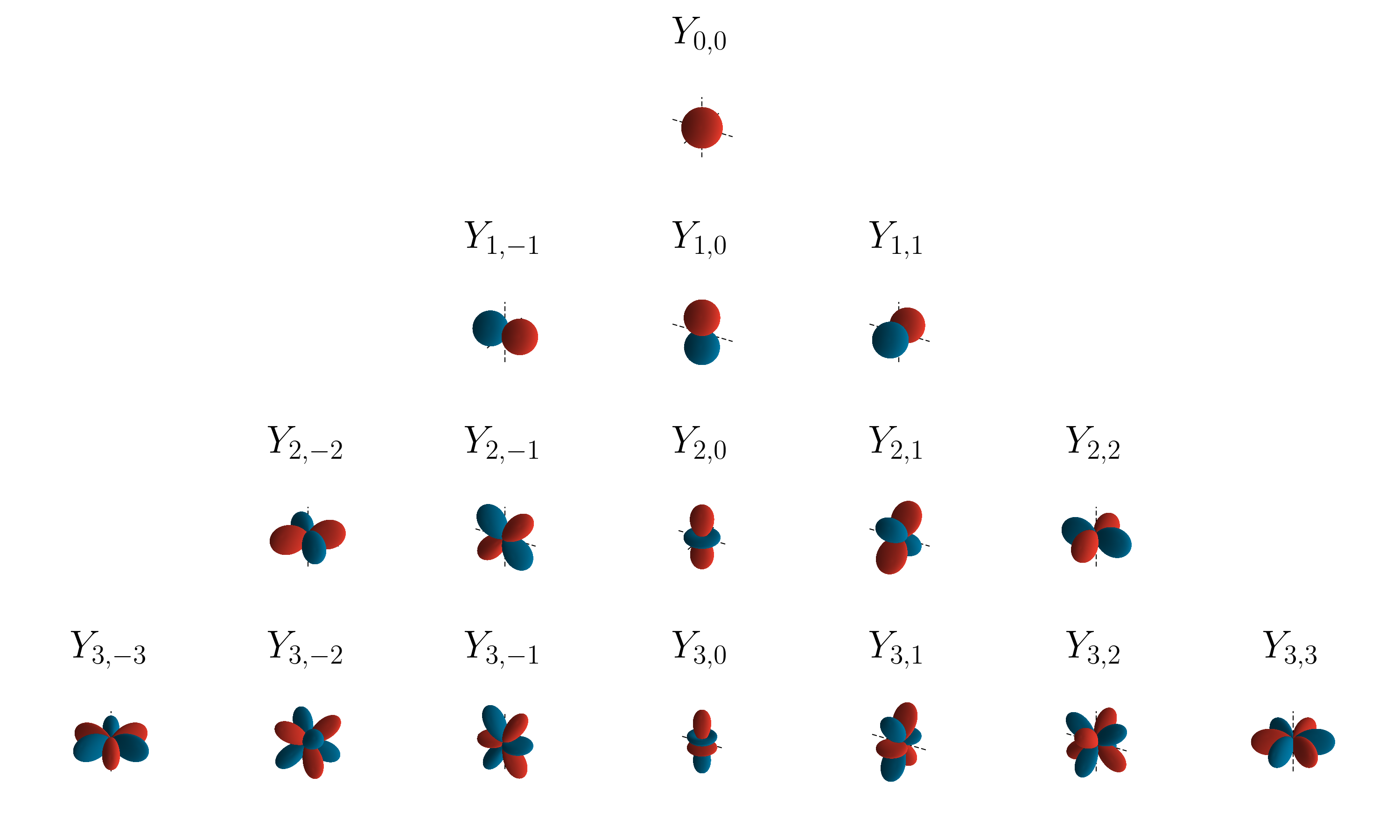
Visual representations of the first few real spherical harmonics. Orange portions represent regions where the function is positive, and blue portions represent where it is negative. The distance of the surface from the origin indicates the absolute value of Y_{\ell,m}(\theta ,\phi ) in angular direction (\theta ,\phi).
By defining the real spherical harmonics using the Condon-Shortley phase convention, we obtain a set of real-valued functions that form an orthonormal basis set for the space of square-integrable functions on the sphere. This basis set is particularly useful in various fields, such as quantum mechanics, electromagnetics, and computer graphics, where the analysis and visualization of functions defined on spherical surfaces play a crucial role.
It is possible to analyze a few of the spherical harmonics; to make the intuition they will be compared to the vibration of the shell, which solution has the spherical harmonics as the amplitude (real) of the vibration.
For \ell=0 there is a single function for m=0, which has the form:

This is called the “breathing” mode of the shell, which move equally in all direction, and since the spherical harmonic is the amplitude, it is just a constant, so it is a fix sphere of unit amplitude; this is the only mode in which there are no zeros to the function.
\ell=1 and m=0 has the form:
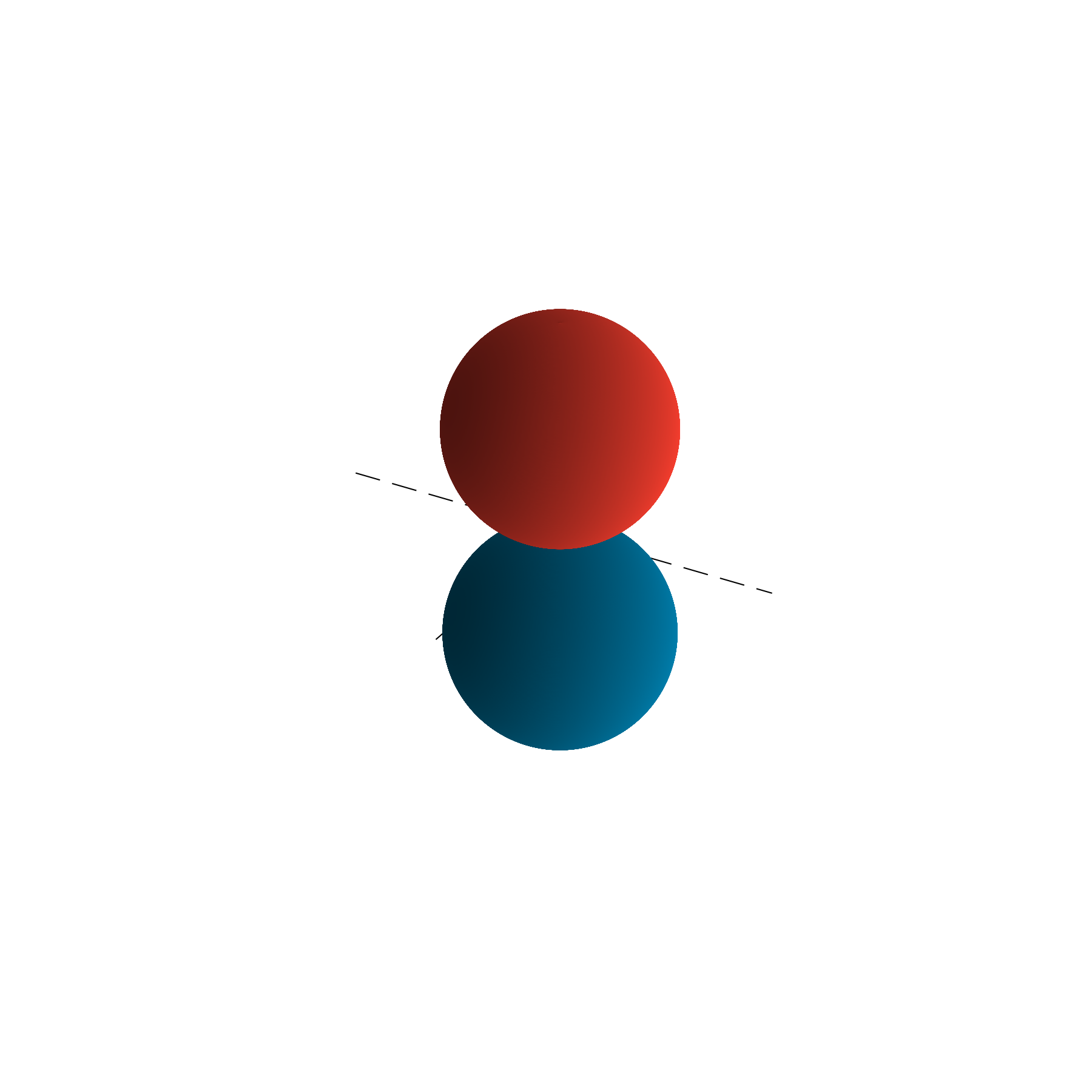
In this mode there is a nodal circle (a circle in which the amplitude of the oscillation is zero), and it can be visualized thinking to a shell in which air move from top to bottom but a circle around the equator stay fixed, and if above is considered positive amplitude, then below the amplitude is negative.
\ell=1 and m=1 has the form:

Is is the same type of oscillation, but this time rather than rotating around the equator is now rotating around the poles.
This is a general pattern: \ell gives the number of the nodal circles, and m the numbers that goes through the poles.
\ell=1 and m=-1 would have the same form rotating around the poles but rotation would be inverting the x and y axis.
\ell=2 and m=0 has the form:

Because \ell=2, there are two nodal circles, and none go through the pole; it can be visualized as squeezing a balloon from the top and the bottom and the same time, and the balloon move sideways.
\ell=2 and m=1 has the form:

In this case too there are two nodal circles, one around the equator and another around the poles, so in this mode adjacent quadrants go in opposite directions.
\ell=2 and m=2 has the form:

which is the same oscillation as the case \ell=2 and m=1 but rotated 90^\circ, in this case as well adjacent quadrants go in opposite directions.