Quantum mechanics angular momentum
In classical mechanics, rotational motion, such as that of a moon circling a planet, embodies the concept of angular momentum. This principle extends to subatomic particles, although electrons in hydrogen atoms do not follow classical orbits around nuclei. The concept of angular momentum remains crucial in quantum mechanics. Before exploring quantum angular momentum, let’s first review its classical counterpart.
Classical Mechanics Angular Momentum
Angular Momentum Eigenfunctions
Total Angular Momentum Operator
Total Angular Momentum Eigenfunctions
Spherical Harmonics Visualization
Classical mechanics angular momentum
The classical angular momentum \mathbf{L} of a small object with linear momentum \mathbf{p}, positioned at a point defined by the position vector \mathbf{r} relative to the origin of our coordinate system, is described by the cross product of \mathbf{r} and \mathbf{p}. This results in \mathbf{L} = \mathbf{r} \times \mathbf{p}, where \mathbf{L} is perpendicular to both \mathbf{r} and \mathbf{p}. Although angular momentum is commonly associated with circular motion, it’s noteworthy that even objects moving in a straight line possess angular momentum relative to a chosen origin. In circular motion, \mathbf{L} = \mathbf{r} \times \mathbf{p} serves as a constant of motion.
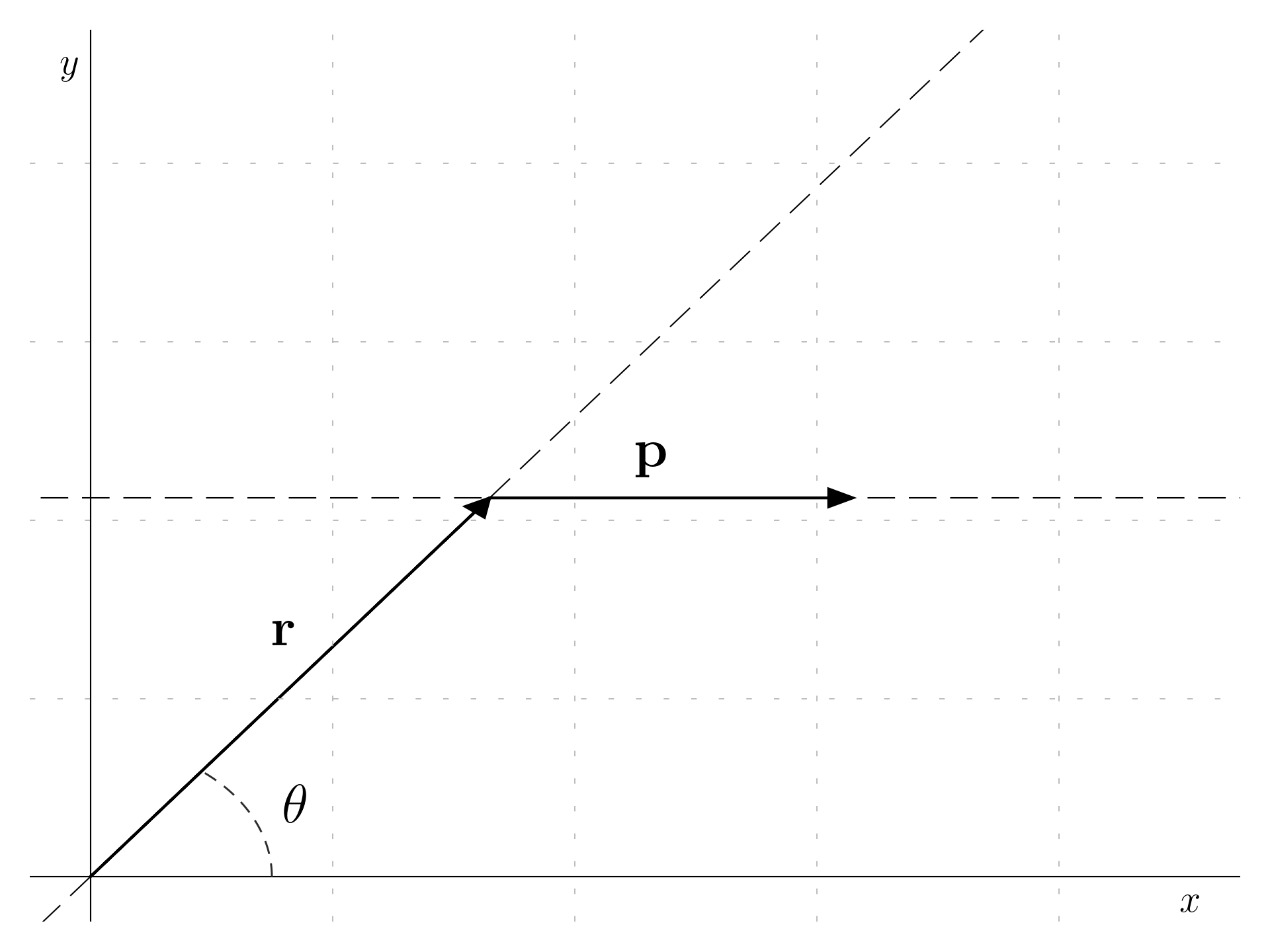
The angular momentum \mathbf{L} can be computed using the determinant of a matrix with the unit vectors \hat{i}, \hat{j}, \hat{k} as the first row, the components of the position vector \mathbf{r} as the second row, and the components of the momentum vector \mathbf{p} as the third row. The formula is given by:
\mathbf{L} = \mathbf{r} \times \mathbf{p} = \hat{c}r\,p\sin(\theta)= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ r_x & r_y & r_z \\ p_x & p_y & p_z \end{vmatrix}
This results in:
\mathbf{L} = (r_y p_z - r_z p_y) \hat{i} - (r_x p_z - r_z p_x) \hat{j} + (r_x p_y - r_y p_x) \hat{k}
The resulting vector (the unitary vector \hat{c} multiplied by the modulus of the two vector and the sine of the angle \theta) is perpendicular to the plane of the two vectors, so, for example, if the vectors are in the xy plane, the angular momentum points to the z direction.
Angular momentum definition
We propose a quantum mechanical angular momentum operator, denoted as \mathbf{L}, by substituting the classical position and momentum with their respective quantum operators. In this framework, the classical position coordinates are replaced by their equivalent quantum position operators. However, for momentum, the quantum mechanical momentum operators are distinct and expressed as -i \hbar \nabla, where \nabla is the gradient operator.
The quantum angular momentum operator \mathbf{L} is defined by the cross product of the position operator vector and the momentum operator vector. In the position representation, the position operator coincides with the position vector, but the momentum operator is given by -i \hbar \nabla. This formulation leads to the expression of \mathbf{L} as:
\mathbf{L} = \mathbf{r} \times (-i \hbar \nabla)
The component operators of angular momentum, \mathbf{L}_x, \mathbf{L}_y, and \mathbf{L}_z, are derived similarly. For instance, the \mathbf{L}_x component is:
\begin{aligned} \mathbf{L}_x & = y \left(-i \hbar \frac{\partial}{\partial z}\right) - z \left(-i \hbar \frac{\partial}{\partial y}\right) \\ & = -i \hbar \left((y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y}\right) \end{aligned}
Analogously, the expressions for \mathbf{L}_y and \mathbf{L}_z are:
\begin{aligned} & \mathbf{L}_y = -i \hbar \left(z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z}\right) \\ & \mathbf{L}_z = -i \hbar \left(x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x}\right) \end{aligned}
It is possible too prove that \mathbf{L}_x is Hermitian, we need to show that \mathbf{L}_x^\dagger = \mathbf{L}_x, where \dagger denotes the Hermitian conjugate (complex conjugate transpose) operation. The \mathbf{L}_x operator is given by:
\mathbf{L}_x = -i \hbar \left( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \right)
The Hermitian conjugate of an operator involves taking the complex conjugate and transposing the order of multiplication. For derivatives, transposition implies applying the derivative to the left instead of the right. The complex conjugate of -i is i, so:
\mathbf{L}_x^\dagger = i \hbar \left( \frac{\partial}{\partial z} y - \frac{\partial}{\partial y} z \right)
Applying integration by parts for the derivative operators acting to the left on a wave function \psi and considering the boundary conditions that wave functions vanish at infinity, we can move the derivatives from acting on the left to acting on the right without changing the sign. This operation effectively restores the original order of multiplication and replaces i with -i, yielding:
\mathbf{L}_x^\dagger = -i \hbar \left( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \right) = \mathbf{L}_x
It can be concluded that \mathbf{L}_x is Hermitian. Each of these operators is Hermitian, and consequently, the composite operator \mathbf{L} is also Hermitian, being a sum of Hermitian components. These operators follow specific commutation relations:
\begin{aligned} & [\mathbf{L}_x, \mathbf{L}_y] = i \hbar \mathbf{L}_z \\ & [\mathbf{L}_y, \mathbf{L}_z] = i \hbar \mathbf{L}_x \\ & [\mathbf{L}_z, \mathbf{L}_x] = i \hbar \mathbf{L}_y \end{aligned}
For example, the commutator [\mathbf{L}_x, \mathbf{L}_y] is defined as \mathbf{L}_x\mathbf{L}_y - \mathbf{L}_y\mathbf{L}_x. Substituting the expressions for \mathbf{L}_x and \mathbf{L}_y gives:
[\mathbf{L}_x, \mathbf{L}_y] = (-i \hbar)^2 \left[ \left( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \right)\left( z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z} \right) - \left( z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z} \right)\left( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \right) \right]
Expanding the brackets and simplifying, we consider the action of partial derivatives:
[\mathbf{L}_x, \mathbf{L}_y] = (-i \hbar)^2 \left[ yz \frac{\partial^2}{\partial z \partial x} - yx \frac{\partial^2}{\partial z^2} - z^2 \frac{\partial^2}{\partial y \partial x} + zx \frac{\partial^2}{\partial y \partial z} - zy \frac{\partial^2}{\partial x \partial z} + z^2 \frac{\partial^2}{\partial x \partial y} + xy \frac{\partial^2}{\partial z^2} - xz \frac{\partial^2}{\partial y \partial z} \right]
Noting that mixed partial derivatives are equal (\frac{\partial^2}{\partial a \partial b} = \frac{\partial^2}{\partial b \partial a}) and terms cancel out, we are left with:
[\mathbf{L}_x, \mathbf{L}_y] = (-i \hbar)^2 \left[ - zx \frac{\partial^2}{\partial y \partial z} + zy \frac{\partial^2}{\partial x \partial z} \right]
Since (-i \hbar)^2 = -\hbar^2, and considering the action of derivatives, we introduce the missing i factor from the definition of \mathbf{L}_z:
[\mathbf{L}_x, \mathbf{L}_y] = i \hbar (-i \hbar) \left[ x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x} \right]
Recognizing the expression in the bracket as \mathbf{L}_z:
[\mathbf{L}_x, \mathbf{L}_y] = i \hbar \mathbf{L}_z
The commutation relations among the angular momentum operators indicate that these operators generally do not share identical eigenfunctions due to their non-commutative nature. This can be easily deduced algebraically from the previously derived expressions.
It is possible to summarize the commutation relations of the angular momentum components in a concise form by stating that the cross product of the angular momentum operator with itself equals i \hbar times the angular momentum operator:
\mathbf L \times \mathbf L = i\hbar \mathbf L
Unlike the position and momentum operators, which can commute under certain conditions allowing for well-defined positions or momenta in multiple directions simultaneously, the components of the angular momentum operator do not commute. As a result, it is impossible for a particle to possess simultaneously well-defined values of angular momentum in more than one direction. This highlights a fundamental difference in the behavior of angular momentum in quantum mechanics compared to classical mechanics, where such constraints do not exist.
Angular momentum in spherical coordinates
Using spherical coordinates and the definition of change of coordinates (for example for x but similar for y and z:
\frac{\partial}{\partial x} = \frac{\partial r}{\partial x}\frac{\partial}{\partial r} + \frac{\partial \theta}{\partial x}\frac{\partial}{\partial \theta} + \frac{\partial \phi}{\partial x}\frac{\partial}{\partial \phi}
To derive the expression for the angular momentum operator \mathbf L_x in spherical polar coordinates (r, \theta, \phi), we start from its definition in Cartesian coordinates and transform it into spherical coordinates. In Cartesian coordinates, \mathbf L_x is given by:
\mathbf {L}_x = -i\hbar \left(y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y}\right)
Applying the partial derivatives in spherical coordinates with the chain rule:
\begin{aligned} & \frac{\partial}{\partial y} = \frac{\partial r}{\partial y}\frac{\partial}{\partial r} + \frac{\partial \theta}{\partial y}\frac{\partial}{\partial \theta} + \frac{\partial \phi}{\partial y}\frac{\partial}{\partial \phi} \\ & \frac{\partial}{\partial z} = \frac{\partial r}{\partial z}\frac{\partial}{\partial r} + \frac{\partial \theta}{\partial z}\frac{\partial}{\partial \theta} + \frac{\partial \phi}{\partial z}\frac{\partial}{\partial \phi} \end{aligned}
Given:
\begin{aligned} & \frac{\partial r}{\partial y} = \frac{y}{r}, \quad \frac{\partial \theta}{\partial y} = \frac{x}{r^2 \sin(\theta)}, \quad \frac{\partial \phi}{\partial y} = \frac{\cos(\phi)}{r \sin(\theta)}\\ & \frac{\partial r}{\partial z} = \frac{z}{r}, \quad \frac{\partial \theta}{\partial z} = -\frac{\sqrt{x^2 + y^2}}{r^2} = -\frac{\sin(\theta)}{r}, \quad \frac{\partial \phi}{\partial z} = 0 \end{aligned}
Substituting these into the expressions for \mathbf L_x, we get:
\mathbf {L}_x = -i\hbar \left[ \left( r \sin(\theta) \sin(\phi) \right) \left( -\frac{\sin(\theta)}{r} \frac{\partial}{\partial \theta} \right) - \left( r \cos(\theta) \right) \left( \frac{\cos(\phi)}{r \sin(\theta)} \frac{\partial}{\partial \phi} \right) \right]
Simplifying, we find:
\mathbf {L}_x = -i\hbar \left( -\sin(\phi) \frac{\partial}{\partial \theta} - \cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi} \right)
The \mathbf L_x operator in spherical coordinates is:
\mathbf {L}_x = i\hbar \left( \sin(\phi) \frac{\partial}{\partial \theta} + \cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi} \right)
To derive the expression for the angular momentum operator \mathbf L_y:
\mathbf {L}_y = -i\hbar \left(z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z}\right)
Applying the partial derivatives in spherical coordinates with the chain rule:
\begin{aligned} & \frac{\partial}{\partial x} = \frac{\partial r}{\partial x}\frac{\partial}{\partial r} + \frac{\partial \theta}{\partial x}\frac{\partial}{\partial \theta} + \frac{\partial \phi}{\partial x}\frac{\partial}{\partial \phi} \\ & \frac{\partial}{\partial z} = \frac{\partial r}{\partial z}\frac{\partial}{\partial r} + \frac{\partial \theta}{\partial z}\frac{\partial}{\partial \theta} + \frac{\partial \phi}{\partial z}\frac{\partial}{\partial \phi} \end{aligned}
With the relevant derivatives being:
\begin{aligned} & \frac{\partial r}{\partial x} = \frac{x}{r}, \quad \frac{\partial \theta}{\partial x} = \frac{y}{r^2 \sin(\theta)}, \quad \frac{\partial \phi}{\partial x} = -\frac{\sin(\phi)}{r \sin(\theta)} \\ & \frac{\partial r}{\partial z} = \frac{z}{r}, \quad \frac{\partial \theta}{\partial z} = -\frac{\sin(\theta)}{r}, \quad \frac{\partial \phi}{\partial z} = 0 \end{aligned}
Substituting these into the expression for \mathbf L_y yields:
\mathbf {L}_y = -i\hbar \left[ \left( r \cos(\theta) \right) \left( \frac{x}{r} \frac{\partial}{\partial r} + \frac{y}{r^2 \sin(\theta)} \frac{\partial}{\partial \theta} - \frac{\sin(\phi)}{r \sin(\theta)} \frac{\partial}{\partial \phi} \right) - \left( r \sin(\theta) \cos(\phi) \right) \left( -\frac{\sin(\theta)}{r} \frac{\partial}{\partial \theta} \right) \right]
Simplifying, and focusing on the relevant terms for \mathbf L_y, we find:
\mathbf {L}_y = i\hbar \left( -\cos(\phi) \frac{\partial}{\partial \theta} + \cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi} \right)
Therefore, the \mathbf L_y operator in spherical coordinates is:
\mathbf {L}_y = i\hbar \left( -\cos(\phi) \frac{\partial}{\partial \theta} + \cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi} \right)
For \mathbf L_z in spherical polar coordinates, the transformation from Cartesian coordinates is more straightforward due to the alignment of the z-axis with the polar axis in spherical coordinates. The angular momentum component \mathbf L_z in Cartesian coordinates is given by:
\mathbf {L}_z = -i\hbar \left(x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x}\right)
To transform the \mathbf L_z angular momentum component from Cartesian to spherical polar coordinates using the chain rule formula for derivatives, we start by acknowledging the \mathbf L_z operator in Cartesian coordinates:
\mathbf {L}_z = -i\hbar\left(x\frac{\partial}{\partial y} - y\frac{\partial}{\partial x}\right)
Applying the partial derivatives in spherical coordinates with the chain rule:
\begin{aligned} & \frac{\partial}{\partial x} = \frac{\partial r}{\partial x}\frac{\partial}{\partial r} + \frac{\partial \theta}{\partial x}\frac{\partial}{\partial \theta} + \frac{\partial \phi}{\partial x}\frac{\partial}{\partial \phi} \\ & \frac{\partial}{\partial y} = \frac{\partial r}{\partial y}\frac{\partial}{\partial r} + \frac{\partial \theta}{\partial y}\frac{\partial}{\partial \theta} + \frac{\partial \phi}{\partial y}\frac{\partial}{\partial \phi} \end{aligned}
With the relevant derivatives being:
\begin{aligned} & \frac{\partial r}{\partial x} = \frac{x}{r}, \quad \frac{\partial \theta}{\partial x} = \frac{y}{r^2 \sin(\theta)}, \quad \frac{\partial \phi}{\partial x} = -\frac{\sin(\phi)}{r \sin(\theta)} \\ & \frac{\partial r}{\partial y} = \frac{y}{r}, \quad \frac{\partial \theta}{\partial y} = \frac{x}{r^2 \sin(\theta)}, \quad \frac{\partial \phi}{\partial y} = \frac{\cos(\phi)}{r \sin(\theta)} \end{aligned}
Substituting these into the expression for \mathbf L_z gives:
\mathbf {L}_z = -i\hbar \left( x \left( \frac{\cos(\phi)}{r \sin(\theta)} \right) - y \left( -\frac{\sin(\phi)}{r \sin(\theta)} \right) \right) \frac{\partial}{\partial \phi}
Simplifying the expression using the relationships for x and y in spherical coordinates, we recognize that the x and y components combine to simply give a derivative with respect to \phi:
\mathbf {L}_z = -i\hbar \left( \cos^2(\phi) + \sin^2(\phi) \right) \frac{\partial}{\partial \phi} = -i\hbar \frac{\partial}{\partial \phi}
Angular momentum eigenfunctions
For the eigenvalues computation, using the expression for \mathbf L_z:
\mathbf {L}_z = -i\hbar \frac{\partial}{\partial \phi}
It is possible to write an eigenequation of the form:
\mathbf {L}_z \Phi(\phi) = m\hbar \Phi(\phi)
A function of the form:
\Phi(\phi) = e^{i\hbar\phi}
is a solution of this equation; however the requirement that the wave function and its derivative are continuous after a complete round of 2 \pi means that the number m must be an integer (m \in \mathbb Z). Then, the angular momentum is quantized around the z axis, with units of angular momentum \hbar.
The eigenfunctions corresponding to the angular momentum operators for the x, y, and z axes, \mathbf L_x, \mathbf L_y, and \mathbf L_z are different. This difference is expected due to the non-commutativity of these operators. The derivation was done with the choice of the z-axis as reference, selecting the x or y-axis would yield eigenfunctions for \mathbf L_x and \mathbf L_y that are analogous to those for \mathbf L_z, just based on rotation angles about the respective axes. Thus, while the eigenfunctions for \mathbf L_x, \mathbf L_y, and \mathbf L_z differ, understanding each set of eigenfunctions is straightforward, reflecting the axes’ symmetry and the angular momentum operators’ mathematical properties.
Total angular momentum operator
The operator \mathbf{L}^2 represents the “dot” product of the angular momentum operator \mathbf{L} with itself, defined as \mathbf{L}_x^2 + \mathbf{L}_y^2 + \mathbf{L}_z^2. Here, \mathbf{L}_x^2 means \mathbf{L}_x operating on \mathbf{L}_x, and similarly for \mathbf{L}_y^2 and \mathbf{L}_z^2.
I can be derived from the expression in polar coordinates.
Starting from \mathbf L_x^2:
\begin{aligned} \mathbf {L}_x^2 =& -\hbar^2 \left( \sin(\phi) \frac{\partial}{\partial \theta} + \cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi} \right)^2 \\ = & -\hbar^2 \left(\sin^2(\phi) \frac{\partial^2}{\partial \theta^2} + \sin(\phi) \frac{\partial}{\partial \theta}\left[\cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi}\right] + \cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi}\left[\sin(\phi) \frac{\partial}{\partial \theta}\right] + \cot^2(\theta) \cos^2(\phi) \frac{\partial^2}{\partial \phi^2} \right) \\ = & -\hbar^2 \left(\sin^2(\phi) \frac{\partial^2}{\partial \theta^2} - \sin(\phi) \csc^2(\theta) \cos(\phi) \frac{\partial}{\partial \phi} + \cot(\theta) \cos^2(\phi) \frac{\partial}{\partial \theta} \right. \\ & \left. + 2\sin(\phi)\cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi}\frac{\partial}{\partial \theta} + \cot^2(\theta) \cos^2(\phi) \frac{\partial^2}{\partial \phi^2} \right) \end{aligned}
Then \mathbf L_y^2:
\begin{aligned} \mathbf {L}_y^2 & = i\hbar \left( -\cos(\phi) \frac{\partial}{\partial \theta} + \cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi} \right)^2 \\ = & -\hbar^2 \left(\cos^2(\phi) \frac{\partial^2}{\partial \theta^2} - \cos(\phi) \frac{\partial}{\partial \theta}\left[\cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi}\right] - \cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi}\left[\cos(\phi) \frac{\partial}{\partial \theta}\right] + \cot^2(\theta) \sin^2(\phi) \frac{\partial^2}{\partial \phi^2} \right) \\ = & -\hbar^2 \left(\cos^2(\phi) \frac{\partial^2}{\partial \theta^2} + \cos(\phi) \csc^2(\theta) \sin(\phi) \frac{\partial}{\partial \phi} + \cot(\theta) \sin^2(\phi) \frac{\partial}{\partial \theta} \right. \\ & \left.- 2\cos(\phi)\cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi}\frac{\partial}{\partial \theta} + \cot^2(\theta) \sin^2(\phi) \frac{\partial^2}{\partial \phi^2} \right) \end{aligned}
Finally \mathbf L_z^2:
\mathbf L_z^2 = -\hbar^2 \frac{\partial^2}{\partial \phi^2}
Summing to compute \ell^2:
\begin{aligned} L^2 = & \mathbf{L}_x^2 + \mathbf{L}_y^2 + \mathbf{L}_z^2 \\ = & -\hbar^2 \left(\sin^2(\phi) \frac{\partial^2}{\partial \theta^2} - \sin(\phi) \csc^2(\theta) \cos(\phi) \frac{\partial}{\partial \phi} + \cot(\theta) \cos^2(\phi) \frac{\partial}{\partial \theta} \right. \\ & \left. + 2\sin(\phi)\cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi}\frac{\partial}{\partial \theta} + \cot^2(\theta) \cos^2(\phi) \frac{\partial^2}{\partial \phi^2} \right.\\ & +\left.\cos^2(\phi) \frac{\partial^2}{\partial \theta^2} + \cos(\phi) \csc^2(\theta) \sin(\phi) \frac{\partial}{\partial \phi} + \cot(\theta) \sin^2(\phi) \frac{\partial}{\partial \theta} \right. \\ & \left.- 2\cos(\phi)\cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi}\frac{\partial}{\partial \theta} + \cot^2(\theta) \sin^2(\phi) \frac{\partial^2}{\partial \phi^2} \right. \\ & \left. + \frac{\partial^2}{\partial \phi^2} \right) \\ = & -\hbar^2 \left(\left [\sin^2(\phi) +\cos^2(\phi) \right] \frac{\partial^2}{\partial \theta^2} + \left[ - \sin(\phi) \csc^2(\theta) \cos(\phi) \frac{\partial}{\partial \phi} + \cos(\phi) \csc^2(\theta) \sin(\phi) \frac{\partial}{\partial \phi} \right] \right. \\ & + \left. \left[ 2\sin(\phi)\cot(\theta) \cos(\phi) \frac{\partial}{\partial \phi}\frac{\partial}{\partial \theta} - 2\cos(\phi)\cot(\theta) \sin(\phi) \frac{\partial}{\partial \phi}\frac{\partial}{\partial \theta} \right] \right.\\ & + \left. \cot(\theta) \left[ \cos^2(\phi) + \sin^2(\phi) \right]\frac{\partial}{\partial \theta} \right.\\ & + \left. \cot^2(\theta) \left[ \cos^2(\phi) + \sin^2(\phi) \right] \frac{\partial^2}{\partial \phi^2} + \frac{\partial^2}{\partial \phi^2} \right) \\ & = -\hbar^2 \left(\frac{\partial^2}{\partial \theta^2} + \cot(\theta)\frac{\partial}{\partial \theta} + \left(\cot^2(\theta) + 1\right) \frac{\partial^2}{\partial \phi^2} \right)\\ & = -\hbar^2 \left(\frac{\partial^2}{\partial \theta^2} + \cot(\theta)\frac{\partial}{\partial \theta} + \frac{1}{\sin^2(\theta)} \frac{\partial^2}{\partial \phi^2} \right) \\ & = -\hbar^2 \left(\frac{1}{\sin(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta)\frac{\partial}{\partial \theta}\right) + \frac{1}{\sin^2(\theta)} \frac{\partial^2}{\partial \phi^2} \right) \end{aligned}
Since the Laplacian in polar coordinates is:
\nabla^2 = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2 \frac{\partial}{\partial r}\right) + \frac{1}{r^2\sin\theta}\left[\frac{\partial}{\partial \theta}\left(\sin\theta \frac{\partial}{\partial \theta}\right) + \frac{\partial^2}{\partial \phi^2}\right]
The above can be written as:
L^2 = -\hbar^2 \nabla^2_{\theta,\phi}
where:
\nabla^2_{\theta,\phi} = \left(\frac{1}{\sin(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta)\frac{\partial}{\partial \theta}\right) + \frac{1}{\sin^2(\theta)} \frac{\partial^2}{\partial \phi^2} \right)
is the \theta and \phi part of the Laplacian operator.
It is possible to show that \nabla^2_{\theta,\phi} commutes with \mathbf L_z.
Applying \nabla^2_{\theta,\phi} to \mathbf L_z = -i\hbar\frac{\partial}{\partial \phi}, we focus only on the \phi-dependent part since \mathbf L_z does not affect \theta-dependent terms:
\nabla^2_{\theta,\phi} L_z = \nabla^2_{\theta,\phi} \left(-i\hbar\frac{\partial}{\partial \phi}\right) = \left(\frac{1}{\sin^2(\theta)} \frac{\partial^2}{\partial \phi^2}\right) \left(-i\hbar\frac{\partial}{\partial \phi}\right) = -i\hbar \frac{1}{\sin^2(\theta)} \frac{\partial^3}{\partial \phi^3}
Applying \mathbf L_z to \nabla^2_{\theta,\phi}, we again focus on the \phi-dependent part:
L_z \nabla^2_{\theta,\phi} = -i\hbar\frac{\partial}{\partial \phi} \left(\frac{1}{\sin^2(\theta)} \frac{\partial^2}{\partial \phi^2} \right) = -i\hbar \frac{1}{\sin^2(\theta)} \frac{\partial^3}{\partial \phi^3}
The commutator of \nabla^2_{\theta,\phi} and \mathbf L_z is given by:
\left[\nabla^2_{\theta,\phi}, L_z\right] = \nabla^2_{\theta,\phi} L_z - L_z \nabla^2_{\theta,\phi}
Substituting the above computations, we find:
\left[\nabla^2_{\theta,\phi}, L_z\right] = -i\hbar \frac{1}{\sin^2(\theta)} \frac{\partial^3}{\partial \phi^3} - \left(-i\hbar \frac{1}{\sin^2(\theta)} \frac{\partial^3}{\partial \phi^3}\right) = 0
This shows that \nabla^2_{\theta,\phi} and \mathbf L_z commute.
The selection of the z direction in defining \mathbf{L}^2 is completely arbitrary. One could have chosen the polar axis along the x direction or the y direction as well. In such cases, it would be equally evident that \mathbf{L}^2 commutes with \mathbf{L}_x or \mathbf{L}_y, respectively. The peculiar aspect is that while \mathbf{L}^2 can commute with each of \mathbf{L}_x, \mathbf{L}_y, and \mathbf{L}_z individually, the operators \mathbf{L}_x, \mathbf{L}_y, and \mathbf{L}_z do not commute among themselves. This is resolved by the possibility of aligning the eigenfunctions of \mathbf{L}^2 with any one set of eigenfunctions from \mathbf{L}_x, \mathbf{L}_y, or \mathbf{L}_z.
Total angular momentum eigenfunctions
To find the eigenfunction of the operator, the equation to solve is the equation:
\nabla^2_{\theta,\phi}Y(\theta,\phi) = -\ell(\ell+1) Y(\theta,\phi)
The assumption for solving this equation is to apply the separation of variables technique, looking for a solution of type:
Y(\theta,\phi) = \Theta(\theta)\Phi(\phi)
Substituting into the equation, it gives:
\frac{\Phi(\phi)}{\sin(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta)\frac{\partial}{\partial \theta}\right)\Theta(\theta) + \frac{\Theta(\theta)}{\sin^2(\theta)} \frac{\partial^2\Phi(\phi)}{\partial \phi^2} = -\ell(\ell+1)\Theta(\theta)\Phi(\phi)
Multiplying by:
\frac{\sin^2(\theta)}{\Theta(\theta)\Phi(\phi)}
and rearranging:
\frac{1}{\Phi(\phi)} \frac{\partial^2\Phi(\phi)}{\partial \phi^2} = -\ell(\ell+1)\sin^2(\theta) - \frac{\sin(\theta)}{\Theta(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta)\frac{\partial}{\partial \theta}\right)\Theta(\theta)
Since the left hand side only depends on \phi, and the right hand side only depends on \theta, then they must both be equal to a separation constant -m^2 (the square is chosen to avoid a \sqrt c coefficient from the \phi solution, and the minus for the sign).
\frac{1}{\Phi(\phi)} \frac{\partial^2\Phi(\phi)}{\partial \phi^2} = -m^2
The solution could be any combination of \cos(m\phi), \sin(m\phi), e^{m\phi}. The latter will be chosen because it is also a solution for the \mathbf L_z eigenequation:
\mathbf L_z \Phi(\phi) = m\hbar \Phi(\phi)
Since the derivatives need to be continuous and this is a periodic function, it means that m must be an integer.
For the right hand side:
\lambda\sin^2(\theta) - \frac{\sin(\theta)}{\Theta(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta)\frac{\partial}{\partial \theta}\right)\Theta(\theta) = -m^2
multiplying by \frac{\Theta(\theta)}{\sin^2(\theta)} and rearranging:
\frac{1}{\sin(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta)\frac{\partial}{\partial \theta}\right)\Theta(\theta) -m^2 \frac{\Theta(\theta)}{\sin^2(\theta)} - -\ell(\ell+1)\Theta(\theta) = 0
Setting x = \cos(\theta). Given the equation:
\frac{1}{\sin(\theta)}\frac{\partial}{\partial \theta}\left(\sin(\theta)\frac{\partial \Theta}{\partial \theta}\right) - \frac{m^2 \Theta(\theta)}{\sin^2(\theta)} + l(l+1)\Theta(\theta) = 0
Let x = \cos(\theta), then \sin(\theta) = \sqrt{1-x^2} and \frac{dx}{d\theta} = -\sin(\theta).
The first term becomes:
\frac{d}{d\theta}\left(\sin(\theta)\frac{d\Theta}{d\theta}\right) = \frac{d}{dx}\left(\sqrt{1-x^2}\frac{d\Theta}{dx}\right)\frac{dx}{d\theta} = -\sqrt{1-x^2}\frac{d}{dx}\left(\sqrt{1-x^2}\frac{d\Theta}{dx}\right)
Expanding and simplifying, we obtain the Legendre differential equation in the form:
(1-x^2)\frac{d^2\Theta}{dx^2} - 2x\frac{d\Theta}{dx} + \left[\ell(\ell+1) - \frac{m^2}{1-x^2}\right]\Theta = 0
This is the associated Legendre differential equation for integer values of \ell and m, where x = \cos(\theta). When m = 0, it reduces to the Legendre differential equation:
(1-x^2)\frac{d^2\Theta}{dx^2} - 2x\frac{d\Theta}{dx} + \ell(\ell+1)\Theta = 0
The solutions of these equations are the associated Legendre functions that can be written as:
\Theta(\theta) = P^m_\ell(\cos(\theta))
These solution requires that \ell \in \mathbb N and -ell \le m \le \ell.
The Rodrigues’ formula for the associated Legendre polynomials P_\ell^m(x) is given by:
P_\ell^m(x) = (-1)^m(1-x^2)^{m/2}\frac{d^m}{dx^m}P_\ell(x)
where P_\ell(x) is the Legendre polynomial of degree \ell, and it can be expressed as:
P_\ell(x) = \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2-1)^l
Combining these, the complete formula for P_\ell^m(x) becomes:
P_\ell^m(x) = (-1)^m(1-x^2)^{m/2}\frac{1}{2^l l!}\frac{d^{l+m}}{dx^{l+m}}(x^2-1)^l
The first few associated Legendre polynomials are:
\begin{aligned} P_0^0(x) &= 1\\ P_1^0(x) &= x \\ P_1^1(x) &= -\sqrt{1-x^2} \\ P_2^0(x) &= \frac{1}{2}(3x^2-1) \\ P_2^1(x) &= -3x\sqrt{1-x^2} \\ P_2^2(x) &= 3(1-x^2) \\ P_3^0(x) &= \frac{1}{2}(5x^3-3x) \\ P_3^1(x) &= -\frac{3}{2}(5x^2-1)\sqrt{1-x^2} \\ P_3^2(x) &= 15x(1-x^2) \\ P_3^3(x) &= -15(1-x^2)\sqrt{1-x^2} \\ P_4^0(x) &= \frac{1}{8}(35x^4-30x^2+3) \\ P_4^1(x) &= -\frac{5}{2}(7x^3-3x)\sqrt{1-x^2} \\ P_4^2(x) &= \frac{15}{2}(7x^2-1)(1-x^2) \\ P_4^3(x) &= -105x(1-x^2)\sqrt{1-x^2} \\ P_4^4(x) &= 105(1-x^2)^2 \\ P_5^0(x) &= \frac{1}{8}(63x^5-70x^3+15x) \\ P_5^1(x) &= -\frac{15}{8}(21x^4-14x^2+1)\sqrt{1-x^2} \\ P_5^{-1}(x) &= \frac{15}{8}(21x^4-14x^2+1)\sqrt{1-x^2} \end{aligned}
These function have the following properties:
- the highest power of the argument x is always x^\ell;
- the version with -m and m are the same function other than a prefactor;
- in the open interval (-1,1) (excluding therefore these points) they have \ell - |m| zeros;
Replacing x =\cos(\theta) and using trigonometric identities:
\begin{aligned} P_0^0(\cos(\theta)) &= 1\\ P_1^0(\cos(\theta)) &= \cos(\theta) \\ P_1^1(\cos(\theta)) &= -\sin(\theta) \\ P_2^0(\cos(\theta)) &= \frac{1}{2}(3\cos^2(\theta)-1) \\ P_2^1(\cos(\theta)) &= -3\cos(\theta)\sin(\theta) \\ P_2^2(\cos(\theta)) &= 3\sin^2(\theta) \\ P_3^0(\cos(\theta)) &= \frac{1}{2}(5\cos^3(\theta)-3\cos(\theta)) \\ P_3^1(\cos(\theta)) &= -\frac{3}{2}\sin(\theta)(5\cos^2(\theta)-1) \\ P_3^2(\cos(\theta)) &= 15\cos(\theta)\sin^2(\theta) \\ P_3^3(\cos(\theta)) &= -15\sin^3(\theta) \\ P_4^0(\cos(\theta)) &= \frac{1}{8}(35\cos^4(\theta)-30\cos^2(\theta)+3) \\ P_4^1(\cos(\theta)) &= -\frac{5}{2}\sin(\theta)(7\cos^3(\theta)-3\cos(\theta)) \\ P_4^2(\cos(\theta)) &= \frac{105}{8}(7\cos^2(\theta)-1)\sin^2(\theta) \\ P_4^3(\cos(\theta)) &= -\frac{105}{2}\cos(\theta)\sin^3(\theta) \\ P_4^4(\cos(\theta)) &= \frac{945}{8}\sin^4(\theta) \\ P_5^0(\cos(\theta)) &= \frac{1}{8}(63\cos^5(\theta)-70\cos^3(\theta)+15\cos(\theta)) \\ P_5^1(\cos(\theta)) &= -\frac{45}{8}\sin(\theta)(21\cos^4(\theta)-14\cos^2(\theta)+1) \\ P_5^{-1}(\cos(\theta)) &= \frac{45}{8}\sin(\theta)(21\cos^4(\theta)-14\cos^2(\theta)+1) \end{aligned}
Then, the eigenequation:
L^2_{\theta,\phi}Y_{\ell,m}(\theta,\phi) = \hbar^2 l(l+1) Y_{\ell,m}(\theta,\phi)
has the solution:
Y_{\ell,m}(\theta,\phi) = \sqrt{\frac{(2l+1)}{4\pi}\frac{(l-m)!}{(l+m)!}}P_\ell^m(\cos\theta)e^{im\phi}, \quad l\in \mathbb N, \quad -l \ge m \ge l
these functions of \theta, \phi are known as the spherical harmonics Y_{\ell,m}(\theta,\phi) and are the eigenfunctions of that equation.
The eigenvalues are:
\hbar^2l(l+1)
The first few spherical harmonic functions Y_{\ell,m}(\theta, \phi) for \ell = 0, 1, 2, 3, expressed in terms of the associated Legendre polynomials P_\ell^m(\cos\theta) and the angular functions e^{im\phi} are:
| \ell | m | Y_{\ell,m}(\theta, \phi) |
|---|---|---|
| 0 | 0 | \sqrt{\frac{1}{4\pi}} |
| 1 | 0 | \sqrt{\frac{3}{4\pi}}\cos\theta |
| \pm 1 | \mp\sqrt{\frac{3}{8\pi}}\sin\theta e^{\pm i\phi} | |
| 2 | 0 | \sqrt{\frac{5}{16\pi}}(3\cos^2\theta - 1) |
| \pm 1 | \mp\sqrt{\frac{15}{8\pi}}\cos\theta\sin\theta e^{\pm i\phi} | |
| \pm 2 | \sqrt{\frac{15}{32\pi}}\sin^2\theta e^{\pm 2i\phi} | |
| 3 | 0 | \sqrt{\frac{7}{16\pi}}(5\cos^3\theta - 3\cos\theta) |
| \pm 1 | \mp\sqrt{\frac{21}{64\pi}}(5\cos^2\theta - 1)\sin\theta e^{\pm i\phi} | |
| \pm 2 | \sqrt{\frac{105}{32\pi}}\cos\theta\sin^2\theta e^{\pm 2i\phi} | |
| \pm 3 | \mp\sqrt{\frac{35}{64\pi}}\sin^3\theta e^{\pm 3i\phi} |
A node (or nodal line/nodal surface) refers to the set of points on the surface of the sphere where the spherical harmonic function equals zero:
- \ell determines the total number of nodal lines, including latitudinal and longitudinal ones.
- |m| influences the number of nodes that pass through the poles, with |m| longitudinal nodes when m \neq 0. For m = 0, there are no nodes passing through the poles.
Spherical harmonics are also eigenfunctions of the \mathbf L_z operator:
\begin{aligned} & \mathbf L_zY(\theta,\phi) = m \hbar Y_{\ell,m}(\theta,\phi) \\ & -i\hbar \frac{\partial}{\partial \phi}\left(\sqrt{\frac{(2\ell+1)}{4\pi}\frac{(\ell-m)!}{(\ell+m)!}}P_\ell^m(\cos\theta)e^{im\phi} \right) = \sqrt{\frac{(2l+1)}{4\pi}\frac{(\ell-m)!}{(\ell+m)!}}P_\ell^m(\cos\theta)e^{im\phi} \end{aligned}
As \mathbf L_z depends only of \phi, it is not depends from any function of \theta.
Spherical harmonics notation
In atomic physics, the terms s, p, d, and f denote specific atomic orbitals distinguished by their angular momentum quantum number, \ell. Historically, these labels were derived from the spectroscopic patterns observed for hydrogen: sharp, principal, diffuse, and fundamental, which correlate with \ell values of 0, 1, 2, and 3, respectively. These terms, while originally descriptive of spectral line appearances, now serve primarily to denote \ell values. The notation extends alphabetically beyond f for higher \ell values, with g for \ell=4, h for \ell=5, and so on:
\begin{array}{ll} \text{s} & \ell=0 \\ \text{p} & \ell=1 \\ \text{d} & \ell=2 \\ \text{f} & \ell=3 \\ \text{g} & \ell=4 \\ \text{h} & \dots \end{array}