Particle and barrier
Having explored the idealized concept of a particle confined within an infinite potential well here, we now turn our attention towards a more realistic scenario within the realm of quantum mechanics: particles encountering potential barriers.
Well with Infinite Tick Barrier
In the context of the Schrödinger equation, when dealing with energy (E), potential (V(x)), and the wave function (\psi(x)) that are all finite, it’s essential that the derivatives of the wave function with respect to position, specifically \frac{\mathrm d\psi(x)}{\mathrm d x} and \frac{\mathrm d^2\psi(x)}{\mathrm d x^2}, remain finite. This requirement stems from the mathematical form and physical interpretation of the Schrödinger equation.
The Schrödinger equation, in one dimension, is given by:
-\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} + V(x)\psi(x) = E\psi(x)
For the equation to hold, each term must be well-defined and finite across the domain of interest.
-
Mathematical Consistency: The wave function \psi(x) must be a smooth, continuous function for its second derivative \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} to exist everywhere (except possibly at points of infinite potential). If the second derivative were not finite, it would imply an infinite kinetic energy, which is not physically meaningful for a bounded system with finite total energy E.
-
Physical Interpretability: The wave function’s square magnitude |\psi(x)|^2 represents the probability density of finding a particle in a given position. For this interpretation to hold, \psi(x) and its derivatives must be finite to avoid non-physical implications like infinite probability densities.
-
Boundary Conditions: The finiteness of \psi(x) and its derivatives ensures that boundary conditions can be properly applied. For instance, in a bounded system, the wave function typically goes to zero at the boundaries. If the derivatives were not finite, matching these boundary conditions and ensuring a physically meaningful solution across the entire domain would be impossible.
Now that these boundary conditions have been identified:
- \psi(x) must be continuous;
- \frac{\mathrm d\psi(x)}{\mathrm d x} must be continuous.
it is possible to solve problems with finite heights of boundaries.
In classical mechanics, the behavior of a ball encountering a barrier or moving along a slope is governed by Newton’s laws of motion, which predict deterministic outcomes based on the initial conditions. For a ball hitting a solid, impenetrable barrier, classical physics states that the ball will bounce back if it lacks sufficient energy to overcome the barrier’s height. Conversely, when rolling down a slope, the ball accelerates due to gravity, with its velocity increasing as it descends.
If the ball has sufficient energy—taking into account its kinetic energy from the descent and any potential energy it started with—it can overcome the gravitational potential energy at the top of another slope or barrier. Should this energy be adequate, the ball will ascend the opposite slope and continue its motion beyond the peak, its trajectory determined by the conservation of energy principle.
These outcomes are rooted in the principles of energy conservation and force interactions, where the future state of the ball can be precisely predicted given its current state and the forces acting upon it.
The ball could not overcame the barrier if the energy would not sufficient and surely cannot be found inside the barrier.
A quantum mechanical particle, however, can be found within the barrier, and can get to the other side of the barrier, even if its energy is less than the height of the potential barrier; this effect is known as tunnelling.
Infinitely tick barrier
Considering a potential V(x) such as:
V(x) = \begin{cases} 0 & \quad x \le 0 \\ V_0 & \quad x > 0 \end{cases}
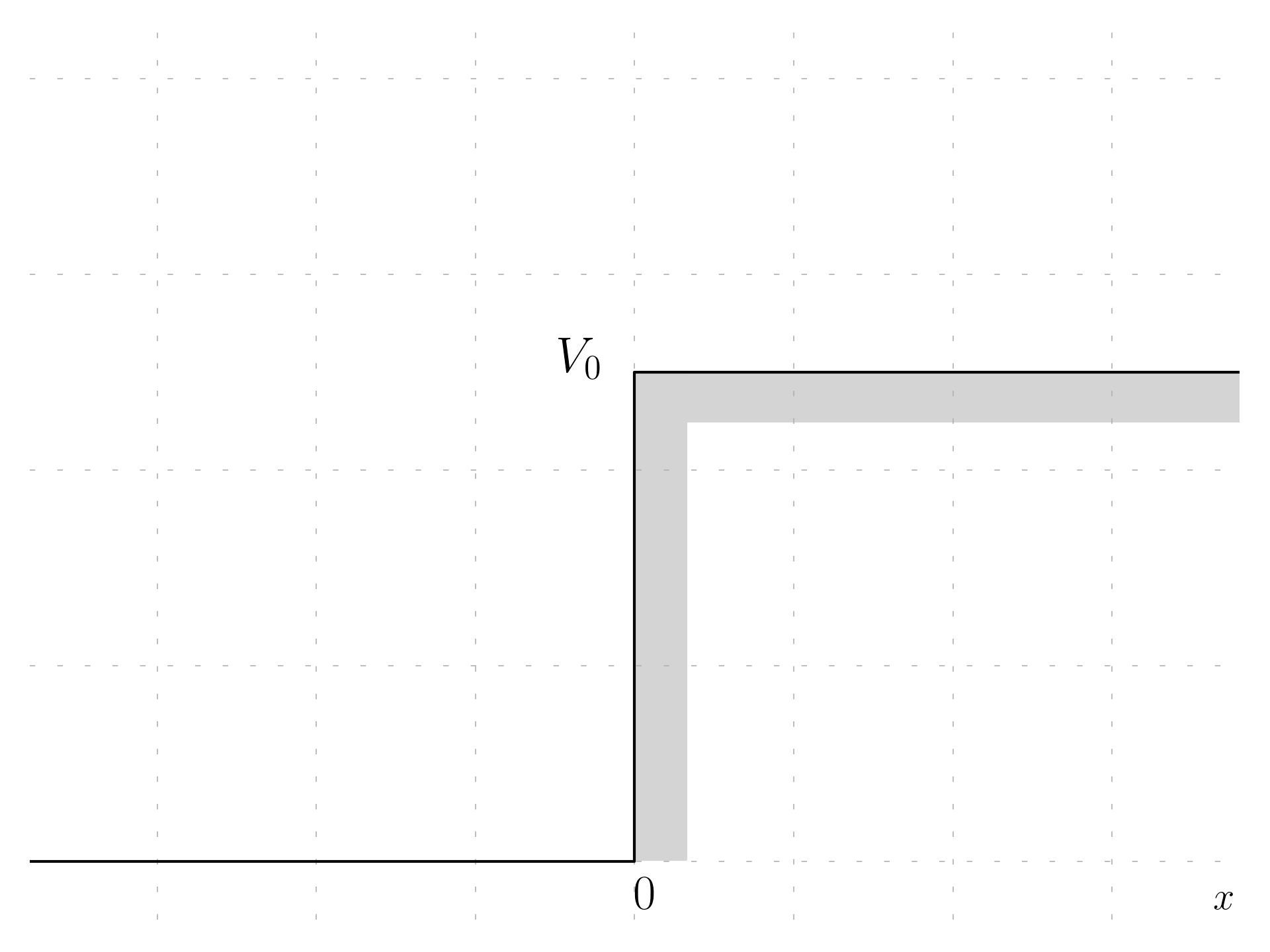
A quantum mechanic wave is incident from the left, and some reflection is allowed on this wall; on this region the solution can be described with complex exponential waves as:
\psi_L(x) = C\,e^{ikx} + D\,e^{-ikx}, \quad k = \sqrt{\frac{2mE}{\hbar^2}}
C\,e^{ikx} is incident wave (going to the right) and D\,e^{-ikx} is the reflected wave (going to the left).
E < V_0
At first, let’s consider an energy which is less than V_0. Inside the barrier, the Schrödinger equation hold (with V_0 - E > 0):
\begin{aligned} & -\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} + V_0\psi(x) = E\psi(x) \\ & \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = \frac{2m}{\hbar^2} \left( V_0 - E \right)\psi(x) \end{aligned}
The solution of this equation can be written as:
\psi_R(x) = F\,e^{\kappa x} + G\,e^{-\kappa x}, \quad \kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}}, \quad \kappa \in \mathbb R
F=0 because otherwise the wave function will be growing exponentially and it won’t be possible to normalize the solution. So the solution will be:
\psi_R(x) = G\,e^{-\kappa x}, \quad \kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}}, \quad \kappa \in \mathbb R
So the solution inside the barrier is not zero, but it decreases exponentially.
Using the boundary condition it is possible to complete the solution:
\begin{aligned} & \psi_L(x) = C\,e^{ikx} + D\,e^{-ikx} \\ & \psi_R(x) = G\,e^{-\kappa x} \end{aligned}
Continuity of \psi(x) at x=0 gives:
\begin{aligned} & \psi_L(0) = \psi_R(0) \\ & C + D = G \end{aligned}
Continuity of the derivatives \frac{\mathrm d \psi(x)}{\mathrm dx} at x=0 gives:
\begin{aligned} & \frac{\mathrm d \psi_L(0)}{\mathrm dx} = \frac{\mathrm d \psi_R(0)}{\mathrm dx} \\ & ik(C - D) = -\kappa G \\ & C - D = \frac{i\kappa}{k} G \end{aligned}
We can add and subtract these equation to have G as function of C and D:
\begin{aligned} & G = \frac{2k}{k + i\kappa} C \\ & G = \frac{2k}{k - i\kappa} D \end{aligned}
Using these equation it is possible to compute the amplitude of the reflecting wave as function of the incident wave:
D = \frac{k - i\kappa}{k + i\kappa}C
The problem is now solved:
\begin{aligned} & \psi_L(x) = C\,e^{ikx} + D\,e^{-ikx} \\ & D = \frac{k - i\kappa}{k + i\kappa}C \\ & \psi_R(x) = G\,e^{-\kappa x} \\ & G = \frac{2k}{k + i\kappa} C \\ & k = \sqrt{\frac{2mE}{\hbar^2}} \\ & \kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}} \end{aligned}
It is possible to show that the barrier is 100% reflecting:
\left|\frac{C}{D}\right|^2 = \frac{k-i\kappa}{k+i\kappa}\frac{k+i\kappa}{k-i\kappa} = 1
So they have the same magnitude but there is a phase shift.
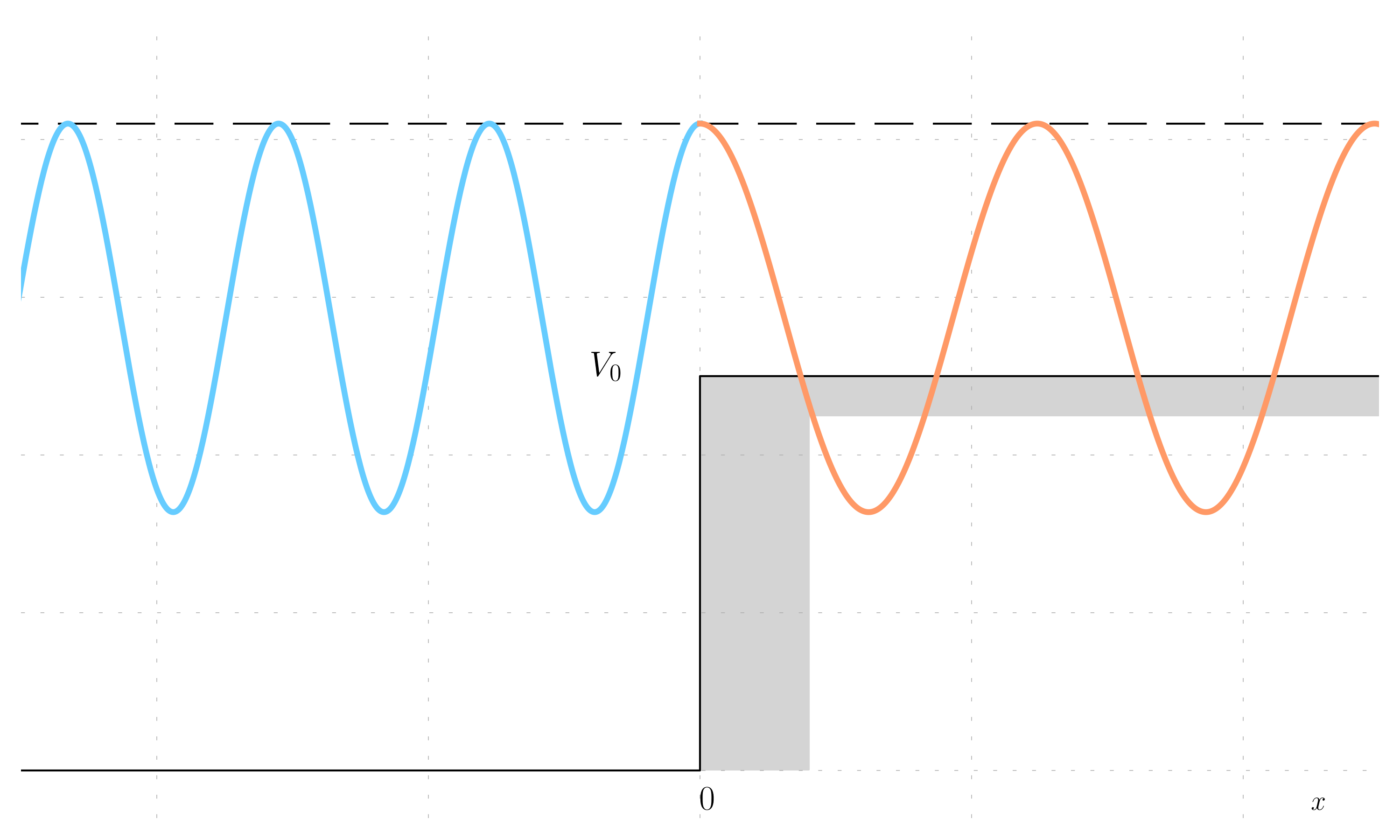
It is possible to plot an example of the real part of a wave hitting a barrier (considering an arbitrary C and an energy which is less that V_0).
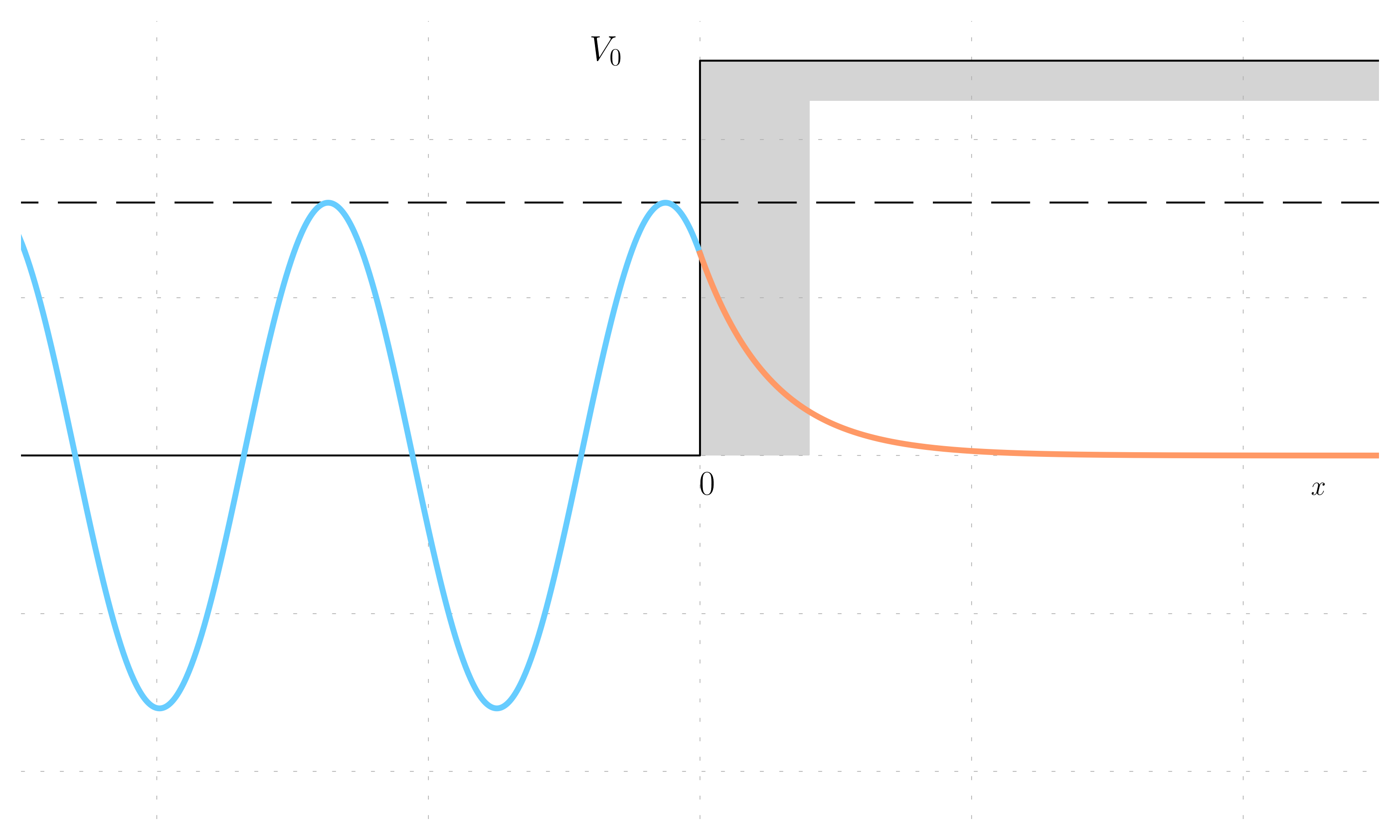
It is possible to make some observations:
- the wave function and its derivative are continuous at x=0, so the two lines have the same value and the same slope;
- there is a phase change on the reflection, the wave does not go to zero nor take the maximum value (which is incidentally |C + D|);
- there is an exponential decay within the barrier, so there is a probability to find the particle within the barrier, which has no analogous in classical mechanics.
Tunneling penetration
The effect of tunnel penetration is well known and understood even for classical wave (it is an important components of for example the transmission over optical fibers), but, since matter is behaving like wave, it is possible to find this penetration with matter too. It is possible to compute some examples to understand the order of magnitude of these.
Considering a barrier of height V_0 = 2\, eV and an electron with an energy of 1\,eV, \kappa is:
\kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}} = \sqrt{\frac{2 \times 9.10938356 \times 10^{-31}\left(2 - 1\right) 1.602176634 \times 10^{-19}}{\left(1.054571817 \times 10^{-34}\right)^2}} \approx 5 \times 10^9 \, m^{-1}
So, the attenuation length (i.e. the length to fall under \frac{1}{e} of the initial value) is:
\frac{1}{\kappa} \approx 0.2 \, nm = 2 \text{\AA}
As the energy increases, the decay gets longer.
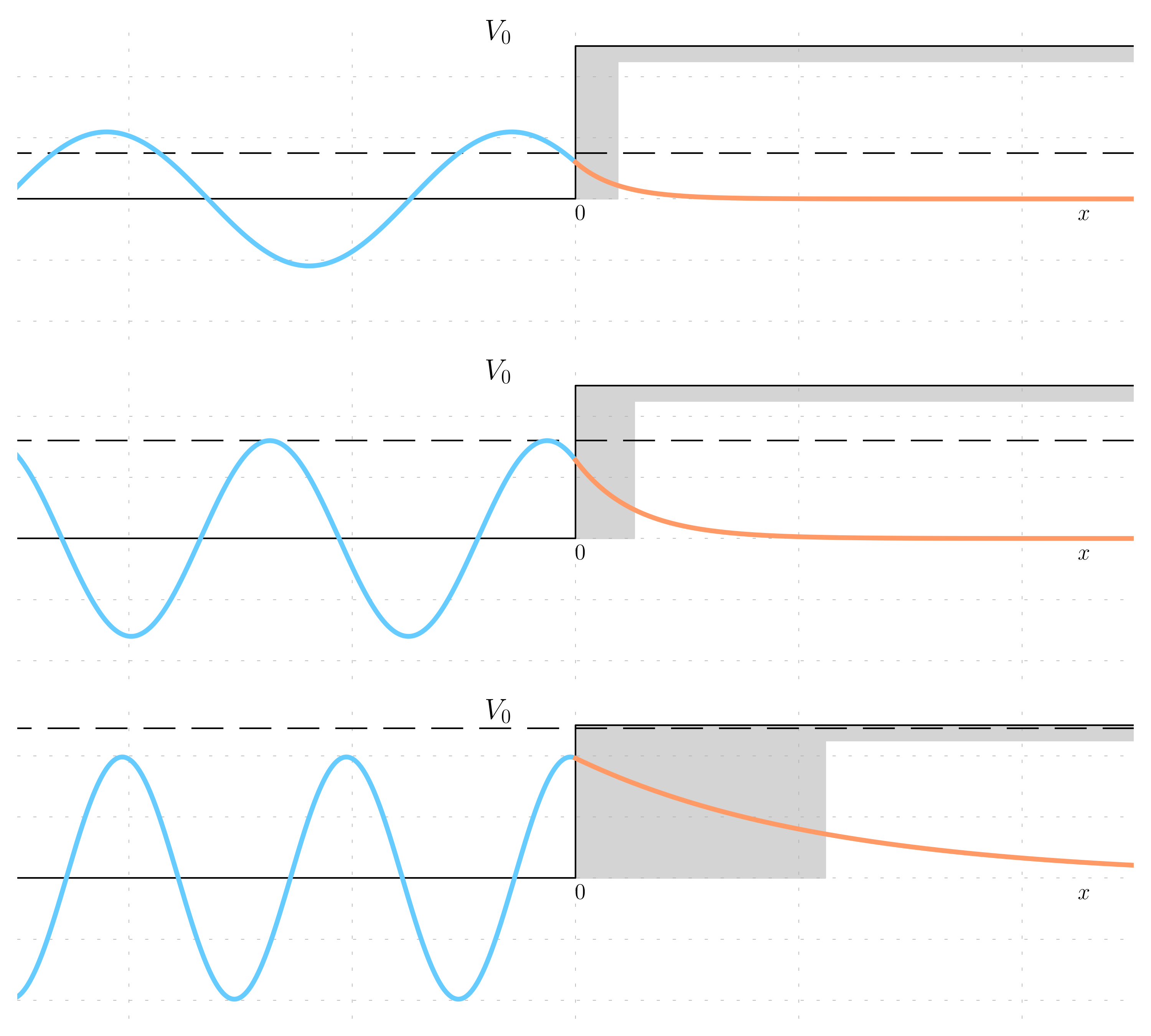
There is also a change in the phase shifts, increasing the energies it is getting close to zero (not exactly zero, but it is noticeable the change).
That was the wave function, which is a complex function; it is more intuitive to look at the probability densities, which are just \propto |\psi(x)|^2.
Since the wave inside the barrier is now \propto e^{-2\kappa x}
On the left there is a standing wave and there are point where the probability density is exactly zero (so the particle will never be found at these points); this happens because there is 100% reflection at the barrier.
Considering the previous example, now the attenuation length is:
\frac{1}{2\,\kappa} \approx 0.1 \, nm = 1 \text{\AA} At lower energy, there phase shift is close to 180^\circ and progressively reduced to being close to zero when the energy is close to V_0.
E > V_0
The Schrödinger equation for x>0 is the same as the one for a free particle in a region where E > V_0:
-\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = (E - V_0)\psi(x)
This rearranges to:
\frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = -\frac{2m(E - V_0)}{\hbar^2}\psi(x)
The general solution is:
\psi_R(x) = F e^{ik_2x} + G e^{-ik_2 x}, \quad k_2 = \sqrt{\frac{2m\left(E-V_0\right)}{\hbar^2}}
As before, the left part is a sum of an incident and a reflected wave, on the right F e^{ik_2x} is the transmitted wave; G e^{-ik_2x} has no physical meaning because there is no way to have a wave reflected from the right towards the origin and therefore G=0:
\psi_R(x) = F e^{ik_2x}, \quad k_2 = \sqrt{\frac{2m\left(E-V_0\right)}{\hbar^2}}
Continuity of \psi(x) at x=0 gives:
\begin{aligned} & \psi_L(0) = \psi_R(0) \\ & C + D = F \end{aligned}
Continuity of the derivatives \frac{\mathrm d \psi(x)}{\mathrm dx} at x=0 gives:
\begin{aligned} & \frac{\mathrm d \psi_L(0)}{\mathrm dx} = \frac{\mathrm d \psi_R(0)}{\mathrm dx} \\ & ik(C - D) = ik_2 F \\ & C - D = \frac{k_2}{k} F \end{aligned}
All quantities can be expressed as a function of C:
\begin{aligned} & D = C\frac{1 - \frac{k_2}{k}}{1 + \frac{k_2}{k}}\\ & F = C\frac{2}{1 + \frac{k_2}{k}} \end{aligned}
The problem is now solved:
\begin{aligned} & \psi_L(x) = C\,e^{ikx} + D\,e^{-ikx} \\ & D = C\frac{1 - \frac{k_2}{k}}{1 + \frac{k_2}{k}}\\ & \psi_R(x) = F\,e^{ik_2 x} \\ & F = C\frac{2}{1 + \frac{k_2}{k}} \\ & k = \sqrt{\frac{2mE}{\hbar^2}} \\ & k_2 = \sqrt{\frac{2m\left(E - V_0\right)}{\hbar^2}} \end{aligned}
The reflection coefficient R and transmission coefficient T can then be calculated to understand the behavior of the wave at the potential step:
\begin{aligned} &R = \left| \frac{D}{C} \right|^2 = \left(\frac{1-\frac{k_2}{k}}{1+\frac{k_2}{k}}\right)^2\\ &T = 1 - R = \frac{k_2}{k}\left| \frac{F}{C} \right|^2 = \frac{4\frac{k_2}{k}}{\left(1+\frac{k_2}{k}\right)^2} \end{aligned}
The solution is shown below:
This solution is an example of scattering.
Finite tick barrier
Considering a potential V(x) such as:
V(x) = \begin{cases} 0 & \quad x \le 0 \\ V_0 & \quad 0 < x < L \\ 0 & \quad x \ge L \end{cases}
On the left, the solution is described in the same way as the infinitely tick case with a waves as:
\psi_L(x) = C\,e^{ikx} + D\,e^{-ikx}, \quad k = \sqrt{\frac{2mE}{\hbar^2}}
C\,e^{ikx} is incident wave (going to the right) and D\,e^{-ikx} is the reflected wave (going to the left).
E < V_0
Inside the barrier (0 < x < L), the Schrödinger equation hold (with V_0 - E > 0):
\begin{aligned} & -\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} + V_0\psi(x) = E\psi(x) \\ & \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = \frac{2m}{\hbar^2} \left( V_0 - E \right)\psi(x) \end{aligned}
The solution of this equation can be written as:
\psi_B(x) = F\,e^{\kappa x} + G\,e^{-\kappa x}, \quad \kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}}, \quad \kappa \in \mathbb R
The Schrödinger equation for x>L is the same as the one for a free particle:
\psi_R(x) = H\,e^{ikx} + I\,e^{-ikx}, \quad k = \sqrt{\frac{2mE}{\hbar^2}}
For a similar consideration as the infinite case, for x >L there is no a wave reflected from the right towards the origin and therefore I=0:
\psi_R(x) = H\,e^{ikx}, \quad k = \sqrt{\frac{2mE}{\hbar^2}}
It is now possible to apply the boundary conditions; the continuity of \psi(x) at x=0 and x=L gives:
\begin{aligned} & \psi_L(0) = \psi_B(0) \\ & C + D = F + G \\ & \psi_B(L) = \psi_R(L) \\ & F e^{\kappa L} + G e^{-\kappa L} = H e^{ikL} \end{aligned}
Continuity of the derivatives \frac{\mathrm d \psi(x)}{\mathrm dx} at x=0 gives:
\begin{aligned} & \frac{\mathrm d \psi_L(0)}{\mathrm dx} = \frac{\mathrm d \psi_B(0)}{\mathrm dx} \\ & ik(C - D) = \kappa (F-G) \\ & \frac{\mathrm d \psi_B(L)}{\mathrm dx} = \frac{\mathrm d \psi_R(L)}{\mathrm dx} \\ & \kappa\left(F e^{\kappa L} - G e^{-\kappa L}\right) = ik He^{ikL} \end{aligned}
The results are four equations in five unknown:
\begin{aligned} & C + D = F + G \\ & F e^{\kappa L} + G e^{-\kappa L} = H e^{ikL} \\ & ik(C - D) = \kappa (F-G) \\ & \kappa\left(F e^{\kappa L} - G e^{-\kappa L}\right) = ik He^{ikL} \end{aligned}
These can be solved as function of C.
Multiplying the first equation by ik and using the third:
\begin{aligned} & ik(C + D) = ik(F + G) \\ & ik(C + D) + ik(C - D) = ik(F + G) + \kappa (F-G) \\ & 2ikC = F (ik + \kappa) +G (ik - \kappa) \\ & ik(C + D) - ik(C - D) = ik(F + G) - \kappa (F-G) \\ & 2ikD = F (ik - \kappa) + G (ik + \kappa) \end{aligned}
` Multiplying the second equation by \kappa and using the fourth:
\begin{aligned} & \kappa\left(F e^{\kappa L} + G e^{-\kappa L}\right) = \kappa H e^{ikL} \\ & \kappa\left(F e^{\kappa L} + G e^{-\kappa L}\right) + \kappa\left(F e^{\kappa L} - G e^{-\kappa L}\right) = \kappa H e^{ikL} + ik He^{ikL} \\ & 2\kappa F e^{\kappa L} = \left(\kappa H + ik\right) e^{ikL} \\ & \kappa\left(F e^{\kappa L} + G e^{-\kappa L}\right) - \kappa\left(F e^{\kappa L} - G e^{-\kappa L}\right) = \kappa H e^{ikL} - ik He^{ikL} \\ & 2\kappa G e^{-\kappa L} = \left(\kappa H - ik\right) e^{ikL} \end{aligned}
Now it is necessary to manipulate these 4 equations:
\begin{aligned} & 2ikC = F (ik + \kappa) +G (ik - \kappa) \\ & 2ikD = F (ik - \kappa) + G (ik + \kappa) \\ & 2\kappa F e^{\kappa L} = \left(\kappa H + ik\right) e^{ikL} \\ & 2\kappa G e^{-\kappa L} = \left(\kappa H - ik\right) e^{ikL} \end{aligned}
These can be solved and the correspondent parameters computed.
\begin{aligned} D &= \frac{ (k-i \kappa ) (k+i \kappa ) \left(e^{2 \kappa L}-1\right)}{\kappa ^2+k^2 e^{2 \kappa L}-k^2+2 i \kappa k+2 i \kappa k e^{2 \kappa L}-\kappa ^2 e^{2 \kappa L}}C \\ F &= -\frac{2 k (k-i \kappa )}{\kappa ^2+k^2 e^{2 \kappa L}-k^2+2 i \kappa k+2 i \kappa k e^{2 \kappa L}-\kappa ^2 e^{2 \kappa L}} C \\ G &= \frac{2 k (k+i \kappa ) e^{2 \kappa L}}{\kappa ^2+k^2 e^{2 \kappa L}-k^2+2 i \kappa k+2 i \kappa k e^{2 \kappa L}-\kappa ^2 e^{2 \kappa L}}C \\ H &= -\frac{\kappa k e^{\kappa L-i k L}}{i \kappa ^2+i k^2 e^{2 \kappa L}-i k^2-2 \kappa k-2 \kappa k e^{2 \kappa L}-i \kappa ^2 e^{2 \kappa L}}C \end{aligned}
The solution is shown below:
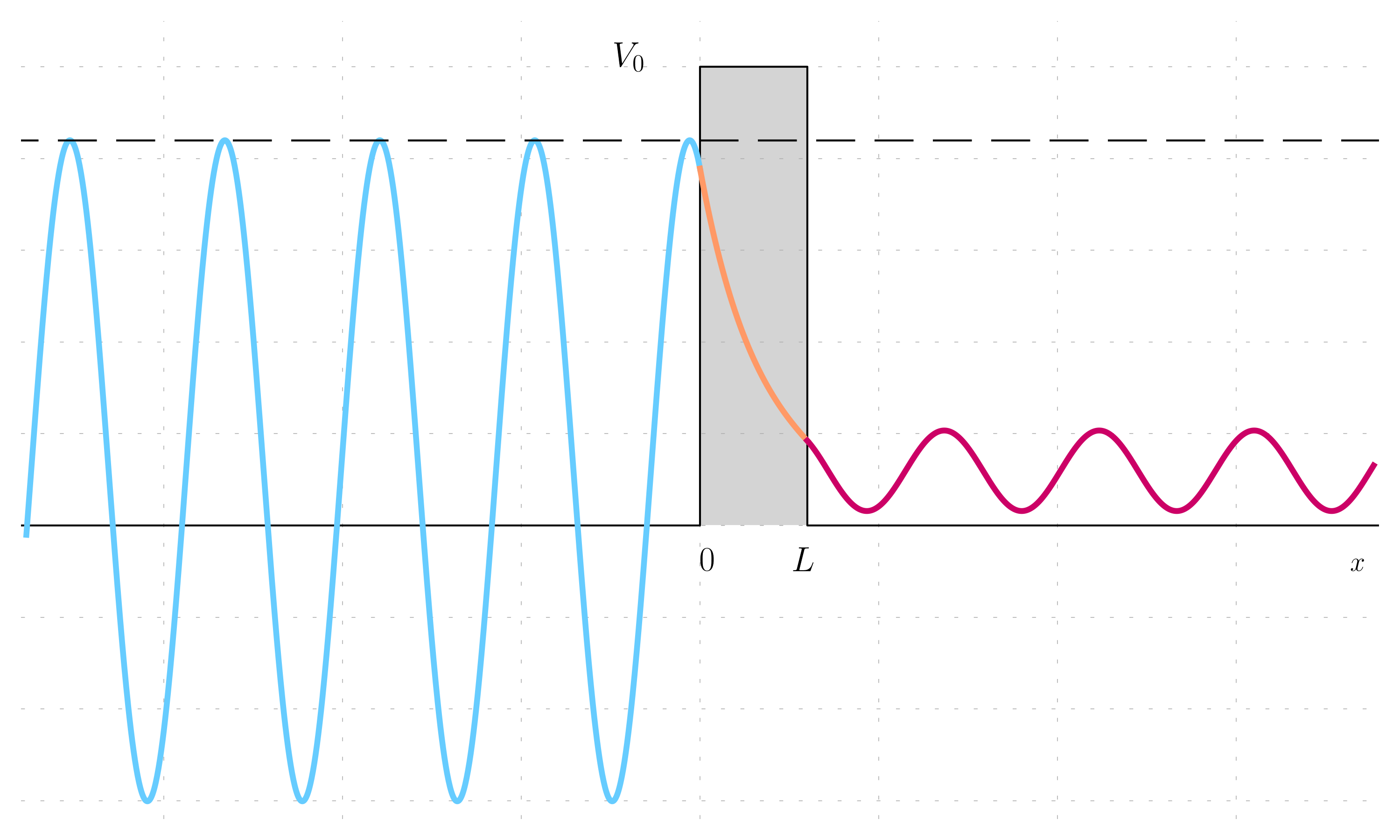
The wavelength is the same on both sides of the barrier, but the amplitude beyond the barrier is less than the original amplitude. The particle can never be found inside the barrier, but it can be observed beyond the barrier; this is the quantum tunnelling effect described previously for the infinite barrier.
E > V_0
The Schrödinger equation above the barrier the same as the one for a free particle in a region where E > V_0:
-\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = (E - V_0)\psi(x)
This rearranges to:
\frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = -\frac{2m(E - V_0)}{\hbar^2}\psi(x)
The general solution is:
\psi_R(x) = F e^{ik_2x} + G e^{-ik_2 x}, \quad k_2 = \sqrt{\frac{2m\left(E-V_0\right)}{\hbar^2}}
The Schrödinger equation for x>L is the same as the one for a free particle:
\psi_R(x) = H\,e^{ikx} + I\,e^{-ikx}, \quad k = \sqrt{\frac{2mE}{\hbar^2}}
For a similar consideration as the infinite case, for x >L there is no a wave reflected from the right towards the origin and therefore I=0:
\psi_R(x) = H\,e^{ikx}, \quad k = \sqrt{\frac{2mE}{\hbar^2}}
It is now possible to apply the boundary conditions; the continuity of \psi(x) at x=0 and x=L gives:
\begin{aligned} & \psi_L(0) = \psi_B(0) \\ & C + D = F + G \\ & \psi_B(L) = \psi_R(L) \\ & F e^{i k_2 L} + G e^{-i k_2 L} = H e^{ikL} \end{aligned}
Continuity of the derivatives \frac{\mathrm d \psi(x)}{\mathrm dx} at x=0 gives:
\begin{aligned} & \frac{\mathrm d \psi_L(0)}{\mathrm dx} = \frac{\mathrm d \psi_B(0)}{\mathrm dx} \\ & k(C - D) = k_2 (F-G) \\ & \frac{\mathrm d \psi_B(L)}{\mathrm dx} = \frac{\mathrm d \psi_R(L)}{\mathrm dx} \\ & k_2\left(F e^{i k_2 L} - G e^{-i k_2 L}\right) = k He^{ikL} \end{aligned}
The results are four equations in five unknown:
\begin{aligned} & C + D = F + G \\ & F e^{i k_2 L} + G e^{-i k_2 L} = H e^{ikL} \\ & k(C - D) = k_2 (F-G) \\ & k_2\left(F e^{i k_2 L} - G e^{-i k_2 L}\right) = k He^{ikL} \end{aligned}
These can be solved as function of C.
Multiplying the first equation by k and using the third:
\begin{aligned} & k(C + D) = k(F + G) \\ & k(C + D) + k(C - D) = k(F + G) + k_2 (F-G) \\ & 2kC = F (k + k_2) + G (k - k_2) \\ & k(C + D) - k(C - D) = k(F + G) - k_2 (F-G) \\ & 2kD = F (k - k_2) + G (k + k_2) \end{aligned}
` Multiplying the second equation by k_2 and using the fourth:
\begin{aligned} & k_2 \left(F e^{i k_2 L} + G e^{-i k_2 L}\right) = k_2 H e^{ikL} \\ & k_2 \left(F e^{i k_2 L} + G e^{-i k_2 L}\right) + k_2\left(F e^{i k_2 L} - G e^{-i k_2 L}\right) = \left(k_2 + k\right) H e^{ikL} \\ & 2k_2 F e^{i k_2 L} = \left(k_2 + k\right) H e^{ikL}\\ & k_2\left(F e^{i k_2 L} + G e^{-i k_2 L}\right) - k_2\left(F e^{i k_2 L} - G e^{-i k_2 L}\right) = k_2 H e^{ikL} - k He^{ikL} \\ & 2k_2 G e^{-i k_2 L} = \left(k_2 - k\right) H e^{ikL} \end{aligned}
Now it is necessary to manipulate these 4 equations:
\begin{aligned} & 2kC = F (k + k_2) + G (k - k_2) \\ & 2kD = F (k - k_2) + G (k + k_2) \\ & 2k_2 F e^{i k_2 L} = \left(k_2 + k\right) H e^{ikL} \\ & 2k_2 G e^{-i k_2 L} = \left(k_2 - k\right) H e^{ikL} \end{aligned}
These can be solved and the correspondent parameters computed.
\begin{aligned} D &= \frac{(k-k_2) (k+k_2) \left(-1+e^{2 i k_2 L}\right)}{k^2 e^{2 i k_2 L}-k^2-2 k k_2 e^{2 i k_2 L}-2 k k_2+k_2^2 e^{2 i k_2 L}-k_2^2} C\\ F &= -\frac{2 k (k+k_2)}{k^2 e^{2 i k_2 L}-k^2-2 k k_2 e^{2 i k_2 L}-2 k k_2+k_2^2 e^{2 i k_2 L}-k_2^2}C \\ G &= \frac{2 k (k-k_2) e^{2 i k_2 L}}{k^2 e^{2 i k_2 L}-k^2-2 k k_2 e^{2 i k_2 L}-2 k k_2+k_2^2 e^{2 i k_2 L}-k_2^2}C \\ H &= -\frac{4 k k_2 e^{i k_2 L-i k L}}{k^2 e^{2 i k_2 L}-k^2-2 k k_2 e^{2 i k_2 L}-2 k k_2+k_2^2 e^{2 i k_2 L}-k_2^2}C \end{aligned}
The solution is shown below:
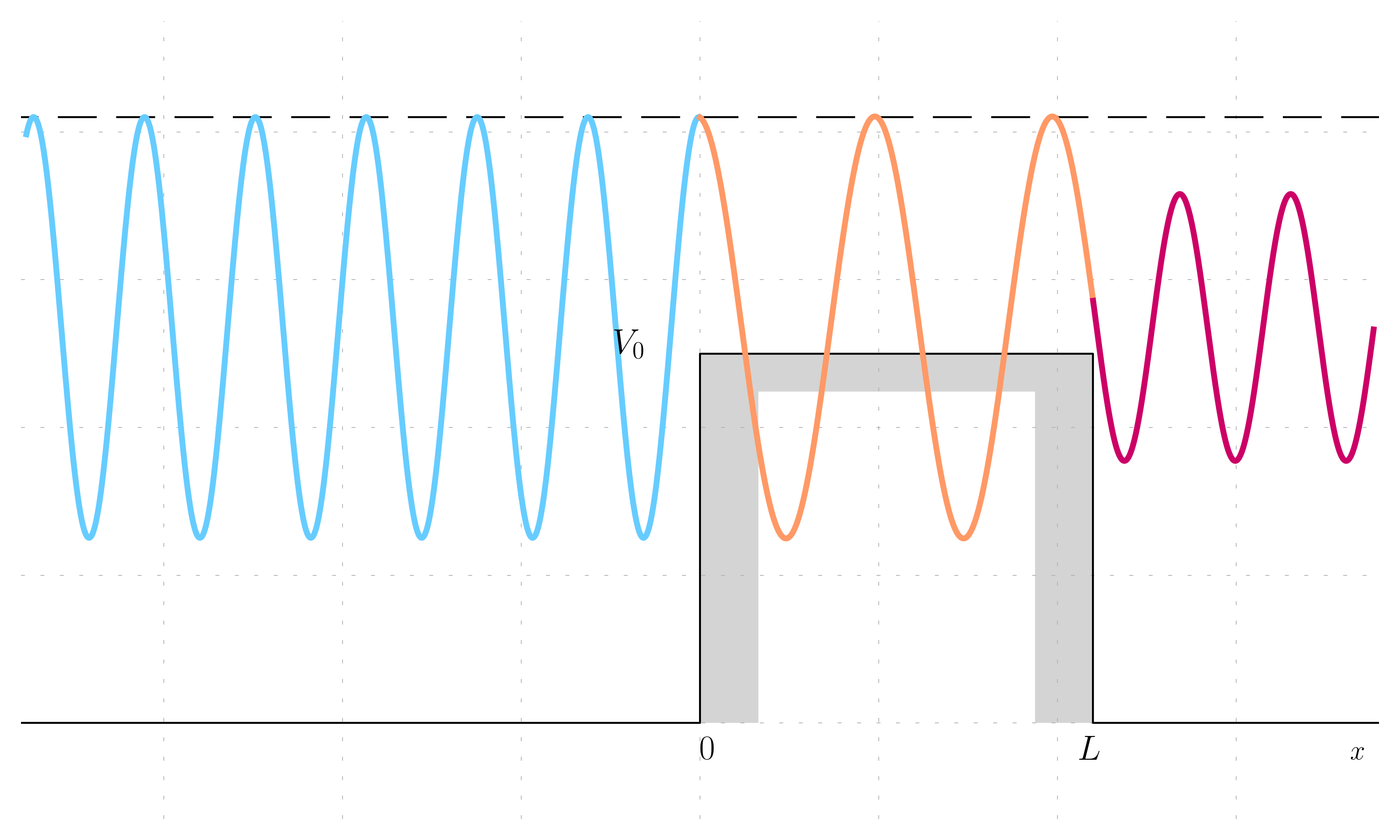
In classical mechanics, when a particle encounters a potential barrier with energy greater than the barrier height (E > V_0), it proceeds undisturbed, its trajectory and energy unaffected by the barrier. In contrast, there is a different outcome here: the presence of the potential barrier affects the particle’s wave function, leading to a change in amplitude due to the potential change. This modulation of amplitude reflects the quantum nature of particles, emphasizing that unlike in classical physics, the characteristics of the wave function are in general influenced by variations in potential.
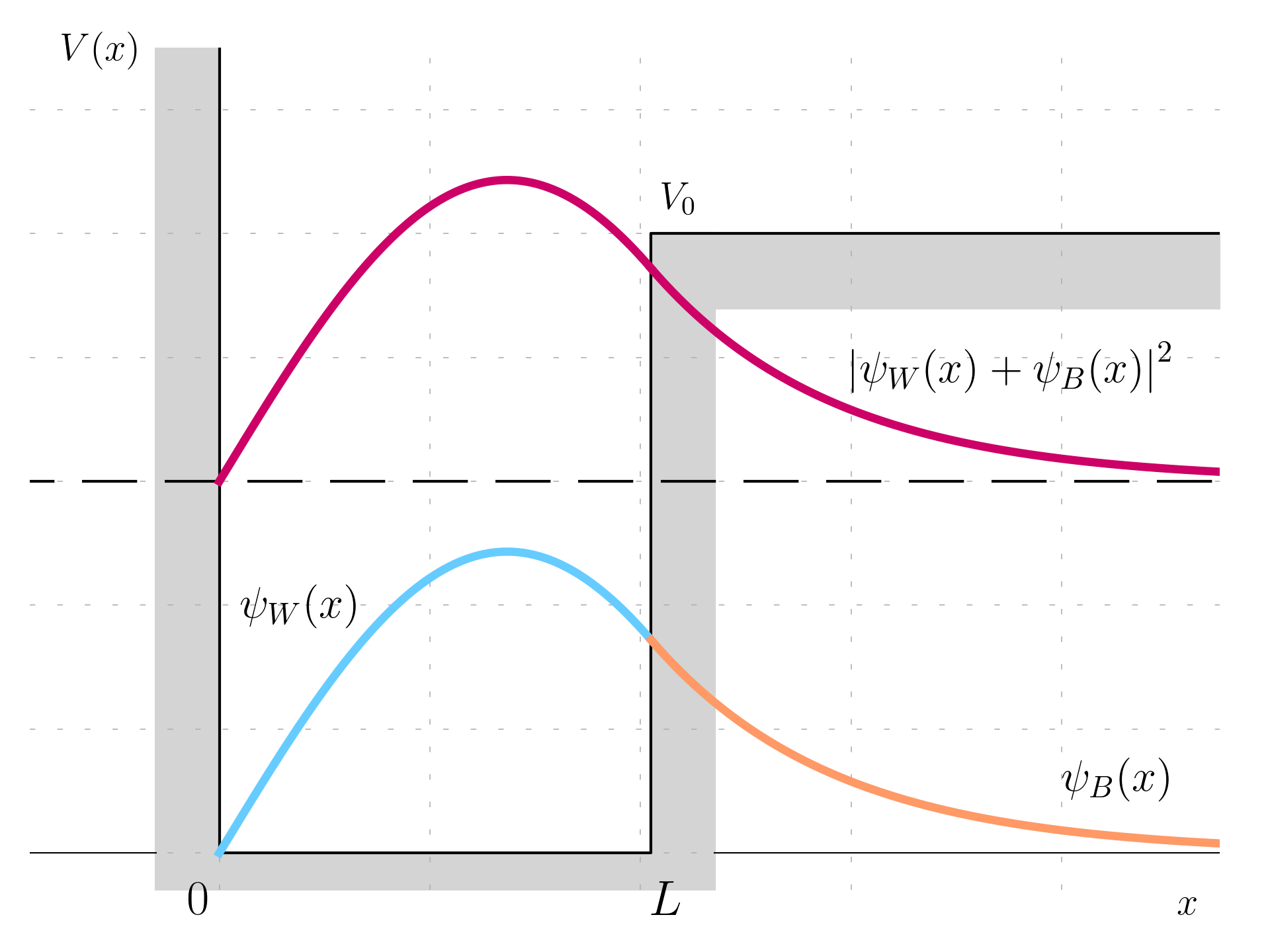
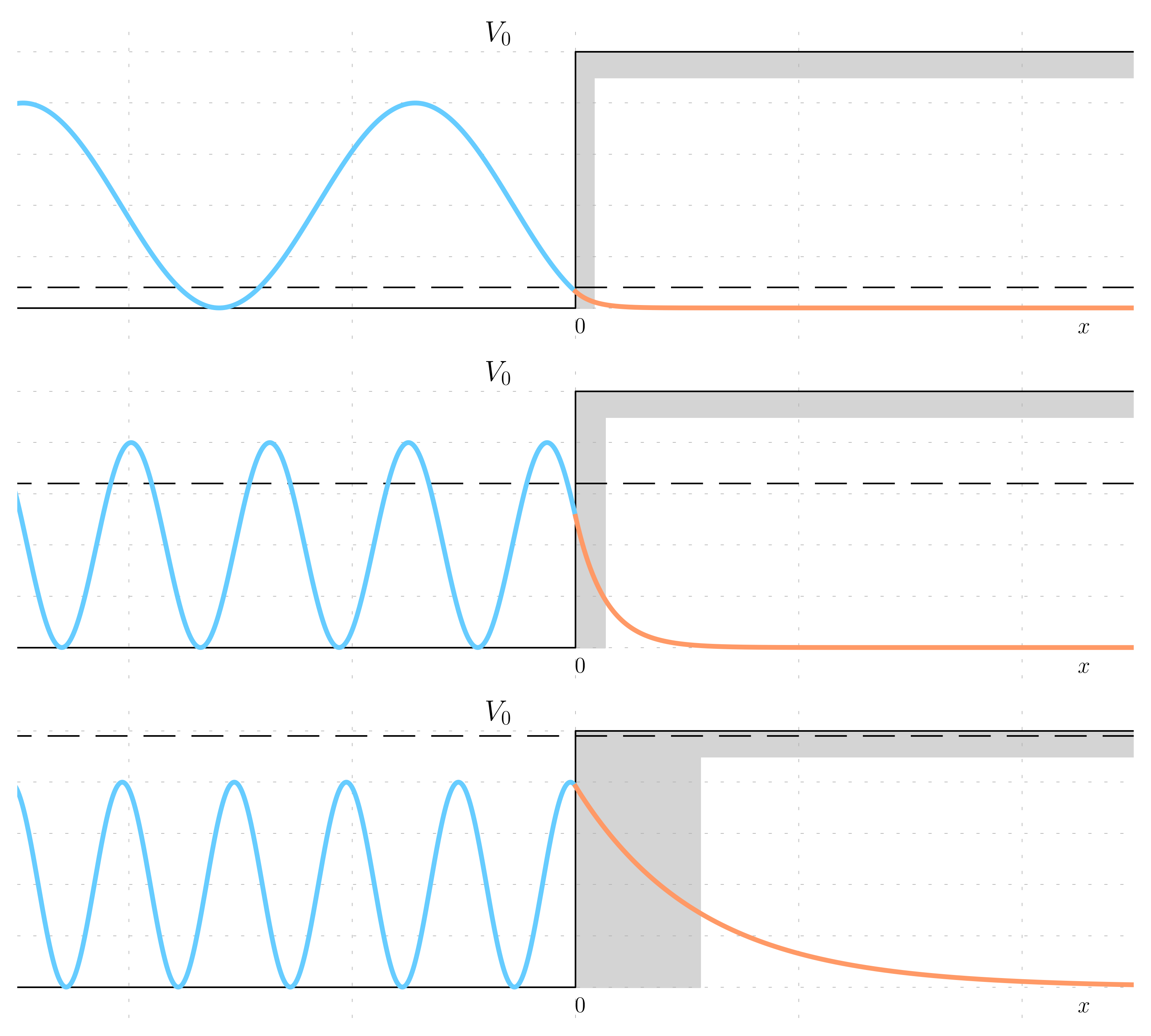
Well with Infinite Tick Barrier
Considering a potential V(x) such as:
V(x) = \begin{cases} \infty & \quad x \le 0 \\ 0 & \quad 0 \le x \le L \\ V_0 & \quad x \ge L \end{cases}
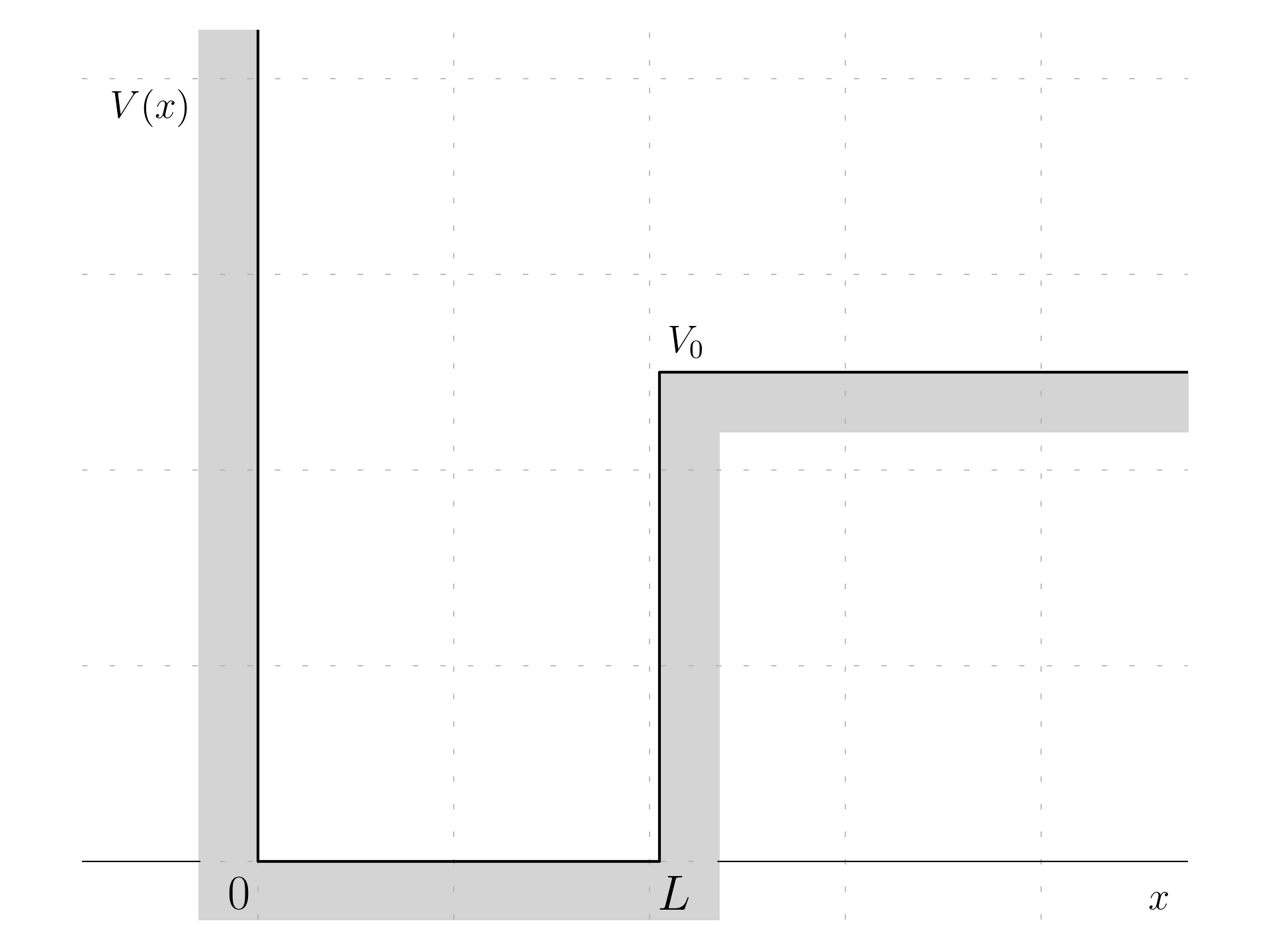
Let’s suppose that the thickness L is such as that the lowest eigenenergy is such as:
E_1 = \frac{V_0}{2}
Within the well, the potential V(x) =0 and the Schrödinger equation is:
-\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = E\psi(x)
The solution of this equation is:
\psi_W(x) = A\,\sin(kx) + B\,\cos(kx)
Since the barrier is infinitely high on the left, the boundary condition is:
\psi_W (0) = 0
Which implies:
\psi_W(0) = A\,\sin(0) + B\,\cos(0) = B = 0
so the solution is:
\psi_W = A\sin(kx)
Using the Schrödinger equation gives:
k = \sqrt{\frac{2Em}{\hbar}}
So the solution is:
\psi_W = A\sin(kx), \quad k = \sqrt{\frac{2Em}{\hbar}}
within the barrier, the potential is Inside the barrier, the Schrödinger equation hold (with V_0 - E > 0) is:
\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = \left( V_0 - E\right)\psi(x)
and the solution can be written as:
\psi_B(x) = C\,e^{\kappa (x-L)} + D\,e^{-\kappa (x-L)}
D=0 because otherwise the wave function will be growing exponentially and it won’t be possible to normalize the solution. So the solution will be:
\psi_B(x) = C\,e^{-\kappa (x-L)}
Using the Schrödinger equation gives:
\kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}}
So the solution is
\psi_B(x) = C\,e^{-\kappa (x-L)}, \quad \kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}}
Considering a case for which E_1 = \frac{V_0}{2}, in the well:
k = \sqrt{\frac{2E_1m}{\hbar}}
In the barrier:
\kappa = \sqrt{\frac{2m\left(V_0 - E_1\right)}{\hbar^2}} = \sqrt{\frac{2m\left(2E_1 - E_1\right)}{\hbar^2}} = \sqrt{\frac{2mE_1}{\hbar^2}} = k
So:
\psi_B(x) = C\,e^{-k (x-L)}
It is possible to apply the continuity of the wave function and its derivatives for x = L to compute the coefficients:
\begin{aligned} & \psi_W(L) = A\,\sin(kL) \\ & \psi_B(L) = C \\ & \frac{\mathrm d\psi_W(L)}{\mathrm dx} = kA\,\cos(kL) \\ & \frac{\mathrm d\psi_B(L)}{\mathrm dx} =-kC \\ \end{aligned}
Combining these equations:
\begin{aligned} & A\,\sin(kL) = C \\ & A\,\cos(kL) = -C \\ & \tan(kL) = -1 \\ & kL = \frac{3}{4}\pi \\ & C = A\,\sin(kL) = A\frac{\sqrt 2}{2} \end{aligned}
The solution is therefore:
\psi(x) = \psi_W(x) + \psi_B(x) = A\left[\sin(kx) + \frac{\sqrt 2}{2}e^{-k (x-L)}\right]
To compute the full solution is necessary to normalize the wavefunction, since \psi_W is zero within the barrier and vice-versa, the normalization condition is:
\begin{aligned} & A^2\left[\int_0^L \sin^2(kx) \, \mathrm dx + \int_L^\infty \frac{1}{2}e^{-2k (x-L)}\, \mathrm dx \right] = 1 \\ & A^2\left\{ \left[ \frac{L}{2} - \frac{\sin(2kL)}{4k}\right] + \left[ \frac{1}{4k} \right] \right\} = 1 \\ \end{aligned}
Using kL = \frac{3}{4}\pi:
\begin{aligned} & A^2 \left[ \frac{L}{2} - \frac{\sin\left(\frac{3}{2}\pi\right)}{4k} + \frac{1}{2k} \right] = A^2\left( \frac{L}{2} + \frac{1}{4k} + \frac{1}{4k} \right) = A^2\left( \frac{L}{2} + \frac{1}{2k} \right) = 1 \end{aligned}
Defining F = \frac{A}{\sqrt{L}} and substituting:
\begin{aligned} & \frac{F^2}{L}\left( \frac{L}{2} + \frac{1}{2k} \right) = \frac{F^2}{2} \left(1 + \frac{1}{kL}\right) = \frac{F^2}{2}\left(1 + \frac{4}{3\pi}\right) = 1 \\ & F = \sqrt{\frac{2}{1 + \frac{4}{3\pi}}} \approx 1.185 \end{aligned}
It is the possible to plot the wavefunction and the probability density for this problem.