Tunneling Probabilities
Considering a rectangular barrier of height V_0. This problem has been analyzed here
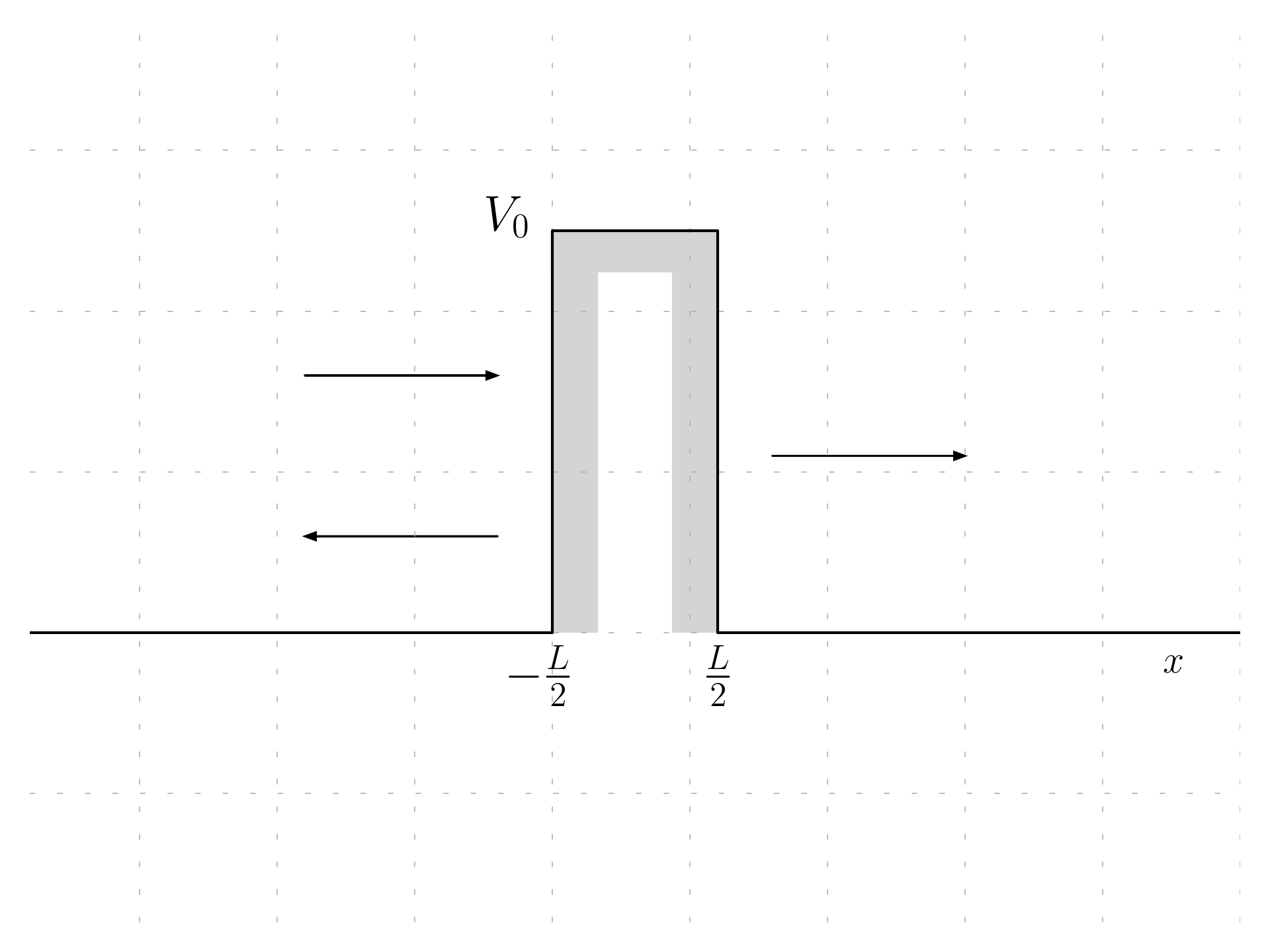
Let’s suppose there are some incident electrons with energy E < V_0, so the solution on the left is a forward and backward propagating wave, and on the right there is just a propagating wave:
\begin{aligned} & \psi_L = Ae^{ikx} + B e^{-ikx} \\ & \psi_R = Fe^{ik_Rx} \end{aligned} and the coefficient might differ if the potential left and right aren’t the same. The solution within the barrier will be a decaying exponential:
\psi_B = C e^{-\kappa x} + De^{\kappa x}
As a result, the relation between these constant is now known.
To relate these to current, we start from the definition of the particle current density in quantum mechanics:
\mathbf j_p = \frac{i\hbar}{2m}\left(\Psi \nabla \bar \Psi - \bar \Psi \nabla \Psi\right)
This function is time dependent but if we assume to deal with particles with a defined energy E, then:
\Psi(\mathbf r,t) = \psi(\mathbf r) e^{-i\frac{E}{\hbar}t}
and the time dependent factor cancel out and it reduces to:
\mathbf j_p = \frac{i\hbar}{2m}\left(\psi \nabla \bar \psi - \bar \psi \nabla \psi\right)
In the one dimensional case, it is necessary to compute only the x component and for a simple barrier with the same potential on the left and the right, the left side is:
j_p = \frac{i\hbar}{2m}\left[ \left(Ae^{ikx} + B e^{-ikx}\right)\frac{\mathrm d}{\mathrm dx}\left(\bar A e^{-ikx} + \bar B e^{ikx}\right) - \left(\bar Ae^{-ikx} + \bar B e^{ikx}\right)\frac{\mathrm d}{\mathrm dx} \left(Ae^{ikx} + B e^{-ikx}\right)\right] = \left(|A|^2 - |B|^2\right)\frac{\hbar k}{m}
and the right side:
j_p = \frac{i\hbar}{2m}\left(Fe^{ikx} \frac{\mathrm d}{\mathrm dx}\bar Fe^{-ikx} - \bar Fe^{-ikx} \frac{\mathrm d}{\mathrm dx} Fe^{ikx}\right) = |F|^2\frac{\hbar k}{m}
There is an interesting point to note: the current on the left does not vary with the space, which is surprising as the probability density does vary with the space.
The fraction transmitted by the barrier can be written as:
\eta = \frac{|A|^2 - |B|^2}{|A|^2} = \frac{|F|^2}{|A|^2}
The last equality is valid only for the case where the potential on the left and the potential on the right have the same value, while the first one is always valid.
For example, considering the case where the potential are not the same, we would have a different constant k on each side and therefore:
\begin{aligned} & j_p = \left(|A|^2 - |B|^2\right)\frac{\hbar k_L}{m} \\ & j_p = |F|^2\frac{\hbar k_R}{m} \\ & \left(|A|^2 - |B|^2\right)\frac{\hbar k_L}{m} = |F|^2\frac{\hbar k_R}{m} \\ & \eta = \frac{|A|^2 - |B|^2}{|A|^2} = \frac{k_R}{k_L}\frac{|F|^2}{|A|^2} \end{aligned}