Tight Binding Model
The tight binding method is a semi-empirical approach used in quantum mechanics to describe the electronic structure of solid materials, particularly in the field of condensed matter physics. The rationale behind using this method lies in its ability to provide a reasonable approximation of the electronic behavior while maintaining computational efficiency, making it suitable for studying large systems that would be challenging to handle with more computationally expensive methods.
The tight binding method is based on the idea that in a solid, the electrons are tightly bound to their respective atoms, and their wavefunctions can be approximated as a linear combination of atomic orbitals. This approximation is particularly useful when studying materials with strong localization of electrons, such as semiconductors and insulators, where the electrons are tightly bound to the atomic nuclei.
The tight binding method can be useful in the following situations:
-
Studying the electronic band structure of solids: The method can provide insight into the energy levels and dispersion relations of electrons in crystalline solids, which is crucial for understanding their electrical, optical, and transport properties.
-
Modeling defects and impurities: The tight binding method can be employed to investigate the effects of defects, such as vacancies, interstitials, and impurities, on the electronic structure of materials.
-
Simulating quantum transport: The tight binding approach can be used to model the transport of electrons in nanoscale devices, such as quantum wires and quantum dots, where quantum effects become significant.
-
Exploring low-dimensional systems: The tight binding method is particularly suitable for studying the electronic properties of low-dimensional systems, such as graphene, carbon nanotubes, and topological insulators, where the effects of dimensionality play a crucial role.
The tight binding method is considered a decent approximation for simulating reality because it strikes a balance between accuracy and computational efficiency. While it may not provide the same level of precision as more sophisticated methods, it can capture the essential physics of the system and provide qualitative insights into the electronic structure.
However, it is important to note that the accuracy of the tight binding method depends on the choice of parameters used to describe the atomic orbitals and their interactions. These parameters are often derived from experimental data or more accurate calculations, introducing some empirical elements into the method.
Overall, the tight binding method is a valuable tool in the field of quantum mechanics, particularly when studying the electronic properties of solid-state systems, as it offers a computationally efficient way to gain insights into the behavior of electrons in materials while providing a reasonable approximation of reality.
Coupled finite wells
Let’s consider two finite potential wells, which are separated by some distance (the energy origin will be chosen at the top).
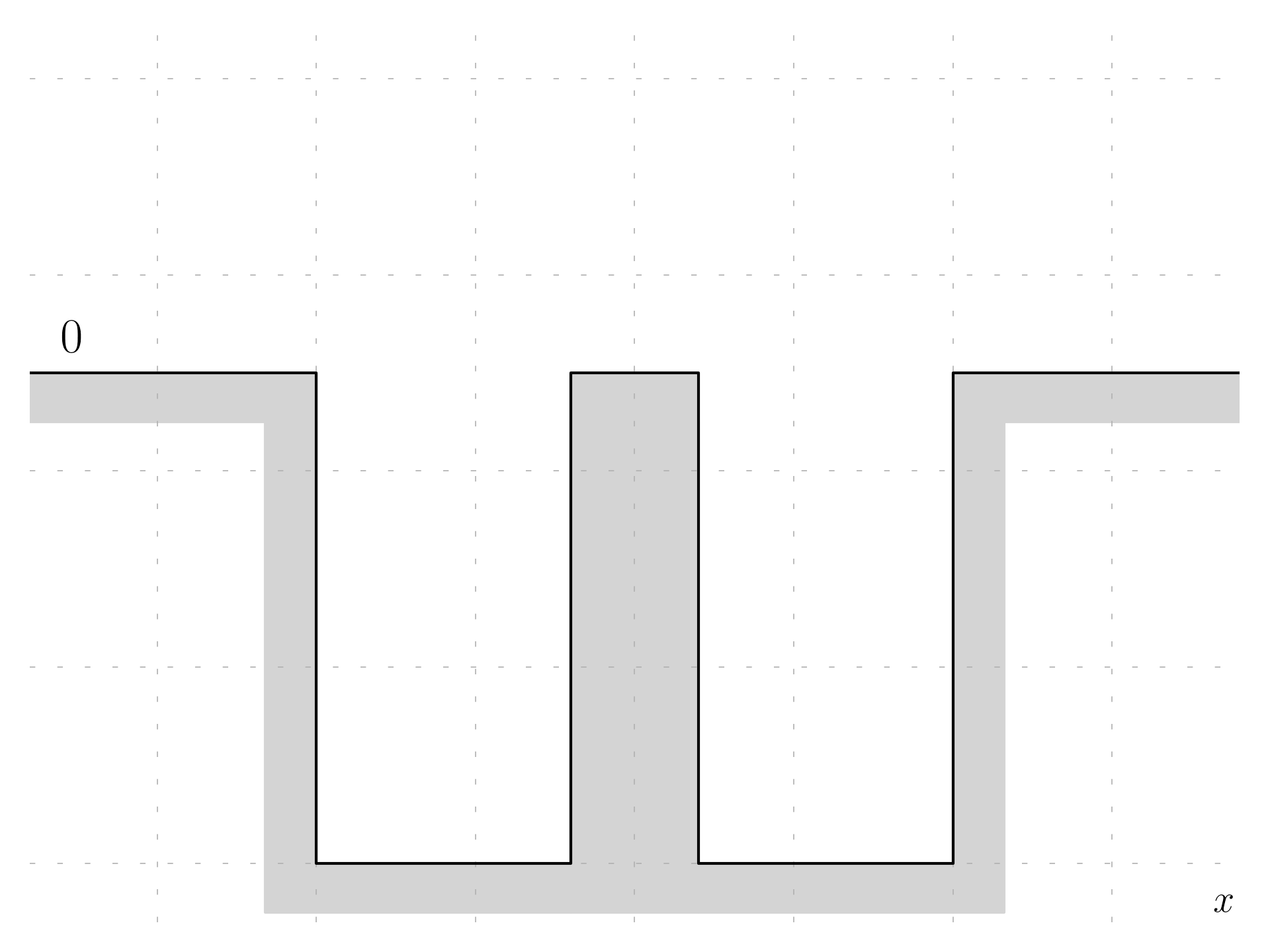
The first step is to consider two separated unperturbed potential wells. This is a problem that can be solved (an example here).
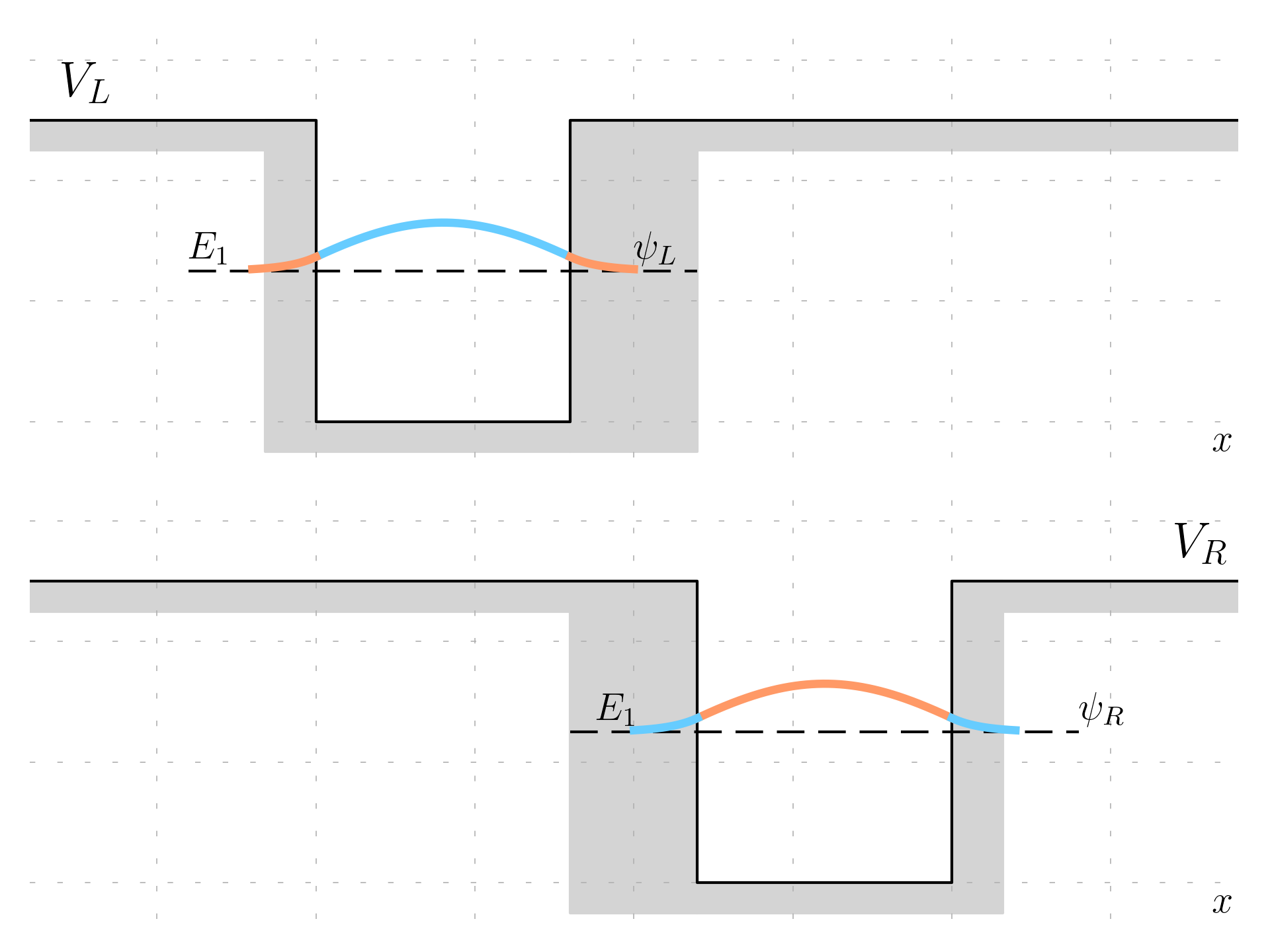
These wells will have a potential V_L and V_R and a solution (for example considering the first state, E_1 and \psi_L(x) and \psi_r(x) as wavefunctions).
The entire potential will be a function V(x) which has the shape with two wells; since the origin has been chosen at the top of the well, it is possible to say that the coupled potential is the sum of the two potential wells:
V(x) = V_L + V_R
The Hamiltonian for this system is therefore:
\mathbf H = -\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R
The approximation methods consists in taking a finite basis set which is composed just from the two eigenfunctions \psi_L and \psi_R; a further assumption is to consider that these two functions are orthogonal (and that is a good approximation if the barrier in between is reasonably thick).
That is the basis of the approximation model, the wavefunctions are assumed to be tightly confined in the respective well.
If these are effectively the basis function for the solution, the total wavefunction can be written as:
\psi \approx \alpha \psi_L + \beta \psi_R
With the above formulation, it is possible to apply the same matrix scheme as in the finite matrices approximation method:
\begin{bmatrix} H_{11} & H_{12} \\ H_{21} & H_{22} \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = E\begin{bmatrix} \alpha \\ \beta \end{bmatrix}
Then it is a matter of plug the coefficient above:
H_{11} = \int_{-\infty}^\infty \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R\right)\psi_L \mathrm dx
So the approximation made is that in the right well \psi_L = 0, so \bar\psi_L V_R \psi_L \approx 0 and:
H_{11} = \int_{-\infty}^\infty \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L\right)\psi_L \mathrm dx = E_1
Similarly, \bar \psi_R V_L \psi_R \approx 0 and therefore:
H_{22} = \int_{-\infty}^\infty \bar \psi_R \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_R\right)\psi_R \mathrm dx = E_1
For the off diagonal terms there are few contributions (starting from H_{12}):
\begin{aligned} H_{12} = & \int_{-\infty}^\infty \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R\right)\psi_R \mathrm dx \\ = & \int_{-\infty}^{\text{L}} \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R\right)\psi_R \mathrm dx + \int_{\text{barrier}} \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R \right)\psi_R \mathrm dx \\& + \int_{\text{R}}^{-\infty} \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R\right)\psi_R \mathrm dx = I_1 + I_2 + I_3 \end{aligned}
Of these three integral:
- I_1 = 0 because \psi_R = 0 in the domain of interest;
- I_3 = 0 because \bar \psi_L = 0 in the domain of interest;
- for I_2 V_L and V_R are zero within the barrier.
So the only contribution left is:
H_{12} = \int_{\text{barrier}} \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2}\right)\psi_R \mathrm dx = \Delta E
This integral is not zero because the wavefunction have a small contribution within the barrier.
This integral can be analytically solved, assuming the x origin to be the left wall of the left well, so the integral goes from L, the length of the well, to L + L_b, with L_b the length of the barrier, and the functions are from here:
\begin{aligned} \Delta E = & \int_{\text{barrier}} \bar \psi_L \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2}\right)\psi_R \mathrm dx = \int_L^{L+L_b}F e^{-\kappa \left(x-\frac{L}{2}\right)} \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2}\right)G e^{\kappa \left(x-\frac{L}{2}- L_b\right)}\mathrm dx \\ & =-\frac{F^2\hbar^2}{2m} \int_L^{L+L_b}e^{-\kappa \left(x-\frac{L}{2}\right)} \left(\frac{\mathrm d^2}{\mathrm dx^2}\right) e^{\kappa \left(x-\frac{L}{2}- L_b\right)}\mathrm dx = -\frac{F^2\hbar^2\kappa^2}{2m} \int_L^{L+L_b}e^{-\kappa \left(x-\frac{L}{2}\right)} e^{\kappa \left(x-\frac{L}{2}- L_b\right)} \mathrm dx \\ & -\frac{F^2\hbar^2\kappa^2}{2m} \int_L^{L+L_b}e^{-\kappa \left(x-\frac{L}{2}\right) + \kappa \left(x-\frac{L}{2} - L_b\right)} = -\frac{F^2\hbar^2\kappa^2}{2m} \int_L^{L+L_m}e^{-\kappa L_b x}\mathrm dx = -\frac{F^2\hbar^2\kappa^2}{2m}L_be^{-\kappa L_b } \end{aligned}
For E_1, F=G and the root is coming from the tangent. The result is that \Delta E is a negative quantity.
Computing now H_{21}, and applying the same arguments:
\begin{aligned} H_{21} = & \int_{-\infty}^\infty \bar \psi_R \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R\right)\psi_L \mathrm dx \\ = & \int_{-\infty}^{\text{L}} \bar \psi_R \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R\right)\psi_L \mathrm dx + \int_{\text{barrier}} \bar \psi_R \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R \right)\psi_L \mathrm dx \\& + \int_{\text{R}}^{-\infty} \bar \psi_R \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2} + V_L + V_R\right)\psi_L \mathrm dx = \int_{\text{barrier}} \bar \psi_R \left(-\frac{\hbar^2}{2m} \frac{\mathrm d^2}{\mathrm dx^2}\right)\psi_L \mathrm dx = \Delta \bar E \end{aligned}
With this simplification of the Hamiltonian the previous eigenequation becomes:
\begin{bmatrix} E_1 & \Delta E \\ \Delta \bar E & E_1 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = E\begin{bmatrix} \alpha \\ \beta \end{bmatrix}
And it is possible to compute the characteristic polynomial for the system:
\begin{bmatrix} E_1 - E & \Delta E \\ \Delta \bar E & E_1 - E \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
as:
(E_1-E)^2 + |\Delta E|^2 = 0
which gives as solutions:
E = E_1 \pm |\Delta E|
So the solution for this problem are two energy levels centered around E_1 and separated by an amount 2\Delta E.
Once the eigenvalues are computed, it is possible to compute the eigenvectors; for the state E_1 + |\Delta E|
\begin{bmatrix} -|\Delta E| & \Delta E \\ \Delta \bar E & - |\Delta E| \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
which gives:
\alpha = \beta
So the first not normalized wavefunction is:
\psi_1 = \psi_L + \psi_R
For the state E_1 + |\Delta E|
\begin{bmatrix} |\Delta E| & \Delta E \\ \Delta \bar E & |\Delta E| \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
which gives:
\alpha = -\beta
So the second not normalized wavefunction is:
\psi_2 = \psi_L - \psi_R
Since the functions are the same, the normalized version is:
\begin{aligned} & \psi_1 = \frac{1}{\sqrt 2}\left(\psi_L + \psi_R\right) \\ & \psi_2 = \frac{1}{\sqrt 2}\left(\psi_L - \psi_R\right) \end{aligned}
The wavefunction \psi_2 = \frac{1}{\sqrt{2}}(\psi_L - \psi_R) is characterized by having opposite signs. The overall sign of this wavefunction is arbitrary; for instance, flipping the sign would still yield a valid solution. Conversely, the wavefunction \psi = \frac{1}{\sqrt{2}}(\psi_L + \psi_R) has the same sign, having both negative would also be a valid solution, the important point is that the sign is the same.
These functions can be plotted:
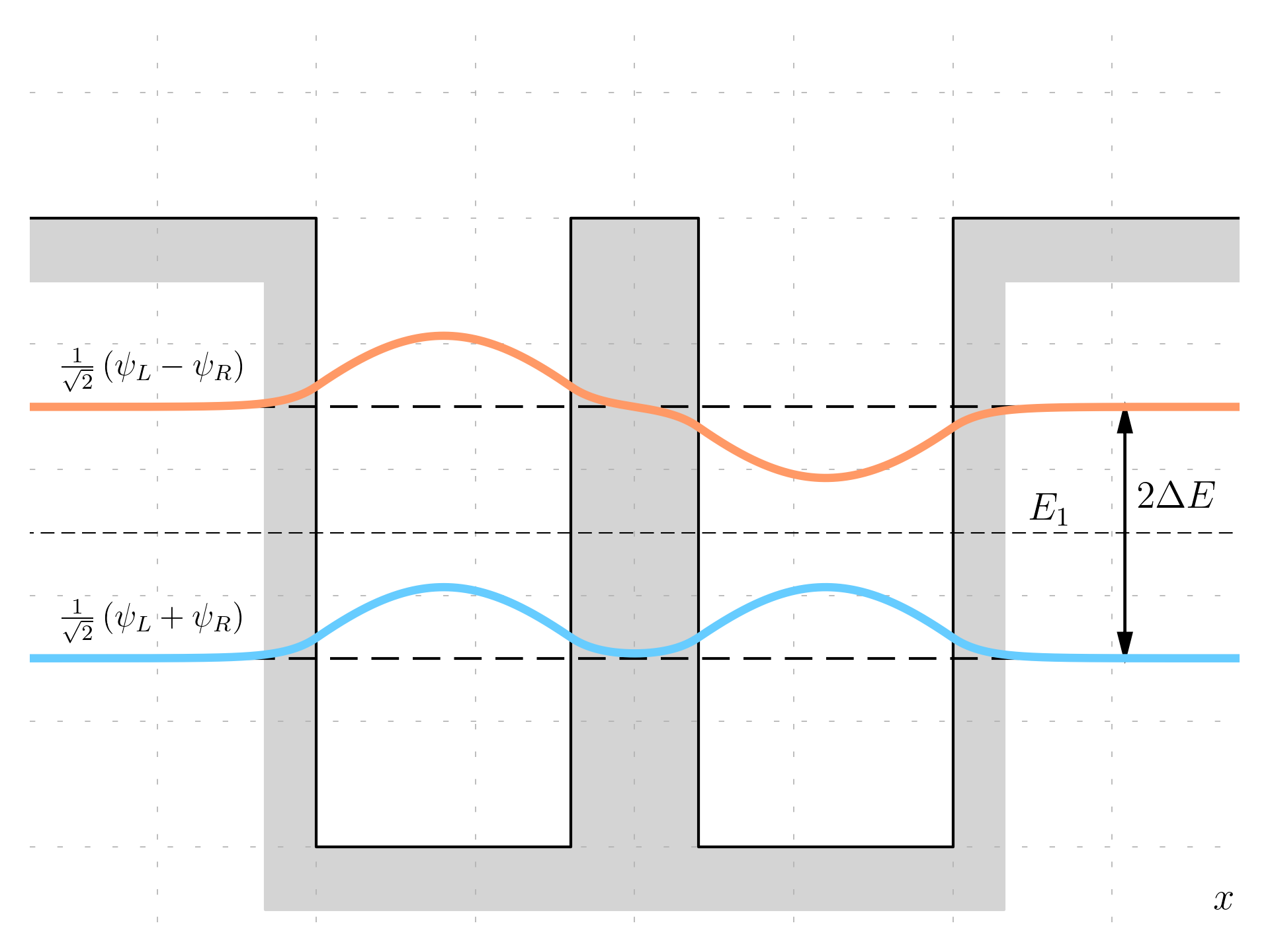
The lower energy state is a symmetric linear combination of the single-well wavefunctions, In this state, the wavefunction \psi_1 maintains the same sign in both wells, indicating a symmetric state. This describes the electron being delocalized, equally present in both wells, differing from the uncoupled case where the electron was localized to one well. The upper energy state is an anti-symmetric combination, the wavefunction has opposite signs in the two wells, signifying an anti-symmetric state. Similar to the lower energy state, the electron is equally present in both wells, indicating the effects of coupling between the wells.
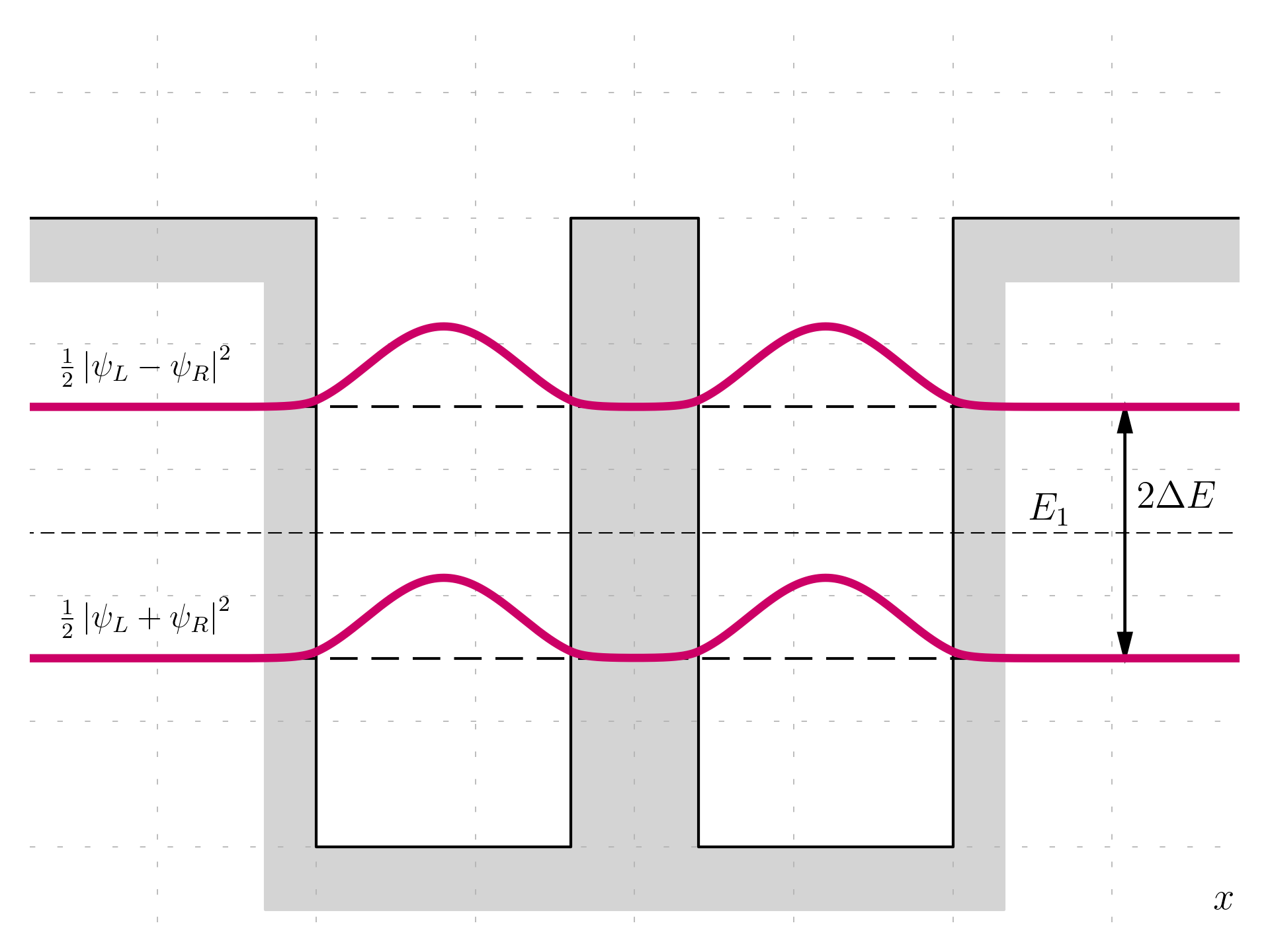
The probability distribution for both the symmetric and anti-symmetric eigenfunctions is derived by squaring the wavefunction, which removes any signs of asymmetry between the left and right wells. Thus, it is defined as follows:
For the symmetric state:
P = |\psi|^2 = \left|\frac{1}{\sqrt{2}}(\psi_L + \psi_R)\right|^2 = \frac{1}{2}|\psi_L + \psi_R|^2
For the anti-symmetric state:
P = |\psi|^2 = \left|\frac{1}{\sqrt{2}}(\psi_L - \psi_R)\right|^2 = \frac{1}{2}|\psi_L - \psi_R|^2
In both cases, the probability distribution P shows that the electron is equally likely to be found in either well, confirming that the physical results remain unchanged regardless of the sign or phase of the wavefunction.