Finite potential well
Considering a potential V(x) such as:
V(x) = \begin{cases} V_0 & \quad x \le -\frac{L}{2} \\ 0 & \quad x > -\frac{L}{2}, x < -\frac{L}{2} \\ V_0 & \quad x \ge \frac{L}{2} \end{cases}
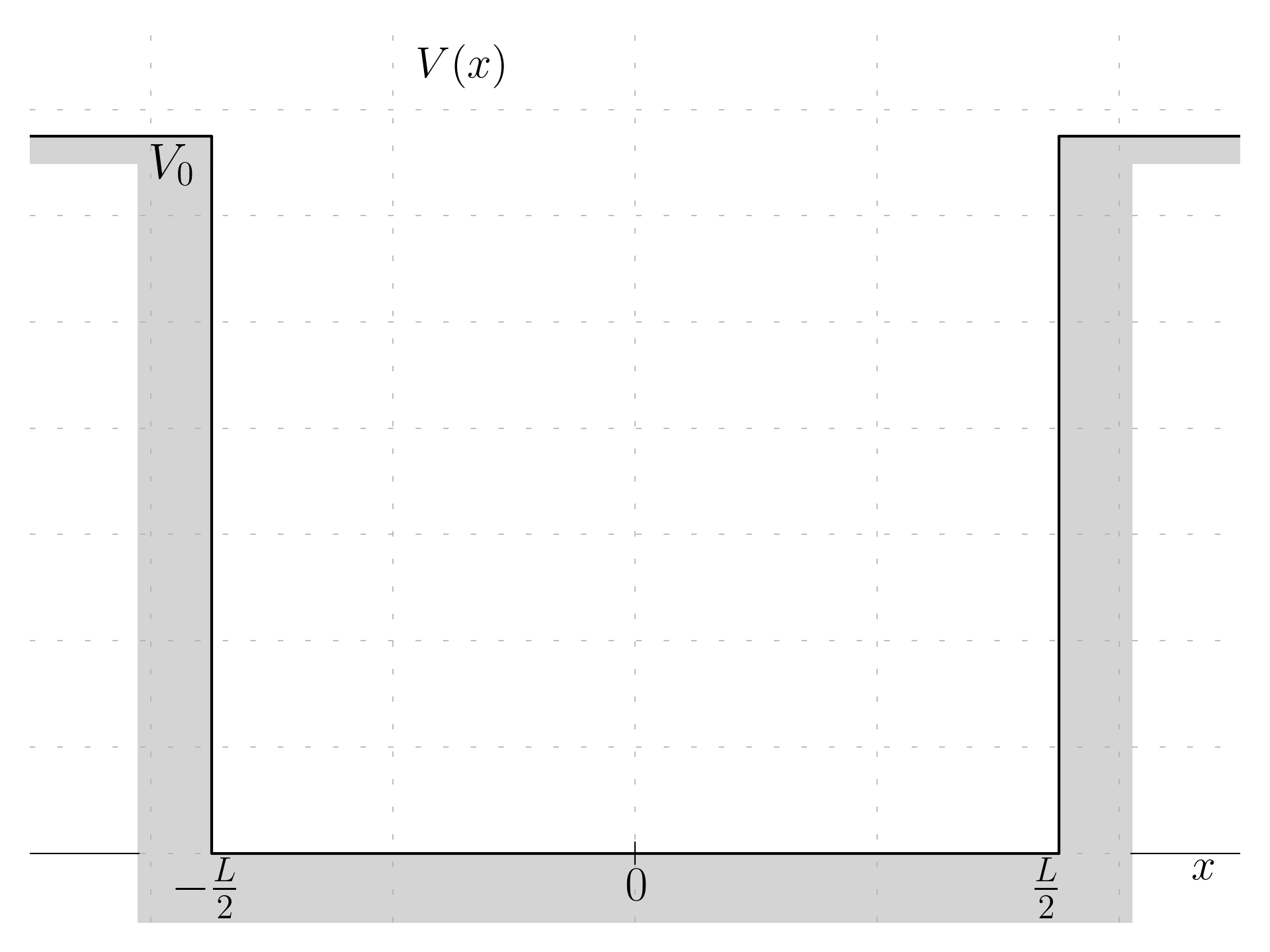
Compared with the particle in a box example (here), the origin is now in the center of the well, so that the well goes from -\frac{L}{2} to \frac{L}{2}; that is just for the algebra to be easier to write down.
If there are solutions to this problem, they will be sinusoidal or cosinusoidal shape in the middle and exponential decaying on the side, discarding the exponentially growing solution as it is physically possible.
If these solutions exist, then the constant k and \kappa would be:
\begin{aligned} & k = \sqrt{\frac{2mE}{\hbar^2}} \\ & \kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}} \end{aligned}
For x <-\frac{L}{2} the solution would be of the form:
\psi(x) = G\, e^{\kappa x}
The sign is kept positive because x<0.
For -\frac{L}{2}< x < \frac{L}{2} the solution would be of the form:
\psi(x) = A\,\sin(kx) + B\,\cos(kx)
Finally, for x >\frac{L}{2} the solution would be of the form:
\psi(x) = F\, e^{-\kappa x}
with the constants A,B,G,F yet to be determined, using the boundary conditions.
Starting from the continuity on the right of the well:
\begin{aligned} & F\, e^{-\kappa\frac{L}{2}} \equiv F\,X_L \\ & A\,\sin\left(k\frac{L}{2}\right) + B\,\cos\left(k\frac{L}{2}\right) \equiv A\,S_L + B\,C_L\\ & F\,X_L = A\,S_L + B\,C_L \end{aligned}
Similarly, at x = -\frac{L}{2} (since \cos(-x) = \cos(x) and \sin(-x) = - \sin(x):
G\,X_L = -A\,S_L + B\,C_L
Applying the continuity of the derivatives at x = -\frac{L}{2}:
-\frac{\kappa}{k}F\,X_L = A\,C_L - B\,S_L
and at x = -\frac{L}{2}:
\frac{\kappa}{k}G\,X_L = A\,C_L + B\,S_L
So there are four equations:
\begin{aligned} & F\,X_L = A\,S_L + B\,C_L \\ & G\,X_L = -A\,S_L + B\,C_L \\ &-\frac{\kappa}{k}F\,X_L = A\,C_L - B\,S_L \\ &\frac{\kappa}{k}G\,X_L = A\,C_L + B\,S_L \end{aligned}
Adding the first two equations and subtracting the last two:
\begin{aligned} & 2B\,C_L = (F + G)X_L \\ & 2B\,S_L = \frac{\kappa}{k}(F+G)X_L \end{aligned}
As long as F \ne -G it is possible to divide the second equation above by the first one:
\frac{S_L}{C_L} = \frac{\sin\left(k\frac{L}{2}\right)}{\cos\left(k\frac{L}{2}\right)} = \tan\left(k\frac{L}{2}\right) = \frac{\kappa}{k}
This relations will allow to compute the energy eigenvalues.
Returning to the four equations, subtracting the first two and adding the last two:
\begin{aligned} & 2A\,C_L = (F - G)X_L \\ & 2A\,S_L = -\frac{\kappa}{k}(F-G)X_L \end{aligned}
As long as F \ne G it is possible to divide the second equation above by the first one with a minus sign:
-\frac{S_L}{C_L} = -\frac{\cos\left(k\frac{L}{2}\right)}{\sin\left(k\frac{L}{2}\right)} = -\cot\left(k\frac{L}{2}\right) = \frac{\kappa}{k}
This is also a condition on the eigenvalues.
For any case other than F=G or F=-G (for which one of the above relationship doesn’t hold) it would appear that:
\begin{aligned} & \tan\left(k\frac{L}{2}\right) = \frac{\kappa}{k} \\ & -\cot\left(k\frac{L}{2}\right) = \frac{\kappa}{k} \end{aligned}
But these are contradictory, and therefore the only solutions is that F=G or F=-G.
For the condition F = G, this condition applies:
\tan\left(k\frac{L}{2}\right) = \frac{\kappa}{k}
From these equations:
\begin{aligned} & 2A\,C_L = (F - G)X_L = 0 \\ & 2A\,S_L = -\frac{\kappa}{k}(F-G)X_L = 0 \end{aligned}
Since \sin(\theta) and \cos(\theta) cannot be zero, and the same time, then:
A = 0
And therefore in the well the solution is \propto \cos(kx), which is an even function.
For the condition F = -G, this condition applies:
-\cot\left(k\frac{L}{2}\right) = \frac{\kappa}{k}
From these equations:
\begin{aligned} & 2B\,C_L = (F + G)X_L = 0 \\ & 2B\,S_L = \frac{\kappa}{k}(F+G)X_L = 0 \end{aligned}
Since again \sin(\theta) and \cos(\theta) cannot be zero, and the same time, then:
B = 0
And therefore in the well the solution is \propto \sin(kx), which is an odd function.
The solutions are not yet computed, to compute the energy it is necessary to solve for:
\begin{aligned} & \tan\left(k\frac{L}{2}\right) = \frac{\kappa}{k} \\ & -\cot\left(k\frac{L}{2}\right) = \frac{\kappa}{k} \end{aligned}
and that can be done only numerically. Considering a dimensionless energy \epsilon \equiv \frac{E}{E_1^\infty} with:
E_1^\infty = \frac{\hbar^2}{2m}\left(\frac{\pi}{L}\right)^2
which is the first level of energy of the infinite potential well, and a dimensionless height \nu_0 \equiv \frac{V_0}{E_1^\infty}, which gives:
\begin{aligned} & k = \sqrt{\frac{2mE}{\hbar^2}} = \frac{\pi}{L} \sqrt \epsilon \\ & \kappa = \sqrt{\frac{2m\left(V_0 - E\right)}{\hbar^2}} = \frac{\pi}{L} \sqrt {\nu_0 - \epsilon} \\ \end{aligned}
Consequently:
\begin{aligned} & \frac{\kappa}{k} = \sqrt {\frac{\nu_0 - \epsilon}{\epsilon}} \\ & k\frac{L}{2} = \frac{\pi}{2} \sqrt \epsilon \\ & \kappa\frac{L}{2} = \frac{\pi}{2} \sqrt {\nu_0 - \epsilon} \end{aligned}
The equation to solve will become:
\begin{aligned} & \sqrt{\epsilon} \tan\left(\frac{\pi}{2}\sqrt{\epsilon} \right) = \sqrt {\nu_0 - \epsilon} \\ & -\sqrt{\epsilon} \cot\left(\frac{\pi}{2}\sqrt{\epsilon}\right) = \sqrt {\nu_0 - \epsilon} \end{aligned}
This can be graphically solved; first a specific well depth \nu_0 is chosen, then the curve \sqrt{v_0 - \epsilon} is plot.
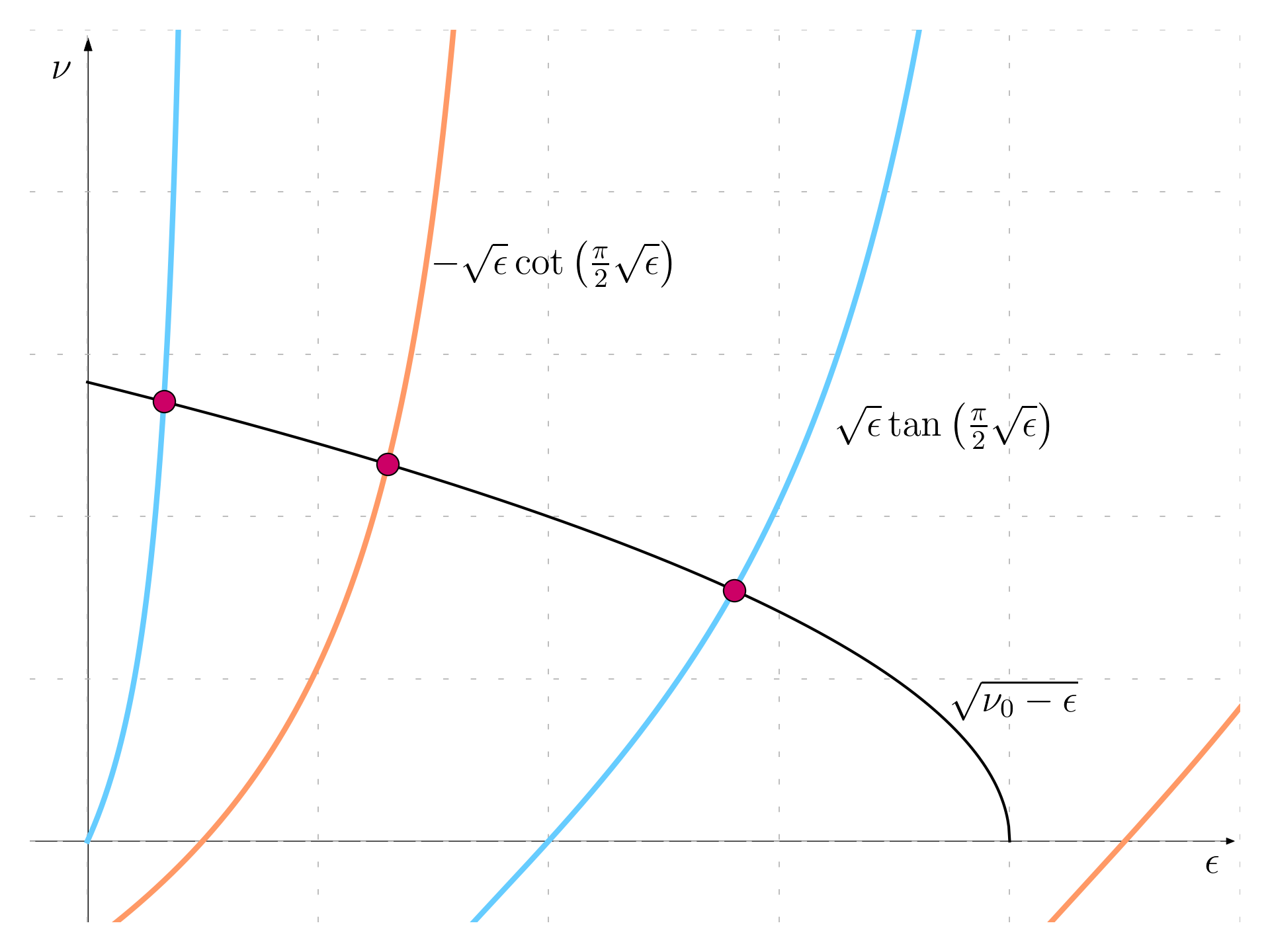
For example, considering \nu_0 = 8, three solutions are identified with the following values:
\begin{array}{|c|c|c|} \hline \nu & \epsilon & root \\ \hline 2.70872601 & 0.66280341 & \tan \\ 2.32304517 & 2.60346113 & \cot \\ 1.54639923 & 5.60864943 & \tan \\ \hline \end{array}
Once the level is computed, then it is possible to compute the solutions using the normalization condition.
For the case in which F = G then normalization condition is:
\int_{-\infty}^{-\frac{L}{2}} F^2 e^{2\kappa x} dx + \int_{-\frac{L}{2}}^{\frac{L}{2}} B^2 \cos^2(kx) dx + \int_{\frac{L}{2}}^{\infty} G^2 e^{-2\kappa x} dx = 1
Then solving these integrals:
\frac{F^2e^{2\kappa L}}{2\kappa} + \frac{B^2(kL - \sin(kL))}{2k} + \frac{F^2e^{-2\kappa L}}{2\kappa} = 1
Since:
\begin{aligned} & 2B\,C_L = (F + G)X_L = 2F\,X_L \\ & F = B\frac{\cos\left(k\frac{L}{2}\right)}{e^{-\kappa\frac{L}{2}}} \end{aligned}
It is possible to compute B:
B = \sqrt{\frac{2k\kappa e^{\kappa L}}{Lk\kappa e^{\kappa L} + k e^{4\kappa L}\cos^2\left(\frac{Lk}{2}\right) + k\cos^2\left(\frac{Lk}{2}\right) - \kappa e^{\kappa L}\sin(Lk)}}
And then substituting back for getting F and G=F.
For the case in which F = -G then normalization condition is:
\int_{-\infty}^{-\frac{L}{2}} F^2 e^{2\kappa x} dx + \int_{-\frac{L}{2}}^{\frac{L}{2}} A^2 \sin^2(kx) dx + \int_{\frac{L}{2}}^{\infty} G^2 e^{-2\kappa x} dx = 1
Then solving it:
\frac{F^2e^{2\kappa L}}{2\kappa} + \frac{A^2}{2}\left(L - \frac{\sin(kL)}{k}\right) + \frac{F^2e^{-2\kappa L}}{2\kappa} = 1
Since:
\begin{aligned} & 2A\,C_L = (F - G)X_L = 2F\,X_L \\ & F = A\frac{\sin\left(k\frac{L}{2}\right)}{e^{-\kappa\frac{L}{2}}} \end{aligned}
It is possible to compute A:
A = \sqrt{\frac{2k\kappa e^{\kappa L}}{Lk\kappa e^{\kappa L} + k e^{4\kappa L}\sin^2\left(\frac{Lk}{2}\right) + k\sin^2\left(\frac{Lk}{2}\right) - \kappa e^{\kappa L}\sin(Lk)}}
And then substituting back for getting F and G=-F.
The results are plotted below (in this example A and B were set as parameter and not computed).
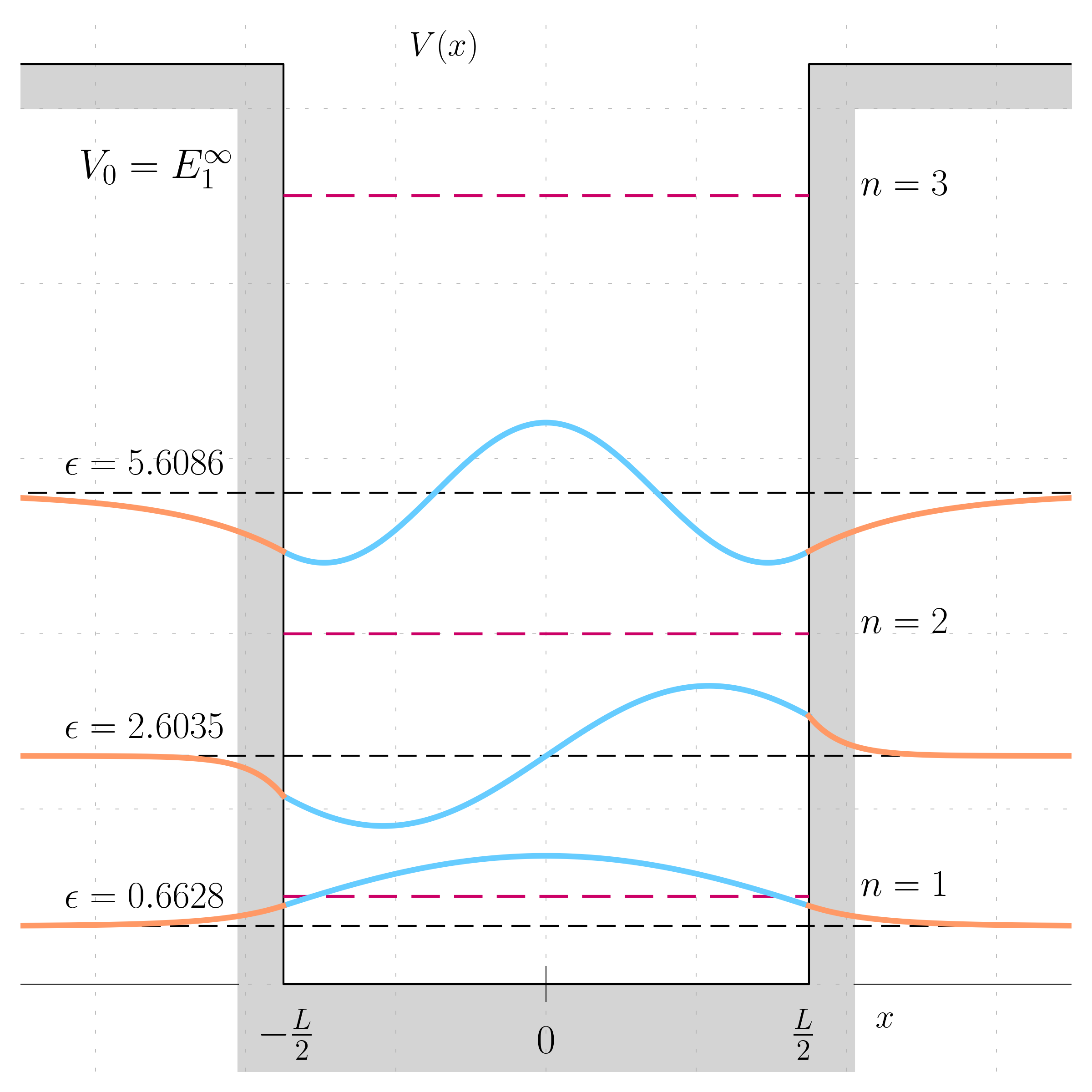
There are only three solution for this depth. An interesting point to note is that, comparing with the solution that would have been obtained with an infinite deep well, they are at a lower level, the first one is at 0.6628 compared to the first energy of the infinite well, and the same is true for n=2 and n=3 (these three values are also superposed on the same graph).
In the infinite potential well, a full half period of a sinusoidal or cosinusoidal would fit, but the result on the finite potential is less curved, an therefore has less kinetic energy.