Effective Mass Theory
In general, it is common to have a local minima or maxima around k=0, and at least Kramers degeneracy ensure that the point is stationary, as it is necessary to be symmetric; silicon or germanium for example do not have for k=0, but, since it is a repeated curve, it must have point of minimum and maximum.
These are in any case extremely important, because electron (in the conduction band) and holes (in the valence) band, tend to concentrate around these points, and consequently it is important to have model that can approximate the behavior around these points; one of these model is the effective mass approximation.
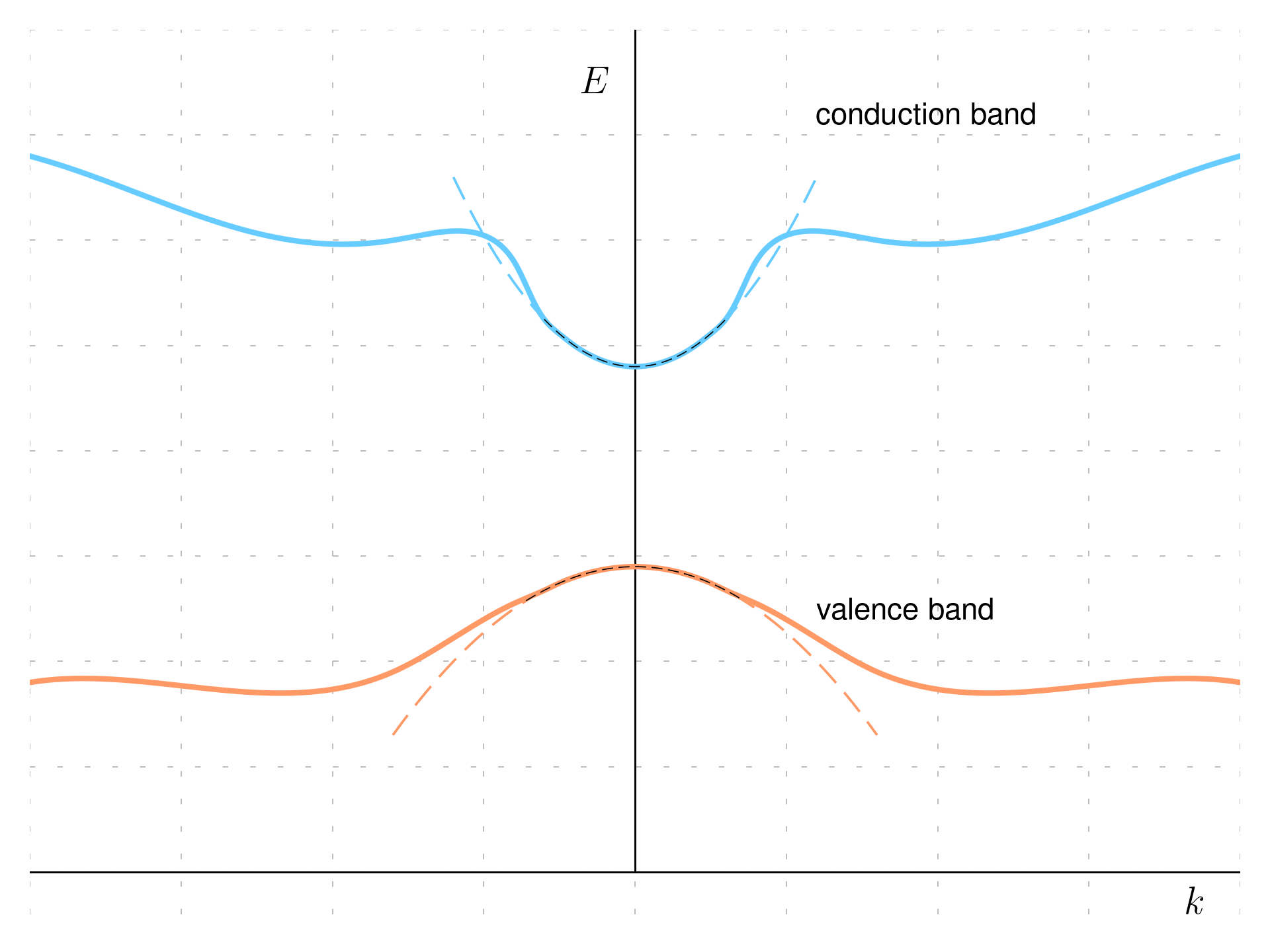
In the neighborhood of these stationary points, the energy variation can be approximated with a parabola. At first we will assume that the variation is isotropic around \mathbf k=0 for simplicity (like the case for direct gap semiconductors), but we will be later making an example where the location of the stationary point is \mathbf k_m \ne 0 (for indirect gap semiconductors like silicon or germanium).
If the energy at the stationary point is V, then the energy for the wavevector \mathbf k is:
E_k - V \propto \mathbf k^2 \equiv \frac{\hbar^2 k^2}{2m_{eff}}
so the proportionality constant has been chosen in this way, so the effective mass m_{eff} is the inverse proportionality constant that satisfy the relationship; this approximation is called isotropic parabolic band.
Since the energy is proportional to the square, as for the case of wavepackets (here) the solution will show a pulse that is moving through space. Let’s consider a linear superposition of Bloch states in a single band:
\Psi(\mathbf r,t) = \sum_k c_k u_k(\mathbf r) e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t}
There is the assumption that this superposition is only of a small range of \mathbf k around 0, so that for these range u_k(\mathbf r) \cong u_0(\mathbf r):
\Psi(\mathbf r,t) = u_0(\mathbf r) \Psi_{env}
where:
\Psi_{env} \equiv \sum_k c_k e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t}
Differentiating with respect of time gives a Schrödinger equation for the envelope.
\begin{aligned} i\hbar\frac{\partial \Psi_{env}}{\partial t} & = \sum_k c_k E_k e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} = \sum_k c_k \left( \frac{\hbar^2k^2}{2m_{eff}} + V \right) e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} \\ & = \sum_k c_k \frac{\hbar^2k^2}{2m_{eff}} e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} + \sum_k c_k V e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} \\ & = \frac{\hbar^2}{2m_{eff}} \sum_k -c_k \nabla^2e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} + V \Psi_{env} \\ & = -\frac{\hbar^2}{2m_{eff}} \nabla^2 \Psi_{env} + V \Psi_{env} \end{aligned}
This is a Schrödinger equation for the envelope:
i\hbar\frac{\partial \Psi_{env}(\mathbf r,t)}{\partial t} = -\frac{\hbar^2}{2m_{eff}} \nabla^2 \Psi(\mathbf r,t)_{env} + V(\mathbf r) \Psi_{env}(\mathbf r,t)
Therefore the electron can be treated as a particle with an effective mass m_{eff} that obeys the envelope wavefunction, there is no longer any reference to the periodic potential nor unit cell wavefunction. However, it does not mean that the mass of the electron itself is changed; the electron still obeys the Schrödinger equation with a periodic potential, the effective mass theory gives the equation for the envelope, which behave like a particle.
There is a further approximation since V(\mathbf r) is no longer constant (in the derivation V is the value at the stationary point) but we allowed a central potential, and that is true only if this change in potential with the distance is sufficiently small, and this, despite not being theoretical justified, it is a model that works sufficient well in practical situations and agree with experimental results.
A similar derivation can made for a band which is centered in another point \mathbf k_m and the energy is (\Delta k^2 = (\mathbf k - \mathbf k_m)^2):
E_k = \frac{\hbar\Delta k^2}{2m_{eff}} + V
Let’s again consider a linear superposition of Bloch states in a single band:
\Psi(\mathbf r,t) = \sum_k c_k u_k(\mathbf r) e^{i\mathbf k \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t}
There is the assumption that this superposition is only of a small range of \mathbf k around \mathbf k_m this time, so that for these range u_k(\mathbf r) \cong u_m(\mathbf r):
\Psi(\mathbf r,t) = u_m(\mathbf r) \Psi_{env}
where:
\Psi_{env} \equiv \sum_k c_k e^{i(\mathbf k - \mathbf k_m) \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} as the envelope is now centered in \mathbf k_m. Differentiating with respect of time gives a Schrödinger equation for the envelope.
\begin{aligned} i\hbar\frac{\partial \Psi_{env}}{\partial t} & = \sum_k c_k E_k e^{i(\mathbf k - \mathbf k_m) \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} = \sum_k c_k \left( \frac{\hbar^2\Delta k^2}{2m_{eff}} + V \right) e^{i(\mathbf k - \mathbf k_m) \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} \\ & = \sum_k c_k \frac{\hbar^2\Delta k^2}{2m_{eff}} e^{i(\mathbf k - \mathbf k_m) \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} + \sum_k c_k V e^{i(\mathbf k - \mathbf k_m) \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} \\ & = \frac{\hbar^2}{2m_{eff}} \sum_k -c_k \nabla^2e^{i(\mathbf k - \mathbf k_m) \cdot \mathbf r}e^{\frac{-iE_k}{\hbar}t} + V \Psi_{env} \\ & = -\frac{\hbar^2}{2m_{eff}} \nabla^2 \Psi_{env} + V \Psi_{env} \end{aligned}
This is the same Schrödinger equation for the envelope as before:
i\hbar\frac{\partial \Psi_{env}(\mathbf r,t)}{\partial t} = -\frac{\hbar^2}{2m_{eff}} \nabla^2 \Psi(\mathbf r,t)_{env} + V(\mathbf r) \Psi_{env}(\mathbf r,t)