Wavepackets

Wavepackets

In discussions about waves, we typically assume they move at a constant speed, denoted as v or c. However, in many cases, especially with classical waves like sound or light, different frequencies can travel at varying speeds. This effect, known as dispersion, might be minimal in straightforward scenarios but can significantly impact certain situations. Dispersion is particularly pronounced in quantum mechanics, where understanding group velocity is crucial to grasp how fast wave packets move. Let’s explore deeper dispersion and group velocity.

Group velocity

Considering two waves of distinct frequencies, \omega_1 and \omega_2, we assume their velocities (v) remain consistent, unaffected by frequency changes. The wave vector magnitude, k, is given by the ratio \omega/v, applicable to both waves. Thus, for wave one, k_1 = \omega_1 / v, and for wave two, k_2 = \omega_2 / v.

When these two waves, assumed to have equal amplitudes, are combined, the result is a composite wave exhibiting spatial beats. These beats form an envelope pattern overlaying the merged wave, moving at the same velocity as the individual waves.

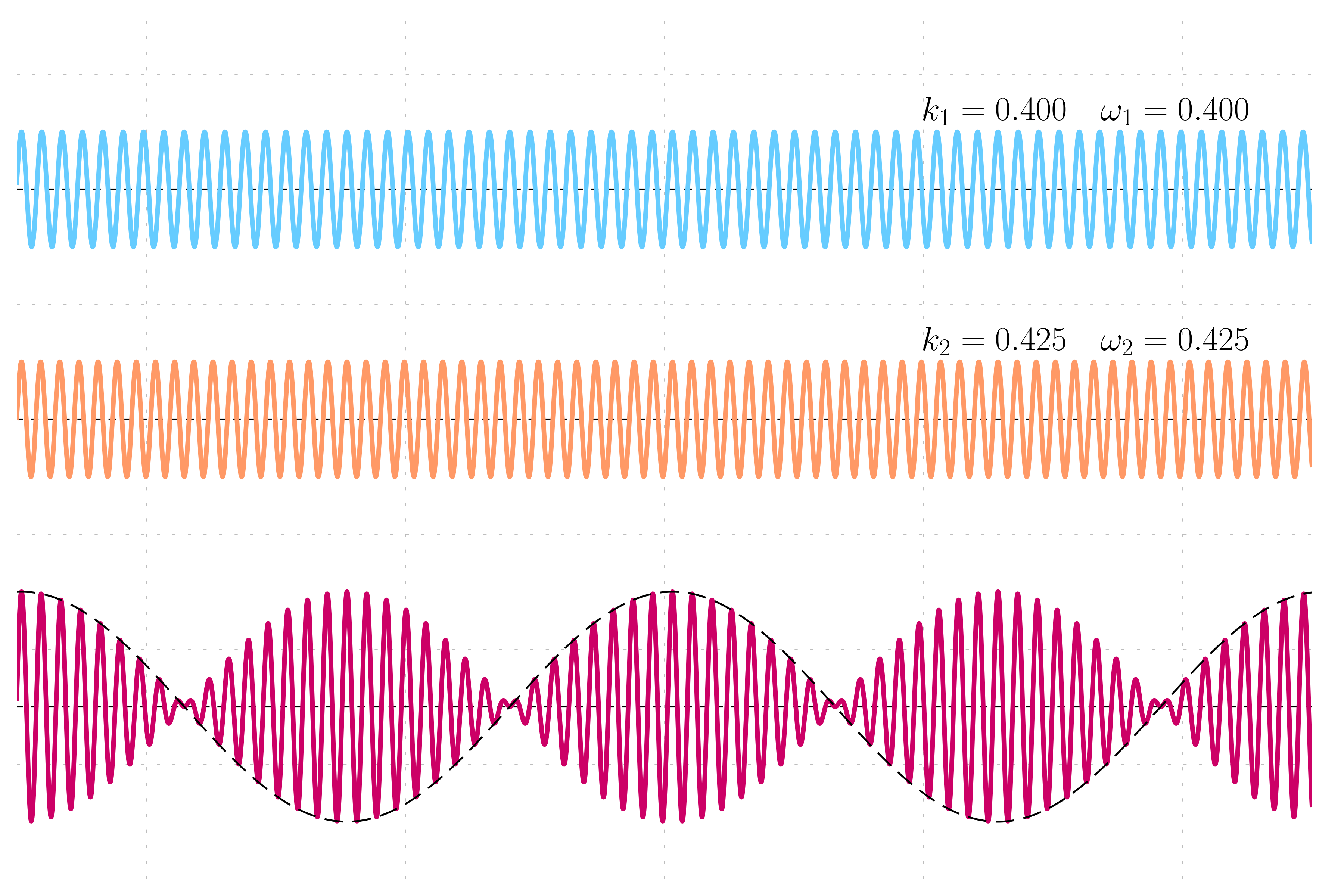
For the first wave with a frequency of 0.4 units, its k vector is also 0.4 units due to the chosen velocity. The second wave, with a frequency of 0.425 units, similarly has a k vector magnitude of 0.425 units. The combination of these two waves (blue and orange) generates a third wave (magenta), characterized by an envelope (indicated by a dashed line) that signifies the spatial beats, a direct consequence of their linear superposition.

Given two waves with frequencies \omega + \delta\omega and \omega - \delta\omega, and wave vectors k + \delta k and k - \delta k respectively, using complex exponential notation, the total wave f(z, t) can be represented as the sum of these two waves:

f(x, t) = e^{-i(\omega + \delta\omega)t - (k + \delta k)x} + e^{-i(\omega - \delta\omega)t - (k - \delta k)x}

Factoring out the common term e^{-i\omega t - kx}, we get:

f(x, t) = e^{-i\omega t - kx}\left[e^{-i\delta\omega t - \delta kx} + e^{i\delta\omega t + \delta kx}\right]

Recognizing the sum inside the parentheses as the expression for 2\cos(\delta\omega t - \delta kx), the formula simplifies to:

f(z, t) = 2e^{-i\omega t - kx}\cos(\delta\omega t - \delta kx)

Given that k = \frac{\omega}{v}, it implies v = \frac{\omega}{k}. Hence, \delta k = \frac{\delta \omega}{v}, and the velocity of the envelope, v_{\text{envelope}}, is \frac{\delta \omega}{\delta k}. This means the envelope moves with velocity v_{\text{envelope}} = \frac{\delta \omega}{\delta k}. The underlying wave propagates at velocity v_{\text{wave}} = \frac{\omega}{k}.

In this scenario, both the envelope and the wave propagate at the same velocity, given by the ratios \frac{\delta \omega}{\delta k} and \frac{\omega}{k}, respectively. This means the envelope’s movement, represented by the cosine term, and the exponential wave itself advance at identical speeds. However, if wave velocity varies with frequency—specifically, if higher frequency waves travel slower, resulting in a disproportionately higher k (since k = \frac{\omega}{v}), we see a change. A slower velocity (v) leads to a larger k value, indicating more wave crests within the same distance. This adjustment in wave spacing affects the envelope’s velocity, denoted as \frac{\delta \omega}{\delta k}, which we will refer to as the group velocity.

Group velocity is defined more precisely as the limit of \frac{\delta \omega}{\delta k} as both \delta k and \delta \omega approach zero. Group velocity (v_g) is mathematically expressed as \frac{\mathrm d\omega}{\mathrm dk}. This concept is widely applicable in determining the effective velocity of pulses or wave packets in dispersive media.

For clarity, the ratio \frac{\omega}{k}, which denotes the velocity of the underlying wave at a specific frequency, is referred to as the phase velocity (v_p). Therefore, group velocity, \frac{\mathrm d\omega}{dk}, represents the velocity of the envelope (the dashed line), while the phase velocity, corresponds to the velocity of the underlying wave (the magenta line).

Electron wavepackets

In most situation with classical waves, the effect of group velocity has a small effect or one important under relative extreme conditions, but in quantum mechanics plays a central role, because, for waves associated with particles, an electron for example, the phase velocity and the group velocity are almost never the same.

For a free electron, the frequency \omega is not proportional to the wavevector magnitude k; considering the case V(x) = 0, the Schrödinger equation is:

-\frac{\hbar^2}{2m} \frac{\mathrm d^2\psi(x)}{\mathrm d x^2} = E\psi(x)

which has a solution:

\psi(x) \propto e^{\pm i k x} \quad E = \frac{\hbar^2k^2}{2m}

so the energy is proportional to k^2, so the frequency associated is:

\omega = \frac{E}{\hbar} = \frac{\hbar k^2}{2m}

so \omega \propto k^2 and \omega \not\propto k and it is possible to compute the free electron group velocity:

v_g = \frac{\mathrm d \omega}{\mathrm d k} = \frac{1}{\hbar} \frac{\mathrm d E}{\mathrm d k} = \frac{\hbar k}{m} = \sqrt{\frac{2}{m}\frac{\hbar^2 k^2}{m}} = \sqrt{\frac{E}{2m}}

so, computing the energy from this formula:

E = \frac{1}{2}mv_g^2

which correspond to the classical definition of kinetic energy, suggesting that the electron is moving at the group velocity.

Looking that the phase velocity, it does not gives the same kind of relationship, as it is simply:

v_p = \frac{\omega}{k} = \frac{hk}{2m} = 2v_g

so:

v_p^2 = \frac{h^2k^2}{4m^2} = \frac{1}{2m}\frac{h^2k^2}{2m} = \frac{E}{2m}

And therefore:

E = 2mv_p^2

which does not correspondent to the classical relationship and therefore the electron moves at the group velocity v_g.

It is possible to construct a wavepacket of electrons putting together a linear superposition of energy eigensolutions; for a free particle, those eigensolutions are plain waves of the form:

\Psi(x,t) \propto e^{-i\left(\frac{E(k)}{\hbar}t - kx\right)} = e^{-i\left(\omega(k) - kx\right)}

with:

E(k) = \frac{\hbar^2k^2}{2m} \quad \omega(k) = \frac{E(k)}{\hbar}

One set of k and a_k that can be chosen is a set of equally spaced value with a Gaussian amplitude:

\Psi_g(x,t) \propto \sum_k e^{-\left(\frac{k - \bar k}{2\Delta k}\right)^2}e^{-i\left(\omega(k)t - kx\right)}

The resulting wave is a smooth function with a peak in the middle, \bar k is the average, and \Delta k is the width parameter for the Gaussian function; this peak is not only visible in the frequencies domains, but also in the spatial domain (since a Fourier transform of a Gaussian is still a Gaussian). It is then possible to have this curve moving in time, and inside each component (which is itself a plane wave) has its own oscillation frequency, so the result is a sum of these waves.

The wave packet moves and it gets wider (it is dispersing) as it went; the center is indeed moving at the group velocity v_g; it gets wider in this case because the change in \omega is not linear with k (in this case is quadratic) and this effect is known as group velocity dispersion; furthermore the group velocity itseld is a function of k.

The wave function can be represented in various ways. One common method is to separate it into its real and imaginary components, and plot the modulus (absolute value) of the wave function below.

Alternatively, the wave function can be visualized by plotting the modulus and using a color-coded phase to represent the complex number.

These different visual representations are equivalent, providing complementary insights into the behavior and properties of the wave packet.