Quantization Light One Mode
Traveling Plane Electromagnetic Wave
Traveling Plane Electromagnetic Wave
Standing Wave
Traveling Waves superpositions
Harmonic oscillator recap
The starting point is the quantum description of the harmonic oscillator (which is described in details here), as the quantized radiation behaves like a set of quantized harmonic oscillators.
Using the creation (\mathbf a^\dag) and annihilation (\mathbf a) operators and the number operator (\mathbf N = \mathbf a^\dag \mathbf a), the Hamiltonian can be written as:
\mathbf H = \hbar \omega\left(\mathbf a^\dag \mathbf a + \frac{1}{2}\right) = \hbar \omega\left(\mathbf N + \frac{1}{2}\right)
This formalism has the advantage that is no longer dependent from the specific problem being analyzed, and the solutions are valid for any harmonic oscillator.
These relations hold:
\begin{aligned} & \mathbf N | \psi_n \rangle = n | \psi_n \rangle \\ & \mathbf a^\dag | \psi_n \rangle = \sqrt{n+1} | \psi_{n+1} \rangle \\ & \mathbf a | \psi_n \rangle = \sqrt n | \psi_{n-1} \rangle \\ & \mathbf a | \psi_0 \rangle = \mathbf a | \mathbf 0 \rangle = 0 \end{aligned}
It worth remembering that \| | \psi_0 \rangle \| = \| | \mathbf 0 \rangle \| = 1, so it has a unitary length, and should not be confused with the null vector with has a norm 0.
Considering the energy level (or equivalently the eigenvalues of the Hamiltonian:
\mathbf H | \psi_n \rangle = E | \psi_n \rangle
Then applying the number operator, the expression of the energy of the Harmonic oscillator is found:
E_n = \hbar\omega \left(n + \frac{1}{2}\right), \quad n \in \mathbb N
Using the creation operator it is possible to derive any state from the ground state:
| \psi_n \rangle = \frac{\left(\mathbf a^\dag\right)^n}{\sqrt {n!}} | \mathbf 0 \rangle
The ground state | \mathbf 0 \rangle has interesting property, as its energy is not null, but it is \frac{\hbar\omega}{2}. And this is not an arbitrary energy level, it is the energy at the bottom of the harmonic oscillator.
In this position, the average of dimensionless position and momentum are null:
\begin{aligned} \langle \xi \rangle & = \langle \mathbf 0 | \xi | \mathbf 0 \rangle = \frac{1}{\sqrt 2}\langle \mathbf 0 | \mathbf a + \mathbf a\dag | \mathbf 0 \rangle = \frac{1}{\sqrt 2}\left[\langle \mathbf 0 | \left(\mathbf a | \mathbf 0 \rangle \right) + \langle \left(\mathbf 0 | \mathbf a\dag \right) | \mathbf 0 \rangle \right] = 0 \\ \langle i\frac{\mathrm d}{\mathrm d \xi} \rangle & = \langle \mathbf 0 | i\frac{\mathrm d}{\mathrm d \xi} | \mathbf 0 \rangle = -\frac{i}{\sqrt 2}\langle \mathbf 0 | \mathbf a - \mathbf a\dag | \mathbf 0 \rangle = -\frac{i}{\sqrt 2}\left[\langle \mathbf 0 | \left(\mathbf a | \mathbf 0 \rangle \right) - \langle \left(\mathbf 0 | \mathbf a\dag \right) | \mathbf 0 \rangle \right] = 0 \end{aligned}
But does not means that the oscillator is static, there is a dispersion, as it can be shown computing the standard deviation.
\begin{aligned} \langle \xi^2 \rangle & = \langle \mathbf 0 | \xi^2 | \mathbf 0 \rangle = \frac{1}{2}\langle \mathbf 0 | \left( \mathbf a + \mathbf a\dag \right)^2 | \mathbf 0 \rangle = \frac{1}{2}\langle \mathbf 0 | \left( \mathbf a^2 + \mathbf a \mathbf a^\dag + \mathbf a^\dag + \left(\mathbf a\dag\right)^2 \right) | \mathbf 0 \rangle\\ & = \frac{1}{2}\left[ \langle \left(\mathbf 0 |\mathbf a^2 \right) | \mathbf 0 \rangle + \langle \mathbf 0 |\mathbf a \mathbf a^\dag | \mathbf 0 \rangle + \left( \langle \mathbf 0 |\mathbf a^\dag \right) | \mathbf 0 \rangle + \left(\langle \mathbf 0 | \left(\mathbf a\dag\right)^2 \right) | \mathbf 0 \rangle \right] \\ & = \frac{1}{2}\langle \mathbf 0 |\mathbf a \mathbf a^\dag | \mathbf 0 \rangle = \frac{1}{2}\langle \mathbf 0 |\left(1 + \mathbf a^\dag \mathbf a\right) | \mathbf 0 \rangle = \frac{1}{2} \\ \langle \left( i\frac{\mathrm d}{\mathrm d \xi} \right)^2 \rangle & = \langle \mathbf 0 | \left( i\frac{\mathrm d}{\mathrm d \xi} \right)^2 | \mathbf 0 \rangle = -\frac{1}{2}\langle \mathbf 0 | \left( \mathbf a - \mathbf a\dag \right)^2 | \mathbf 0 \rangle = \frac{1}{2}\langle \mathbf 0 | \left( \mathbf a^2 - \mathbf a \mathbf a^\dag - \mathbf a^\dag + \left(\mathbf a\dag\right)^2 \right) | \mathbf 0 \rangle\\ & = -\frac{1}{2}\left[ \langle \left(\mathbf 0 |\mathbf a^2 \right) | \mathbf 0 \rangle - \langle \mathbf 0 |\mathbf a \mathbf a^\dag | \mathbf 0 \rangle - \left( \langle \mathbf 0 |\mathbf a^\dag \right) | \mathbf 0 \rangle + \left(\langle \mathbf 0 | \left(\mathbf a\dag\right)^2 \right) | \mathbf 0 \rangle \right] \\ & = \frac{1}{2}\langle \mathbf 0 |\mathbf a \mathbf a^\dag | \mathbf 0 \rangle = \frac{1}{2}\langle \mathbf 0 |\left(1 + \mathbf a^\dag \mathbf a\right) | \mathbf 0 \rangle = \frac{1}{2} \end{aligned}
Since the oscillator spread symmetrical around zero, it means that both the potential and the kinetic energy are not null in this ground state, there are vacuum fluctuations.
This is another occurrence of the Heisenberg principle which state that there is a minimum precision that can be known for the conjugate variables position and momentum. Moving from dimensionless to dimensional variables and computing the variance:
\begin{aligned} & \Delta \mathbf x^2 = \frac{\hbar}{m\omega}\langle \mathbf 0 | \xi^2 | \mathbf 0 \rangle = \frac{1}{2}\frac{\hbar}{m\omega} \\ & \Delta \mathbf p^2 = \hbar m \omega\langle \left( i\frac{\mathrm d}{\mathrm d \xi} \right)^2 \rangle = \frac{1}{2}\hbar m \omega \end{aligned}
The uncertainty principle relation for the ground state is:
\Delta \mathbf x \Delta \mathbf p = \sqrt{\Delta \mathbf x^2 \Delta \mathbf p^2} = \frac{\hbar}{2}
This is the lowest value permitted from the uncertainty principle, and therefore the ground state has the minimum possible fluctuation and it is called the minimum dispersion state.
Traveling plane electromagnetic wave
Let’s consider the Maxwell equations in a source-free environment. This scenario represents situations where the typical sources of electromagnetic fields, such as charges or currents, are either absent, effectively turned off, or located far away from the volume of interest. Such conditions are often encountered in theoretical studies or in practical applications where the influence of distant sources like stars or radio wave transmitters is considered negligible. In this source-free context, the equations describe the propagation of electromagnetic waves through a vacuum or other media without the direct influence of external sources.
\begin{aligned} &\nabla \cdot \mathbf E(\mathbf r, t) = 0 \\ &\nabla \cdot \mathbf B(\mathbf r, t) = 0 \\ &\nabla \times \mathbf E(\mathbf r, t) = -\frac{\partial \mathbf B(\mathbf r, t)}{\partial t} \\ &\nabla \times \mathbf B(\mathbf r, t) = \mu_0 \epsilon_0 \frac{\partial \mathbf E(\mathbf r, t)}{\partial t} \end{aligned}
In these cases, the only crucial information needed is the value of the electromagnetic field at the boundaries. By knowing the boundary conditions, we can determine the behavior and evolution of the fields within the volume of interest. This allows us to solve for the fields everywhere in the region, even in the absence of sources, providing a complete description of the electromagnetic phenomena in the specified area.
The simplest solutions in such scenarios are called modes, which are fields oscillating at specific frequencies. These modes represent stable patterns of electromagnetic fields that can exist in the absence of sources. By analyzing these modes, we can understand the natural frequencies and resonances of the system, which are critical in many practical applications such as waveguides, resonant cavities, and antenna design.
Electric field
Since these modes oscillate, they can be quantized as harmonic oscillators. In the quantum mechanical framework, each mode corresponds to a quantized oscillator, with discrete energy levels.
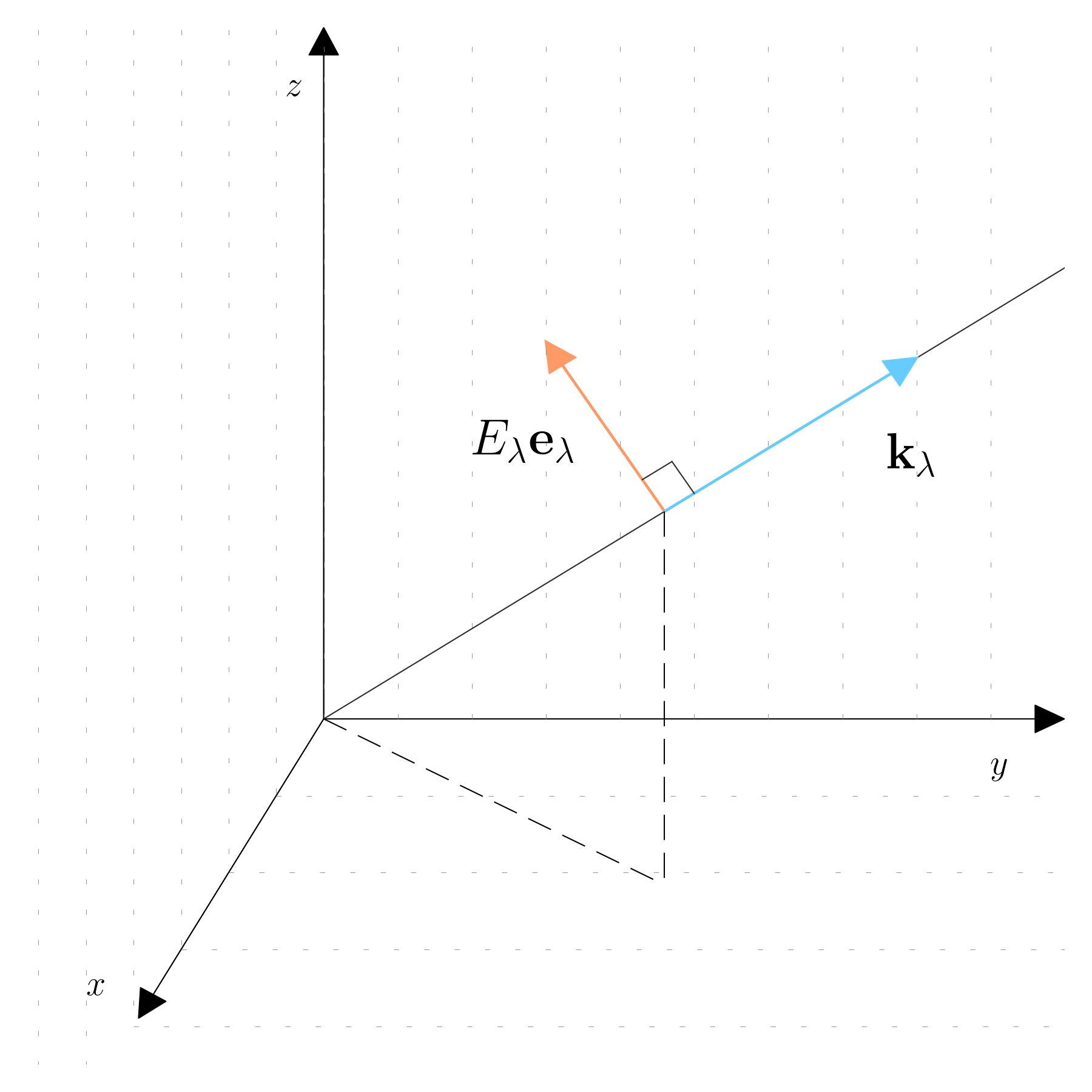
Let’s consider a traveling propagating plane wave:
\mathbf E(\mathbf r, t) = E_\lambda(t) \mathbf e_\lambda e^{i \mathbf k_\lambda \cdot \mathbf r} + E_\lambda(t) \mathbf e_\lambda e^{-i \mathbf k_\lambda \cdot \mathbf r}
where:
- E_\lambda(t) is the amplitude of the wave;
- \mathbf e_\lambda is the polarization vector, indicating the direction of the electric field;
- \mathbf k_\lambda is the wave vector, describing the direction and wavelength of the wave.
This expression represents a plane wave traveling in the direction of \mathbf k_\lambda with a specific polarization and amplitude. The terms with e^{i \mathbf k_\lambda \cdot \mathbf r} and e^{-i \mathbf k_\lambda \cdot \mathbf r} indicate the forward and backward traveling components of the wave, respectively.
There are some conditions that need to be fulfilled, first the complex conjugate ensures that the field is real.
The polarization vector \mathbf e_\lambda must be perpendicular to the wave vector \mathbf k_\lambda to satisfy the condition \nabla \cdot \mathbf E = 0. This ensures that the electric field is divergence-free, which is a requirement for a source-free Maxwell equation.
Another requirement is that the electric field \mathbf E oscillates at a frequency \omega_\lambda given by the dispersion relation:
\omega_\lambda = c k_\lambda
where:
- \omega_\lambda is the angular frequency of the wave,
- c is the speed of light in a vacuum,
- k_\lambda = |\mathbf k_\lambda| is the magnitude of the wave vector.
This relation ensures that the wave propagates correctly in free space, maintaining the proper phase relationship between the oscillating electric field and the wave vector.
This solution:
\mathbf E(\mathbf r, t) = E_\lambda(t)\mathbf e_\lambda e^{i \mathbf k_\lambda \cdot \mathbf r} + E_\lambda(t) \mathbf e_\lambda e^{-i \mathbf k_\lambda \cdot \mathbf r}
represents a polarized plane monochromatic wave, satisfying all the necessary conditions.
Magnetic field
To fully describe the dynamics of the electromagnetic field, it is necessary to find two canonical conjugate variables that describe the amplitude of the field. Returning to the Maxwell equations, the second and third equations tell us that the magnetic field \mathbf{B} must also be perpendicular to both \mathbf E and \mathbf k:
\mathbf B(\mathbf r, t) = B_\lambda(t)\mathbf b_\lambda e^{i \mathbf k_\lambda \cdot \mathbf r} + B_\lambda(t) \mathbf e_\lambda e^{-i \mathbf k_\lambda \cdot \mathbf r}
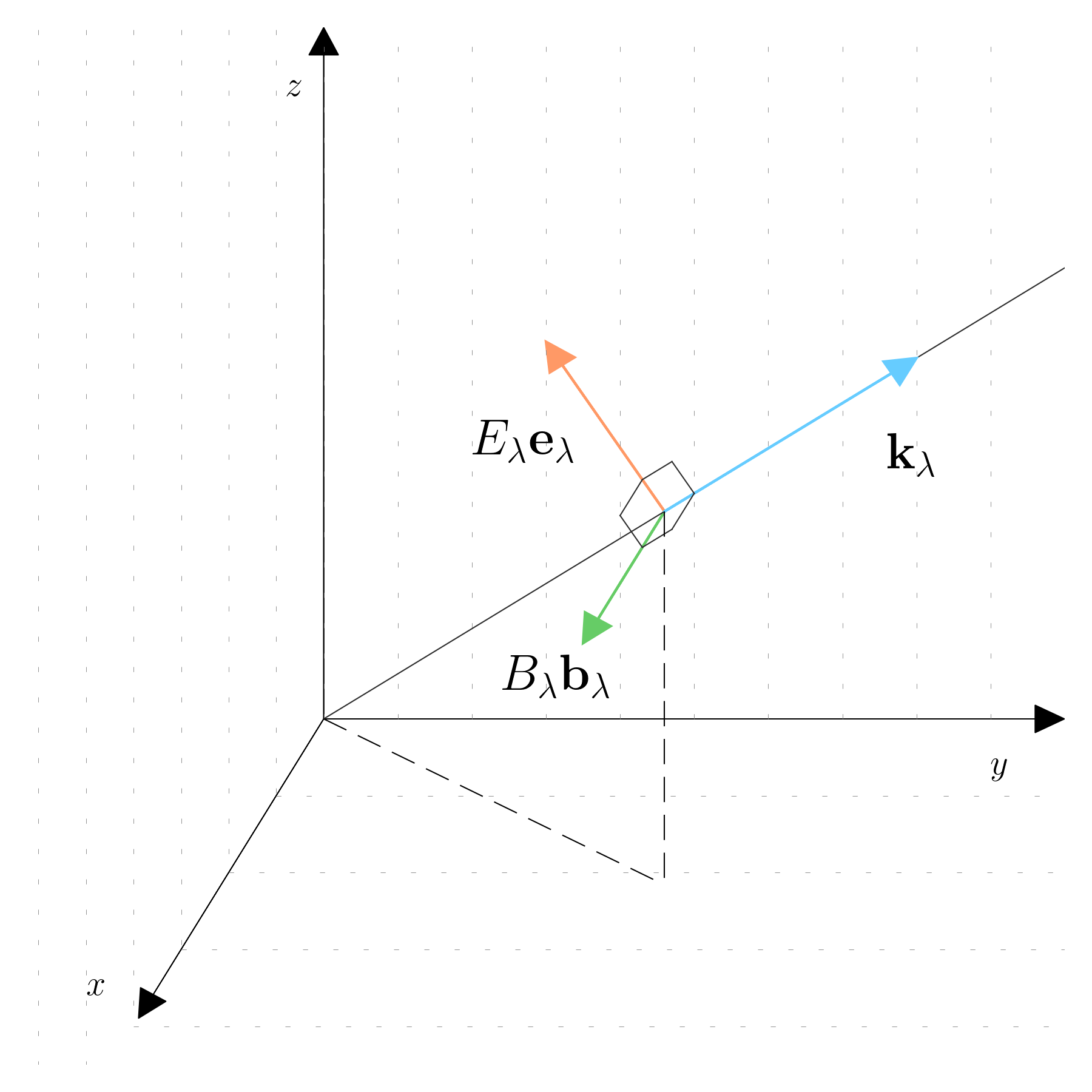
The resulting expression for \mathbf{B} is:
\mathbf B (\mathbf r, t) = \frac{1}{\omega_\lambda^2} (\mathbf k_\lambda \times \mathbf e_\lambda) \frac{\mathrm d E_\lambda(t)}{\mathrm dt} e^{i \mathbf k_\lambda \cdot \mathbf r} + \frac{1}{\omega_\lambda^2} (\mathbf k_\lambda \times \mathbf e_\lambda) \frac{\mathrm d E_\lambda(t)}{\mathrm dt} e^{-i \mathbf k_\lambda \cdot \mathbf r}
This expression ensures that the magnetic field \mathbf{B} is correctly oriented and oscillates in accordance with the electric field and wave vector.
Taking the time derivative of \mathbf{B}(\mathbf{r}, t):
\frac{\partial \mathbf{B}(\mathbf{r}, t)}{\partial t} = \frac{1}{\omega_\lambda^2} (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) \frac{\mathrm d^2 E_\lambda(t)}{\mathrm dt^2} e^{i \mathbf{k}_\lambda \cdot \mathbf{r}} + \frac{1}{\omega_\lambda^2} (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) \frac{\mathrm d^2 E_\lambda(t)}{\mathrm dt^2} e^{-i \mathbf{k}_\lambda \cdot \mathbf{r}}
Using the second Maxwell equation \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}:
For \mathbf{E}(\mathbf{r}, t):
\nabla \times \mathbf{E} = i (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) E_\lambda(t) e^{i \mathbf{k}_\lambda \cdot \mathbf{r}} + i (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) E_\lambda(t) e^{-i \mathbf{k}_\lambda \cdot \mathbf{r}}
Equating both sides:
i (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) E_\lambda(t) e^{i \mathbf{k}_\lambda \cdot \mathbf{r}} + i (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) E_\lambda(t) e^{-i \mathbf{k}_\lambda \cdot \mathbf{r}} = - \frac{1}{\omega_\lambda^2} (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) \frac{\mathrm d^2 E_\lambda(t)}{\mathrm dt^2} e^{i \mathbf{k}_\lambda \cdot \mathbf{r}} - \frac{1}{\omega_\lambda^2} (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) \frac{\mathrm d^2 E_\lambda(t)}{\mathrm dt^2} e^{-i \mathbf{k}_\lambda \cdot \mathbf{r}}
Since (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) is non-zero, we obtain:
i E_\lambda(t) e^{i \mathbf{k}_\lambda \cdot \mathbf{r}} + i E_\lambda(t) e^{-i \mathbf{k}_\lambda \cdot \mathbf{r}} = - \frac{1}{\omega_\lambda^2} \frac{\mathrm d^2 E_\lambda(t)}{\mathrm dt^2} e^{i \mathbf{k}_\lambda \cdot \mathbf{r}} - \frac{1}{\omega_\lambda^2} \frac{\mathrm d^2 E_\lambda(t)}{\mathrm dt^2} e^{-i \mathbf{k}_\lambda \cdot \mathbf{r}}
Simplifying and equating coefficients, we get the second-order differential equation for E_\lambda(t):
\frac{\mathrm d^2 E_\lambda(t)}{\mathrm dt^2} = -\omega_\lambda^2 E_\lambda(t)
This confirms that E_\lambda(t) oscillates at the angular frequency \omega_\lambda, satisfying the harmonic oscillator equation.
The characteristic roots that can be found by solving the characteristic equation associated with this differential equation:
r^2 + \omega_\lambda^2 = 0
Solving for r:
r = \pm i \omega_\lambda
This gives the general solution to the differential equation in the form:
E_\lambda(t) = A e^{i \omega_\lambda t} + B e^{-i \omega_\lambda t}
We take the derivative of E_\lambda(t):
\frac{\mathrm d E_\lambda(t)}{\mathrm dt} = A i \omega_\lambda e^{i \omega_\lambda t} - B i \omega_\lambda e^{-i \omega_\lambda t} = \pm i \omega_\lambda E_\lambda(t)
Where \pm i \omega_\lambda represents the two possible solutions based on the characteristic roots.
The constants can be retrieved by the initial conditions as t=0 and general solution to this equation can be written as:
E_\lambda(t) = E_\lambda(0) e^{i \omega_\lambda t} + E_\lambda(0) e^{-i \omega_\lambda t}
To represent a wave traveling in a specific direction, we choose one of the solutions. For a wave traveling along \mathbf{k}_\lambda, we use the solution with the negative exponent:
E_\lambda(t) = E_\lambda(0) e^{-i \omega_\lambda t}
Thus, the electric field \mathbf{E}(\mathbf{r}, t) can be written as:
\mathbf{E}(\mathbf{r}, t) = E_\lambda(0) \mathbf{e}_\lambda e^{i (\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} + E_\lambda(0) \mathbf{e}_\lambda e^{-i (\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)}
Similarly the magnetic field:
\mathbf{B}(\mathbf{r}, t) = \frac{1}{\omega_\lambda} (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) E_\lambda(0) e^{i (\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} + \frac{1}{\omega_\lambda} (\mathbf{k}_\lambda \times \mathbf{e}_\lambda) E_\lambda(0) e^{-i (\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)}
Since \mathbf{e}_\lambda is a unit vector perpendicular to \mathbf{k}_\lambda:
|\mathbf{k}_\lambda \times \mathbf{e}_\lambda| = |\mathbf{k}_\lambda| |\mathbf{e}_\lambda| \sin(90^\circ) = |\mathbf{k}_\lambda|
Given that |\mathbf{k}_\lambda| = k_\lambda = \frac{\omega_\lambda}{c}, we have:
|\mathbf{k}_\lambda \times \mathbf{e}_\lambda| = \frac{\omega_\lambda}{c}
As the complex part has unitary modulus, the modulus of the magnetic field is:
|\mathbf{B}(\mathbf{r}, t)| = \frac{1}{\omega_\lambda}\frac{\omega_\lambda}{c}|E_\lambda(0)| = \frac{|E_\lambda(0)|}{c}
The two equations can also be expressed (factorizing the amplitude varying with time) as:
\begin{aligned} & \mathbf{E}(\mathbf{r}, t) = E_\lambda(t) \mathbf{e}_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} + \text{c.c.} \\ & \mathbf{B}(\mathbf{r}, t) = \frac{\mathbf{k}_\lambda \times \mathbf{e}_\lambda}{\omega_\lambda} E_\lambda(t) e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} +\text{c.c.} \end{aligned}
where \text{c.c.} is a shorthand for the complex conjugate so that the resulting function are real.
Canonical conjugate variables
Lets write the complex amplitude of the electric field defining the normal variable \alpha_\lambda (which is dimensionless) writing:
E_\lambda(t) = i \mathscr E^{(1)}_\lambda \alpha_\lambda(t)
The i factor is arbitrary but it is a choice made by many author in quantum optics, so it is done to keep consistency.
\alpha_\lambda is evolving in time in the same way as E_\lambda:
\frac{\mathrm d \alpha_\lambda(t)}{\mathrm dt} = -i\omega_\lambda \alpha_\lambda(t)
so that:
\alpha_\lambda = \alpha_\lambda(0) e^{-i\omega_\lambda t}
Now we introduce the real and imaginary part of \alpha (the factor is to simplify formulas at a later stage):
\begin{aligned} & \alpha_\lambda(t) = \frac{1}{\sqrt {2\hbar}}\left(Q_\lambda + iP_\lambda\right) \\ & Q = \Re{(\alpha_\lambda)} = \sqrt{\frac{\hbar}{2}}\left(\alpha_\lambda(t) + \bar \alpha_\lambda(t)\right) \\ & P = \Im{(\alpha_\lambda)} = \sqrt{\frac{\hbar}{2}}\left(\alpha_\lambda(t) - \bar \alpha_\lambda(t)\right) \end{aligned}
The energy of the mode can be written as:
\mathcal H_\lambda = \frac{\epsilon_0}{2} \int_{V_\lambda}\left( \mathbf E^2 + c^2 \mathbf B^2\right) \mathrm d\mathbf r^3
For a running wave the magnetic field magnitude as demonstrated is |\mathbf B| = \frac{\mathbf E}{c} and therefore:
\mathcal H_\lambda = \epsilon_0 \int_{V_\lambda} \mathbf E^2 \mathrm d\mathbf r^3 = 2\epsilon_0 \int_{V_\lambda} \left| \mathbf E_\lambda^2 \right| \mathrm d\mathbf r^3 = 2\epsilon_0 V_\lambda \left| \mathbf E_\lambda^2 \right| = 2\epsilon_0 V_\lambda \left( \mathscr E^{(1)}_\lambda \right)^2 \left| \alpha_\lambda^2(t) \right|
The factor of 2 is coming from the definition of the complex amplitude (as there is the complex conjugated function to be taken into account as well). V_\lambda is the quantization volume. This volume were the radiation is considered: if there is a cavity it is a true volume bounded by mirrors (for example) which impose boundary conditions. For a wave expanding to infinity in all directions, since the function is periodic, it is possible to apply periodic boundary conditions.
The constant \mathscr E^{(1)}_\lambda (called one photon amplitude of the mode \lambda) is chosen as:
\mathscr E^{(1)}_\lambda = \sqrt{\frac{\hbar \omega_\lambda}{2\epsilon_0 V_\lambda}}
It is the amplitude of a field that has the energy \hbar \omega_\lambda in the quantization volume V_\lambda (that is immediately verified:
\mathcal H_\lambda = 2\epsilon_0 V_\lambda \left( \mathscr E^{(1)}_\lambda \right)^2 \left| \alpha_\lambda^2(t) \right| = 2\epsilon_0 V_\lambda \frac{\hbar \omega_\lambda}{2\epsilon_0 V_\lambda} \left| \alpha_\lambda^2(t) \right| = \hbar \omega_\lambda \left| \alpha_\lambda^2(t) \right|
This choice (even for the semiclassical approximation) is due to the fact that we will soon quantize this field, and therefore is natural to consider \hbar\omega_\lambda as the characteristic value of the energy for this problem.
Using the real and imaginary part of \alpha(t) it becomes:
\mathcal H_\lambda = \hbar \omega_\lambda \left| \alpha_\lambda^2(t) \right| = \hbar \omega_\lambda\frac{1}{2\hbar}\left(Q_\lambda^2 + P_\lambda^2\right) = \frac{\omega_\lambda}{2}\left(Q_\lambda^2 + P_\lambda^2\right)
This is an harmonic oscillator, and it is now possible to perform the canonical quantization of the field in the mode \lambda.
In the case of plane wave, we can then apply the periodic boundary conditions, considering a cube with side of length L and taking this length to be is an integer multiple of \mathbf k:
\begin{aligned} & k_{\lambda,x} = 2\pi n_{\lambda,x} \\ & k_{\lambda,y} = 2\pi n_{\lambda,y} \\ & k_{\lambda,z} = 2\pi n_{\lambda,z} \end{aligned}
n_{\lambda,i} can take any positive or negative value in order to span the full space.
It is possible to apply Hamilton equations to the two variables P_\lambda and Q_\lambda:
\begin{aligned} \frac{\mathrm dQ_\lambda}{\mathrm dt} & = \frac{\partial \mathcal H}{\partial P} = \omega_\lambda P \\ \frac{\mathrm dP_\lambda}{\mathrm dt} & = -\frac{\partial \mathcal H}{\partial Q} = -\omega_\lambda Q \end{aligned}
Taking the time derivatives of \alpha_\lambda and use these relationships:
\frac{\mathrm d\alpha_\lambda(t)}{\mathrm dt} =\frac{1}{\sqrt {2\hbar}}\frac{\mathrm d}{\mathrm dt}\left(Q_\lambda + iP_\lambda\right) = -i\omega_\lambda \frac{1}{\sqrt {2\hbar}}\left(Q_\lambda + iP_\lambda\right)= -i\omega_\lambda \alpha_\lambda(t)
Since this equations is the same obtained from Maxwell’s equations, it shows that these are canonically conjugates variables.
Field quantization
It is possible to apply the canonical quantization, defining two operator as:
\begin{aligned} & \mathbf Q = \sqrt{\frac{\hbar}{2}}\left(\mathbf a + \mathbf a^\dag\right) \\ & \mathbf P = -i\sqrt{\frac{\hbar}{2}}\left(\mathbf a - \mathbf a^\dag\right) \\ & [\mathbf Q, \mathbf P] = i \hbar \end{aligned}
The quantized Hamiltonian becomes:
\mathbf H = \frac{\omega_\lambda}{2}\left(\mathbf Q_\lambda^2 + \mathbf P_\lambda^2\right)
This is an Harmonic oscillator, we then introduce the equivalent quantization of \alpha and \bar \alpha:
\begin{aligned} & \mathbf a_\lambda = \frac{1}{\sqrt {2\hbar}}\left(\mathbf Q_\lambda + i\mathbf P_\lambda\right) \\ & \mathbf a_\lambda^\dag = \frac{1}{\sqrt {2\hbar}}\left(\mathbf Q_\lambda - i\mathbf P_\lambda\right) \\ \end{aligned}
Their commutator is:
[\mathbf a_\lambda, \mathbf a_\lambda^\dag] = 1
retrieving \mathbf Q_\lambda and \mathbf P_\lambda from the definitions, and use the commutator relations, give the Hamiltonian:
\mathbf H_\lambda = \hbar \omega_\lambda\left(\mathbf a_\lambda\mathbf a_\lambda^\dag + \frac{1}{2}\right)
Observables
\mathbf a_\lambda and \mathbf a_\lambda^\dag are one the Hermitian conjugate of the other; being non-Hermitian, they are not observables but they are important because all the observables can be expressed as function of them. \mathbf Q_\lambda and \mathbf P_\lambda were used for the derivation of the Hamiltonian:
\begin{aligned} & \mathbf Q_\lambda = \sqrt {\frac{\hbar}{2}} \left(\mathbf a_\lambda + \mathbf a_\lambda^\dag\right)\\ & \mathbf P_\lambda = i \sqrt {\frac{\hbar}{2}} \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) \end{aligned}
Then the electric and magnetic field:
\begin{aligned} & \mathbf{E}(\mathbf{r}) = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \\ & \mathbf{B}(\mathbf{r}) = i\frac{\mathbf{k}_\lambda \times \mathbf{e}_\lambda}{\omega_\lambda} \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \end{aligned}
Since this is the Schrödinger representation, the operators are not varying with time, but the state |\psi(t)\rangle is the one which is varying; once this state is known, the average of the observables can be computed. The average of the field is:
\langle \mathbf E(\mathbf r) \rangle (t) = \langle \psi(t) | \mathbf E(\mathbf r) | \psi(t) \rangle
This average might evolve with time. It is possible to compute the the vacuum fluctuations and how they vary with time:
(\Delta E)^2(t) = \langle \psi(t) | \mathbf E^2(\mathbf r) | \psi(t) \rangle -\left(\langle \mathbf E(\mathbf r) \rangle (t)\right)^2
It is not possible to directly measure the average value of the electric field for visible light, as the frequency are extremely high and even modern detectors give just a zero average; it is however possible to measure the observables \mathbf Q_\lambda and \mathbf P_\lambda with photo-detectors using the homodyne detection technique even for visible light and this is a good substitute for the observation of the field, since it can be express as function of these operators:
\begin{aligned} \mathbf{E}(\mathbf{r}, t) = & i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \\ = & i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[\frac{1}{\sqrt {2\hbar}}\left(\mathbf Q_\lambda - i\mathbf P_\lambda\right) e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \frac{1}{\sqrt {2\hbar}}\left(\mathbf Q_\lambda + i\mathbf P_\lambda\right) e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right] \\ = & \frac{i}{\sqrt {2\hbar}}\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[\left(\mathbf Q_\lambda - i\mathbf P_\lambda\right) e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \left(\mathbf Q_\lambda + i\mathbf P_\lambda\right) e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right] \\ = & \frac{i}{\sqrt {2\hbar}}\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[ \left(e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}}\right) \mathbf Q_\lambda - i\left(e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} + e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}}\right) \mathbf P_\lambda \right] \\ = & \frac{i}{\sqrt {2\hbar}}\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[ \left(\cos(\mathbf{k}_\lambda \cdot \mathbf{r}) +i\sin(\mathbf{k}_\lambda \cdot \mathbf{r}) - \cos(-\mathbf{k}_\lambda \cdot \mathbf{r}) -i\sin(-\mathbf{k}_\lambda \cdot \mathbf{r}) \right) \mathbf Q_\lambda \right. \\ & - \left. i\left(\cos(\mathbf{k}_\lambda \cdot \mathbf{r}) +i\sin(\mathbf{k}_\lambda \cdot \mathbf{r}) + \cos(-\mathbf{k}_\lambda \cdot \mathbf{r}) +i\sin(-\mathbf{k}_\lambda \cdot \mathbf{r}) \right) \mathbf P_\lambda \right] \\ = & \frac{i}{\sqrt {2\hbar}}\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[ \left(\cos(\mathbf{k}_\lambda \cdot \mathbf{r}) +i\sin(\mathbf{k}_\lambda \cdot \mathbf{r}) - \cos(\mathbf{k}_\lambda \cdot \mathbf{r}) + i\sin(\mathbf{k}_\lambda \cdot \mathbf{r}) \right) \mathbf Q_\lambda \right. \\ & - \left. \left(\cos(\mathbf{k}_\lambda \cdot \mathbf{r}) +i\sin(\mathbf{k}_\lambda \cdot \mathbf{r}) + \cos(\mathbf{k}_\lambda \cdot \mathbf{r}) -i\sin(\mathbf{k}_\lambda \cdot \mathbf{r}) \right) \mathbf P_\lambda \right] \\ = & \frac{i}{\sqrt {2\hbar}}\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[2i\sin(\mathbf{k}_\lambda \cdot \mathbf{r}) \mathbf Q_\lambda - 2i\cos(\mathbf{k}_\lambda \cdot \mathbf{r}) \mathbf P_\lambda \right] \\ = & \sqrt {\frac{2}{\hbar}}\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[\cos(\mathbf{k}_\lambda \cdot \mathbf{r}) \mathbf P_\lambda - \sin(\mathbf{k}_\lambda \cdot \mathbf{r}) \mathbf Q_\lambda \right] \end{aligned}
Number states
Knowing the Hamiltonian, it is possible to compute its eigenvalues and eigenvectors, which forms a complete basis of the space of states. The Hamiltonian is the one previously derived:
\mathbf H_\lambda = \hbar \omega_\lambda\left(\mathbf a_\lambda\mathbf a_\lambda^\dag + \frac{1}{2}\right)
Being the Hamiltonian of an harmonic oscillator, the solutions are known (here), and the energies are:
E_{n,\lambda} = \hbar\omega_\lambda \left(n_\lambda + \frac{1}{2}\right), \quad n_\lambda \in \mathbb N
The index \lambda is kept to remind that these are the energies of a specific mode \lambda. It is possible to move from one state to another using the creation and annihilation operations:
\begin{aligned} & \mathbf N_\lambda | \psi_{n,\lambda} \rangle = n_\lambda | \psi_{n,\lambda} \rangle \equiv | \mathbf n_\lambda \rangle \\ & \mathbf a_\lambda^\dag | \psi_{n,\lambda} \rangle = \sqrt{n_\lambda+1} | \psi_{n_\lambda+1} \rangle \\ & \mathbf a_\lambda | \psi_{n,\lambda} \rangle = \sqrt n | \psi_{n_\lambda-1} \rangle \\ & \mathbf a_\lambda | \psi_{0,\lambda} \rangle = \mathbf a_\lambda | \mathbf 0_\lambda \rangle = 0 \end{aligned}
All the states can be generated from the zero state:
| \psi_{n,\lambda} \rangle = \frac{\left(\mathbf a_\lambda^\dag\right)^{n_\lambda}}{\sqrt {n_\lambda!}} | \mathbf 0_\lambda \rangle
These states form a complete set of the system.
The eigenstates | \mathbf n_\lambda \rangle of the number operator are called number state or Fock states.
The number states have a well defined energy which is larger than the quantity of the zero state \frac{1}{2}\hbar \omega_\lambda by:
E_{n,\lambda} - E_{0,\lambda} = n_\lambda \hbar\omega_\lambda
The momentum is defined as:
\mathbf P = \epsilon_0 \int_{V_\lambda}(\mathbf E \times \mathbf B)\mathrm d\mathbf r^3 = |\alpha_\lambda|^2 \hbar \mathbf k_\lambda
The corresponding operator is:
\mathbf P = \hbar \mathbf k_\lambda \mathbf a_\lambda^\dag \mathbf a_\lambda
and therefore the number state is also an eigenstate of the momentum operator:
\mathbf P | \mathbf n_\lambda \rangle = \hbar \mathbf k_\lambda \mathbf a_\lambda^\dag \mathbf a_\lambda | \mathbf n_\lambda \rangle = n_\lambda \hbar \mathbf k_\lambda | \mathbf n_\lambda \rangle
The state | \mathbf n_\lambda \rangle has a well defined energy and momentum:
\begin{aligned} & E_{n,\lambda} - E_{0,\lambda} = n_\lambda \hbar\omega_\lambda \\ & \mathbf P | \mathbf n_\lambda \rangle = n_\lambda \hbar \mathbf k_\lambda | \mathbf n_\lambda \rangle \end{aligned}
It is equivalent to a set of n particles, each one with energy and momentum given by:
\begin{aligned} & E_{\lambda} = \hbar\omega_\lambda \\ & \mathbf P = \hbar \mathbf k_\lambda \end{aligned}
These particles are called photons.
The formula for the momentum is valid for running wave only, different type of wave will have a different formula for the momentum.
Using the relativistic formula for the rest mass:
m^2c^4 = E^2 - P^2c^2 = \hbar^2\omega_\lambda^2 - \hbar^2 k^2_\lambda c^2 = \hbar^2\omega_\lambda^2 - \hbar^2\omega_\lambda^2 = 0
which is consistent with the theory of relativity for a particle which travel at the speed of light has zero mass.
Vacuum fluctuations
In classical physics, the state with no photons (also called vacuum state) has no radiation; in quantum physics, on the other hand, even in the state with no photon, the electromagnetic field has some fluctuations. This is the results already discussed for the harmonic oscillator.
With the electric field:
\mathbf{E}(\mathbf{r}) = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right)
The average is:
\langle \mathbf 0_\lambda | \mathbf{E}(\mathbf{r}) | \mathbf 0_\lambda \rangle = 0
because it there is either a factor \mathbf a_\lambda | \mathbf 0_\lambda \rangle = 0 or \langle \mathbf 0_\lambda | \mathbf a_\lambda^\dag = 0.
The dispersion is however not null:
\begin{aligned} \langle \mathbf 0_\lambda | \mathbf{E}^2(\mathbf{r}) | \mathbf 0_\lambda \rangle & = i^2\left[\mathscr E^{(1)}_\lambda \right]^2 \langle \mathbf 0_\lambda | \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right)^2 | \mathbf 0_\lambda \rangle \\ & = -\left[\mathscr E^{(1)}_\lambda \right]^2 \langle \mathbf 0_\lambda | \left( e^{2i\mathbf{k}_\lambda \cdot \mathbf{r}}\mathbf a_\lambda^2 - \mathbf a_\lambda \mathbf a_\lambda^\dag - \mathbf a_\lambda^\dag\mathbf a_\lambda + e^{-2i\mathbf{k}_\lambda \cdot \mathbf{r}}\left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 0_\lambda \rangle\\ & = \left[\mathscr E^{(1)}_\lambda \right]^2 \left[ -e^{2i\mathbf{k}_\lambda \cdot \mathbf{r}}\langle \mathbf 0_\lambda |\left( \mathbf a^2 | \mathbf 0_\lambda \right) \rangle + \langle \mathbf 0_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 0_\lambda \rangle + \left( \langle \mathbf 0_\lambda |\mathbf a_\lambda^\dag \right) \mathbf a_\lambda | \mathbf 0_\lambda \rangle - e^{-2i\mathbf{k}_\lambda \cdot \mathbf{r}}\left(\langle \mathbf 0_\lambda | \left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 0_\lambda \rangle \right] \\ & = \left[\mathscr E^{(1)}_\lambda \right]^2 \langle \mathbf 0_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 0_\lambda \rangle = \left[ E^{(1)}_\lambda \right]^2 \langle \mathbf 0_\lambda |\left(1 + \mathbf a_\lambda^\dag \mathbf a_\lambda\right) | \mathbf 0_\lambda \rangle =\left[\mathscr E^{(1)}_\lambda \right]^2 \end{aligned}
The fluctuations has an amplitude \Delta E:
\Delta E = \sqrt{\langle \mathbf E^2 \rangle - \langle \mathbf E \rangle^2 } = \sqrt{\langle \mathbf 0_\lambda | \mathbf{E}^2(\mathbf{r}) | \mathbf 0_\lambda \rangle - \| \langle \mathbf 0_\lambda | \mathbf{E}(\mathbf{r}) | \mathbf 0_\lambda \rangle \|^2} = \mathscr E^{(1)}_\lambda
Considering now \mathbf Q_\lambda and \mathbf P_\lambda, and calculating their fluctuations; starting from the average:
\begin{aligned} & \langle \mathbf 0_\lambda | \mathbf Q_\lambda | \mathbf 0_\lambda \rangle = \sqrt {\frac{\hbar}{2}} \langle \mathbf 0_\lambda | \left(\mathbf a_\lambda + \mathbf a_\lambda^\dag\right) | \mathbf 0_\lambda \rangle = 0 \\ & \langle \mathbf 0_\lambda | \mathbf P_\lambda | \mathbf 0_\lambda \rangle = i \sqrt {\frac{\hbar}{2}} \langle \mathbf 0_\lambda | \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right) | \mathbf 0_\lambda \rangle = 0 \end{aligned}
again because it there is either a factor \mathbf a_\lambda | \mathbf 0_\lambda \rangle = 0 or \langle \mathbf 0_\lambda | \mathbf a_\lambda^\dag = 0.
Their dispersion is:
\begin{aligned} \langle \mathbf 0_\lambda | \mathbf Q_\lambda^2 | \mathbf 0_\lambda \rangle & = \frac{\hbar}{2} \langle \mathbf 0_\lambda | \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag \right)^2 | \mathbf 0_\lambda \rangle \\ & = \frac{\hbar}{2} \langle \mathbf 0_\lambda | \left( \mathbf a_\lambda^2 - \mathbf a_\lambda \mathbf a_\lambda^\dag - \mathbf a_\lambda^\dag\mathbf a_\lambda + \left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 0_\lambda \rangle\\ & = \frac{\hbar}{2} \left[ \langle \left(\mathbf 0_\lambda |\mathbf a^2 \right) | \mathbf 0_\lambda \rangle + \langle \mathbf 0_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 0_\lambda \rangle + \left( \langle \mathbf 0_\lambda |\mathbf a_\lambda^\dag \right) \mathbf a_\lambda | \mathbf 0_\lambda \rangle + \left(\langle \mathbf 0_\lambda | \left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 0_\lambda \rangle \right] \\ & = \frac{\hbar}{2} \langle \mathbf 0_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 0_\lambda \rangle = \frac{\hbar}{2} \langle \mathbf 0_\lambda |\left(1 + \mathbf a_\lambda^\dag \mathbf a_\lambda\right) | \mathbf 0_\lambda \rangle = \frac{\hbar}{2} \\ \langle \mathbf 0_\lambda | \mathbf P_\lambda^2 | \mathbf 0_\lambda \rangle & = i^2 \frac{\hbar}{2} \langle \mathbf 0_\lambda | \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag \right)^2 | \mathbf 0_\lambda \rangle \\ & = -\frac{\hbar}{2} \langle \mathbf 0_\lambda | \left( \mathbf a_\lambda^2 - \mathbf a_\lambda \mathbf a_\lambda^\dag - \mathbf a_\lambda^\dag\mathbf a_\lambda + \left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 0_\lambda \rangle\\ & = -\frac{\hbar}{2} \left[ \langle \left(\mathbf 0_\lambda |\mathbf a^2 \right) | \mathbf 0_\lambda \rangle + \langle \mathbf 0_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 0_\lambda \rangle + \left( \langle \mathbf 0_\lambda |\mathbf a_\lambda^\dag \right) \mathbf a_\lambda | \mathbf 0_\lambda \rangle + \left(\langle \mathbf 0_\lambda | \left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 0_\lambda \rangle \right] \\ & = \frac{\hbar}{2} \langle \mathbf 0_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 0_\lambda \rangle = \frac{\hbar}{2} \langle \mathbf 0_\lambda |\left(1 + \mathbf a_\lambda^\dag \mathbf a_\lambda\right) | \mathbf 0_\lambda \rangle =\frac{\hbar}{2} \end{aligned}
The fluctuations has an amplitude \Delta Q and \Delta P:
\begin{aligned} \Delta Q_\lambda & = \sqrt{\langle \mathbf Q_\lambda^2 \rangle - \langle \mathbf Q_\lambda \rangle^2 } = \sqrt{\langle \mathbf 0_\lambda | \mathbf{Q_\lambda}^2 | \mathbf 0_\lambda \rangle - \| \langle \mathbf 0_\lambda | \mathbf{Q_\lambda} | \mathbf 0_\lambda \rangle \|^2} = \sqrt{\frac{\hbar}{2}} \\ \Delta P_\lambda & = \sqrt{\langle \mathbf P_\lambda^2 \rangle - \langle \mathbf P_\lambda \rangle^2 } = \sqrt{\langle \mathbf 0_\lambda | \mathbf{P_\lambda}^2 | \mathbf 0_\lambda \rangle - \| \langle \mathbf 0_\lambda | \mathbf{P_\lambda} | \mathbf 0_\lambda \rangle \|^2} = \sqrt{\frac{\hbar}{2}} \end{aligned}
Their product is:
\Delta Q_\lambda \Delta P_\lambda = \frac{\hbar}{2}
which is the minimum value allowed by Heisenberg uncertainty principle.
Photon
A photon is an elementary excitation of the quantized electromagnetic field; its property are related to the ones of the creation operator \mathbf a^\dag which create a photon from the vacuum state. If the creation operator involve only one momentum component, then the photon has a defined momentum, otherwise it is a linear superposition of component with different momenta. Similarly, if the creator operator has a single wavelength, it will have a definite energy, otherwise it will be a superposition of states with different energies.
Standing wave
Let’s consider a standing wave electromagnetic field confined in a cavity with reflecting mirrors:
\begin{aligned} & \mathbf A(x, t) = A(t) \mathbf e \sin( kx) \\ & \mathbf E(x, t) = E(t) \mathbf e \sin( kx) \\ & \mathbf B(x, t) = A(t) \mathbf k \times \mathbf e \cos( kx) \end{aligned}
where the wavevector \mathbf k is oriented along the x direction, and therefore the electromagnetic field lies in the yz plane.
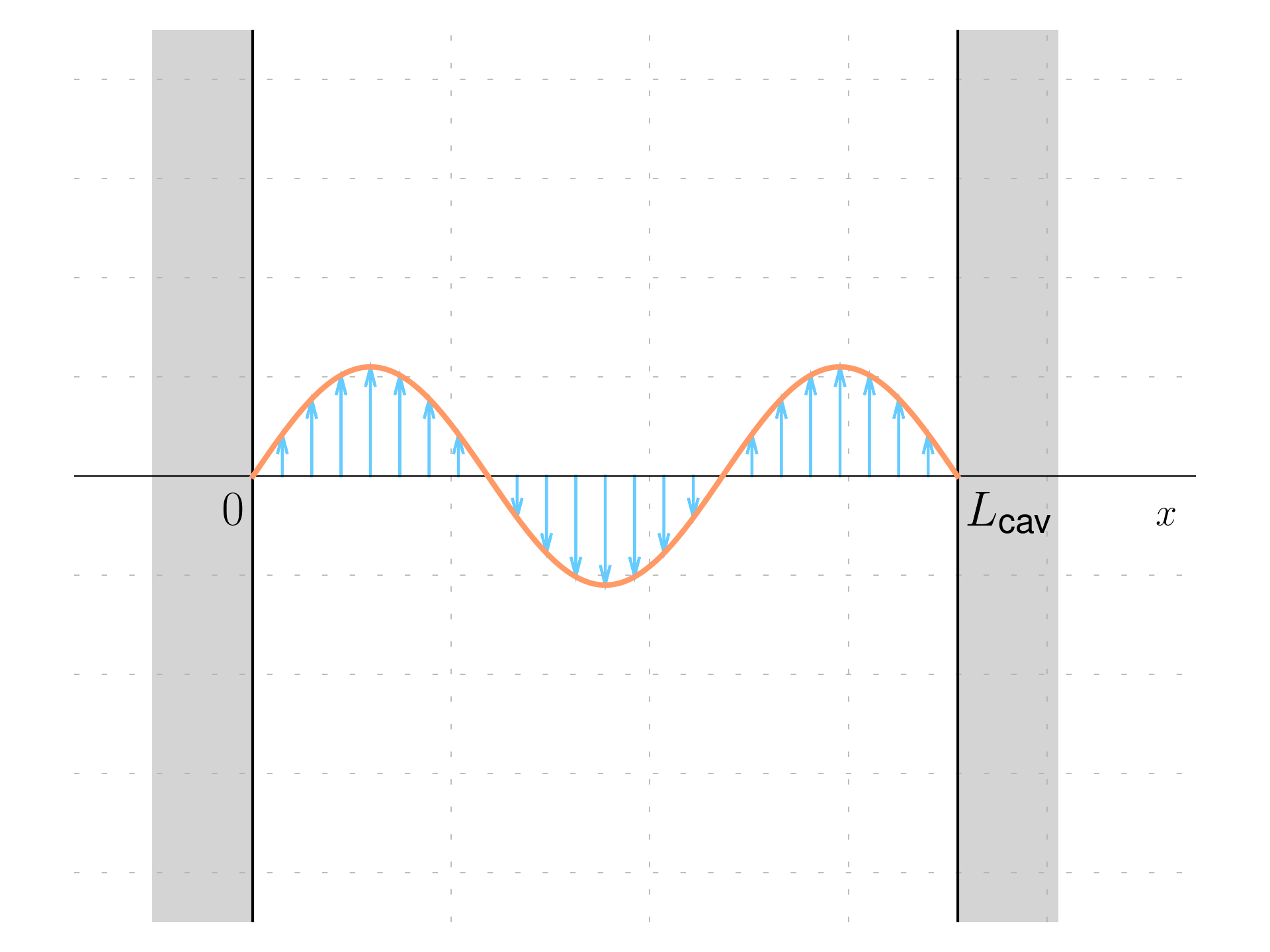
Since the cavity is reflecting, the electric field must be zero at the boundary and it is described by the boundary condition:
\mathbf E(x = 0) = \mathbf E(x = L) = 0
This forces the standing wave pattern in the box, because the only way to satisfy these boundary conditions with a non-zero field solution in the region 0 < x < L is if the field configuration has nodes (points of zero amplitude) at x = 0 and x = L. In this scenario, the electric field must be quantized. Only specific wavelengths corresponding to integer multiples of half-wavelengths fit into the box, and the condition \mathbf E(0) = \mathbf E(L) = 0 requires that kx be a multiple of \pi at x = L, which leads to the quantization condition:
kL = n\pi
where n is a positive integer, and k is the wavenumber. This further translates to:
k = \frac{n\pi}{L}
Using the equation \mathbf E(t) = -\frac{\partial \mathbf A(t)}{\partial t} and the Maxwell equations:
\begin{aligned} & \nabla ^2 \mathbf A(t) -\frac{1}{c^2}\frac{\partial^2 \mathbf A(t)}{\partial t^2} = 0 \\ & \frac{\partial \mathbf E(t)}{\partial t} = -\frac{\partial^2 \mathbf A(t)}{\partial t^2} = -c^2 \nabla ^2 \mathbf A(t) \end{aligned}
Since:
\begin{aligned} & \mathbf A(x, t) = A(t) \mathbf e \sin( kx) \\ & \nabla ^2 \mathbf A(t) = -k^2 A(t) \mathbf e \sin( kx) \end{aligned}
substituting and defining an angular frequency \omega \equiv ck:
\frac{\partial \mathbf E(t)}{\partial t} = -c^2 \nabla ^2 \mathbf A(t) = c^2 k^2\mathbf A(t) = \omega^2 \mathbf A(t)
Let’s define the dimensionless parameter \alpha(t) as:
\alpha(t) = \frac{1}{2 \mathscr E^{(1)}_{sw}}(\omega \mathbf A(t) - i\mathbf E(t))
where \mathscr E^{(1)}_{sw} is a normalization factor which has the dimensions of an electric field. Taking the time derivative:
\begin{aligned} \frac{\mathrm \alpha(t)}{\mathrm dt} & = \frac{\mathrm d}{\mathrm dt}\left[\frac{1}{2 \mathscr E^{(1)}_{sw}}(\omega \mathbf A(t) - i\mathbf E(t)) \right] = \frac{1}{2 \mathscr E^{(1)}_{sw}} \left(\omega \frac{\mathrm d\mathbf A(t)}{\mathrm dt} - i\frac{\mathrm d\mathbf E(t)}{\mathrm dt} \right) \\ & = \frac{1}{2 \mathscr E^{(1)}_{sw}} \left(-\omega \mathbf E(t) - i\omega^2 \mathbf A(t)\right) = \frac{-i\omega}{2 \mathscr E^{(1)}_{sw}} \left(-i \mathbf E(t) + \omega \mathbf A(t)\right) \\ & = i\omega \alpha(t) \end{aligned}
The energy of the mode can be written as:
\mathcal H = \frac{\varepsilon_0}{2} \int_{V_{\text{cav}}}\left( \mathbf E^2 + c^2 \mathbf B^2\right) \mathrm d\mathbf r^3
where V_{\text{cav}} = L_{\text{cav}} L^2 is the quantization volume for a planar cavity of length L_{\text{cav}}. The length L is the size of the quantization volume in the transverse direction with respect to the mode axis.
The magnitude square of the magnetic field is:
(A(t) \mathbf k \times \mathbf e \cos( kx))^2 = A(t)^2 k^2 \cos^2( kx)
as:
|\mathbf{k} \times \mathbf{e}| = |\mathbf{k}| |\mathbf{e}| \sin(90^\circ) = |\mathbf{k}|
Substituting the values:
\begin{aligned} \mathcal H & = \frac{\varepsilon_0}{2} \int_{V_{\text{cav}}}\left( \mathbf E(t)^2 + c^2 \mathbf B^2\right) \mathrm d\mathbf r^3 = \int_{V_{\text{cav}}} \left(E^2 \sin^2( kx) + c^2 A(t)^2 k^2 \cos^2( kx) \right) \mathrm d\mathbf r^3 \\ & =\frac{\varepsilon_0}{2}\left[ E(t)^2 \int_{V_{\text{cav}}} \sin^2( kx)\mathrm d\mathbf r^3 + \omega^2 A(t)^2 \int_{V_{\text{cav}}} \cos^2( kx) \mathrm d\mathbf r^3 \right]\\ & = \frac{\varepsilon_0}{2}\left[E(t)^2 \int_{S_{\text{orth}}} \mathrm dy \mathrm dz \int_{L_{\text{cav}}} \sin^2( kx)\mathrm dx + \omega^2 A(t)^2 \int_{S_{\text{orth}}} \mathrm dy \mathrm dz \int_{L_{\text{cav}}} \cos^2( kx) \mathrm dx \right]\\ & = \frac{\varepsilon_0}{2}\left[E(t)^2 L^2 \int_{L_{\text{cav}}} \sin^2( kx)\mathrm dx + \omega^2 A(t)^2 L^2 \int_{L_{\text{cav}}} \cos^2( kx) \mathrm dx \right]\\ & = \frac{\varepsilon_0}{2}\left[ E(t)^2 L^2 \frac{L_{\text{cav}}}{2} + \omega^2 A(t)^2 L^2 \frac{L_{\text{cav}}}{2} \right] = \frac{\varepsilon_0V_{\text{cav}}}{4}\left(E(t)^2 +\omega^2 A(t)^2 \right) \end{aligned}
The integral as been evaluated as:
\begin{aligned} & \int_{L_{\text{cav}}} \sin^2( kx)\mathrm d x = \frac{L}{2} - \frac{\sin(2n\pi L)}{4n\pi} \\ & \int_{L_{\text{cav}}} \cos^2( kx) \mathrm dx = \frac{L}{2} + \frac{\sin(2n\pi L)}{4n\pi} \end{aligned}
which evaluate to \frac{L}{2} as k = \frac{n\pi}{L}.
Using the definition of \alpha(t):
\left| \alpha(t) \right|^2 = \frac{1}{4 \left[\mathscr E^{(1)}_{sw}\right]^2}(\omega^2 A(t)^2 + E(t)^2)
Choosing:
\mathscr E^{(1)}_{sw} = \sqrt{\frac{\hbar \omega}{\varepsilon_0 V_{\text{cav}}}}
It can be written as:
\mathcal H = \frac{\varepsilon_0V_{\text{cav}}}{4}\left(E(t)^2 +\omega^2 A(t)^2 \right) = \varepsilon_0V_{\text{cav}} \left[\mathscr E^{(1)}_{sw}\right]^2 \left| \alpha(t) \right|^2 = \hbar \omega \left| \alpha(t) \right|^2
Canonical conjugate variables
From the definition of \alpha(t) is it possible to write the field potential and the electric field as function of \alpha(t):
\begin{aligned} & \alpha(t) = \frac{1}{2 \mathscr E^{(1)}_{sw}}(\omega \mathbf A(t) - i\mathbf E(t)) \\ & \bar \alpha(t) = \frac{1}{2 \mathscr E^{(1)}_{sw}}(\omega \mathbf A(t) + i\mathbf E(t)) \\ & \alpha(t) + \bar \alpha(t) = \frac{1}{\mathscr E^{(1)}_{sw}} \omega \mathbf A(t) \\ & \alpha(t) - \bar \alpha(t) = -\frac{i}{\mathscr E^{(1)}_{sw}} \mathbf E(t) \end{aligned}
therefore:
\begin{aligned} & \mathbf A(x, t) = A(t) \mathbf e \sin( kx) = \frac{\mathscr E^{(1)}_{sw}}{\omega}\left(\alpha(t) + \bar \alpha(t) \right) \mathbf e \sin( kx) \\ & \mathbf E(x, t) = E(t) \mathbf e \sin( kx) = -i\mathscr E^{(1)}_{sw}\left(\alpha(t) - \bar \alpha(t) \right) \mathbf e \sin( kx) \end{aligned}
By analogy of a plain wave we introduce the real and imaginary part of \alpha (the factor is to simplify formulas at a later stage):
\begin{aligned} \alpha_\lambda(t) & = \frac{1}{\sqrt {2\hbar}}\left(Q + iP\right) \\ Q & = \Re{(\alpha_\lambda)} = \sqrt{\frac{\hbar}{2}}\left(\alpha_\lambda(t) + \bar \alpha_\lambda(t)\right) = \sqrt{\frac{\hbar}{2}} \frac{1}{\mathscr E^{(1)}_{sw}} \omega \mathbf A(t) \\ & = \sqrt{\frac{\hbar}{2}} \sqrt{\frac{\varepsilon_0 V_{\text{cav}}}{\hbar \omega}} \omega \mathbf A(t) = \sqrt{\frac{\varepsilon_0 \omega V_{\text{cav}}}{2}} \mathbf A(t) \\ P & = \Im{(\alpha_\lambda)} = -\sqrt{\frac{\hbar}{2}}\left(\alpha_\lambda(t) - \bar \alpha_\lambda(t)\right) = -\sqrt{\frac{\hbar}{2}} \frac{1}{\mathscr E^{(1)}_{sw}} \mathbf E(t)\\ & = -\sqrt{\frac{\hbar}{2}} \sqrt{\frac{\varepsilon_0 V_{\text{cav}}}{\hbar \omega}} \mathbf E(t) = -\sqrt{\frac{\varepsilon_0 V_{\text{cav}}}{2 \omega}} \mathbf E(t) \end{aligned}
The Hamiltonian becomes:
\begin{aligned} \mathcal H & = \frac{\varepsilon_0V_{\text{cav}}}{4}\left(E(t)^2 +\omega^2 A(t)^2 \right) =\frac{\varepsilon_0V_{\text{cav}}}{4}\left(\frac{2 \omega}{\varepsilon_0 V_{\text{cav}}} P^2 +\omega^2 \frac{2}{\omega \varepsilon_0 V_{\text{cav}}} Q^2 \right) \\ & = \frac{\omega}{2}\left(Q^2 + P^2\right) \end{aligned}
which is again an harmonic oscillator, and it is now possible to perform the canonical quantization of the field.
Field quantization
It is possible to apply the canonical quantization, defining two operator and postulating their commutator:
\begin{aligned} & \mathbf Q = \sqrt{\frac{\hbar}{2}} \frac{1}{\mathscr E^{(1)}_{sw}} \omega \mathbf A(t)\\ & \mathbf P = \sqrt{\frac{\hbar}{2}} \frac{1}{\mathscr E^{(1)}_{sw}} \mathbf E(t) \\ & [ \mathbf Q, \mathbf P] = i\hbar \end{aligned}
The quantized Hamiltonian becomes:
\mathbf H = \frac{\omega}{2}\left(\mathbf Q^2 + \mathbf P^2\right)
This is an Harmonic oscillator, we then introduce the equivalent quantization of \alpha and \bar \alpha:
\begin{aligned} & \mathbf b = \frac{1}{\sqrt {2\hbar}}\left(\mathbf Q + i\mathbf P\right) = \frac{1}{2 \mathscr{E}^{(1)}_{sw}} \left( \omega \mathbf{A}(t) + i\mathbf{E}(t) \right) \\ & \mathbf b^\dag = \frac{1}{\sqrt {2\hbar}}\left(\mathbf Q - i\mathbf P\right) = \frac{1}{2 \mathscr{E}^{(1)}_{sw}} \left( \omega \mathbf{A}(t) - i\mathbf{E}(t) \right) \end{aligned}
Their commutator is:
[\mathbf b, \mathbf b^\dag] = 1
retrieving \mathbf Q and \mathbf P from the definitions, and use the commutator relations, give the Hamiltonian:
\mathbf H = \hbar \omega\left(\mathbf b \mathbf b^\dag + \frac{1}{2}\right)
It is possible to express the potential and the electric field based on these operators:
\begin{aligned} & \mathbf b + \mathbf b^\dag = \frac{1}{2 \mathscr{E}^{(1)}_{sw}} \left( \omega \mathbf{A}(t) + i\mathbf{E}(t) \right) + \frac{1}{2 \mathscr{E}^{(1)}_{sw}} \left( \omega \mathbf{A}(t) - i\mathbf{E}(t) \right) = \frac{\omega \mathbf{A}(t)}{\mathscr{E}^{(1)}_{sw}} \\ & \mathbf b - \mathbf b^\dag =\frac{1}{2 \mathscr{E}^{(1)}_{sw}} \left( \omega \mathbf{A}(t) + i\mathbf{E}(t) \right) - \frac{1}{2 \mathscr{E}^{(1)}_{sw}} \left( \omega \mathbf{A}(t) - i\mathbf{E}(t) \right) = \frac{i\mathbf{E}(t)}{\mathscr{E}^{(1)}_{sw}} \end{aligned}
and therefore:
\begin{aligned} & \mathbf A(x, t) = A(t) \mathbf e \sin( kx) = \frac{\mathscr E^{(1)}_{sw}}{\omega}\left(\mathbf b + \mathbf b^\dag \right) \mathbf e \sin( kx) \\ & \mathbf E(x, t) = E(t) \mathbf e \sin( kx) = i\mathscr E^{(1)}_{sw}\left(\mathbf b - \mathbf b^\dag \right) \mathbf e \sin( kx) \end{aligned}
Traveling waves superposition
A traveling wave electric field operators with wavevector \mathbf{k} and polarization \mathbf e along the x axis is defined by
\mathbf E_{k,e}(x) = i \mathscr{E}^{(1)}_{\mathbf{k}} \mathbf e \left( \mathbf a_{k,e} e^{i k x} - \mathbf a^{\dagger}_{k,e} e^{-i k x} \right)
with
\mathscr{E}^{(1)}_{\mathbf{k}} = \sqrt{\frac{\hbar \omega}{2 \varepsilon_0 V_{\text{cav}}}}
Given the traveling wave electric field operators \mathbf E_{k,e}(x) and \mathbf E_{-k,e}(x), the superposition of two counter-propagating waves can be expressed as:
\begin{aligned} \mathbf E(x) = & \mathbf E_{k,e}(x) + \mathbf E_{-k,e}(x) \\ =& \frac{i}{\sqrt 2} \mathscr{E}_{\mathbf{k}}^{(1)} \mathbf e \left( \mathbf a_{k,e} e^{i kx} - \mathbf a_{k,e}^\dagger e^{-i kx} \right) \\ & + \frac{i}{\sqrt 2} \mathscr{E}_{\mathbf{k}}^{(1)} \mathbf e \left( \mathbf a_{-k,e} e^{-i kx} - \mathbf a_{-k,e}^\dagger e^{i kx} \right) \end{aligned}
where the factor \frac{1}{\sqrt 2} is for normalization. Combining these:
\begin{aligned} \mathbf E(x) = & \mathbf E_{k,e}(x) + \mathbf E_{-k,e}(x) = \frac{i}{\sqrt 2} \mathscr{E}_{\mathbf{k}}^{(1)} \mathbf e \left[ \left( \mathbf a_{k,e} e^{i kx} - \mathbf a_{k,e}^\dagger e^{-i kx} \right) + \left( \mathbf a_{-k,e} e^{-i kx} - \mathbf a_{-k,e}^\dagger e^{-i kx} \right) \right]\\ = & \frac{i}{\sqrt 2} \mathscr{E}_{\mathbf{k}}^{(1)} \mathbf e \left[ \mathbf a_{k,e} e^{i kx} + \mathbf a_{-k,e} e^{-i kx} - \mathbf a_{k,e}^\dagger e^{-i kx} - \mathbf a_{-k,e}^\dagger e^{i kx} \right]\\ = & \frac{i}{\sqrt 2} \mathscr{E}_{\mathbf{k}}^{(1)} \mathbf e \left[ \left( \mathbf a_{k,e} (\cos(kx) + i \sin(kx)) + \mathbf a_{-k,e} (\cos(kx) - i \sin(kx)) \right) \right. \\ &\left. - \mathbf a_{k,e}^\dagger (\cos(kx) - i \sin(kx)) - \mathbf a_{-k,e}^\dagger (\cos(kx) + i \sin(kx)) \right] \\ = & \frac{i}{\sqrt 2} \mathscr{E}_{\mathbf{k}}^{(1)} \mathbf e \left[ (\mathbf a_{k,e} + \mathbf a_{-k,e} - \mathbf a_{k,e}^\dagger - \mathbf a_{-k,e}^\dagger) \cos(kx)\right.\\ & \left. + i (\mathbf a_{k,e} - \mathbf a_{-k,e} + \mathbf a_{k,e}^\dagger - \mathbf a_{-k,e}^\dagger) \sin(kx) \right]\\ = & \frac{\mathscr{E}_{\mathbf{k}}^{(1)}}{\sqrt 2} \mathbf e \left[ ( \mathbf a_{k,e}^\dagger - \mathbf a_{-k,e}^\dagger - \mathbf a_{k,e} + \mathbf a_{-k,e}) \sin(kx) \right.\\ & \left. + i (\mathbf a_{k,e} + \mathbf a_{-k,e} - \mathbf a_{k,e}^\dagger - \mathbf a_{-k,e}^\dagger) \cos(kx) \right] \end{aligned}
Now since this applies to a cavity, to satisfy the condition where the cosine term is zero, the relation between the operators \mathbf a_{k,e} and \mathbf a_{-k,e} must be such that the coefficient of \cos(kx) becomes zero:
\mathbf a_{k,e} + \mathbf a_{-k,e} - \mathbf a_{k,e}^\dagger - \mathbf a_{-k,e}^\dagger = 0
This implies:
-(\mathbf a_{-k,e}^\dagger - \mathbf a_{-k,e}) = \mathbf a_{k,e}^\dagger - \mathbf a_{k,e}
The superposition of the electric field operators \mathbf E_{k,e}(z) and \mathbf E_{-k,e}(z) becomes:
\begin{aligned} \mathbf E(x) & = \mathbf E_{k,e}(z) + \mathbf E_{-k,e}(z) = \frac{\mathscr{E}_{\mathbf{k}}^{(1)}}{\sqrt 2} \mathbf e \left[ ( \mathbf a_{k,e}^\dagger - \mathbf a_{-k,e}^\dagger - \mathbf a_{k,e} + \mathbf a_{-k,e}) \sin(kx) \right] \\ & = \frac{\mathscr{E}_{\mathbf{k}}^{(1)}}{\sqrt 2} \mathbf e \left[ ( \mathbf a_{k,e}^\dagger - \mathbf a_{k,e} - (\mathbf a_{-k,e}^\dagger - \mathbf a_{-k,e})) \sin(kx) \right] = \sqrt 2 \mathscr{E}_{\mathbf{k}}^{(1)} \mathbf e (\mathbf a_{k,e}^\dagger - \mathbf a_{k,e}) \sin(kx) \end{aligned}