One Photon State Single Mode
Semi-classical model of optics
In the semi-classical model, the light can be considered modes of the electromagnetic field; with the results detailed here it can be written, considering different modes, as:
\begin{aligned} \mathbf{E}(\mathbf{r}, t) & = \sum_\lambda E_\lambda(t) \mathbf{e}_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} + \text{c.c.} = \sum_\lambda i \mathcal E_\lambda \alpha_\lambda(t) \mathbf{e}_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} + \text{c.c.}\\ & = \sum_\lambda \mathcal E_\lambda(0) \mathbf{e}_\lambda e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} -\omega_\lambda t)} + \text{c.c.} \\ & = \mathbf{E}^{(+)}(\mathbf{r}, t) + \mathbf{E}^{(-)}(\mathbf{r}, t) \end{aligned}
\mathbf{E}^{+} is called the positive part of the electric field amplitude, although the frequency comes with a minus sign.
In contrast to radiation, the electrons in motion inside matter are quantized, i.e. they can take only specific level of energy.

Above the ionization threshold, the electron is free and no longer bounded around the atom; the representation using circular orbits is not correct, but sufficiently good to give the idea about the behavior.
In the semi-classical model, the interaction is between the classical electric field with the quantized atom and could be described by an interaction Hamiltonian involving an observable associated with the electrons:
\mathbf H = -\mathbf D \cdot \mathbf E(\mathbf r, t)
\mathbf D is the quantum electric dipole and \mathbf E(\mathbf r, t) is the classical electric field.
Photoelectric effect
The semi-classical model allows the description of the photoelectric effect, which is the ejection of electrons from matter illuminated by incident radiation under the effect of an frequency \omega higher than a specific threshold.
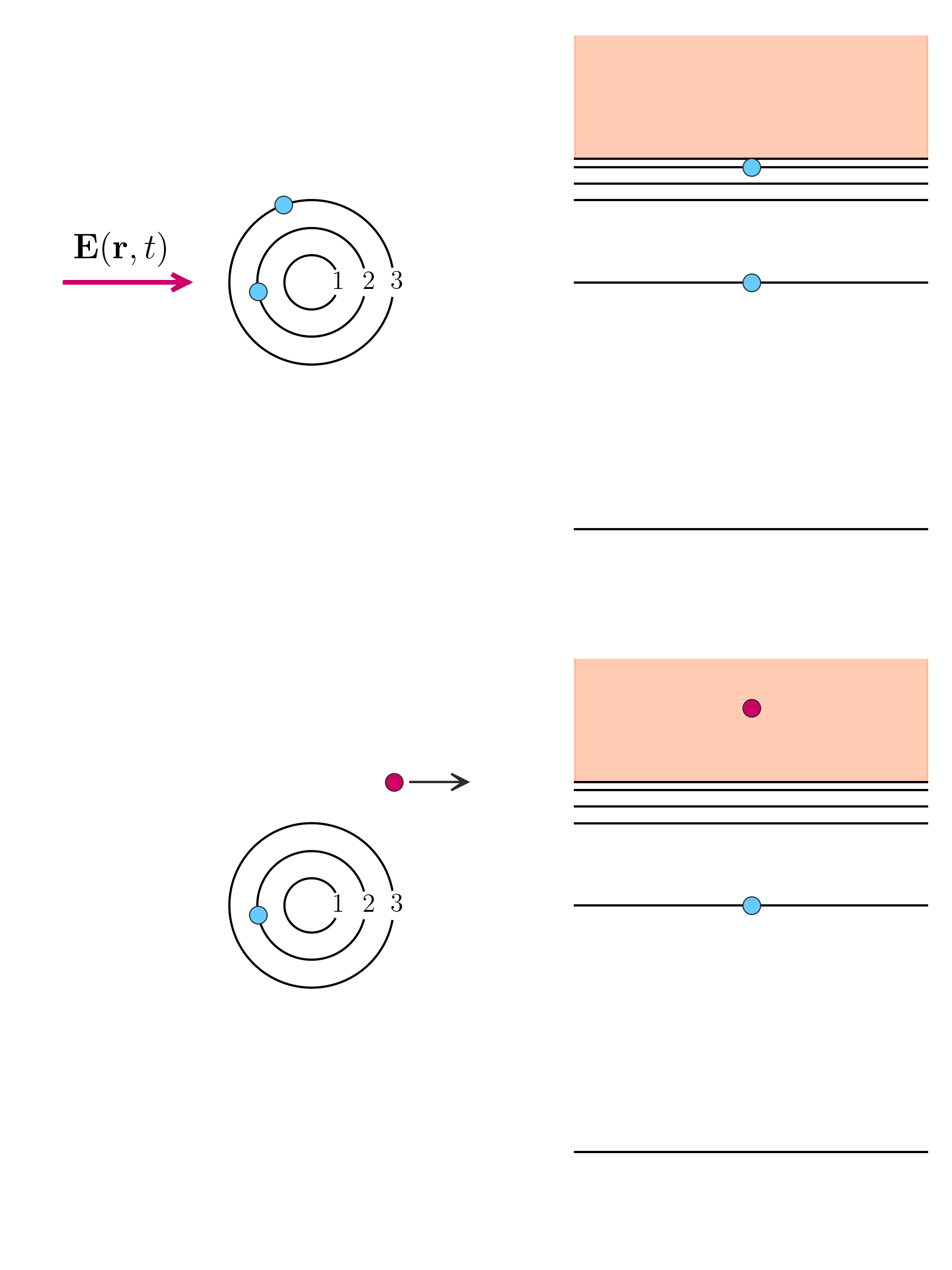
When it is associated with an electron multiplier, the photoelectric effect allows the photon counting regime, where a primary electron is released and through a series of dynodes is amplified several times in order to produce sufficient voltage that can be measured.
The probability for an extraction of an electron extraction in a surface \mathrm dS around \mathbf r for a time \mathrm dt is:
\mathrm dP(\mathbf r,t) = w^{(1)}(\mathbf r,t)\,\mathrm dS \,\mathrm dt = s\left|\mathbf E^{(+)}(\mathbf r,t)\right|^2\,\mathrm dS\,\mathrm dt
The proportional coefficient s is called the sensitivity and depends from the frequency. the index (1) is because the interest is of the event where a single electron is extracted from the photocathode.
An interesting test for quantum optics is the double detection probability, which is the probability of detecting two photons by two detectors:
\mathrm dP^2(\mathbf r_1,t,\mathbf r_2,t) = w^{(2)}(\mathbf r_1,t,\mathbf r_2,t)\,\mathrm dS_1 \,\mathrm dt\,\mathrm dS_2 \,\mathrm dt
This experiments was one of the fundamental for the develop quantum optics; in the semi-classical model it the probability is just:
\mathrm dP^2(\mathbf r_1,t,\mathbf r_2,t) = s^2 \left|\mathbf E^{(+)}(\mathbf r_1,t)\right|^2 \left|\mathbf E^{(+)}(\mathbf r_2,t)\right|^2\,\mathrm dS_1 \,\mathrm dt\,\mathrm dS_2 \,\mathrm dt
It is therefore just the product of the single detection rate w^{(1)}, since the electron emission are independent event once the electric field is set.
One Photon State Single Mode
In the formalism of the light quantization (here), the single mode is the case where n_\lambda=1:
| \mathbf 1_\lambda \rangle = | 0, \dots n_\lambda = 1 , \dots, 0 \rangle
It means that measuring with a perfect detector it will find exactly one photon.
The average of the observable of the electric field is zero:
\begin{aligned} \langle \mathbf 1_\lambda | \mathbf E(\mathbf r) | \mathbf 1_\lambda \rangle = & \langle \mathbf 1_\lambda | i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right)| \mathbf 1_\lambda \rangle \\ = & i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda\left[ e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} \mathbf 1_\lambda |\left( a_\lambda | \mathbf 1_\lambda \rangle \right) - e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \left( \langle \mathbf 1_\lambda |\mathbf a_\lambda^\dag \right) | \mathbf 1_\lambda \rangle \right] \\ = & i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda\left[ e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} \langle \mathbf 1_\lambda | \mathbf 0_\lambda \rangle - e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \langle \mathbf 0_\lambda | \mathbf 1_\lambda \rangle \right] = 0 \end{aligned}
since | \mathbf 0 \rangle and |\mathbf 1 \rangle are orthogonal. The average of other observable (like \mathbf Q or \mathbf P) are also zero for the same reason.
As for the case for the value, it does not means that there is no variation; evaluating the square of the electric field:
\begin{aligned} \langle \mathbf 1_\lambda | \mathbf{E}^2(\mathbf{r}) | \mathbf 1_\lambda \rangle & = i^2\left[\mathscr E^{(1)}_\lambda \right]^2 \langle \mathbf 1_\lambda | \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right)^2 | \mathbf 1_\lambda \rangle \\ & = -\left[\mathscr E^{(1)}_\lambda \right]^2 \langle \mathbf 1_\lambda | \left(e^{2i\mathbf{k}_\lambda \cdot \mathbf{r}} \mathbf a_\lambda^2 - \mathbf a_\lambda \mathbf a_\lambda^\dag - \mathbf a_\lambda^\dag\mathbf a_\lambda + e^{-2i\mathbf{k}_\lambda \cdot \mathbf{r}}\left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 1_\lambda \rangle\\ & = \left[\mathscr E^{(1)}_\lambda \right]^2 \left[ -e^{2i\mathbf{k}_\lambda \cdot \mathbf{r}}\langle \mathbf 1_\lambda | \left(\mathbf a^2 | \mathbf 1_\lambda \right) \rangle + \langle \mathbf 1_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 1_\lambda \rangle + \langle \mathbf 1_\lambda |\mathbf a_\lambda^\dag \mathbf a_\lambda | \mathbf 1_\lambda \rangle -e^{-2i\mathbf{k}_\lambda \cdot \mathbf{r}} \left(\langle \mathbf 1_\lambda | \left(\mathbf a_\lambda^\dag\right)^2 \right) | \mathbf 1_\lambda \rangle \right] \\ & = \left[\mathscr E^{(1)}_\lambda \right]^2 \left[ -e^{2i\mathbf{k}_\lambda \cdot \mathbf{r}}\langle \mathbf 1_\lambda \left(|\mathbf a | \mathbf 0_\lambda \rangle\right) + \langle \mathbf 1_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 1_\lambda \rangle + \langle \mathbf 1_\lambda |\mathbf a_\lambda^\dag \mathbf a_\lambda | \mathbf 1_\lambda \rangle -e^{-2i\mathbf{k}_\lambda \cdot \mathbf{r}} \left(\langle \mathbf 0_\lambda | \left(\mathbf a_\lambda^\dag\right) \right) | \mathbf 1_\lambda \rangle \right] \\ & = \left[\mathscr E^{(1)}_\lambda \right]^2 \left[ \langle \mathbf 1_\lambda |\mathbf a_\lambda \mathbf a_\lambda^\dag | \mathbf 1_\lambda \rangle + \langle \mathbf 1_\lambda |\mathbf a_\lambda^\dag \mathbf a_\lambda | \mathbf 1_\lambda \rangle \right] = \left[\mathscr E^{(1)}_\lambda \right]^2 \left[ \langle \mathbf 1_\lambda | 1 + \mathbf a_\lambda^\dag \mathbf a_\lambda | \mathbf 1_\lambda \rangle + \langle \mathbf 1_\lambda |\mathbf a_\lambda^\dag \mathbf a_\lambda | \mathbf 1_\lambda \rangle \right] \\ & = \left[\mathscr E^{(1)}_\lambda \right]^2 \left[ 1 \langle \mathbf 1_\lambda | \mathbf 1_\lambda \rangle + 2 \langle \mathbf 1_\lambda |\mathbf a_\lambda^\dag \mathbf a_\lambda | \mathbf 1_\lambda \rangle \right] = \left[\mathscr E^{(1)}_\lambda \right]^2 \left[ 1 + 2 \langle \mathbf 0_\lambda | \mathbf 0_\lambda \rangle \right] = 3\left[\mathscr E^{(1)}_\lambda \right]^2 \end{aligned}
The fluctuations has an amplitude \Delta E:
\Delta E = \sqrt{\langle \mathbf E^2 \rangle - \langle \mathbf E \rangle^2 } = \sqrt{\langle \mathbf 1_\lambda | \mathbf{E}^2(\mathbf{r}) | \mathbf 1_\lambda \rangle - \| \langle \mathbf 1_\lambda | \mathbf{E}(\mathbf{r}) | \mathbf 1_\lambda \rangle \|^2} = \sqrt 3 \mathscr E^{(1)}_\lambda
Similar computations will give:
\begin{aligned} & \langle \mathbf 0_\lambda | \mathbf Q_\lambda | \mathbf 0_\lambda \rangle = 0 \\ & \langle \mathbf 0_\lambda | \mathbf P_\lambda | \mathbf 0_\lambda \rangle = 0 \\ & \langle \mathbf 0_\lambda | \left(\mathbf Q_\lambda\right)^2 | \mathbf 0_\lambda \rangle = 3\frac{\hbar}{2} \\ & \langle \mathbf 0_\lambda | \left(\mathbf P_\lambda\right)^2 | \mathbf 0_\lambda \rangle = 3\frac{\hbar}{2} \\ & \Delta \mathbf Q_\lambda = \sqrt 3 \sqrt {\frac{\hbar}{2}} \\ & \Delta \mathbf P_\lambda = \sqrt 3 \sqrt {\frac{\hbar}{2}} \end{aligned}
Their product is:
\Delta Q_\lambda \Delta P_\lambda = 3\frac{\hbar}{2}
which is three time greater than minimum value allowed by Heisenberg uncertainty principle; this is not a minimum dispersion state.
The way \mathscr E^{(1)}_\lambda appears to depends from the volume of quantization:
\mathscr E^{(1)}_\lambda = \sqrt{\frac{\hbar \omega_\lambda}{2\epsilon_0 V_\lambda}}
while experiments give a precise value which does not depend from the volume. The solution of this apparent paradox is that one-photon states come in wavepackets of finite extension. It can be studied with an approximated model, considering a traveling plane wave that has a limited transverse section S_\lambda (for example considering all the light emitted by an atom which is placed as the focus of a parabolic mirror. Providing that S_\lambda \gg \lambda^2 the approximation to consider the beam with constant section is relatively correct.
The duration is a finite time T_\lambda which is large compared to the period of oscillation, T_\lambda \gg \frac{2\pi}{\omega_\lambda}, then the length of the wavepacket is L = c\,T_\lambda.
The quantization volume is then:
V_\lambda = S_\lambda\,c\,T_\lambda
and in this volume the number of photons is well defined and can be measured with a detector D integrating the signal over a period of time bigger that T_\lambda.
Photo-detection signals
The expression of the photodetection signals can be derived using the expression of the Hamiltonian:
\mathbf H = -\mathbf D \cdot \mathbf E(\mathbf r)
\mathbf D is a quantized detector and \mathbf E(\mathbf r) is the quantized electric field. It appears identical to the semi-classical Hamiltonian, but it is very different in reality; both quantity are quantized, but the electric field it is now an operator; the physical result (an atom is excited and an electron escape) it is exactly the same, but the describing mathematics is quite different.
Using this approach, the probability formula is the same, but the definition of the single detection rate w^{(1)} is different:
\begin{aligned} \mathrm dP(\mathbf r,t) & = w^{(1)}(\mathbf r,t)\,\mathrm dS \,\mathrm dt = s\langle \psi | \mathbf{E}^{(-)}(\mathbf{r}) \mathbf{E}^{(+)}(\mathbf{r}) | \psi \rangle \,\mathrm dS\,\mathrm dt \\ & = s\langle \psi | \left(\sum_\lambda -i \mathscr E^{(1)}_\lambda \mathbf{e}_\lambda \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \sum_\lambda i \mathscr E^{(1)}_\lambda \mathbf{e}_\lambda \mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}}\right) | \psi \rangle \,\mathrm dS\,\mathrm dt \\ & = s\left\| \mathbf{E}^{(+)}(\mathbf{r}) | \psi \rangle\right\|^2 \,\mathrm dS\,\mathrm dt \end{aligned}
For a single photon state w^{(1)} is:
\begin{aligned} w^{(1)}(\mathbf r,t) & = s\langle \psi | \mathbf{E}^{(-)}(\mathbf{r}) \mathbf{E}^{(+)}(\mathbf{r}) | \psi \rangle \\ & = s\langle \psi | i^2 \left(\mathbf{e}_\lambda \cdot \mathbf{e}_\lambda\right) \left[\mathscr E^{(1)}_\lambda\right]^2 \left(-\mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}}\right) | \psi \rangle \\ & = s \left[\mathscr E^{(1)}_\lambda\right]^2 \langle \mathbf 1| e^{i\omega t} \left(\mathbf a_\lambda^\dag \mathbf a_\lambda e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} e^{i\mathbf{k}_\lambda \cdot \mathbf{r}}\right) | \mathbf 1 \rangle e^{-i\omega t} \\ & = s\left[\mathscr E^{(1)}_\lambda\right]^2 \langle \mathbf 1| \left(\mathbf a_\lambda^\dag \mathbf a_\lambda \right) | \mathbf 1 \rangle e^{i\omega t} e^{-i\omega t} \\ & = s\left[\mathscr E^{(1)}_\lambda\right]^2 \langle \mathbf 1| \left(\mathbf a_\lambda^\dag \mathbf a_\lambda \right) | \mathbf 1 \rangle = s\left[\mathscr E^{(1)}_\lambda\right]^2 \end{aligned}
For a single detection the formula is the quantum analog of the semi-classical expression. Using the definition of \mathscr E^{(1)}_\lambda and the quantization volume:
w^{(1)}(\mathbf r,t) = s\left[\mathscr E^{(1)}_\lambda\right]^2 = s\frac{\hbar \omega_\lambda}{2\epsilon_0 V_\lambda} = s \frac{\hbar \omega_\lambda}{2\epsilon_0 S_\lambda\,c\,T_\lambda}
Integrating the probability over the area S:
\frac{\mathrm dP}{\mathrm dt} = \iint_{S_\lambda} \mathrm dS w^{(1)}(\mathbf r,t) = s \frac{\hbar \omega_\lambda}{2\epsilon_0 c\,T_\lambda}
Finally integrating over time:
P = \int_{T_\lambda} \frac{\mathrm dP}{\mathrm dt} \mathrm dt = s \frac{\hbar \omega_\lambda}{2\epsilon_0 c\,T_\lambda} \int \mathrm dt = s \frac{\hbar \omega_\lambda}{2\epsilon_0 c}
Since for a perfect detector P = 1, it gives the sensitivity s as:
s_{0} = \frac{2\epsilon_0 c}{\hbar \omega_\lambda}
Real detectors have the sensitivity smaller then one by a factor \eta called quantum efficiency:
\eta = \frac{s}{s_0} \le 1
Then w^{(1)}(\mathbf r,t) has a particularly simple expression:
w^{(1)}(\mathbf r,t) = \eta \frac{1}{S_\lambda T_\lambda}
When considering the double detection the results are different from the semi-classical approach:
\begin{aligned} \mathrm dP^2(\mathbf r_1,t,\mathbf r_2,t) & = w^{(2)}(\mathbf r_1,t,\mathbf r_2,t)\,\mathrm dS_1 \,\mathrm dt\,\mathrm dS_2 \,\mathrm dt \\ & = s^2\langle \psi | \mathbf{E}^{(-)}(\mathbf{r_1}) \mathbf{E}^{(-)}(\mathbf{r_2}) \mathbf{E}^{(+)}(\mathbf{r_2}) \mathbf{E}^{(+)}(\mathbf{r_1}) | \psi \rangle \,\mathrm dS_1 \,\mathrm dt\,\mathrm dS_2 \,\mathrm dt \\ & = s^2\left\| \mathbf{E}^{(+)}(\mathbf{r_2}) \mathbf{E}^{(+)}(\mathbf{r_1})| \psi \rangle\right\|^2 \,\mathrm dS_1 \,\mathrm dt\,\mathrm dS_2 \,\mathrm dt \end{aligned}
It is evident already that differently from the classical case, w^{(2)} is not just the product of the two w^{(1)}:
w^{(2)}(\mathbf r_1,t,\mathbf r_2,t) \neq w^{(2)}(\mathbf r_1,t)w^{(2)}(\mathbf r_2,t)
The reason is that the first photodetector destroy a photon and therefore changes the state of the radiation before the second photon is detected.
Considering again the one photon single state:
\begin{aligned} w^{(2)}(\mathbf r,t) & = s^2\langle \psi | \mathbf{E}^{(-)}(\mathbf{r_1}) \mathbf{E}^{(-)}(\mathbf{r_2}) \mathbf{E}^{(+)}(\mathbf{r_2}) \mathbf{E}^{(+)}(\mathbf{r_1}) | \psi \rangle \\ & = s^2\langle \psi | i^4 \left(\mathbf{e}_\lambda \cdot \mathbf{e}_\lambda\right)^2 \left[\mathscr E^{(1)}_\lambda\right]^4 \left(\mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r_1}} \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r_2}} \mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r_2}} \mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r_1}}\right) | \psi \rangle \\ & = s^2 \left[\mathscr E^{(1)}_\lambda\right]^4 \langle \mathbf 1| e^{i\omega t} \left(\mathbf a_\lambda^\dag \mathbf a_\lambda^\dag \mathbf a_\lambda \mathbf a_\lambda e^{-i\mathbf{k}_\lambda \cdot \mathbf{r_1}} e^{i\mathbf{k}_\lambda \cdot \mathbf{r_1}} e^{-i\mathbf{k}_\lambda \cdot \mathbf{r_2}} e^{i\mathbf{k}_\lambda \cdot \mathbf{r_2}}\right) | \mathbf 1 \rangle e^{-i\omega t} \\ & = s^2\left[\mathscr E^{(1)}_\lambda\right]^4 \langle \mathbf 1| \left(\mathbf a_\lambda^\dag \mathbf a_\lambda^\dag \mathbf a_\lambda \mathbf a_\lambda \right) | \mathbf 1 \rangle e^{i\omega t} e^{-i\omega t} \\ & = s^2\left[\mathscr E^{(1)}_\lambda\right]^4 \langle \mathbf 1| \left(\mathbf a_\lambda^\dag \mathbf a_\lambda^\dag \mathbf a_\lambda \mathbf a_\lambda \right) | \mathbf 1 \rangle = s^2\left[\mathscr E^{(1)}_\lambda\right]^2\mathbf 0| \left(\mathbf a_\lambda^\dag \mathbf a_\lambda \right) | \mathbf 0 \rangle = 0 \end{aligned}
as:
a_\lambda | \mathbf 0 \rangle = 0
So the probability of a double detection is null.
There is an experimental apparatus that can be built for this experiment, with two detectors which are inside the light beam and connected to an electric circuit that monitor and count the pulses, counting also the coincidences of the two detectors going off at the same time during a certain window.
Choosing the window equal to the length of the wavepacket, the detector would register an event if the two detectors fire during the same wavepacket. Considering a number of packet N_{wp} the number of expected average number of detection as:
\begin{aligned} N_1 & = w^{(1)} S_1 T_\lambda N_{wp} \\ N_2 & = w^{(1)} S_2 T_\lambda N_{wp} \end{aligned}
The number of coincidences is given by:
N_C = w^{(2)}S_1 S_2 T_\lambda N_{wp}
For the one photon state these were calculated:
\begin{aligned} N_1 & = \eta \frac{S_1}{S_\lambda} N_{wp} \\ N_1 & = \eta \frac{S_2}{S_\lambda} N_{wp} \\ N_C & = 0 \end{aligned}
If applied the semi-classical model the results for N_1 and N_2 are the same, but for N_C it is very different as the detection rate is constant in this model:
\begin{aligned} N_1 & = w^{(1)} S_1 T_\lambda N_{wp} \\ N_2 & = w^{(1)} S_2 T_\lambda N_{wp} \\ N_c & = w^{(2)} S_1 S_2 T_\lambda^2 N_{wp} \\ & = \left[w^{(1)}\right]^2 S_1 S_2 T_\lambda^2 N_{wp} \ne 0 \end{aligned}
Amplitude evolution
Considering a single mode plain wave and defining the quantities:
\begin{aligned} & \alpha_\lambda(t) | \psi(t) \rangle = \mathbf a_\lambda | \psi(t) \rangle \\ & \langle \psi(t) \bar \alpha(t) = \langle \psi(t) | \mathbf a_\lambda^\dag \end{aligned}
It is possible to express the electric field \mathbf E(\mathbf r,t) = \langle \psi(t) | \mathbf E(\mathbf r) | \psi(t) \rangle based on these quantities:
\begin{aligned} \mathbf E(\mathbf r,t) & = \langle \psi(t) | \mathbf E(\mathbf r) | \psi(t) \rangle = \langle \psi(t) | i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) | \psi(t) \rangle \\ & = i\mathscr E^{(1)}_\lambda \left(\mathbf \alpha_\lambda(t) e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \bar \alpha_\lambda(t) e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \langle \psi(t) |\mathbf{e}_\lambda | \psi(t) \rangle\\ & = i\mathscr E^{(1)}_\lambda \left(\mathbf \alpha_\lambda(t) e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \bar \alpha_\lambda(t) e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \end{aligned}
The general state at time zero can be expanded in the basis as:
| \psi(0) \rangle = \sum_{n=0}^\infty c_n | \mathbf n \rangle
To express |\psi(t)\rangle at time t, we need to consider the time evolution operator U(t). For a Hamiltonian H, the time evolution operator in the Schrödinger picture is U(t) = e^{-iHt/\hbar}. Therefore, the state |\psi(t)\rangle can be expressed as:
|\psi(t)\rangle = U(t) |\psi(0)\rangle = e^{-iHt/\hbar} \sum_{n=0}^\infty c_n |\mathbf{n}\rangle
If |\mathbf{n}\rangle are eigenstates of the Hamiltonian H with eigenvalues E_n, such that H|\mathbf{n}\rangle = E_n|\mathbf{n}\rangle, the expression can be simplified using the fact that e^{-iHt/\hbar}|\mathbf{n}\rangle = e^{-iE_nt/\hbar}|\mathbf{n}\rangle:
|\psi(t)\rangle = \sum_{n=0}^\infty c_n e^{-iE_nt/\hbar} |\mathbf{n}\rangle
For a quantum harmonic oscillator, the eigenvalues E_n are given by:
E_n = \hbar \omega \left(n + \frac{1}{2}\right), \quad N \in \mathbb N
substituting:
|\psi(t)\rangle = \sum_{n=0}^\infty c_n e^{-i \omega \left(n + \frac{1}{2}\right)t} |\mathbf{n}\rangle
Using the same unitary time evolution operator \alpha(t) and \bar \alpha(t) can be expressed as:
\begin{aligned} & \alpha_\lambda (t) | \psi(t) \rangle = \alpha_\lambda e^{-i\omega_\lambda t} | \psi(t) \rangle \\ & \langle \psi(t) | \bar \alpha_\lambda (t) = \langle \psi(t) | \bar \alpha_\lambda e^{i\omega_\lambda t} \end{aligned}
And the expectation of electric field \mathbf E(\mathbf r,t):
\begin{aligned} \mathbf E(\mathbf r,t) & = i\mathscr E^{(1)}_\lambda \left(\mathbf \alpha_\lambda(t) e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \bar \alpha_\lambda(t) e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \\ & = i\mathscr E^{(1)}_\lambda \left(\mathbf \alpha_\lambda e^{-i\omega_\lambda t} e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \bar \alpha_\lambda e^{i\omega_\lambda t} e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \\ & = i \mathscr E^{(1)}_\lambda \left(\mathbf \alpha_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r} -i\omega_\lambda t} - \bar \alpha_\lambda e^{-i\mathbf{k}_\lambda \cdot \mathbf{r} + i\omega_\lambda t} \right) \end{aligned}