One Photon Multimode Interference
Interference for a single mode photon was already described here; similarly it is possible to do the same analysis for a multimode wave packet:
\begin{aligned} & | \psi(t_0) \rangle = | \mathbf 1 \rangle = \sum_\lambda c_\lambda | \mathbf 1_\lambda \rangle \\ & c_\lambda = \frac{Ke^{i\omega_\lambda t_0}}{(\omega_\lambda - \omega_0) - i\frac{\Gamma}{2}}, \quad k=\sqrt{\frac{c\Gamma}{L}} \end{aligned}
The experimental setup is for this case a Mach-Zendher interferometer, with a single mode entering in the input channel (1).
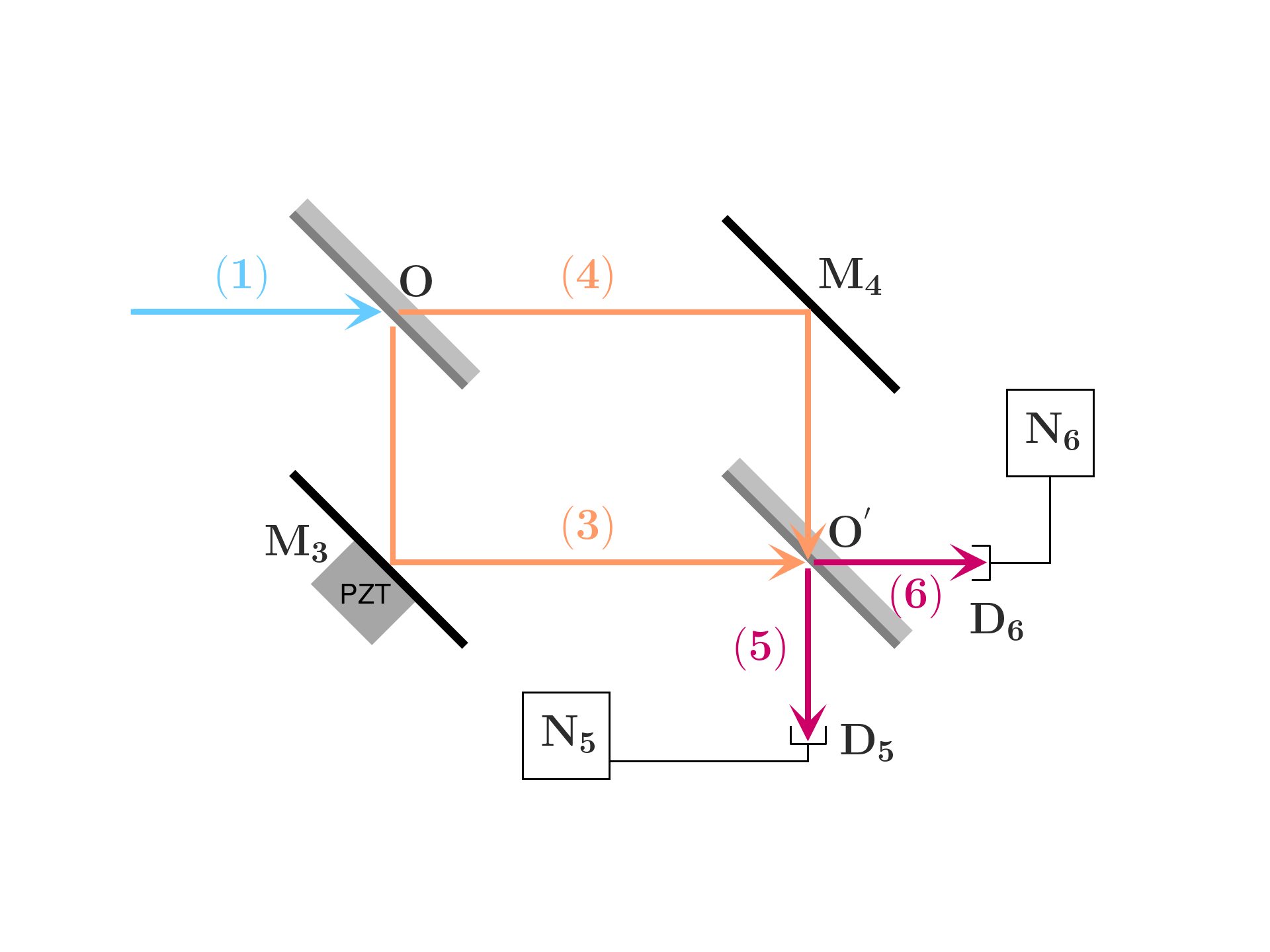
We will be using the Heisenberg formalism for the electric field:
\mathbf{E}(\mathbf{r})^{(+)} = \sum_\lambda i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \mathbf a_\lambda(0) e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)}
The input state is:
| \Psi_{12} \rangle = | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2
We can perform a similar calculation as the one photon case.
All the waves have the same polarization and the time component can be factored out. We start from the semi-classical model and consider the relationship at the first beam splitter at point O:
\begin{aligned} E_3^{(+)} & = r\,E_1^{(+)}(O) \\ E_4^{(+)} & = t\,E_1^{(+)}(O) \end{aligned}
Considering the one at the second beam splitter at point O^{'}:
\begin{aligned} E_5^{(+)} & = -r\,E_3^{(+)}(O^{'}) + t\,E_4^{(+)}(O^{'}) \\ E_6^{(+)} & = t\,E_3^{(+)}(O^{'}) + r\,E_4^{(+)}(O^{'}) \end{aligned}
The last step is to take into account the propagation from O to O^{'}:
\begin{aligned} E_3^{(+)}(O^{'}) & = E_3^{(+)}\left(O, t-\frac{L_3}{c}\right) \\ E_4^{(+)}(O^{'}) & = E_4^{(+)}\left(O, t-\frac{L_4}{c}\right) \end{aligned}
which takes into account that in the vacuum or in a non dispersive medium the light propagate at speed c; that will allow to express the amplitude as function of the amplitudes in channel (1):
\begin{aligned} E_5^{(+)} & = -R\,E_1^{(+)}\left(O, t-\frac{L_3}{c}\right) + T\,E_1^{(+)}\left(O, t-\frac{L_4}{c}\right) \\ E_6^{(+)} & = \sqrt{RT}\left[\,E_1^{(+)}\left(O, t-\frac{L_3}{c}\right) + E_1^{(+)}\left(O, t-\frac{L_4}{c}\right)\right] \end{aligned}
Then it is possible to quantize these relationship; in general the vacuum channel (2) should be considered, but in this case is not contributed to the result as the state will have an annihilator operator on the vacuum and therefore not give any contribution:
\begin{aligned} \mathbf E_5^{(+)} & = -R\,\mathbf E_1^{(+)}\left(O, t-\frac{L_3}{c}\right) + T\,\mathbf E_1^{(+)}\left(O, t-\frac{L_4}{c}\right) \\ \mathbf E_6^{(+)} & = \sqrt{RT}\left[\mathbf E_1^{(+)}\left(O, t-\frac{L_3}{c}\right) + \mathbf E_1^{(+)}\left(O, t-\frac{L_4}{c}\right)\right] \end{aligned}
The photodection probability can be then computed:
\begin{aligned} w^{(1)}(D_5 ,t) & = s \left\|\mathbf{E}_5^{(+)}(D_5, t) | \Psi_{12} \rangle \right\|^2 \\ & = s \left\|-R\,E_1^{(+)}\left(O, t-\frac{L_3}{c}\right) +T\, E_1^{(+)}\left(O, t-\frac{L_4}{c}\right) | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 \right\|^2 \\ & = s \left\|-R\,f(\tau_3) + T f(\tau_4) | \mathbf 0 \rangle \right\|^2 \\ & = s \left|-R\,f(\tau_3) + T f(\tau_4) \right|^2 \end{aligned}
where we used the calculation that:
\mathbf E_1^{(+)}(\tau_i) = f(\tau_i) \propto H(\tau)e^{-\frac{\Gamma}{2}\tau_i}e^{-i\omega_0 \tau_i}
with \tau_3 = t - \frac{L_3}{c} and \tau_4 = t - \frac{L_4}{c}.
In the case of balanced beam splitter (R = T = \frac{1}{2}) the expression is:
\begin{aligned} w^{(1)}(D_5 ,t) & = \frac{s}{4} \left(\left|f(\tau_3)\right|^2 + \left|f(\tau_4)\right|^2 + f(\tau_3)f(\bar \tau_4) + f(\bar \tau_3)f(\tau_4)\right) \\ & = \frac{s}{2}\left|f(\langle \tau \rangle)\right|^2 \left(2 - 2\cos\left(\omega_0 \frac{\delta L}{c}\right)\right) \\ &= \frac{s}{2}\left|f(\langle \tau \rangle)\right|^2 \left(1 - \cos\left(\omega_0 \frac{\delta L}{c}\right)\right) \end{aligned}
where we introduced the average \langle L \rangle = \frac{L_3 + L_4}{2}, \delta L = L_3 - L_4 and the assumption \frac{\delta L}{c} \ll \Gamma^{-1} (which is reasonable when considering visible light and atomic transition) so that (with \langle \tau \rangle = t - \frac{\langle L \rangle}{c}):
\begin{aligned} & f(\tau_3) \propto f(\langle \tau \rangle)e^{-i\omega_0 \frac{\delta L}{2c}} \\ & f(\tau_4) \propto f(\langle \tau \rangle)e^{+i\omega_0 \frac{\delta L}{2c}} \end{aligned}
The simplification done one \tau is not valid for the phase factor.
Integrating over the detector and inserting the correct prefactor and the global quantum efficiency \varepsilon, the rate of photodetection at D_5 is:
\frac{\mathrm dP}{\mathrm dt}(D_5,t) = \frac{\varepsilon}{\Gamma}H\left(t - t_0 - \frac{\langle L \rangle}{c} \right) e^{-\Gamma \left(t - t_0 - \frac{\langle L \rangle}{c} \right)} \sin^2\left(\omega_0 \frac{\delta L}{2c}\right)
Using the formula for half-angles. Integrating over the gate we obtain the probability of phototection per pulse:
P(D_5) = \varepsilon \sin^2\left(\omega_0 \frac{\delta L}{2c}\right)
A similar calculation for D_6 gives:
\begin{aligned} & \frac{\mathrm dP}{\mathrm dt}(D_5,t) = \frac{\varepsilon}{\Gamma}H\left(t - t_0 - \frac{\langle L \rangle}{c} \right) e^{-\Gamma \left(t - t_0 - \frac{\langle L \rangle}{c} \right)} \cos^2\left(\omega_0 \frac{\delta L}{2c}\right) \\ & P(D_6) = \varepsilon \cos^2\left(\omega_0 \frac{\delta L}{2c}\right) \end{aligned}
The probabilities of both detectors summed gives a constant detection equal to the global quantum efficiency.