One Photon Interference
Beam-splitter (semi-reflecting mirror)
Mach-Zehnden Interferometer
Beam-splitter (semi-reflecting mirror)
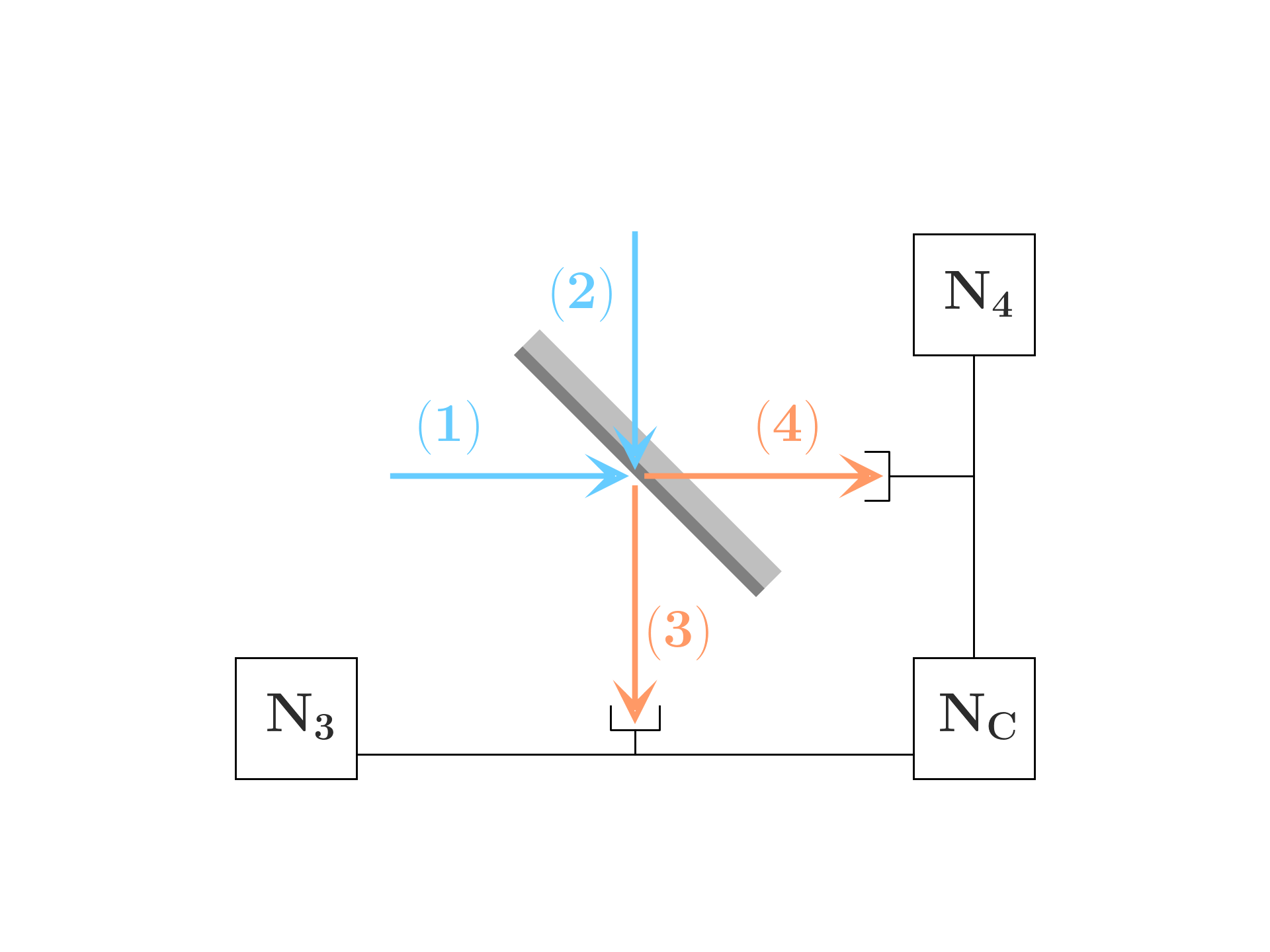
Consider a light beam traveling horizontally from left to right and incident on a semi-reflecting mirror placed at the origin. Upon encountering the mirror, the beam splits into two: one transmitted beam continuing downward from the origin, and one reflected beam continuing horizontally to the right from the origin.
Similarly, there is a second input port located above the origin, through which a second incident beam would travel vertically downward toward the origin. This second beam would also split upon encountering the mirror, resulting in a transmitted beam continuing horizontally to the right and a reflected beam continuing downward from the origin.
For simplicity, we assume that all beams are polarized perpendicularly to the plane of the figure, allowing us to treat the electric fields as scalar quantities. Additionally, we assume that each beam corresponds to a traveling plane-wave mode, with all modes having the same frequency.
Classical optics
In classical optics, an input mode (1) is partially reflected in mode (3) and partially transmitted in mode (4); there is also mode (2) (symmetric to mode (1)) which lead to a similar setup with transmission and reflection inverted.
In classical optics it is possible to express the output beams as function of the input beams by imposing continuity relations at the interface of the various layers, and it is sufficient to give the relations between the complex amplitudes, and for convenience of the formulas the interface is considered at \mathbf r = 0 so that all the complex spatial exponential are equal to one, and since the frequencies are the same, the time factor e^{i\omega t} can factorized left and right and ignored:
\begin{aligned} E_3^{(+)} & = r\,E_1^{(+)} + t\, E_2^{(+)} \\ E_4^{(+)} & = t\,E_1^{(+)} - r\, E_2^{(+)} \end{aligned}
where the coefficient r stands for reflection and t for transmission.
Considering the beam splitter lossless, there is energy conservation, and, if there is a single wave (1) or single wave (2) leads to the relations:
\begin{aligned} & \left|E_3^{(+)}\right|^2 + \left|E_4^{(+)}\right|^2 = \left|E_1^{(+)}\right|^2 \\ & \left|E_3^{(+)}\right|^2 + \left|E_4^{(+)}\right|^2 = \left|E_2^{(+)}\right|^2 \end{aligned}
which translate to:
\begin{aligned} & r^2 + t^2 = 1 \\ & R + T = 1 \end{aligned}
where the lower cases are the amplitude coefficients, the upper case the intensity coefficients.
The minus sign in the reflection for wave (2) ensure the energy conservation in the presence of two waves:
\begin{aligned} & \left|E_3^{(+)}\right|^2 = r^2\left|E_1^{(+)}\right|^2 + t^2\left|E_2^{(+)}\right|^2 + rt \left|E_1^{(+)}\right| \left|E_2^{(+)}\right|\\ & \left|E_4^{(+)}\right|^2 = t^2\left|E_1^{(+)}\right|^2 -r^2\left|E_2^{(+)}\right|^2 - + rt \left|E_1^{(+)}\right| \left|E_2^{(+)}\right| \\ & \left|E_4^{(+)}\right|^2 + \left|E_3^{(+)}\right|^2 = (r^2 + t^2)\left|E_1^{(+)}\right|^2 + (r^2 + t^2)\left|E_2^{(+)}\right|^2 \\ & \left|E_4^{(+)}\right|^2 + \left|E_3^{(+)}\right|^2 = \left|E_1^{(+)}\right|^2 + \left|E_2^{(+)}\right|^2 \end{aligned}
The relation can be written in matrix form:
\begin{bmatrix} E_3^{(+)} \\ E_4^{(+)} \end{bmatrix} = \begin{bmatrix} r & t \\ t & -r \end{bmatrix} \begin{bmatrix} E_1^{(+)} \\ E_2^{(+)} \end{bmatrix}
or in short:
\mathbf E_{\text{out}} = \mathbf S \; \mathbf E_{\text{in}}
The conservation of energy is requiring that the matrix \mathbf S is unitary, as the norm is conserved, and if the matrix is unitary its inverse conjugate is the transposed:
\mathbf{\bar S}^{-1} = \mathbf S^{T} \; \Longleftrightarrow \; \sum_i \bar s_{ij}s_{ik} = \delta_{jk}
As example, lets consider the state with one photon state in mode (1) and no photon in mode (2); this can be modeled classically as:
\mathbf E_1^{(+)}(\mathbf r_1,t) = \mathbf e_\lambda \mathcal E_\lambda(0) e^{-i(\mathbf k_\lambda \cdot \mathbf r_1 - \omega_\lambda t)}
using the rate of photodetection in the semiclassical model:
w^{(1)}(\mathbf r_3,t) = s\left|\mathbf E^{(+)}_3(\mathbf r,t)\right|^2 = sR\left|\mathbf E^{(+)}_1(\mathbf r,t)\right|^2
Integrating over the volume of the wavepacket and multiplying by the number of wavepackets, we obtain the number of detection in the reflected output (3):
N_3 = Rs\left|\mathcal E(0)\right|^2 S_1 T_1 N_{wp}
A similar calculation yields to:
N_4 = Ts\left|\mathcal E(0)\right|^2 S_1 T_1 N_{wp}
It is possible to compute the number of double detections in the channel (3) and (4):
w^{(2)}(\mathbf r_3,t,\mathbf r_4,t) = w^{(1)}(\mathbf r_3,t) w^{(1)}(\mathbf r_4,t) = RTs^2\left|\mathcal E(0)\right|^4
The total number of detections is obtained integrating twice on the wavepacket volume:
N_C = RTs^2\left|\mathcal E(0)\right|^4 S_1^2 T_1^2 N_{wp} = \frac{N_3N_4}{N_{wp}}
Quantum optics
In quantum optics, the state space can be described by a state | \Psi_{12} \rangle which is a state associated with the two modes (1) and (2) or in another described by the state | \Psi_{34}\rangle with the two modes associated to (3) and (4).
Trying to find a linear transformation \mathbf U (a change of basis) to go from the input states to the output is quickly giving a very large matrix, as all the superposition of all states need to be considered; there is however a simpler method which involve transforming the observables.
Let’s assume the objective is to calculate the output observable \langle \mathbf O_o \rangle; it can be written as:
\begin{aligned} \langle \mathbf O_o \rangle & = \langle \psi_o | \mathbf O_o | \psi_o \rangle = \left(\langle \psi_i | \mathbf U^\dag\right) | \mathbf O_o | \left(\mathbf U | \psi_i \rangle\right) \\ & = \langle \psi_i | \left(\mathbf U^\dag| \mathbf O_o | \mathbf U \right)| \psi_i \rangle = \langle \psi_i | \mathbf O_i | \psi_i \rangle \end{aligned}
where:
\mathbf O_i \equiv \mathbf U^\dag| \mathbf O_o | \mathbf U
This transformation is how operators transform when there is a change of basis; then the only necessary quantity to know is how to express the observable in the input space.
This framework can be applied in the case of the beam splitter, for example to calculate the photo detection signal w^{(1)} in the output channel (4):
\mathbf O_o = E_4^{(-)}E_4^{(+)}
This is in the output space, and the transformation to go from the input space to the output space was previously calculated for the classical field and it is \mathbf S and therefore the output operators can be written now as function of the input operators:
\begin{aligned} \mathbf E_3^{(+)} & = r\,\mathbf E_1^{(+)} + t\,\mathbf E_2^{(+)} \\ \mathbf E_4^{(+)} & = t\,\mathbf E_1^{(+)} - r\,\mathbf E_2^{(+)} \end{aligned}
Now these are all operators; this result can be generalized to optic systems in which light is propagating, where the field transformation between input and output operators is the same as the transformation between input and output classical fields.
The relation holds also for the averages:
\begin{bmatrix} \langle \mathbf E_3^{(+)} \rangle \\ \langle \mathbf E_4^{(+)} \rangle \end{bmatrix} = \begin{bmatrix} \mathbf S \end{bmatrix} \begin{bmatrix} \langle \mathbf E_1^{(+)} \rangle \\ \langle \mathbf E_2^{(+)} \rangle \end{bmatrix}
This relation, which applies also to quasi-classical quantum states that behave consistently with the classical counterpart and make link between classical and quantum optics
These relations also guarantee that the commutators of the creation and annihilation operators respect the necessary commutators relations (in this case too many exponential are one or can be factored due to the frequency and axes choices):
\begin{aligned} \mathbf a_3 & = r\,\mathbf a_1 + t\,\mathbf a_2 \\ \mathbf a_4 & = t\,\mathbf a_1 - r\,\mathbf a_2 \end{aligned}
Using the commutator relation in the input space:
[\mathbf{a}_1, \mathbf{a}_1] = 1, \quad [\mathbf{a}_2, \mathbf{a}_2] = 1, \quad [\mathbf{a}_1, \mathbf{a}_2] = 0
The commutator [\mathbf{a}_3, \mathbf{a}_3] is:
\begin{aligned} [\mathbf{a}_3, \mathbf{a}_3] &= [r \mathbf{a}_1 + t \mathbf{a}_2, r \mathbf{a}_1 + t \mathbf{a}_2] \\ &= r^2 [\mathbf{a}_1, \mathbf{a}_1] + rt ([\mathbf{a}_1, \mathbf{a}_2] + [\mathbf{a}_2, \mathbf{a}_1]) + t^2 [\mathbf{a}_2, \mathbf{a}_2] \\ &= r^2 (1) + t^2 (1) \\ &= r^2 + t^2 \\ &= 1 \end{aligned}
The commutator [\mathbf{a}_4, \mathbf{a}_4] is:
\begin{aligned} [\mathbf{a}_4, \mathbf{a}_4] &= [t \mathbf{a}_1 - r \mathbf{a}_2, t \mathbf{a}_1 - r \mathbf{a}_2] \\ &= t^2 [\mathbf{a}_1, \mathbf{a}_1] - rt ([\mathbf{a}_1, \mathbf{a}_2] + [\mathbf{a}_2, \mathbf{a}_1]) + r^2 [\mathbf{a}_2, \mathbf{a}_2] \\ &= t^2 (1) + r^2 (1) \\ &= t^2 + r^2 \\ &= 1 \end{aligned}
The commutator [\mathbf{a}_3, \mathbf{a}_4] is
\begin{aligned} [\mathbf{a}_3, \mathbf{a}_4] &= [r \mathbf{a}_1 + t \mathbf{a}_2, t \mathbf{a}_1 - r \mathbf{a}_2] \\ &= rt ([\mathbf{a}_1, \mathbf{a}_1] - [\mathbf{a}_1, \mathbf{a}_2] + [\mathbf{a}_2, \mathbf{a}_1] - [\mathbf{a}_2, \mathbf{a}_2]) \\ &= rt (1 - 0 + 0 - 1) \\ &= rt (0) \\ &= 0 \end{aligned}
As example, lets consider the state with one photon state in mode (1) (| \mathbf 1 \rangle_1) and no photon in mode (2) (| \mathbf 0 \rangle_2):
| \Psi_{12} \rangle = | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2
Single detection
The objective it to calculate the rate of single detection at output (4):
w^{(1)}(\mathbf r_4,t) = s \left\| \mathbf E_4^{(+)} | \Psi_o \rangle \right\|^2
It is possible to express it as function of the input states:
\begin{aligned} w^{(1)}(\mathbf r_4,t) & = s \left\| t\,\mathbf E_1^{(+)} - r\,\mathbf E_2^{(+)} | \Psi_{12} \rangle \right\|^2 \\ & = s \left[ \mathscr E^{(1)}\right]^2 \left\|\left( t\,\mathbf a_1 - r\,\mathbf a_2 \right) \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 \right\|^2 \\ & = s \left[ \mathscr E^{(1)}\right]^2 \left\| t\,\mathbf 0 \rangle_1 | \mathbf 0 \rangle_2 \right\|^2 = s \left[ \mathscr E^{(1)}\right]^2 t^2 = s \left[ \mathscr E^{(1)}\right]^2 T \end{aligned}
which was obtained using the shorthand:
\begin{aligned} \mathbf a_1 | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 & = \mathbf a_1 \otimes \mathbf I | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 = \mathbf a_1 \otimes | \mathbf 1 \rangle_1 \mathbf I \otimes | \mathbf 0 \rangle_2 = | \mathbf 0 \rangle_1 | \mathbf 0 \rangle_2 \\ \mathbf a_2 | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 & = \mathbf I \otimes \mathbf a_2 | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 = \mathbf I \otimes \mathbf 1 \rangle_1 \mathbf a_2 \otimes | \mathbf 0 \rangle_2 = | \mathbf 1 \rangle_1 | 0 = 0 \end{aligned}
Integrating over the duration of the wavepacket yields to the probability for each wavepacket:
P_4 = \eta T
And multiplying for the number of N_{wp} wavepackets sent during an experiments, the total count is:
N_4 = \eta T N_{wp}
Similarly, for the detector (3):
\begin{aligned} w^{(1)}(\mathbf r_3,t) & = s \left\| r\,\mathbf E_1^{(+)} + t\,\mathbf E_2^{(+)} | \Psi_{12} \rangle \right\|^2 \\ & = s \left[ \mathscr E^{(1)}\right]^2 \left\|\left( r\,\mathbf a_1 + t\,\mathbf a_2 \right) \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 \right\|^2 \\ & = s \left[ \mathscr E^{(1)}\right]^2 \left\| r\,\mathbf 0 \rangle_1 | \mathbf 0 \rangle_2 \right\|^2 = s \left[ \mathscr E^{(1)}\right]^2 r^2 = s \left[ \mathscr E^{(1)}\right]^2 R \end{aligned}
The total count is:
N_3 = \eta R N_{wp}
Double detection
The objective it to calculate now the rate of double detection at output (4):
\begin{aligned} w^{(2)}(\mathbf r_3, \mathbf r_4,t) & = s^2 \left\| \mathbf E_3^{(+)} \mathbf E_4^{(+)} | \Psi_o \rangle \right\|^2 \\ & = s^2 \left\| \left(r\,\mathbf E_1^{(+)} + t\,\mathbf E_2^{(+)}\right)\left( t\,\mathbf E_1^{(+)} - r\,\mathbf E_2^{(+)} \right) | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 \right\|^2 \\ & = s^2 \left\| rt\,\mathbf E_1^{(+)} \mathbf E_1^{(+)} | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 \right\|^2 = 0 \end{aligned}
as applying twice the annihilator operators to a single photon gives a null result; a photon cannot be detected twice:
N_C = 0
Comparison
It is possible to compare the results between the semiclassical case and the full quantum case: while for a single detection the results are similar, for double detection the results are extremely different, as in the case of semi-classical model the probability is not null, while for the quantum optics case the results is always zero.
Mach-Zehnden interferometer
A Mach-Zehnder interferometer is an optical device used to measure minute differences in phase or path length. At its core, the apparatus consists of two beam splitters and two mirrors arranged to split and then recombine a light beam, usually from a coherent source like a laser.
The journey begins when an incoming beam, entering in mode (1), encounters the first beam splitter. This component divides the light into two separate paths, directing beams along paths (3) and (4). Each path is equipped with two mirrors \text{M}_3 and \text{M}_4 that reflect the beams to the second beam splitter. This recombination is sensitive to the phase differences introduced along the paths, typically manipulated by adjusting the position of one of the mirrors with a piezo-electric transducer (\text{PZT}). This allows for extremely precise control over the path length differences, down to sub-nanometer adjustments.
The recombined beams exit the second beam splitter in modes (5) and (6), leading to detectors \text{D}_5 and \text{D}_6. These detectors measure the interference pattern, which depends on the phase difference between the two paths, providing insights into physical changes that affect the path length or phase along one of the beams. This precise measurement capability makes the Mach-Zehnder interferometer a powerful tool in experimental physics and engineering.
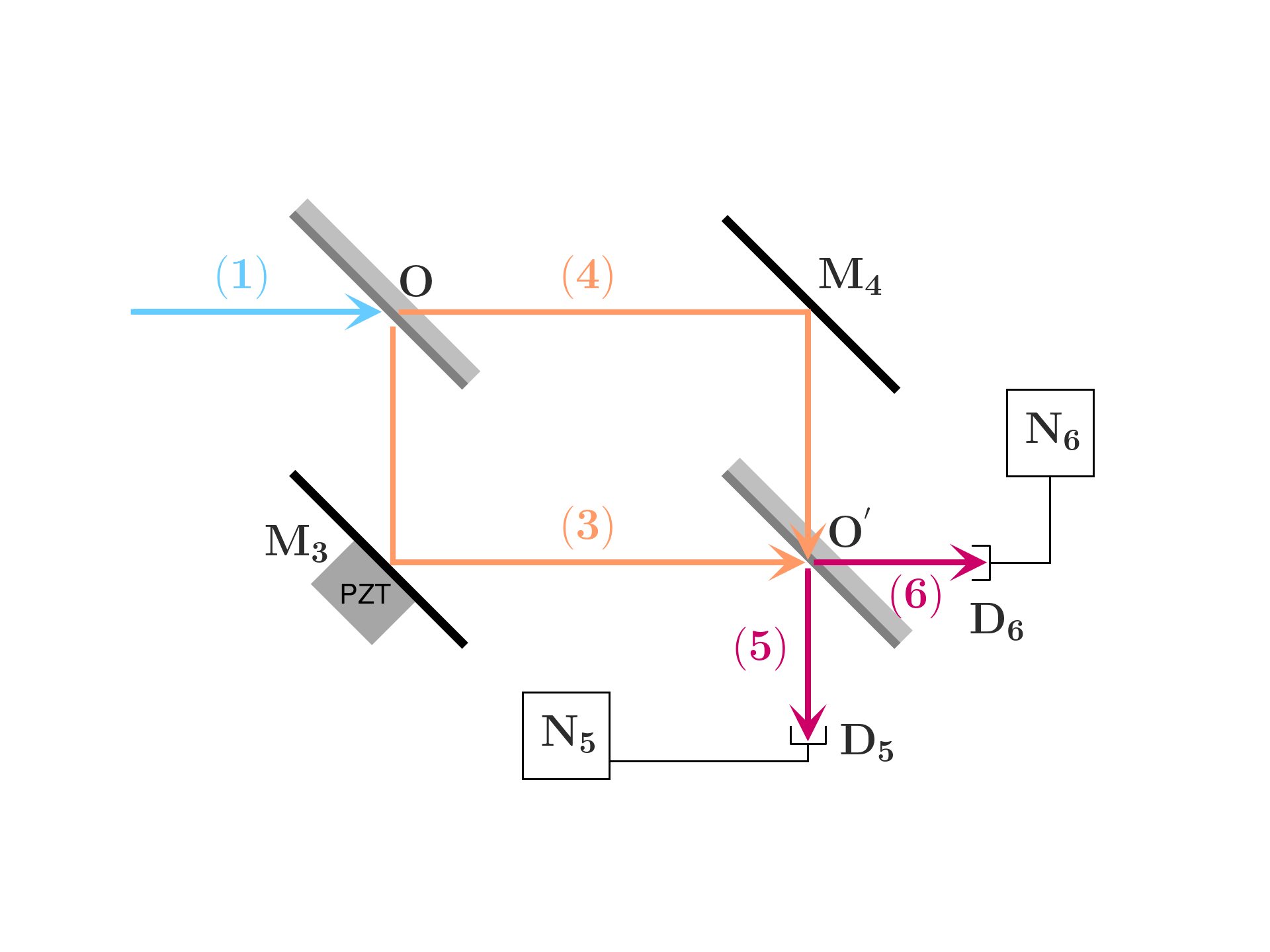
The critical length is the difference of the length of paths (3) and (4):
\delta L = \overline {OM_4O^{'}} - \overline{OM_3O^{'}}
This path difference can be varied with greater accuracy using a transducer.
The total number of count in each detector varies as function of \delta L but the total number is constant:
\begin{aligned} N_5 & = N_{\text{tot}} f(\delta L) \\ N_6 & = N_{\text{tot}}\left[ 1 - f(\delta L)\right] \end{aligned}
Classical optics
The calculation in classical optics is quite standard, but some of it will be used in the quantum calculation so it worth to be done in details.
All the waves have the same polarization and the time component can be factored out.
Consider the relationship at the first beam splitter at point O:
\begin{aligned} E_3^{(+)} & = r\,E_1^{(+)} \\ E_4^{(+)} & = t\,E_1^{(+)} \end{aligned}
After propagating of a distance L, the field at point O^{'} have an amplitude which depends from the path length:
\begin{aligned} E_3^{(+)}(O^{'}) & = e^{ikL_3}E_3^{(+)} \\ E_4^{(+)}(O^{'}) & = e^{ikL_4}E_4^{(+)} \end{aligned}
Considering the one at the second beam splitter at point O^{'}:
\begin{aligned} E_5^{(+)} & = -r\,E_3^{(+)}(O^{'}) + t\,E_4^{(+)}(O^{'}) \\ E_6^{(+)} & = t\,E_3^{(+)}(O^{'}) + r\,E_4^{(+)}(O^{'}) \end{aligned}
The reason of the sign difference is because the second beam splitter is reversed compared to the first one; the transformation is still unitary and this setup guarantees a symmetry since each beam is passing once through the dielectric material while if the second splitter would not be reversed one beam would pass twice and the other would not pass at all; this schema is necessary for non-monochromatic light due to the dielectric dispersion.
Then, with the relation above it is possible to express the output beam as function of E_1^{(+)}:
\begin{aligned} E_5^{(+)} & = -r\,E_3^{(+)}(O^{'}) + t\,E_4^{(+)}(O^{'}) = -r\,e^{ikL_3}E_3^{(+)} + t\,e^{ikL_4}E_4^{(+)} \\ & = -r^2\,e^{ikL_3}E_1^{(+)} + t^2\,e^{ikL_4}E_1^{(+)} \\ E_6^{(+)} & = t\,E_3^{(+)}(O^{'}) + r\,E_4^{(+)}(O^{'}) = t\,e^{ikL_3}E_3^{(+)} + r\,e^{ikL_4}E_4^{(+)} \\ & = rt\,e^{ikL_3}E_1^{(+)} + rt\,e^{ikL_4}E_1^{(+)} \end{aligned}
Taking the square of the field gives the detection rate for D_5:
\begin{aligned} \left| E_5^{(+)} \right|^2 & = \left|E_1^{(+)}\right|^2 \left|-r^2\,e^{ikL_3} + t^2\,e^{ikL_4}\right|^2 = \left|E_1^{(+)}\right|^2 \left|-R\,e^{ikL_3} + T\,e^{ikL_4}\right|^2 \\ & = \left|E_1^{(+)}\right|^2 \left[R^2 + T^2 -RT\left(\,e^{ik(L_3-L_4)} + e^{-ik(L_3-L_4)}\right)\right] \\ & = \left|E_1^{(+)}\right|^2 \left(R^2 + T^2 \right)\left(1 - 2\frac{RT}{R^2+T^2}\cos(k\delta L)\right) \\ & = \left|E_1^{(+)}\right|^2 \left(R^2 + T^2 \right)\left(1 - V\cos(k\delta L)\right) \end{aligned}
where we define:
V \equiv 2\frac{RT}{R^2+T^2}
the visibility of the fringes.
Repeating the same calculation for D_6:
\begin{aligned} \left| E_6^{(+)} \right|^2 & = \left|E_1^{(+)}\right|^2 \left|rt\,e^{ikL_3} + rt\,e^{ikL_4}\right|^2 \\ & = \left|E_1^{(+)}\right|^2 RT \left[\left(\,e^{ik(L_3-L_4)} + e^{-ik(L_3-L_4)}\right)\right] \\ & = \left|E_1^{(+)}\right|^2 2RT \left(\cos(k\delta L)\right) \\ & = \left|E_1^{(+)}\right|^2 \left(R^2 + T^2 \right)\left(2\frac{RT}{R^2+T^2}\cos(k\delta L)\right) \\ & = \left|E_1^{(+)}\right|^2 \left(R^2 + T^2 \right)\left(V\cos(k\delta L)\right) \end{aligned}
The total sum N_5 + N_6 is independent from the distance L:
N_{\text{tot}} = N_5 + N_6 = \left|E_1^{(+)}\right|^2 \left(R^2 + T^2 \right)\left(1 - V\cos(k\delta L)\right) + \left|E_1^{(+)}\right|^2 \left(R^2 + T^2 \right)\left(V\cos(k\delta L)\right) = \left|E_1^{(+)}\right|^2 \left(R^2 + T^2 \right)
For balanced beam-splitters, which have equal reflection and transmission R = T = 0.5, the visibility is unitary V = 1.
Quantum optics
It is possible to perform the same calculation, considering an input source constituted by one photon in mode (1) and no photon in mode (2):
| \Psi_{12} \rangle = | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2
It is possible to write the same equation as in the semi-classical case, with the difference that now the classical field is replaced by field operators, and it is not possible to ignore the status with no photons because the vacuum state plays a role in quantum optics:
\begin{aligned} \mathbf E_3^{(+)} & = r\,\mathbf E_1^{(+)} + t\,\mathbf E_2^{(+)} \\ \mathbf E_4^{(+)} & = t\,\mathbf E_1^{(+)} - r\,\mathbf E_2^{(+)} \end{aligned}
The propagation factor between O and O^{'} is the same as the semi-classical case:
\begin{aligned} \mathbf E_3^{(+)}(O^{'}) & = e^{ikL_3}\mathbf E_3^{(+)} \\ \mathbf E_4^{(+)}(O^{'}) & = e^{ikL_4}\mathbf E_4^{(+)} \end{aligned}
Considering the one at the second beam splitter at point O^{'}:
\begin{aligned} \mathbf E_5^{(+)} & = -r\,\mathbf E_3^{(+)}(O^{'}) + t\,\mathbf E_4^{(+)}(O^{'}) \\ \mathbf E_6^{(+)} & = t\,\mathbf E_3^{(+)}(O^{'}) + r\,\mathbf E_4^{(+)}(O^{'}) \end{aligned}
Then, with the relation above it is possible to express the output beam as function of \mathbf E_1^{(+)} and \mathbf E_2^{(+)}:
\begin{aligned} \mathbf E_5^{(+)} & = -r\,\mathbf E_3^{(+)}(O^{'}) + t\,\mathbf E_4^{(+)}(O^{'}) = -r\,e^{ikL_3}\mathbf E_3^{(+)} + t\,e^{ikL_4}\mathbf E_4^{(+)} \\ & = -r^2\,e^{ikL_3}\mathbf E_1^{(+)} + t^2\,e^{ikL_4}\mathbf E_1^{(+)} - rt,e^{ikL_3}\mathbf E_2^{(+)} + rt,e^{ikL_4}\mathbf E_2^{(+)}\\ \mathbf E_6^{(+)} & = t\,\mathbf E_3^{(+)}(O^{'}) + r\,\mathbf E_4^{(+)}(O^{'}) = t\,e^{ikL_3}\mathbf E_3^{(+)} + r\,e^{ikL_4}\mathbf E_4^{(+)} \\ & = rt\,e^{ikL_3}\mathbf E_1^{(+)} + rt\,e^{ikL_4}\mathbf E_1^{(+)} + r^2\,e^{ikL_3}\mathbf E_2^{(+)} + t^2\,e^{ikL_4}\mathbf E_2^{(+)} \end{aligned}
To compute the rate of detection it is necessary to apply these operators to the input state; since the field is proportional to the annihilator operators, when apply to the state (2) is gives zero:
\mathbf E_2^{(+)} | \Psi_{12} \rangle = \mathbf E_2^{(+)} | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 = 0
and therefore in this example there is no contribution to the vacuum state in (2), but this is not a general solution, the vacuum state need to be always considered. Therefore, the remaining expression for the detection rate are:
\begin{aligned} \mathbf E_5^{(+)} | \Psi_{12} \rangle & = \left(-r^2\,e^{ikL_3} + t^2\,e^{ikL_4}\right)\mathbf E_1^{(+)} | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 \\ & = -i \mathscr E^{(1)}\left(-r^2\,e^{ikL_3} + t^2\,e^{ikL_4}\right) | \mathbf 0 \rangle \\ \mathbf E_6^{(+)} | \Psi_{12} \rangle & = \left(rt\,e^{ikL_3} + rt\,e^{ikL_4}\right)\mathbf E_1^{(+)} | \mathbf 1 \rangle_1 | \mathbf 0 \rangle_2 \\ & = -i \mathscr E^{(1)}\left(rt\,e^{ikL_3} + rt\,e^{ikL_4}\right) | \mathbf 0 \rangle \end{aligned}
Finally the rate of detection can be calculated:
\begin{aligned} \left\|\mathbf E_5^{(+)} | \mathbf 1 \rangle \right\|^2 & = \left[\mathscr E^{(1)}\right]^2 \left(-r^2\,e^{ikL_3} + t^2\,e^{ikL_4}\right)^2 = \left[\mathscr E^{(1)}\right]^2 \left(-R\,e^{ikL_3} + T\,e^{ikL_4}\right)^2 \\ & = \left[\mathscr E^{(1)}\right]^2 \left[R^2 + T^2 -RT\left(\,e^{ik(L_3-L_4)} + e^{-ik(L_3-L_4)}\right)\right] \\ & = \left[\mathscr E^{(1)}\right]^2 \left(R^2 + T^2 \right)\left(1 - 2\frac{RT}{R^2+T^2}\cos(k\delta L)\right) \\ & = \left[\mathscr E^{(1)}\right]^2 \left(R^2 + T^2 \right)\left(1 - V\cos(k\delta L)\right) \\ \left\|\mathbf E_6^{(+)} | \mathbf 1 \rangle \right\|^2 & = \left[\mathscr E^{(1)}\right]^2 r^2t^2 \left(e^{ikL_3} + e^{ikL_4}\right) = \left[\mathscr E^{(1)}\right]^2 RT \left(e^{ikL_3} + e^{ikL_4}\right) \\ & = \left[\mathscr E^{(1)}\right]^2 RT \left[\left(\,e^{ik(L_3-L_4)} + e^{-ik(L_3-L_4)}\right)\right] \\ & = \left[\mathscr E^{(1)}\right]^2 2RT \left(\cos(k\delta L)\right) \\ & = \left[\mathscr E^{(1)}\right]^2 \left(R^2 + T^2 \right)\left(2\frac{RT}{R^2+T^2}\cos(k\delta L)\right) \\ & = \left[\mathscr E^{(1)}\right]^2 \left(R^2 + T^2 \right)\left(V\cos(k\delta L)\right) \end{aligned}
In a Mach-Zehnder interferometer, the probability of detecting a photon in either output depends on the path difference, similar to classical optics. This result holds for any interferometer or optical setup because the output field operators’ expressions as functions of the input operators mirror those of classical field amplitudes.
When a single photon is input, the resulting vacuum state factorizes. The factor multiplying the vacuum state matches the classical description, and the squared modulus yields the same interference pattern as classical calculations.