Multimode Quasi-Classical Radiation
A multimode quasi-classical state is a tensor product of quasi-classical states in different modes:
|\Psi_{qc} \rangle = | \alpha_1 \rangle \otimes | \alpha_2 \rangle \dots \otimes | \alpha_\lambda \rangle = \prod_\lambda | \alpha_\lambda \rangle
As a single mode evolves as e^{-i\omega_\lambda t} there is an immediate generalization:
|\Psi_{qc} \rangle(t) = \prod_\lambda | \alpha_\lambda e^{-i\omega t} \rangle Similarly, since [\mathbf a_i, \mathbf a_j] = \delta_{ij}, it is possible to generalize another result for a single mode as:
| \Psi_{qc} \rangle = e^{-\frac{\sum_\lambda|\alpha_\lambda|^2}{2}}e^{\sum_\lambda \alpha_\lambda \mathbf a_\lambda^\dag} | \mathbf 0 \rangle
The effect of the electric field are similar, and the multimode quasi-classical state is an eigenstate of the positive frequency of the electric field observable \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t), with the eigenvalue that has the form of the complex amplitude of the classical field. As in the single mode case, it is not an eigenstate of the total electric field.
Also the single and double detection rate are the same that would be obtain with a classical field:
\begin{aligned} & w^{(1)}(\mathbf{r}, t) = s \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t)\right|^2 \\ & w^{(2)}(\mathbf{r}_1, t_1, \mathbf{r}_2, t_2) = s^2 \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_1, t_1) \right|^2 \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_2, t_2) \right|^2 \end{aligned}
An underlying assumption to keep it compact in case of the double detection is to assume that the bandwidth is relatively narrow so that s is the same for all frequencies.
As in the single state, the multistate mode is not an eigenvalue of the number of photons observable. The average is just the sum of the photon numbers of the various modes:
\langle \mathbf N \rangle = \langle \Psi_{qc} | \mathbf N | \Psi_{qc} \rangle = \langle \Psi_{qc} | \sum_\lambda \mathbf a_\lambda^\dag \mathbf a_\lambda | \Psi_{qc} \rangle = \sum_\lambda \langle |\alpha_\lambda|^2 \rangle =\sum_\lambda \langle \mathbf N_\lambda \rangle
It is then possible to compute the variance, starting from the square of \mathbf N:
\begin{aligned} \langle \mathbf N^2 \rangle & = \langle \Psi_{qc} | \mathbf N^2 | \Psi_{qc} \rangle = \langle \Psi_{qc} | \left( \sum_\lambda \mathbf a_\lambda^\dag \mathbf a_\lambda \right)^2 | \Psi_{qc} \rangle\\ & = \langle \Psi_{qc} | \sum_{\lambda, \mu} \mathbf a_\lambda^\dag \mathbf a_\lambda \mathbf a_{\mu}^\dag \mathbf a_{\mu} | \Psi_{qc} \rangle \\ & = \langle \Psi_{qc} | \sum_{\lambda} \mathbf a_\lambda^\dag \mathbf a_\lambda \mathbf a_{\lambda}^\dag \mathbf a_{\lambda} | \Psi_{qc} \rangle \\ & = \langle \Psi_{qc} | \sum_{\lambda} \mathbf a^\dag \left(1 + \mathbf a^\dag \mathbf a \right) \mathbf a | \Psi_{qc} \rangle \\ & = \langle \Psi_{qc} | \sum_{\lambda} \left(\mathbf a^\dag \mathbf a \right)^2 | \Psi_{qc} \rangle + \langle \Psi_{qc} | \sum_{\lambda} \mathbf a^\dag \mathbf a | \Psi_{qc} \rangle \\ & = \langle \mathbf N \rangle ^2 + \langle \mathbf N \rangle \end{aligned}
Where we used the fact that [\mathbf a_i, \mathbf a_j] = \delta_{ij} so the cross terms are null. The variance is therefore:
\left(\Delta \mathbf N\right)^2 = \langle \mathbf N^2 \rangle - \langle \mathbf N \rangle ^2 = \langle \mathbf N \rangle ^2 + \langle \mathbf N \rangle - \langle \mathbf N \rangle ^2 = \langle \mathbf N \rangle
and the standard deviation is:
\Delta \mathbf N = \sqrt{\langle \mathbf N \rangle} = \sqrt{\langle \sum_\lambda \mathbf N_\lambda \rangle} = \sqrt{ \sum_\lambda \Delta \mathbf N_\lambda^2}
The latest formula suggests that the distribution of the photons follow a Poisson distribution.
Starting from defining the multimode creation operator as:
\mathbf a_{\text{multi}}^\dag \equiv \frac{1}{\alpha_{\text{multi}}}\sum_\lambda \alpha_\lambda \mathbf a_\lambda^\dag = \frac{1}{\sum_\lambda |\alpha_\lambda|^2 }\sum_\lambda \alpha_\lambda \mathbf a_\lambda^\dag = \frac{1}{\langle \mathbf N \rangle }\sum_\lambda \alpha_\lambda \mathbf a_\lambda^\dag
The multimode quasi-classical state can be then written as:
| \Psi_{qc} \rangle = e^{-\frac{\sum_\lambda|\alpha_\lambda|^2}{2}}e^{\sum_\lambda \alpha_\lambda \mathbf a_\lambda^\dag} | \mathbf 0 \rangle = e^{-\frac{|\alpha_{\text{multi}}|^2}{2}}e^{\alpha_{\text{multi}} \mathbf a_\lambda^\dag} | \mathbf 0 \rangle
This can be really considered a creation operator, as its Hermitian conjugate has the properties of a destruction operator, so that the standard properties apply:
\begin{aligned} &[\mathbf a_{\text{multi}}, \mathbf a_{\text{multi}}^\dag ] = 1\\ &\mathbf N_{\text{multi}} = \mathbf a_{\text{multi}}^\dag \mathbf a_{\text{multi}} \\ & [\mathbf N_{\text{multi}}, \mathbf a_{\text{multi}}^\dag] = \mathbf a_{\text{multi}}^\dag \\ & [\mathbf N_{\text{multi}}, \mathbf a_{\text{multi}}] = \mathbf a_{\text{multi}} \end{aligned}
All these operators are the same as \mathbf a_\lambda and \mathbf a^\dag for a mode \lambda.
The derivation of the eigenvalues of these operators are the same as in the case of the quantum harmonic oscillator, as the commutator relations are the same:
\begin{aligned} & \mathbf a_{\text{multi}} | \mathbf n \rangle = \sqrt {n_{\text{multi}}} | \mathbf {n_{\text{multi}} - 1} \rangle \\ & \mathbf a_{\text{multi}} | \mathbf 0 \rangle = 0 \\ & \mathbf a_{\text{multi}}^\dag | \mathbf n_{\text{multi}} \rangle = \sqrt {n_{\text{multi}} + 1} | \mathbf {n_{\text{multi}} + 1} \rangle \\ & \mathbf N_{\text{multi}} | \mathbf n_{\text{multi}} \rangle = \sum_\lambda \mathbf a^\dag_\lambda \mathbf a_\lambda | \mathbf n_{\text{multi}} \rangle = n_{\text{multi}} | \mathbf n_{\text{multi}} \rangle \\ & | \mathbf n_{\text{multi}} \rangle = \frac{\left(\mathbf a^\dag_{\text{multi}} \right)^{n_{\text{multi}}}}{\sqrt{n_{\text{multi}}!}}| \mathbf 0 \rangle \end{aligned}
with n \in \mathbb N.
It is now possible with this formalism as a basis to express multimode quasi-classical states:
| \Psi_{qc} \rangle = e^{-\frac{\langle \mathbf N \rangle}{2}}e^{\sum_\lambda \alpha_\lambda \mathbf a_\lambda^\dag} | \mathbf 0 \rangle = e^{-\frac{\langle \mathbf N \rangle}{2}} \sum \frac{\left(\mathbf a_{\text{multi}} \mathbf a^\dag_{\text{multi}} \right)^{n_{\text{multi}}}}{n_{\text{multi}!}}| \mathbf 0 \rangle
Using:
\left(\mathbf a_{\text{multi}}^\dag \right)^n_{\text{multi}} | \mathbf 0 \rangle = \sqrt {n_{\text{multi}}!} | \mathbf n_{\text{multi}} \rangle
then:
| \Psi_{qc} \rangle = e^{-\frac{\langle \mathbf N \rangle}{2}} \sum \frac{\left(\mathbf a_{\text{multi}} \right)^{n_{\text{multi}}}}{\sqrt{n_{\text{multi}!}}}| \mathbf n_{\text{multi}} \rangle
Computing the probability density (the square module of the coefficients) gives the probability of having a number n_{\text{multi}} of multimode photons:
P(n_{\text{multi}}) = e^{-\langle \mathbf N \rangle} \frac{\langle \mathbf N \rangle^{n_{\text{multi}}}}{n_{\text{multi}!}}
This is a Poisson distribution.
Collimated wavepackets
Let’s consider a beam propagating along x with a transverse surface S large enough that the diffraction is negligible on the length L.
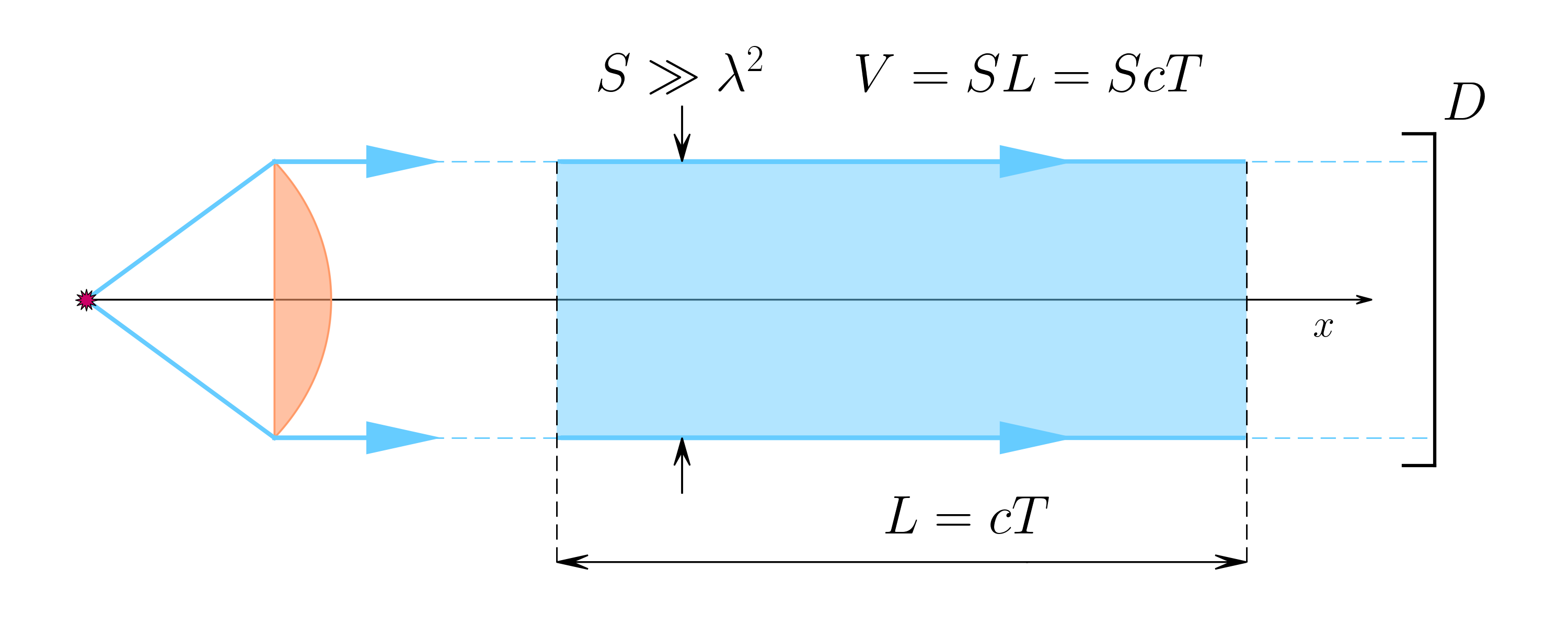
The modes are then plane waves propagating along x and linearly polarized in the y direction (\varepsilon_\lambda = \mathbf e_y =\varepsilon). It is possible to define modes taking periodic boundary conditions:
\mathbf k_\lambda = 2\pi \frac{n_\lambda}{L} \mathbf e_x =\frac{\omega_\lambda}{c}\mathbf e_x \quad n_\lambda \in \mathbb N
The wavefunction defining the wavepacket is a tensor product of modes spread around \omega_\lambda:
| \Psi_{\text{qcwp}} \rangle = \prod_\lambda | \alpha_\lambda e^{-i\omega_\lambda t} \rangle
We takes the coefficients defined here:
\alpha_\lambda = \frac{Ke^{i\omega_\lambda t_0}}{(\omega_\lambda - \omega_0) - i\frac{\Gamma}{2}}
with therefore the number of photons that assume a Lorentzian distribution. The sum of the square values is equal to the number values of photons:
\sum_\lambda |\alpha_\lambda|^2 = \sum_\lambda \frac{K^2}{(\omega_\lambda - \omega_0)^2 + \frac{\Gamma^2}{4}} = \langle \mathbf N \rangle
This condition will determine the value of K.
Replacing the sum with an integral and introducing the density of states, it is possible to compute the sum as:
\begin{aligned} & \sum_\lambda |\alpha_\lambda|^2 = \frac{K^2 L}{c \Gamma} = \langle \mathbf N \rangle \\ & K = \sqrt{\frac{c\Gamma}{L} \langle \mathbf N \rangle} \end{aligned}
The intrinsic quantities should not depends from the arbitrary length L, and they are not depending indeed; for example the electric field assume a classical form:
\begin{aligned} \langle \mathbf E \rangle (\mathbf r,t) & = \langle \Psi_{\text{qcwp}} (t) | \mathbf E (\mathbf r) | \Psi_{\text{qcwp}} \rangle \\ & =E ^{(+)}(\mathbf r,t) + E ^{(-)}(\mathbf r,t) = E_{\text{classical}}(\mathbf r,t) \\ & = \sum_\lambda i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \alpha_\lambda e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} \\ & = i \varepsilon \mathscr E^{(1)}_{\omega_0} \sum_\lambda \alpha_\lambda e^{i \omega_\lambda \left(t-\frac{z}{c}\right)} \\ & = \sqrt{\frac{\hbar \omega_0\Gamma}{2\varepsilon_0 cS} \langle \mathbf N \rangle} H(\tau)e^{-\frac{\Gamma}{2}\tau}e^{i\omega_0\tau} \end{aligned}
The calculation is similar to what done for the spontaneous emission case and it is an oscillation function multiplied for an envelop starting at \tau = t - t_0 - \frac{x}{c} and decaying exponentially.
The result is an intrinsic quantity as expected and does not depends from the arbitrary length L: the density of states scales as L while the constant K and the photon amplitude scales both as L^{-\frac{1}{2}}.
A photo-detector perpendicular to the direction of propagation allows to compute the probability of single detection at position x and time t, providing that the experiment is repeated many times; moreover the propagation delay \frac{x}{c} need to be taken into account.
For a quasi-classical state the photodetection rate is expressed as a function of the classical field:
w^{(1)}(\mathbf{r}, t) = s \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t)\right|^2 = s\frac{\hbar \omega_0\Gamma}{2\varepsilon_0 cS} \langle \mathbf N \rangle H(\tau)e^{-\Gamma\tau}
Defining the ideal sensitivity \eta as the one of an ideal photo-detector:
s = \eta\frac{2\varepsilon_0 c}{\hbar \omega_0}
Then the probability of detection takes the simple form:
w^{(1)}(\mathbf{r}, t) = \eta \frac{\Gamma}{S} \langle \mathbf N \rangle H(\tau)e^{-\Gamma\tau}
Since it is a quasi-classical state, the probability of double photo-detection is equal to the product of the single detection as in the classical case:
\begin{aligned} w^{(2)}(\mathbf{r}_1, t_1, \mathbf{r}_2, t_2) & = s^2 \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_1, t_1) \right|^2 \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_2, t_2) \right|^2 \\ & = w^{(1)}(\mathbf{r}_1, t_1) w^{(1)}(\mathbf{r}_2, t_2) \neq 0 \end{aligned}
This probability is not null (as in the single photon case) even if the average number of photon is small compared to one (\langle \mathbf N \rangle \ll 1), and intuitively we might think that it should be the case; it has been however demonstrated experimentally that this is not the case and the quantum optic computations are correct.
Beam splitter
Let’s consider a beam splitter, in which there are two input modes (1) and (2) and two output modes (3) and (4), with a unitary transformation \mathbf U which link the state | \Psi_{12} \rangle with |\Psi_{34} \rangle.
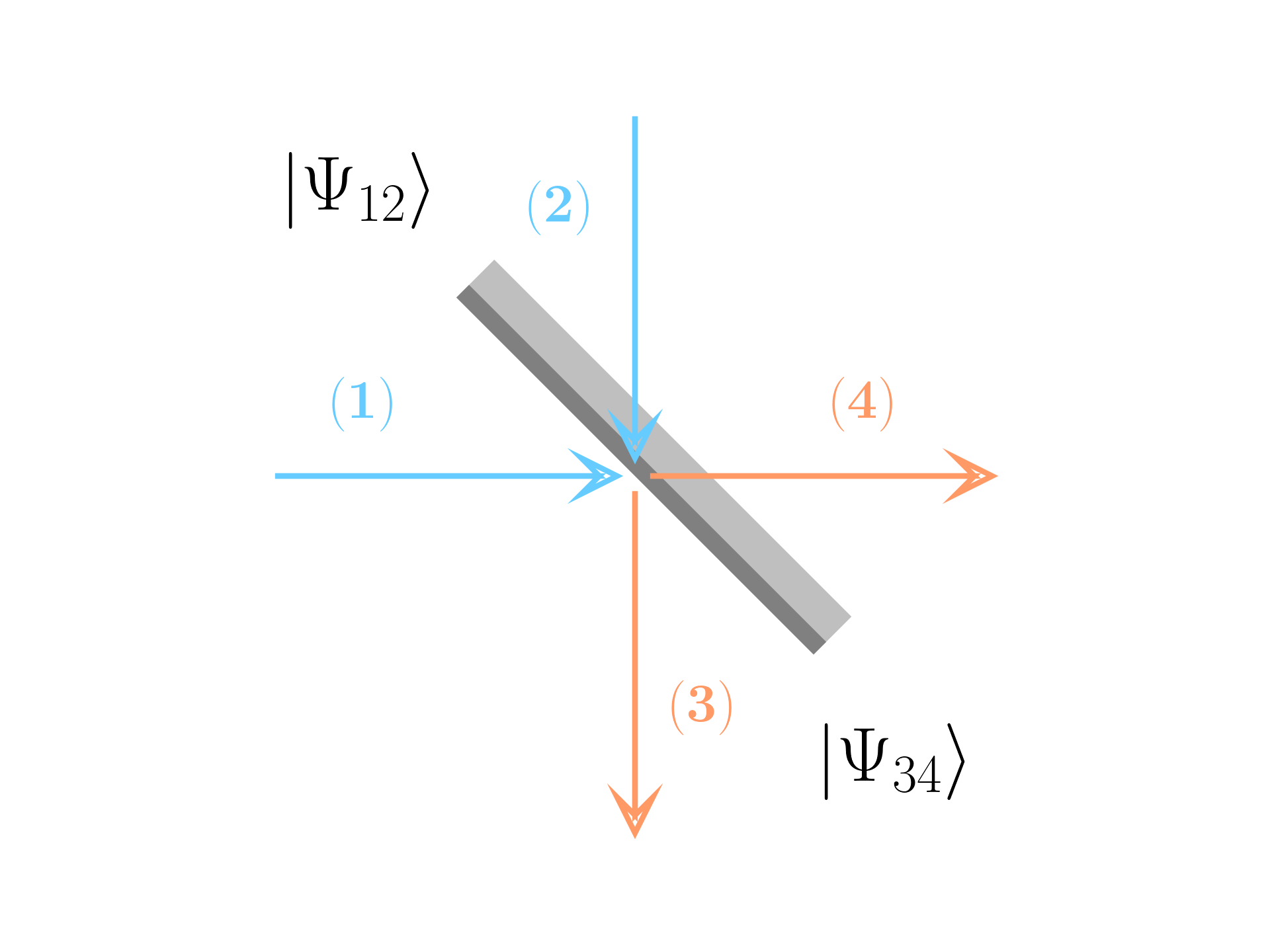
The objective is to calculate the the single and double detection in the output channel, the inputs are:
| \Psi_{12} \rangle = | \Psi_{\text{qcwp}} \rangle_1 (0) | \mathbf 0 \rangle_2 = \prod_\lambda | \alpha_\lambda \rangle_1 | \mathbf 0 \rangle_2
so there is a quasi-classical wavepacket in input (1) and the vacuum in input (2). As done for the single mode case, it is possible to express the results in the output space as function of the observables in the input space:
\begin{bmatrix} \mathbf E_3^{(+)} \\ \mathbf E_4^{(+)} \end{bmatrix} = \begin{bmatrix} r & t \\ t & -r \end{bmatrix} \begin{bmatrix} \mathbf E_1^{(+)} \\ \mathbf E_2^{(+)} \end{bmatrix}
The Heisenberg formalism is used, so it is sufficient to consider the wavefunction for t=0. The single photodetection, taking into account the propagation delay in the electric field is (using \tau =t - t_0 - \frac{z_3}{c} for the propagation delay:
\begin{aligned} w^{(1)}(\mathbf r_3,t) & = s \left\| \mathbf E_3^{(+)} (\tau) | \Psi_{34} \rangle (0) \right\|^2 \\ & = s \left\| r \mathbf E_1^{(+)} (\tau) | \Psi_{\text{qcwp}} (0) \rangle \right\|^2 \\ & = |r|^2 \eta \frac{\Gamma}{S}H \langle \mathbf N \rangle (\tau)e^{-\Gamma\tau} \end{aligned}
A similar calculation for (4) gives:
w^{(1)}(\mathbf r_4,t) = |t|^2 \eta \frac{\Gamma}{S}H \langle \mathbf N \rangle (\tau)e^{-\Gamma\tau}
Integrating this detection over the whole wave packet gives the average number of detected photons for each wavepacket:
\begin{aligned} P_3 & = \iiint w^{(1)}(\mathbf r_3,t) \mathrm dS \mathrm dt = |r|^2\eta \langle \mathbf N \rangle\\ P_4 & = \iiint w^{(1)}(\mathbf r_4,t) \mathrm dS \mathrm dt = |t|^2\eta \langle \mathbf N \rangle \end{aligned}
Since the double detection is the product of the single detection:
w^{(2)}(\mathbf{r}_3, t_3, \mathbf{r}_4, t_4) = w^{(1)}(\mathbf{r}_3, t_3) w^{(1)}(\mathbf{r}_4, t_4)
Integrating over the whole wavepacket, the integral split into two integral and the result is simply the product of the probabilities of each channel:
P_C = P_3 P_4
Therefore the probability of the double detection divided by the product of the probability of single detection is equal to one:
\frac{P_C}{P_3P_4} = \frac{P_3P_4}{P_3P_4} = 1
This results holds even if the number of photons in the wavepacket is small than one, and it has been proven experimentally. To explain this result, it is necessary to look into the distribution of the wavepacket and how it behaves. The distribution is a Poisson distribution:
P(\langle \mathbf N \rangle) = e^{-\langle \mathbf N \rangle} \frac{\langle \mathbf N \rangle^n}{n!}
Expanding to the first order if \langle \mathbf N \rangle \ll 1:
P(\langle \mathbf 1 \rangle) = e^{-\langle \mathbf N \rangle} \frac{\langle \mathbf N \rangle^1}{1!} = e^{-\langle \mathbf N \rangle} \langle \mathbf N \rangle \approx \left(1 - \langle \mathbf N \rangle\right)\langle \mathbf N \rangle = \langle \mathbf N \rangle - \langle \mathbf N \rangle^2 \approx \langle \mathbf N \rangle
The probability of being detected at (3) or (4) are t^2 and r^2 respectively; taking the quantum efficiency \eta they are:
\begin{aligned} P_3 & = |r|^2\eta \langle \mathbf N \rangle \\ P_4 & = |t|^2\eta \langle \mathbf N \rangle \end{aligned} which are identical to the ones calculated using the photodetection formulas.
The double detection is possible providing that there are two photons in the same wavepackets, and expanding to the lowest order:
P(\langle \mathbf 2 \rangle) = e^{-\langle \mathbf N \rangle} \frac{\langle \mathbf N \rangle^2}{2!} = e^{-\langle \mathbf N \rangle} \frac{\langle \mathbf N \rangle^2}{2} \approx \left(1 - \langle \mathbf N \rangle\right) \frac{\langle \mathbf N \rangle^2}{2} = \frac{\langle \mathbf N \rangle^2}{2} - \frac{\langle \mathbf N \rangle^3}{2} \approx \frac{\langle \mathbf N \rangle^2}{2}
Assuming that the pair of photons are redistributed randomly and independently in the output of the beam splitter, the probabilities to find it there are:
\begin{aligned} & P_{33} = |r|^4 \\ & P_{44} = |t|^4 \\ & P_{34} = 2|r|^2|t|^2 \end{aligned}
The probability of find one photon in each channel is doubled than the one to find them in the same channel, as there are two different ways to distribute two independent particles in these channels. Introducing the efficiency \eta the probability of joint detection is:
P_C = \eta 2|r|^2|t|^2 \frac{\langle \mathbf N \rangle^2}{2} = \eta |r|^2|t|^2 \langle \mathbf N \rangle = P_3 P_4
The same result can be computed using the quantum optics formalism.
Let’s consider the same beam splitter, but now the input state a two photons state in input (1) and the vacuum in input (2):
| \Psi_{12} \rangle = | \mathbf 2 \rangle_1 | \mathbf 0 \rangle_2 = \frac{\left(\mathbf a_1^\dag\right)^2}{\sqrt 2} | \mathbf 0 \rangle
then the creation operator in channel (1) can be replaced with the correspondent operators of output (3) and (4):
\mathbf a_1^\dag = r \mathbf a_3^\dag + t \mathbf a_4^\dag
and therefore:
\begin{aligned} | \Psi_{34} \rangle & = \frac{\left(r \mathbf a_3^\dag + t \mathbf a_4^\dag \right)^2}{\sqrt 2} | \mathbf 0 \rangle \\ & = \frac{r^2 \left(\mathbf a_3^\dag\right)^2 + 2rt \mathbf a_3^\dag r \mathbf a_4^\dag + t^2 \left(\mathbf a_4^\dag\right)^2}{\sqrt 2} | \mathbf 0 \rangle \\ & = r^2 | \mathbf 2 \rangle_3 + t^2 | \mathbf 2 \rangle_4 + \sqrt 2 rt | \mathbf 1 \rangle_3 | \mathbf 1 \rangle_4 \end{aligned}
The square moduli of the coefficients gives the probabilities of the various outcome:
\begin{aligned} & P_{33} = |r|^4 \\ & P_{44} = |t|^4 \\ & P_{34} = 2|r|^2|t|^2 \end{aligned}
The factor of two in the last case arises from the fact that there are two different ways to put one photon in one channel and one in the other, so the particles behave as if they were independent from each other.
So two photons in the same mode don’t tend to be found preferably in the same output channel, as one might have expected since photons are bosons; the results above coming from quantum optics and has been also experimentally verified.