Spontaneous Emission One Photon
In free space, radiation is emitted in all directions, and describing the emitted radiation requires modes of the electromagnetic field that are well-suited to this geometry.
Let’s consider a scenario where the emitter is at the focus of a deep parabolic mirror with transverse dimensions much larger than the wavelength. This allows us to expand the resulting one-photon state in a basis of plane waves with \mathbf k_\lambda vectors along the z-axis. The discrete values of \mathbf k_\lambda are set by a periodic boundary condition along z with a length L, which can be arbitrarily large. We associate a duration T with this length L. The quantization volume is the product of the transverse surface S and L. As usual, the final results relevant to experimental quantities should not depend on L.
For simplicity, we will only consider one polarization perpendicular to the z-axis, for instance, along the x-axis. Thus, the index \lambda corresponds to the integer n_\lambda:
\mathbf k_\lambda = 2\pi\frac{n_\lambda}{L}\mathbf e_z = \frac{\omega_\lambda}{c}\mathbf e_z,\quad n_\lambda \in \mathbb N
A one photon packet resulting from spontaneous emission is described by:
\begin{aligned} & | \psi(t_0) \rangle = | \mathbf 1 \rangle = \sum_\lambda c_\lambda | \mathbf 1_\lambda \rangle \\ & c_\lambda = \frac{Ke^{i\omega_\lambda t_0}}{(\omega_\lambda - \omega_0) - i\frac{\Gamma}{2}} \end{aligned}
Where K is a normalization constant and \frac{1}{\Gamma} is the lifetime of the excited state of the atom (after that time there is the certainty that one photon has been emitted).
The square modulus of the coefficient c_\lambda gives the spectrum distribution which is the spectrum of the radiation:
\left|c_\lambda\right|^2 = \frac{K^2}{(\omega_\lambda - \omega_0)^2 + \frac{\Gamma^2}{4}}
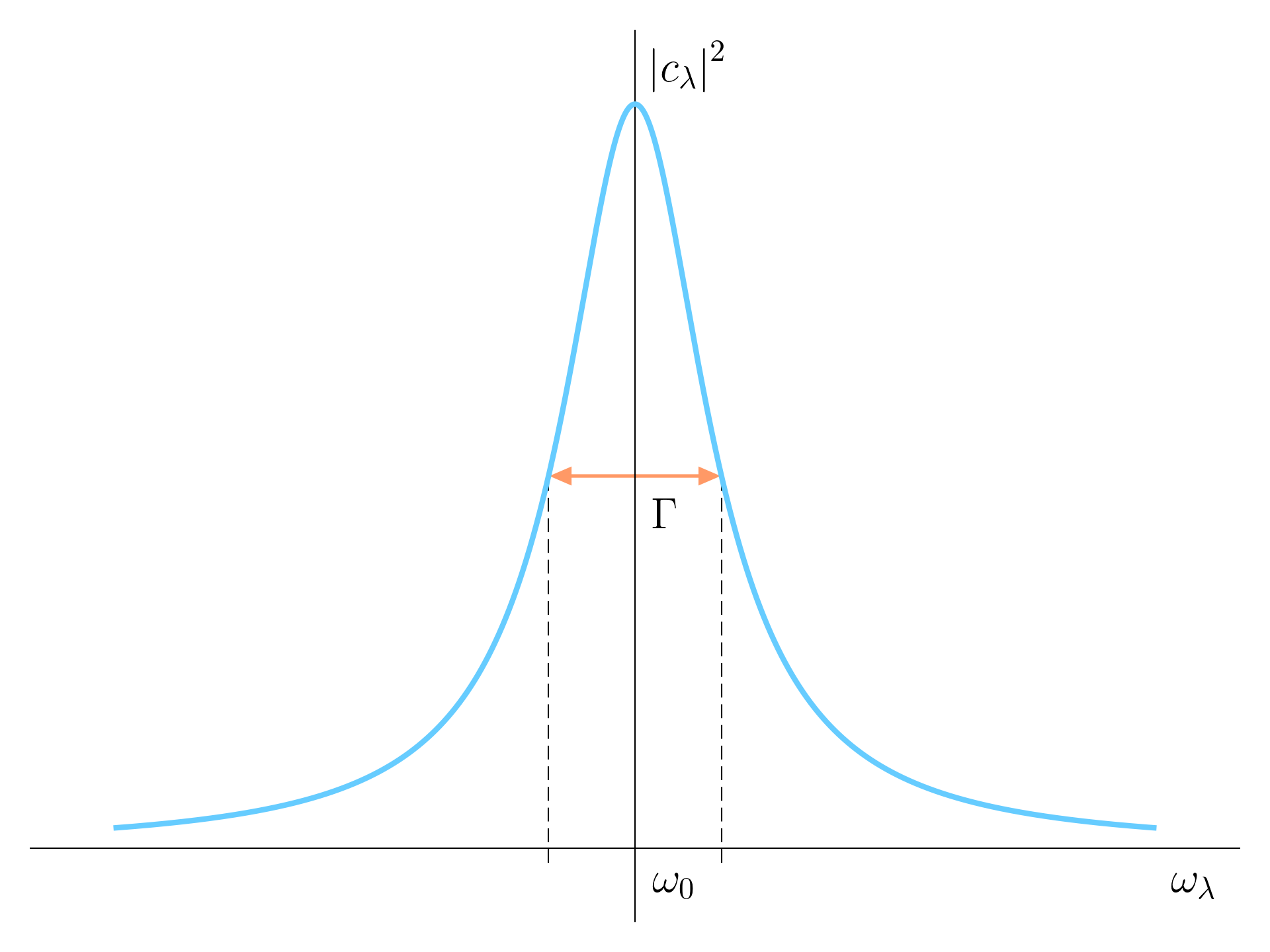
This distribution is a Lorentzian, which has an half width half maximum \frac{\Gamma}{2}.
Normalization
To complete the calculation, it is necessary to determine the value of the coefficient K which normalize the expression:
\sum_\lambda \left|c_\lambda\right|^2 = 1
To perform this calculation, the first step is to replace the sum with an integral:
\sum_\lambda \left|c_\lambda\right|^2 = \int_{-\infty}^{\infty}\frac{K^2}{(\omega_\lambda - \omega_0)^2 + \frac{\Gamma^2}{4}}\frac{\mathrm dn_\lambda}{\mathrm d\omega_\lambda}\mathrm d\omega_\lambda
where:
\frac{\mathrm dn_\lambda}{\mathrm d\omega_\lambda}\mathrm d\omega_\lambda
is the density of modes in \mathrm d\omega_\lambda. In this case it can be derived from the periodic boundary conditions:
\frac{\mathrm dn_\lambda}{\mathrm d\omega_\lambda}\mathrm d\omega_\lambda = \frac{L}{2\pi c}\mathrm d\omega_\lambda
Substituting this value:
\sum_\lambda \left|c_\lambda\right|^2 = \int_{-\infty}^{\infty}\frac{K^2}{(\omega_\lambda - \omega_0)^2 + \frac{\Gamma^2}{4}}\frac{L}{2\pi c}\mathrm d\omega_\lambda
The integral we are considering has the form:
\int_{-\infty}^{\infty} \frac{A}{(x - x_0)^2 + B^2} \, dx
This integral is a standard result in mathematical analysis and is related to the Cauchy principal value of the integral of a Lorentzian function, also known as a Breit-Wigner distribution.
The specific result we are using is:
\int_{-\infty}^{\infty} \frac{A}{(x - x_0)^2 + B^2} \, dx = \frac{\pi A}{B}
The derivation of this result can be understood using the residue theorem. Here’s a sketch of the derivation:
-
Integral Setup: Consider the function f(z) = \frac{A}{(z - x_0)^2 + B^2}, where z is a complex variable. This function has poles (singularities) at z = x_0 + iB and z = x_0 - iB.
-
Contour Integration: To evaluate the integral, we considers a semicircular contour in the complex plane that extends into the upper or lower half-plane, enclosing one of the poles.
-
Residue Theorem: Using the residue theorem, which states that the integral of a function around a closed contour is 2\pi i times the sum of residues of the enclosed poles, we evaluate the integral. The residue at z = x_0 + iB is:
\text{Res}\left( f(z), z = x_0 + iB \right) = \lim_{z \to x_0 + iB} (z - (x_0 + iB)) \frac{A}{(z - x_0)^2 + B^2} = \frac{A}{2iB}
- Applying the Residue Theorem: When integrating around a contour that encloses z = x_0 + iB, the integral is:
\int_{\text{contour}} f(z) \, dz = 2\pi i \cdot \frac{A}{2iB} = \frac{\pi A}{B}
Since the integral over the semicircular part of the contour vanishes as its radius goes to infinity, the integral over the real line remains:
\int_{-\infty}^{\infty} \frac{A}{(x - x_0)^2 + B^2} \, dx = \frac{\pi A}{B}
Identifying:
- A = K^2 \frac{L}{2\pi c}
- x = \omega_\lambda
- x_0 = \omega_0
- B = \frac{\Gamma}{2}
Plugging these into the known formula:
\int_{-\infty}^{\infty}\frac{K^2}{(\omega_\lambda - \omega_0)^2 + \frac{\Gamma^2}{4}}\frac{L}{2\pi c}\mathrm{d}\omega_\lambda = \frac{\pi \left( K^2 \frac{L}{2\pi c} \right)}{\frac{\Gamma}{2}} = \frac{K^2 L}{c \Gamma}
So the result of the integral is:
\frac{K^2 L}{c \Gamma}
Therefore:
\left|c_\lambda\right|^2 = \frac{K^2 L}{c \Gamma} = 1 \quad \Rightarrow \quad K = \sqrt{\frac{c\Gamma}{L}}
Photodetection
Let us now calculate the rate of single photodetection at time t, given that our emitter was excited at time t_0. This corresponds to measurements taken using a photodetector positioned at z and a device to measure the delay t - t_0. Each measurement will yield a single value. However, by repeating the experiment multiple times, we can construct a histogram showing the probability of detecting a count at each delay value. This histogram represents the photodetection rate as a function of t - t_0.
Considering the expression of w^{(1)} in the Heisenberg formalism:
\begin{aligned} w^{(1)}(\mathbf r,t) & = s \left\|\mathbf{E}^{(+)}(\mathbf{r}, t) | \psi(t_0) \rangle \right\|^2 \\ & = s \left\|\sum_\lambda \mathbf{e}_\lambda c_\lambda \mathscr E^{(1)}_\lambda e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} \mathbf a_\lambda | \mathbf 1_\lambda \rangle \right\|^2 \\ & = s \left\|\mathbf{e}_\lambda \sum_\lambda c_\lambda \mathscr E^{(1)}_\lambda e^{-i\omega_\lambda \left(t- \frac{z}{c}\right)} | \mathbf 0\rangle \right\|^2 \end{aligned}
before proceeding, we replace \mathscr E^{(1)}_\lambda with it value around \omega_0:
\mathscr E^{(1)}_\lambda = \sqrt{\left(\frac{\hbar \omega_\lambda}{2\varepsilon_0 S L}\right)} \approx \mathscr E^{(1)}_{\omega_0} = \sqrt{\left(\frac{\hbar \omega_0}{2\varepsilon_0 S L}\right)}
Experimentally, it is found that this quantity is almost constant around \omega_0 for a bandwidth of a few \Gamma. Then it is possible again to replace the sum with an integral:
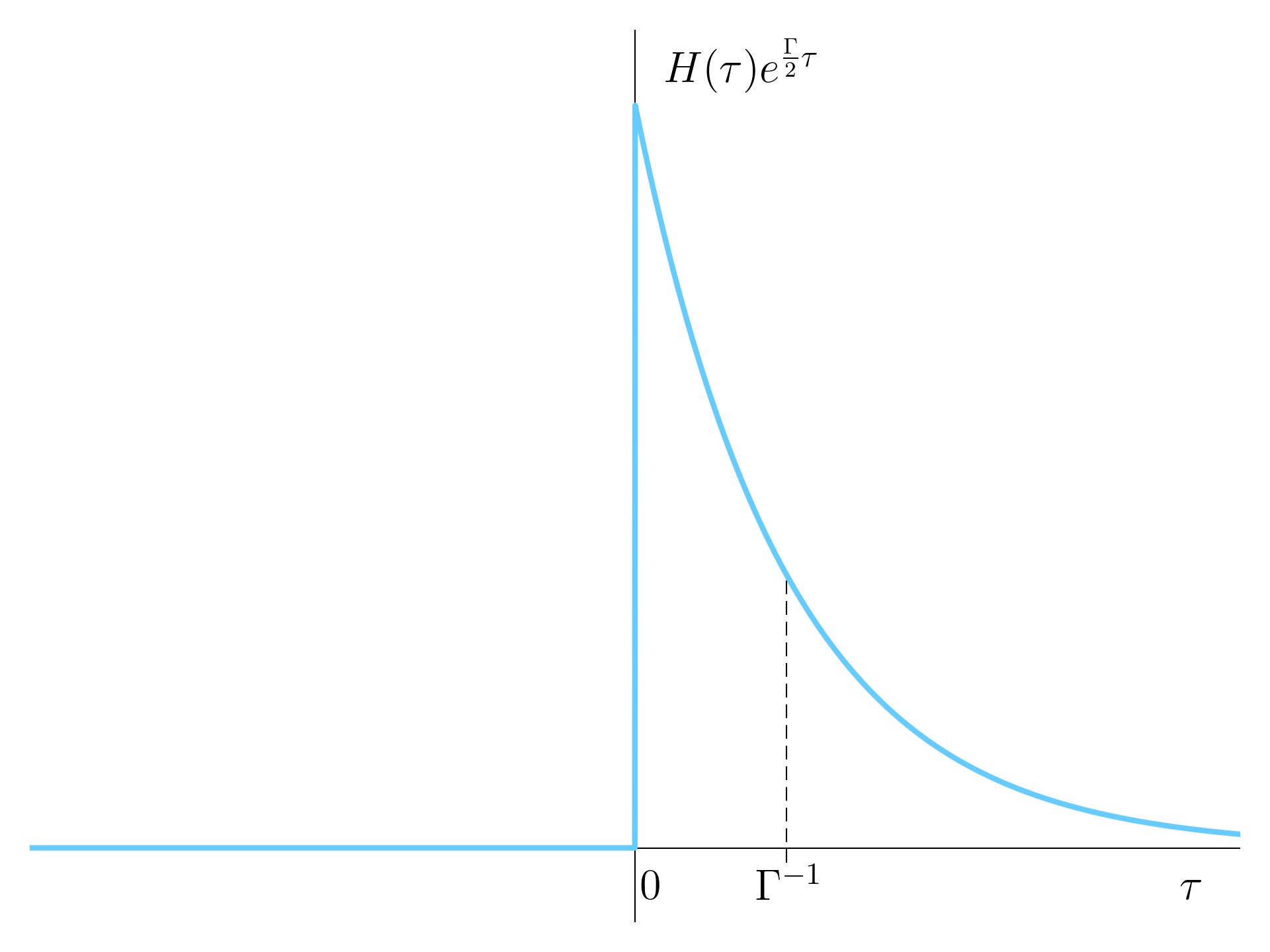
\begin{aligned} w^{(1)}(\mathbf r,t) & = s \left\|\mathbf{e}_\lambda \sum_\lambda c_\lambda \mathscr E^{(1)}_\lambda e^{-i\omega_\lambda \left(t- \frac{z}{c}\right)} | \mathbf 0\rangle \right\|^2 \\ & = s \left\|\mathbf{e}_\lambda \mathscr E^{(1)}_{\omega_0} \sum_\lambda c_\lambda e^{-i\omega_\lambda \left(t- \frac{z}{c}\right)} | \mathbf 0\rangle \right\|^2 \\ & = s \left\|\mathbf{e}_\lambda \mathscr E^{(1)}_{\omega_0} \left(\int_{-\infty}^{\infty}\frac{e^{-i\omega_\lambda \left(t-t_0 -\frac{z}{c}\right)}}{(\omega_\lambda - \omega_0) + \frac{i\Gamma}{2}}\sqrt{\frac{c\Gamma}{L}}\frac{L}{2\pi c}\mathrm d\omega_\lambda \right) | \mathbf 0\rangle \right\|^2 \\ & = s \left\|\mathbf{e}_\lambda \mathscr E^{(1)}_{\omega_0} \left(\sqrt{\frac{c\Gamma}{L}}\frac{L}{2\pi c} e^{-i\omega_0 \left(t- \frac{z}{c}\right)} \int_{-\infty}^{\infty}\frac{e^{-i(\omega_\lambda - \omega_0)\left(t - t_0 - \frac{z}{c}\right)}}{(\omega_\lambda - \omega_0) + \frac{i\Gamma}{2}}\mathrm d\omega_\lambda \right) | \mathbf 0\rangle \right\|^2 \\ & = s \left\|\mathbf{e}_\lambda \mathscr E^{(1)}_{\omega_0} \left(-i\sqrt{\frac{c\Gamma}{L}}\frac{L}{2\pi c} H(\tau)e^{-\left(i\omega_0 + \frac{\Gamma}{2}\right)\tau}\right) | \mathbf 0\rangle \right\|^2 \\ & = s \left[\mathscr E^{(1)}_{\omega_0}\right]^2 \frac{L\Gamma}{c}H(\tau)e^{-\Gamma\tau} \end{aligned}
where a known Fourier transform has been used:
\int \frac{e^{-ix\tau}}{x + i\frac{\Gamma}{2}} = -2\pi i H(\tau)e^{-\frac{\Gamma}{2}\tau}
with H(\tau) the Heaviside or step function, and \tau = t - t_0 - \frac{z}{c}.
Replacing the value of \mathscr E^{(1)}_{\omega_0} we get the single rate of photodection:
w^{(1)}(\mathbf r,t) = s \left[\mathscr E^{(1)}_{\omega_0}\right]^2 \frac{L\Gamma}{c}H(\tau)e^{-\Gamma\tau} = s \frac{\hbar \omega_0}{2\varepsilon_0 S} \frac{\Gamma}{c}H(\tau)e^{-\Gamma\tau} = \eta \frac{\Gamma}{c}H(\tau)e^{-\Gamma\tau}
which is not dependent from L and using the definition of the quantum efficiency \eta.
At time t_0, the emitter is excited, and at time t, we register a photodetection event on a detector located at a distance z from the emitter. A monitoring device using a time-to-digital converter allows us to obtain the delay between the excitation time t_0 and the detection time t. By repeating this many times, the apparatus builds a histogram of the delays and the number n of such measurements increases the histogram approaches w^{(1)} of t at position z.
The rising step of the exponential occurs at t = t_0 + \frac{z}{c}, corresponding to the excitation time plus a delay due to the propagation from the emitter to the detector.