Freely Propagating Beam
Let’s consider a freely propagating beam of transverse area S, which can be classically described as a plain wave with a constant electric field in the section of the beam:
\mathbf{E}(\mathbf{r}, t) = i\mathbf{e}_\lambda E_\lambda(0) \left(e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} + e^{-(i\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} \right)
The amplitude on this electric field is a well defined quantity, with an intrinsic meaning.
The are other intrinsic quantities, like the irradiance, which is the power per unit surface and equal to the modulus of the Poynting vector:
\Pi = 2\varepsilon_0 c |E_\lambda(0)|^2
The density of energy per unit volume:
D = 2\varepsilon_0 |E_\lambda(0)|^2 = \frac{\Pi}{c}
The total power flowing across any section of the beam:
\Phi = \Pi S
This can be measured for example with a power meter covering the whole transverse section of the beam.
Dividing this quantity by \hbar \omega_\lambda we can compute the photon flux:
\Phi_{\text{photon}} = \frac{\Phi}{\hbar \omega_\lambda}
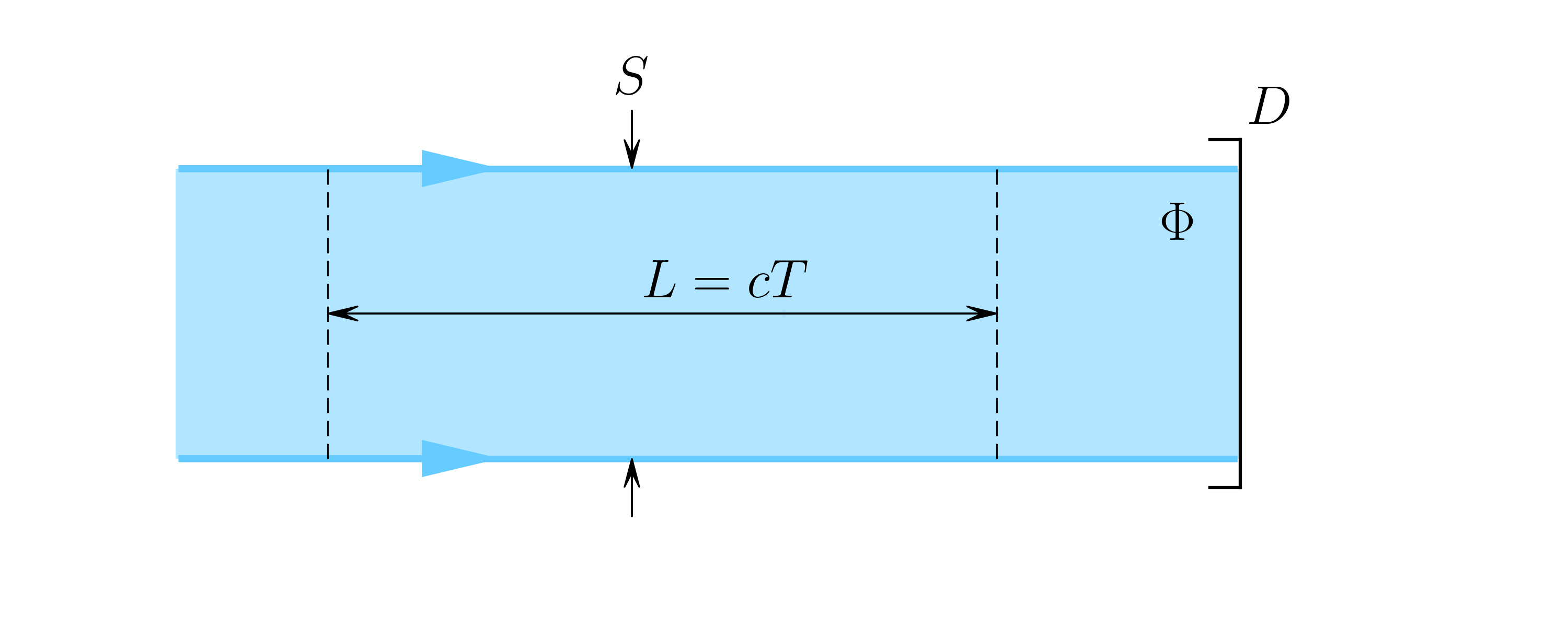
It is possible to look for similar quantities in the quantum formalism; but to do so it is necessary to have a quantization volume, it is possible then to define an arbitrary volume, which is a portion of beam with an arbitrary length L = cT, on which the length is replace by arbitrary time multiplied by the speed of light, the volume is then:
V_\lambda = S c T
The number of photon is not an intrinsic quantity, but the quantum flux of photon:
\Phi_{\text{photon}} =\frac{\mathbf N_\lambda}{T}
The average is:
\langle \alpha_\lambda | \Phi_{\text{photon}} | \alpha_\lambda \rangle =\frac{\langle \alpha_\lambda | \mathbf N_\lambda| \alpha_\lambda \rangle }{T} = \frac{|\alpha_\lambda|^2}{T}
Stating that this should be equal to the classical quantity gives:
\frac{|\alpha_\lambda|^2}{T} = \frac{\Phi}{\hbar \omega_\lambda}
and therefore it is an intrinsic quantity; while it depends from T, also \alpha_\lambda has a dependency so when the quantity it is computed it cancel out. Computing as example the average of the electric field:
\langle \alpha_\lambda | \mathbf{E}(\mathbf{r}, t) | \alpha_\lambda \rangle = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\alpha_\lambda e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} + \bar \alpha_\lambda e^{-(i\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} \right)
And remembering the one photon amplitude:
\mathscr E^{(1)}_\lambda = \sqrt{\frac{\hbar \omega_\lambda}{2\varepsilon_0 V_\lambda}} = \sqrt{\frac{\hbar \omega_\lambda}{2\varepsilon_0 S c T}} So the average becomes:
\begin{aligned} \langle \alpha_\lambda | \mathbf{E}(\mathbf{r}, t) | \alpha_\lambda \rangle & = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\alpha_\lambda e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} + \bar \alpha_\lambda e^{-(i\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} \right) \\ & = i\mathbf{e}_\lambda \sqrt{\frac{\hbar \omega_\lambda}{2\varepsilon_0 S c T}} \left(\sqrt{\frac{\Phi T}{\hbar \omega_\lambda}} e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} + \sqrt{\frac{\Phi T}{\hbar \omega_\lambda}} e^{-(i\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} \right) \\ & = i\mathbf{e}_\lambda \sqrt{\frac{\Phi}{2\varepsilon_0 S c}} \left(e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} + e^{-(i\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} \right) \\ \end{aligned}
Which is no longer dependent from the arbitrary time T. So, in order to describe a quasi-classical state in the quantum formalism it is necessary to use the parameter \alpha_\lambda which is proportional to the inverse of the square root of the arbitrary time T, which is chosen to agree with the photon flux.
The shot noise is the quantum fluctuation that can be measured on photodetection measurements on a perfectly stable beam and are responsible for the limited accuracy in measurements.
For an ideal photodetector which produces one pulse for each photon, the photon current observed in an integration time T is:
i_T = q_e \frac{N(T)}{T}
It is now possible to evaluate the fluctuations of a beam with intensity \Phi, assuming that the beam is a semi-classical state with a parameter |\alpha_{\lambda,T}| that was previously calculated and the state is written as:
|\psi \rangle = | \alpha_{\lambda,T} \rangle
to highlight that the quantity depends from the interval T. The number of count and the variance is the number of photon and the variance associated with the quantization volume of length cT:
N (T) = \langle \alpha_{\lambda,T}| \mathbf N_\lambda| \alpha_{\lambda,T} \rangle = |\alpha_{\lambda,T}|^2 = \frac{\Phi}{\hbar \omega_\lambda} T
For the variance, since it is a semi-classical state, the results were previously calculated (here) and it is equal to the number of photons:
\left[ \Delta N (T) \right]^2 = \langle \alpha_{\lambda,T}| \mathbf N_\lambda^2 | \alpha_{\lambda,T} \rangle - \left(\langle \alpha_{\lambda,T}| \mathbf N_\lambda| \alpha_{\lambda,T} \rangle\right)^2 = \langle \alpha_{\lambda,T}| \mathbf N_\lambda| \alpha_{\lambda,T} \rangle = \frac{\Phi}{\hbar \omega_\lambda} T
The standard deviation scales as \sqrt{T}:
\Delta N (T) = \sqrt{ \frac{\Phi}{\hbar \omega_\lambda} T }
The accuracy is then the ratio between the number of photon measured and the standard deviation:
\frac{N(T)}{\Delta N(T)} = \sqrt{ \frac{\Phi}{\hbar \omega_\lambda} T } = \sqrt{\Phi_{\text{photon}}T}
So the accuracy is proportional to the square root of the duration measurement T; it also increased with the power of the beam, because there are more photon per unit time.
Average photocurrent
For an ideal photodetector which produces one pulse for each photon, the photon current observed in an integration time T is:
\mathbf i_T = q_e \frac{\mathbf N(T)}{T}
Computing the average current:
\langle \mathbf i_T \rangle = q_e \frac{\langle \mathbf N(T) \rangle}{T} = q_e \frac{\Phi}{\hbar \omega_\lambda} = q_e \Phi_{\text{photon}} = \langle \mathbf i \rangle
which is an intrinsic quantity as it no longer depends from T.
If the detector is not ideal, then there is a factor \eta (the quantum efficiency of the detector) that should be then considered:
\langle \mathbf i_T \rangle = \eta q_e \frac{\langle \mathbf N(T) \rangle}{T} = \eta q_e \frac{\Phi}{\hbar \omega_\lambda} = \eta q_e \Phi_{\text{photon}} = \langle \mathbf i \rangle
The maximum value of \eta is 1 in case of an ideal detector.
Since the current is proportional to the number of photons, the standard deviation is:
\Delta \mathbf i = \frac{q_e}{T} \Delta \mathbf N (T) = \frac{q_e}{T} \sqrt{ \frac{\Phi}{\hbar \omega_\lambda} T } = q_e \sqrt{ \frac{\Phi}{\hbar \omega_\lambda T}}
Considering a typical electric circuit, which has a filtering described by:
\Delta \omega \propto \frac{2\pi}{T}
and using two single side bandwidth (which are restricted only to positive frequencies), transforming into frequency:
\frac{2\pi}{T} = 2 \Delta \omega_{1/2} = 4 \pi \Delta f_{1/2}
retrieving T^{-1}:
\frac{1}{T} = 2 \Delta f_{1/2}
which gives the shot noise formula:
\Delta \mathbf i = q_e \sqrt{ \frac{\Phi}{\hbar \omega_\lambda}2 \Delta f_{1/2}} = \sqrt{2 q_e \langle \mathbf i \rangle \Delta f_{1/2}}
This formula is not changed for a non-ideal detector as the parameter \eta is incorporated already in the average current.
This is true for every frequency bandwidth, so the index 1/2 can be dropped:
\Delta \mathbf i= \sqrt{2 q_e \langle \mathbf i \rangle \Delta f} = \Delta \mathbf i_{\Delta f}
The power spectral density of the photocurrent is defined as:
S_i = \frac{\left(\Delta \mathbf i_{\Delta f} \right)^2}{\Delta f}
The power contained between two frequencies f_1 and f_2 is the integral of this quantity:
\mathbf i_2 - \mathbf i_1 = \int_{f_1}^{f_2} S_i(f) \mathrm df
For the shot noise, the power spectral density is constant:
S_i(f) = 2 q_e \langle \mathbf i \rangle = \text{constant}
This is the white noise.
This formula has been known for some time and can be demonstrated in the framework of the semi-classical description, consider a Poisson process an a constant probability of emission of an electron.