Coherent State
Derivation
A quasi-classical states (or Glauber coherent state) is defined by the state vector:
| \alpha_\lambda \rangle = e^{-\frac{|\alpha_\lambda|^2}{2}} \sum_{n_\lambda = 0}^\infty \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} | \mathbf n_\lambda \rangle
were \alpha_\lambda = |\alpha|e^{i\phi} is a complex number. This state is an eigenstate of the annihilation operator:
\begin{aligned} \mathbf a_\lambda | \alpha_\lambda \rangle & = \mathbf a_\lambda e^{-\frac{|\alpha_\lambda|^2}{2}} \sum_{n_\lambda = 0}^\infty \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} | \mathbf n_\lambda \rangle \\ & = e^{-\frac{|\alpha_\lambda|^2}{2}}\sum_{n_\lambda = 0}^\infty \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} \sqrt{n_\lambda} | \mathbf n_\lambda - 1 \rangle \\ & = \alpha_\lambda e^{-\frac{|\alpha_\lambda|^2}{2}}\sum_{n_\lambda = 0}^\infty \frac{\alpha_\lambda^{n-1}}{\sqrt{(n_\lambda-1)!}} | \mathbf n_\lambda - 1 \rangle \\ & = \alpha_\lambda e^{-\frac{|\alpha_\lambda|^2}{2}}\left( 0 + \sum_{n_\lambda = 1}^\infty \frac{\alpha_\lambda^{n-1}}{\sqrt{(n_\lambda-1)!}} | \mathbf n_\lambda - 1 \rangle \right) \\ & = \alpha_\lambda e^{-\frac{|\alpha_\lambda|^2}{2}}\sum_{n_\lambda = 0}^\infty \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} | \mathbf n_\lambda \rangle \\ & = \alpha_\lambda | \alpha_\lambda \rangle \end{aligned}
obtained using the relation:
\mathbf a_\lambda | \mathbf n_\lambda \rangle = \sqrt{n_\lambda -1} | \mathbf n_\lambda - 1 \rangle
Given the electric field expression:
\mathbf E (\mathbf r) = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right)
It is possible to compute the average value:
\begin{aligned} \langle \alpha_\lambda | \mathbf E (\mathbf r) | \alpha_\lambda \rangle & = \langle \alpha_\lambda|i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) | \alpha_\lambda\rangle \\ & = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\langle \alpha_\lambda| \left(\mathbf a_\lambda | \alpha_\lambda\rangle \right) e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \left(\langle \alpha_\lambda| \mathbf a_\lambda^\dag\right) | \alpha_\lambda\rangle e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \\ & = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\alpha_\lambda\langle \alpha_\lambda| \alpha_\lambda\rangle e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \bar\alpha_\lambda\langle \alpha_\lambda | \alpha_\lambda \rangle e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \\ & = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\alpha_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r}} - \bar\alpha_\lambda e^{-i\mathbf{k}_\lambda \cdot \mathbf{r}} \right) \end{aligned}
Using the Schrödinger formulation, it is possible to compute the time dependent average of the electric field:
\begin{aligned} \langle \mathbf E \rangle (\mathbf r,t) & = \langle \psi (t) | \mathbf E (\mathbf r) | \psi(t) \rangle = \langle \alpha_\lambda e^{i\omega_\lambda t} | \mathbf E (\mathbf r) | \alpha_\lambda e^{-i \omega_\lambda t}\rangle \\ & = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\alpha_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r} -\omega_\lambda t} - \bar \alpha_\lambda e^{-i\mathbf{k}_\lambda \cdot \mathbf{r} + \omega_\lambda t} \right) \\ & =E ^{(+)}(\mathbf r,t) + E ^{(-)}(\mathbf r,t) = E_{\text{classical}}(\mathbf r,t) \end{aligned}
This is a form identical to the form of a classical field of the mode \lambda.
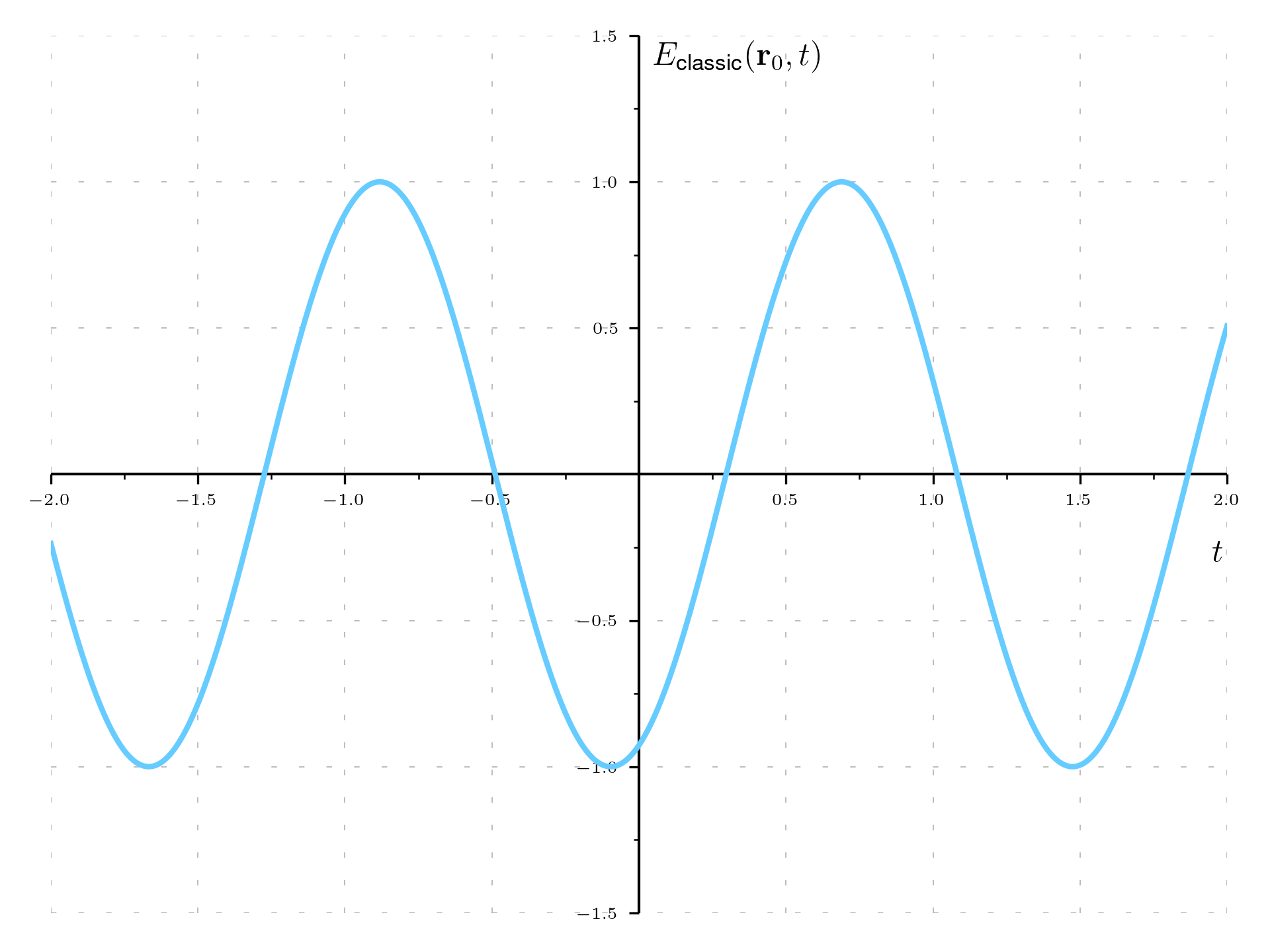
The spatial temporal dependence of the average value of the field is exactly the same as for a classical field. This is in contrast with the case of a number state for the same mode \lambda, which does not evolve neither in space nor in time, because it is an eigenvalue of the number operator \mathbf N and consequently of the Hamiltonian \mathbf H and as such does not evolve with time.
However, this average value is not sufficient to characterize the quantum mechanics properties of the electric field, as it is necessary to compute the standard deviation as well and apply Heisenberg uncertainty principle.
To calculate the variance, once the mean is known, it is sufficient to calculate the average of the square and subtract it from the square of the average. It is possible to start from t=0.
\begin{aligned} \langle \left[ \mathbf E \right]^2 \rangle (\mathbf r,0) & = \langle \psi (0) | \left[ \mathbf E (\mathbf r) \right]^2 | \psi(0) \rangle = \langle \alpha_\lambda | \left[ \mathbf E (\mathbf r) \right]^2 | \alpha_\lambda \rangle \\ & = - \left[\mathscr E^{(1)}_\lambda\right]^2 \langle \alpha_\lambda | \left(\mathbf a_\lambda - \mathbf a_\lambda^\dag\right)^2 | \alpha_\lambda \rangle \\ & = - \left[\mathscr E^{(1)}_\lambda\right]^2 \langle \alpha_\lambda | \left(\mathbf a_\lambda^2 - \mathbf a_\lambda\mathbf a_\lambda^\dag - \mathbf a_\lambda^\dag\mathbf a_\lambda +\left(\mathbf a_\lambda^\dag\right)^2\right) | \alpha_\lambda \rangle \\ & = - \left[\mathscr E^{(1)}_\lambda\right]^2 \langle \alpha_\lambda | \left(\mathbf a_\lambda^2 + 1 - 2 \mathbf a_\lambda^\dag \mathbf a_\lambda +\left(\mathbf a_\lambda^\dag\right)^2\right) | \alpha_\lambda \rangle \\ & = - \left[\mathscr E^{(1)}_\lambda\right]^2 \left(\alpha_\lambda^2 + \bar \alpha_\lambda ^2 - 2 |\alpha_\lambda|^2 - 1\right) \\ & = - \left[\mathscr E^{(1)}_\lambda\right]^2 \left[\left(\alpha_\lambda - \bar \alpha_\lambda\right)^2 - 1\right] \\ & = \left[\mathbf E_{\text{classical}}(\mathbf r,0) \right]^2 + \left[\mathscr E^{(1)}_\lambda\right]^2 \end{aligned}
The variance is therefore:
\begin{aligned} \left[\Delta \mathbf E(\mathbf r,0) \right]^2 & = \left[\langle \mathbf E \rangle (\mathbf r,0)\right]^2 - \left[\langle \mathbf E^2 \rangle (\mathbf r,0)\right]\\ & = \left[\mathbf E_{\text{classical}}(\mathbf r,0) \right]^2 + \left[\mathscr E^{(1)}_\lambda\right]^2 -\left[\mathbf E_{\text{classical}}(\mathbf r,0) \right]^2 \\ & = \left[\mathscr E^{(1)}_\lambda\right]^2 \end{aligned}
The calculation for a generic time t and position \mathbf r is similar, with the only change is complex exponential factors and their complex conjugates, whose product is one, so the final result is unchanged. The standard deviation is:
\Delta \mathbf E(\mathbf r,t) = \mathscr E^{(1)}_\lambda
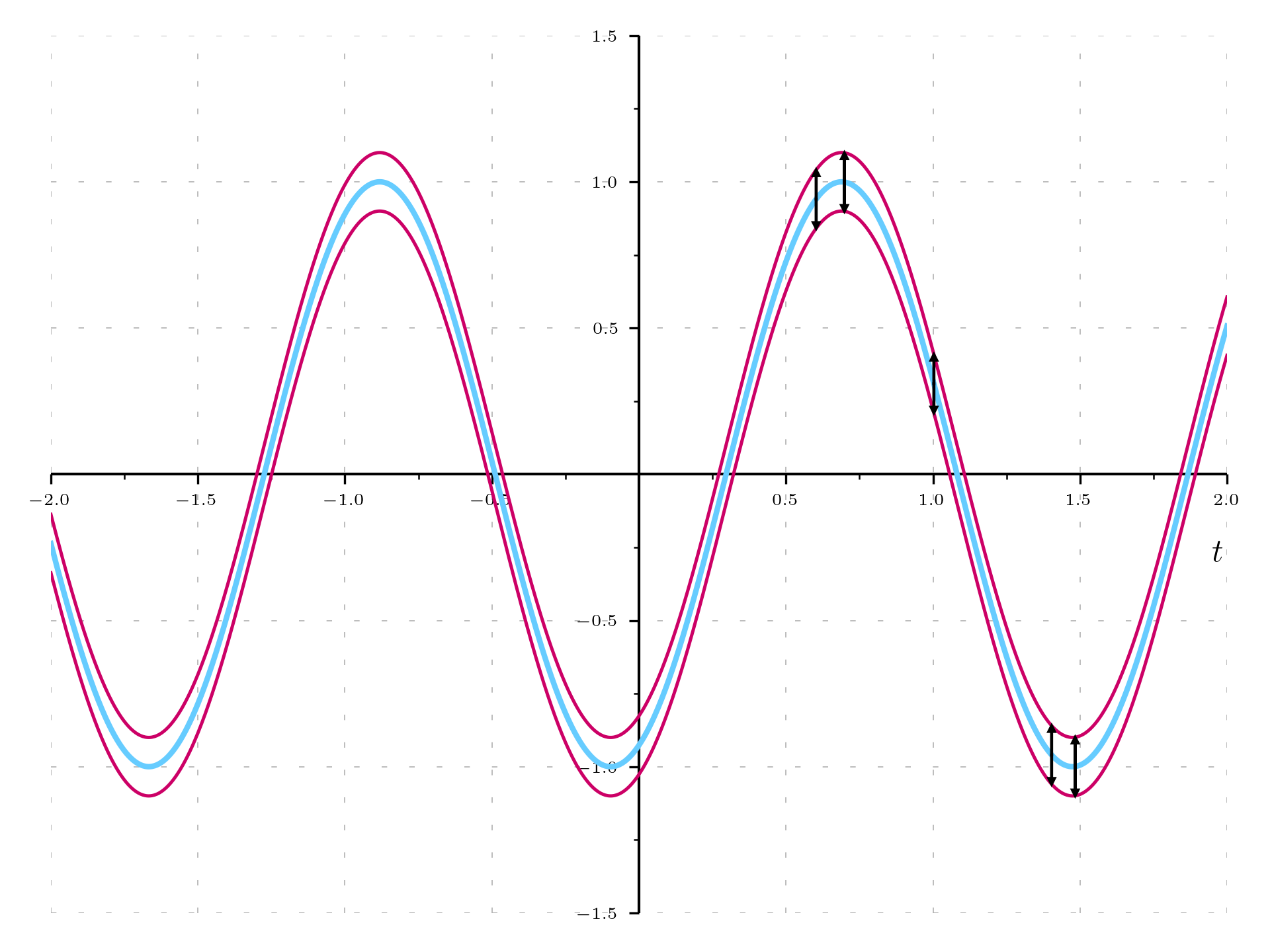
It is possible to plot the average and the standard deviation: making repeated measurements will gives the field in the area between the two red lines with high probability, and the blue line gives the ensemble average value of these measurements. The dispersion band has a constant height 2\mathscr E_\lambda, which can be verified by the arrows taken at some sample points.
As soon as the width of the band is small compared to the amplitude of the wave, the value is close to the average and the field behave like a classical field, it is almost a classical field and that is why it is called quasi-classical. The ratio of the dispersion to the amplitude is:
\frac{\text{dispersion}}{\text{amplitude}} = \frac{\Delta \mathbf E}{2\left| \alpha_\lambda \right| \mathscr E_\lambda} = \frac{\mathscr E_\lambda}{2\left| \alpha_\lambda \right| \mathscr E_\lambda} = \frac{1}{2\left| \alpha_\lambda \right|}
So the larger the value of \left| \alpha_\lambda \right|, the closer the state is to a classical state, corresponding to a situation where the number of photons in the quantization volume is large.
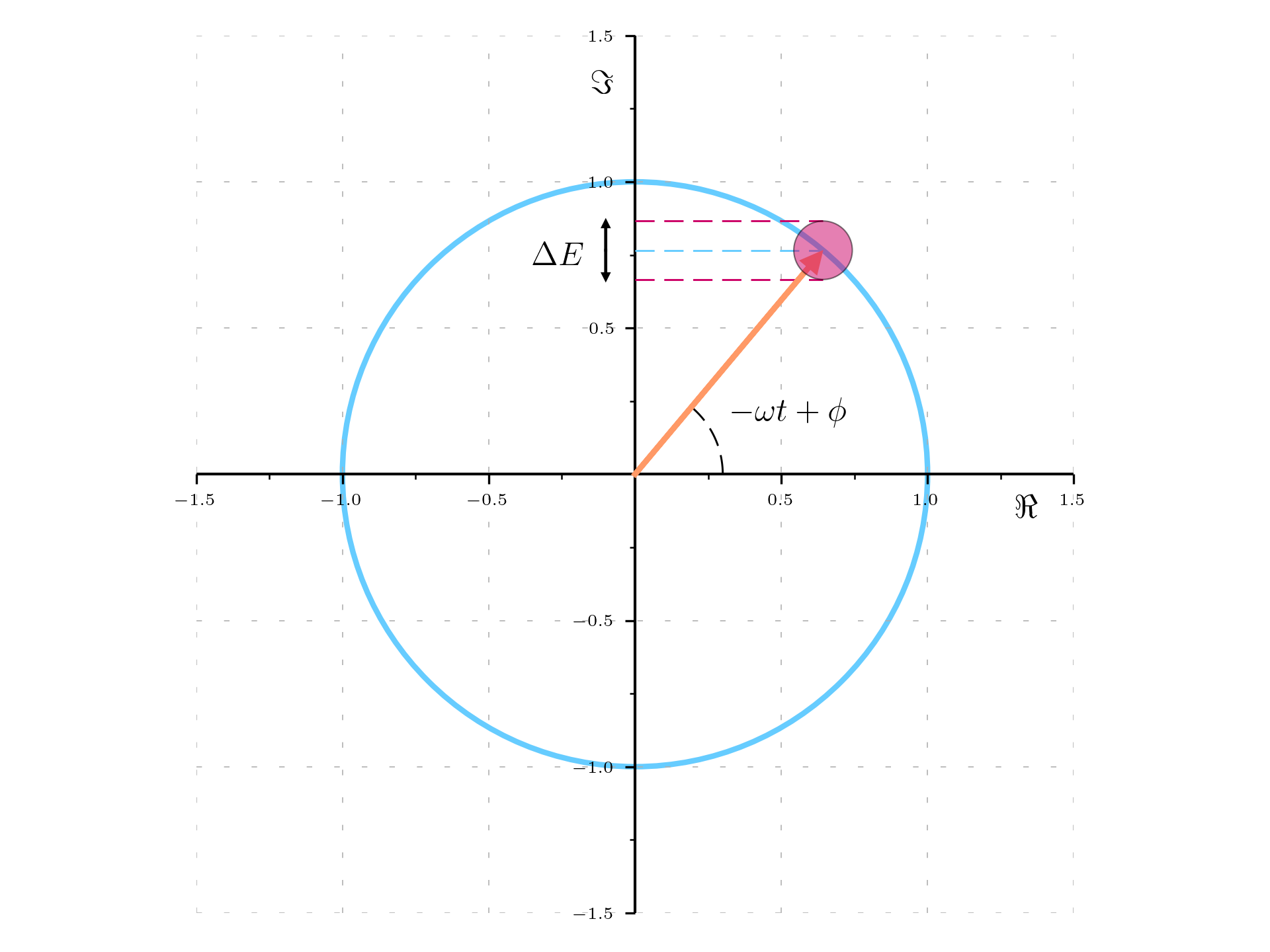
It is possible to represent the quasi classical state in the phasor plane which is a complex plane used to represent sinusoidal functions, like a classical electric field, as rotating vectors (phasors). The electric field \mathbf E(\mathbf r, t) =i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left(\mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda * t} - \mathbf a_\lambda^\dag e^{-i\mathbf{k}_\lambda \cdot \mathbf{r} + \omega_\lambda * t} \right) is represented by a phasor.
The electric field average is twice the projection of the phasor on the imaginary axis (\mathbf E(\mathbf r, t) =2*\mathbf{e}_\lambda \Im\left\{\mathscr E^{(1)}_\lambda \mathbf a_\lambda e^{i\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda * t}\right\}). This representation is useful to represent the dispersion of the measurement result using a disk of radius \Delta E centered on the phasor of the average field. The projection on each axis represents the dispersion of the field at each moment. This representation is useful when dealing with squeezed light state as the shape is no longer circular.
A similar computation can be done for the energy, from:
\mathbf H = \hbar \omega_\lambda\left(\mathbf a^\dag \mathbf a + \frac{1}{2}\right)
The expectation is:
\begin{aligned} \langle \alpha_\lambda| \mathbf H | \alpha_\lambda\rangle & = \langle \alpha_\lambda| \hbar \omega_\lambda\left(\mathbf a^\dag \mathbf a + \frac{1}{2}\right) | \alpha_\lambda\rangle = \hbar \omega_\lambda \left( \left(\langle \alpha_\lambda| \mathbf a^\dag\right)\left( \mathbf a | \alpha_\lambda\rangle\right) + \frac{1}{2} \langle \alpha_\lambda| \alpha_\lambda\rangle \right) \\ & = \hbar \omega_\lambda \left(\alpha_\lambda \bar\alpha_\lambda\langle \alpha_\lambda| \alpha_\lambda\rangle + \frac{1}{2} \right) = \hbar \omega_\lambda \left(|\alpha_\lambda|^2 + \frac{1}{2} \right) \end{aligned}
The probability P(n_\lambda) of finding the system in the state |n_\lambda\rangle when it is in the coherent state |\alpha_\lambda\rangle is given by the modulus squared of the coefficient of |n_\lambda\rangle in the expansion of |\alpha_\lambda\rangle.
The coefficient of |n_\lambda\rangle is:
c_{n_\lambda} = e^{-\frac{|\alpha_\lambda|^2}{2}} \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}}
The probability P(n_\lambda) is:
\begin{aligned} P(n_\lambda) & = |c_{n_\lambda}|^2 = \left| e^{-\frac{|\alpha_\lambda|^2}{2}} \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} \right|^2 \\ & = \left( e^{-\frac{|\alpha_\lambda|^2}{2}} \right)^2 \frac{\left(|\alpha_\lambda|^2\right)^{n_\lambda}}{n_\lambda!} = e^{-|\alpha_\lambda|^2} \frac{\left(|\alpha_\lambda|^2\right)^{n_\lambda}}{n_\lambda!} \end{aligned}
which is a Poisson distribution with average |\alpha_\lambda|^2 and variance |\alpha_\lambda|^2. That can be computed quantum mechanically. The average is the number operator:
\langle \mathbf N_\lambda \rangle = \langle \alpha_\lambda| \mathbf a^\dag \mathbf a | \alpha_\lambda\rangle = \left(\langle \alpha_\lambda| \mathbf a^\dag \right)\left(\mathbf a | \alpha_\lambda\rangle\right) = | \alpha_\lambda|^2 \langle \alpha_\lambda|\alpha_\lambda\rangle = |\alpha_\lambda|^2
That gives a simple representation of \alpha_\lambda as the number of photons in the quantization volume. Since it is not an eigenvalue of the number operator, there is a dispersion on the number of photons.
The variance is given by:
\begin{aligned} \left(\Delta \mathbf N_\lambda\right)^2 & = \langle \mathbf N_\lambda^2 \rangle - \langle \mathbf N_\lambda \rangle ^2 = \langle \alpha_\lambda| \mathbf a^\dag \mathbf a\mathbf a^\dag \mathbf a | \alpha_\lambda\rangle - |\alpha_\lambda|^4 \\ & = \langle \alpha_\lambda| \mathbf a^\dag \left(1 + \mathbf a^\dag \mathbf a \right) \mathbf a | \alpha_\lambda\rangle - |\alpha_\lambda|^4 \\ & = \langle \alpha_\lambda| \mathbf a^\dag \mathbf a | \alpha_\lambda\rangle + \langle \alpha_\lambda| \mathbf a^\dag \mathbf a^\dag \mathbf a \mathbf a | \alpha_\lambda\rangle - |\alpha_\lambda|^4 \\ & = |\alpha_\lambda|^2 + \left(\langle \alpha_\lambda| \mathbf a^\dag\right) \mathbf a^\dag \mathbf a \left(\langle \mathbf a | \alpha_\lambda\rangle\right) - |\alpha_\lambda|^4 \\ & = |\alpha_\lambda|^2 + |\alpha_\lambda|^2 \langle \alpha_\lambda | \mathbf a^\dag \mathbf a | \alpha_\lambda\rangle - |\alpha_\lambda|^4 \\ & = |\alpha_\lambda|^2 + |\alpha_\lambda|^4 - |\alpha_\lambda|^4 = |\alpha_\lambda|^2 \end{aligned}
So the dispersion of the number of photons is proportional to the square root of the number of photons:
\Delta \mathbf N_\lambda = |\alpha_\lambda| = \sqrt{\langle \mathbf N_\lambda \rangle}
From these two values it is possible to compute the average dispersion of the number of photons:
\frac{\Delta \mathbf N_\lambda}{\langle \mathbf N_\lambda \rangle} = \frac{1}{\sqrt{\langle \mathbf N_\lambda \rangle}} = \frac{1}{|\alpha_\lambda|} If \alpha_\lambda is large enough, then the dispersion becomes negligible.
Time evolution
Using a unitary time evolution operator \mathbf U the wave function is evolving as:
|\psi(t)\rangle = \sum_{n=0}^\infty c_n e^{-i \omega_\lambda \left(n + \frac{1}{2}\right)t} |\mathbf{n}\rangle
Using the coefficients for the coherent state:
\begin{aligned} |\psi(t)\rangle & = \sum_{n=0}^\infty e^{-\frac{|\alpha_\lambda|^2}{2}} \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} e^{-i \omega_\lambda \left(n + \frac{1}{2}\right)t} |\mathbf n_\lambda\rangle \\ & = e^{\frac{-i \omega_\lambda t}{2}} \sum_{n=0}^\infty e^{-\frac{|\alpha_\lambda|^2}{2}} \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} e^{-i \omega_\lambda n t} |\mathbf n_\lambda\rangle \\ & = e^{\frac{-i \omega_\lambda t}{2}} | \alpha_0 e^{-i\omega_\lambda } \rangle \end{aligned}
Quadrature fluctuations
There is a different way to consider the dispersion of the electric field measurements.
Considering the operators:
\begin{aligned} & \mathbf Q = \sqrt{\frac{\hbar}{2}}\left(\mathbf a + \mathbf a^\dag\right) \\ & \mathbf P = -i\sqrt{\frac{\hbar}{2}}\left(\mathbf a - \mathbf a^\dag\right) \end{aligned} The electric field can be expressed as function of these observables:
\mathbf E(\mathbf r) = \sqrt {\frac{2}{\hbar}}\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \left[\cos(\mathbf{k}_\lambda \cdot \mathbf{r}) \mathbf P_\lambda - \sin(\mathbf{k}_\lambda \cdot \mathbf{r}) \mathbf Q_\lambda \right]
Computing their fluctuations, starting from the average value:
\begin{aligned} \langle \mathbf Q \rangle & = \langle \psi(t) | \sqrt{\frac{\hbar}{2}}\left(\mathbf a + \mathbf a^\dag\right) | \psi(t) \rangle \\ & = \sqrt{\frac{\hbar}{2}} e^{\frac{i \omega_\lambda t}{2}} \langle \alpha_0 e^{i\omega_\lambda} | \left(\mathbf a + \mathbf a^\dag\right) | e^{\frac{-i \omega_\lambda t}{2}} | \alpha_0 e^{-i\omega_\lambda } \rangle \\ & = \sqrt{\frac{\hbar}{2}} \langle \alpha_0 | \left(\mathbf a + \mathbf a^\dag\right) | \alpha_0 \rangle = \sqrt{\frac{\hbar}{2}} \left(\alpha + \bar \alpha\right)\\ \langle \mathbf P \rangle & = \langle \psi(t) | -i\sqrt{\frac{\hbar}{2}}\left(\mathbf a - \mathbf a^\dag\right)| \psi(t) \rangle \\ & = -i\sqrt{\frac{\hbar}{2}} e^{\frac{i \omega_\lambda t}{2}} \langle \alpha_0 e^{i\omega_\lambda} | \left(\mathbf a - \mathbf a^\dag\right) | e^{\frac{-i \omega_\lambda t}{2}} | \alpha_0 e^{-i\omega_\lambda } \rangle \\ & = -i\sqrt{\frac{\hbar}{2}} \langle \alpha_0 | \left(\mathbf a - \mathbf a^\dag\right) | \alpha_0 \rangle = -i\sqrt{\frac{\hbar}{2}} \left(\alpha - \bar \alpha\right)\\ \end{aligned}
Then computing the average squared:
\begin{aligned} \langle \mathbf Q^2 \rangle & = \langle \psi(t) | \frac{\hbar}{2} \left(\mathbf a + \mathbf a^\dag\right)^2 | \psi(t) \rangle \\ & = \frac{\hbar}{2} e^{\frac{i \omega_\lambda t}{2}} \langle \alpha_0 e^{i\omega_\lambda} | \left(\mathbf a + \mathbf a^\dag\right)^2 | e^{\frac{-i \omega_\lambda t}{2}} | \alpha_0 e^{-i\omega_\lambda } \rangle \\ & = \frac{\hbar}{2} \langle \alpha_0 | \left(\mathbf a + \mathbf a^\dag\right)^2 | \alpha_0 \rangle = \frac{\hbar}{2} \langle \alpha_0 | \left(\mathbf a^2 + \mathbf a\mathbf a^\dag + \mathbf a^\dag\mathbf a +\left(\mathbf a^\dag\right)^2\right) | \alpha_0 \rangle \\ & = \frac{\hbar}{2} \langle \alpha_0 | \left(\mathbf a^2 + 1 + 2 \mathbf a^\dag\mathbf a +\left(\mathbf a^\dag\right)^2\right) | \alpha_0 \rangle = \frac{\hbar}{2} \left(\alpha^2 + \bar \alpha ^2 + 2 |\alpha|^2 + 1\right) \\ & = \frac{\hbar}{2} \left[\left(\alpha + \bar \alpha\right)^2 + 1\right] \\ \langle \mathbf P^2 \rangle & = \langle \psi(t) | -i^2\sqrt{\frac{\hbar}{2}}\left(\mathbf a - \mathbf a^\dag\right)^2| \psi(t) \rangle \\ & = -\frac{\hbar}{2} e^{\frac{i \omega_\lambda t}{2}} \langle \alpha_0 e^{i\omega_\lambda} | \left(\mathbf a - \mathbf a^\dag\right)^2 | e^{\frac{-i \omega_\lambda t}{2}} | \alpha_0 e^{-i\omega_\lambda } \rangle \\ & = -\frac{\hbar}{2} \langle \alpha_0 | \left(\mathbf a - \mathbf a^\dag\right)^2 | \alpha_0 \rangle = -\frac{\hbar}{2} \langle \alpha_0 | \left(\mathbf a^2 - \mathbf a\mathbf a^\dag - \mathbf a^\dag\mathbf a +\left(\mathbf a^\dag\right)^2\right) | \alpha_0 \rangle \\ & = -\frac{\hbar}{2} \langle \alpha_0 | \left(\mathbf a^2 - 1 - 2 \mathbf a^\dag\mathbf a +\left(\mathbf a^\dag\right)^2\right) | \alpha_0 \rangle = -\frac{\hbar}{2} \left(\alpha^2 + \bar \alpha ^2 - 2 |\alpha|^2 - 1\right) \\ & = -\frac{\hbar}{2} \left[\left(\alpha - \bar \alpha\right)^2 - 1\right] \end{aligned}
Finally the fluctuations:
\begin{aligned} \left(\Delta Q\right)^2 & = \langle \mathbf Q^2 \rangle - \langle \mathbf Q \rangle ^2 \\ & = \frac{\hbar}{2} \left[\left(\alpha + \bar \alpha\right)^2 + 1\right] - \left[\sqrt{\frac{\hbar}{2}} \left(\alpha + \bar \alpha\right)\right]^2 = \frac{\hbar}{2} \\ \left(\Delta P\right)^2 & = \langle \mathbf P^2 \rangle - \langle \mathbf P \rangle ^2 \\ & = -\frac{\hbar}{2} \left[\left(\alpha - \bar \alpha\right)^2 - 1\right] - \left[-i\sqrt{\frac{\hbar}{2}} \left(\alpha - \bar \alpha\right)\right]^2 = \frac{\hbar}{2} \end{aligned}
The Heisenberg Uncertainty Principle for Q and momentum P can be expressed as:
\sigma_Q \sigma_P \geq \frac{\hbar}{2}
For the coherent state the result is:
\Delta Q \Delta P = \sqrt{\left(\Delta Q\right)^2}\sqrt{\left(\Delta P\right)^2} = \frac{\hbar}{2}
It shows that coherent states are minimum uncertainty states, where the product of the uncertainties reaches the theoretical lower bound established by quantum mechanics; the value coincide with the amplitude of vacuum fluctuation. This is also called the standard quantum limit, which is the value of minimal quantum noise.
Photodetection rate
\mathbf{E}^{(+)}(\mathbf{r}, t) | \alpha_\lambda \rangle = i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \mathbf a_\lambda e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} | \alpha_\lambda \rangle
with an eigenvalue equal to the mean of the electric field:
i\mathbf{e}_\lambda \mathscr E^{(1)}_\lambda \mathbf a_\lambda e^{i(\mathbf{k}_\lambda \cdot \mathbf{r} - \omega_\lambda t)} = \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t)
With the Heisenberg representation it is straightforward to calculate the average of the electric field:
\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t) = \langle \alpha_\lambda(t) | \mathbf{E}^{(+)}(\mathbf{r}) | \alpha_\lambda(t) \rangle = \langle \alpha_\lambda | \mathbf{E}^{(+)}(\mathbf{r},t) | \alpha_\lambda \rangle
It is possible now to get the photo-electric signals. Starting from the single photo-detection signal:
\begin{aligned} w^{(1)}(\mathbf{r}, t) & = s \left\|\mathbf{E}^{(+)}(\mathbf{r}, t) | \psi(0) \rangle \right\|^2 \\ & = s \left\|\mathbf{E}^{(+)}(\mathbf{r}, t) | \alpha_\lambda(0) \rangle \right\|^2 \\ & = s \left\langle \alpha_\lambda(0) \left| \mathbf{E}^{(-)}(\mathbf{r}, t) \mathbf{E}^{(+)}(\mathbf{r}, t) \right| \alpha_\lambda(0) \right\rangle \\ & = s \left\langle \alpha_\lambda(0) \left| \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}, t) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t) \right| \alpha_\lambda(0) \right\rangle \\ & = s \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}, t) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t) \left\langle \alpha_\lambda(0) | \alpha_\lambda(0) \right\rangle \\ & = s \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t)\right|^2 \left\langle \alpha_\lambda(0) | \alpha_\lambda(0) \right\rangle \\ & = s \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}, t)\right|^2 \end{aligned}
This is the same results that than be calculated for a semi-classical field. A similar calculation can be done for the double detection:
\begin{aligned} w^{(2)}(\mathbf{r}_1, t_1, \mathbf{r}_2, t_2) & = s^2 \left\| \mathbf{E}^{(+)}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}(\mathbf{r}_1, t_1) | \psi(0) \rangle \right\|^2 \\ & = s^2 \left\| \mathbf{E}^{(+)}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}(\mathbf{r}_1, t_1) | \alpha_\lambda(0) \rangle \right\|^2 \\ & = s^2 \left\langle \alpha_\lambda(0) \left| \mathbf{E}^{(-)}(\mathbf{r}_1, t_1) \mathbf{E}^{(-)}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}(\mathbf{r}_1, t_1) \right| \alpha_\lambda(0) \right\rangle \\ & = s^2 \left\langle \alpha_\lambda(0) \left| \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}_1, t_1) \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_1, t_1) \right| \alpha_\lambda(0) \right\rangle \\ & = s^2 \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}_1, t_1) \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_1, t_1) \langle \alpha_\lambda(0) | \alpha_\lambda(0) \rangle \\ & = s^2 \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}_1, t_1) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_1, t_1) \mathbf{E}^{(-)}_{\text{classical}}(\mathbf{r}_2, t_2) \mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_2, t_2) \\ & = s^2 \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_1, t_1) \right|^2 \left|\mathbf{E}^{(+)}_{\text{classical}}(\mathbf{r}_2, t_2) \right|^2 \\ & = w^{(1)}(\mathbf{r}_1, t_1) w^{(1)}(\mathbf{r}_2, t_2) \end{aligned}
This result is in contrast which what we had found for the case of a single photon, for which the double detection is null even if both single detection are different from zero. The two should not be confused because the above relationship is true even for weak quasi-classical states with alpha smaller than one, so that the average number of photons is less than one.
Beam splitter
Let’s consider a beam splitter, in which there are two input modes (1) and (2) and two output modes (3) and (4), with a unitary transformation \mathbf U which link the state | \Psi_{12} \rangle with |\Psi_{34} \rangle.
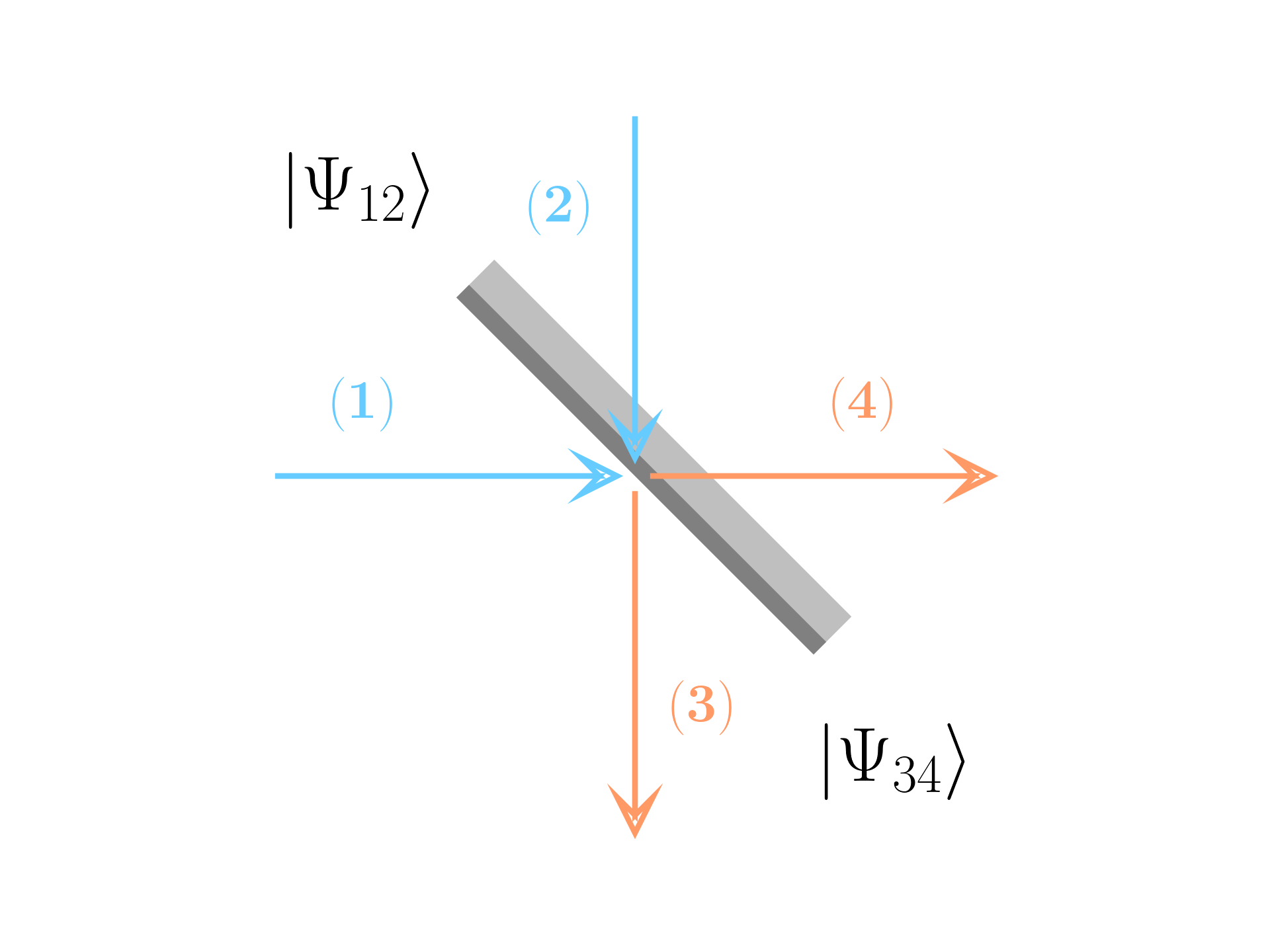
This can be seen as a transformation that link the states on the two sides of the splitter; if all the states are considered, then the matrix dimension became quickly very large because it is necessary to consider a combination of all the states \mathbf U (n_1, n_2, \dots). A solution to this problem is to transform the electric field in place of the states (as explained in details here, and this involve only a 2 \times 2 symmetric matrix:
\begin{bmatrix} \mathbf E_3^{(+)} \\ \mathbf E_4^{(+)} \end{bmatrix} = \begin{bmatrix} r & t \\ t & -r \end{bmatrix} \begin{bmatrix} \mathbf E_1^{(+)} \\ \mathbf E_2^{(+)} \end{bmatrix}
This matrix is the same as the one for the classical field (considering in the specific case coefficient which are real so that calculation at a later stage will be slightly simpler) and the coefficients obey to:
r^2 + t^2 = 1
This relation is also valid for the destruction operators:
\begin{bmatrix} \mathbf a_3 \\ \mathbf a_4\end{bmatrix} = \begin{bmatrix} r & t \\ t & -r \end{bmatrix} \begin{bmatrix} \mathbf a_1 \\ \mathbf a_2 \end{bmatrix}
Using the commutator relation in the input space:
[\mathbf{a}_1, \mathbf{a}_1] = 1, \quad [\mathbf{a}_2, \mathbf{a}_2] = 1, \quad [\mathbf{a}_1, \mathbf{a}_2] = 0
These formulas were also demonstrated for the output space:
[\mathbf{a}_3, \mathbf{a}_3] = 1, \quad [\mathbf{a}_4, \mathbf{a}_4] = 1, \quad [\mathbf{a}_3, \mathbf{a}_4] = 0 Output quantities can be expressed as function of the input states; for example the single detection probability at (4) can be expressed as:
\begin{aligned} w^{(1)}(\mathbf r_4,t) & = s \left\| \mathbf E_4^{(+)} | \Psi_{34} \rangle \right\|^2 \\ & = s \left\| t\,\mathbf E_1^{(+)} - r\,\mathbf E_2^{(+)} | \Psi_{12} \rangle \right\|^2 \\ & = s \left[ \mathscr E^{(1)}_\lambda\right]^2 \left\|\left( t\,\mathbf a_1 - r\,\mathbf a_2 \right) | \Psi_{12} \rangle \right\|^2 \end{aligned}
For a semi-classical state \alpha with the vacuum in state (2), |\Psi_{12} \rangle = | \alpha \rangle_1 | \mathbf 0 \rangle:
w^{(1)}(\mathbf r_4,t) = s t^2 \left[ \mathscr E^{(1)}_\lambda\right]^2 | \alpha |^2
This calculation is generic and can be applied for example to the electric field observable:
| \Psi_{12} \rangle = | \alpha_1 e^{-i\omega t}\rangle | \mathbf 0 \rangle
Using the expression of the field as function of \mathbf a and \mathbf a^\dag, it is possible to express \mathbf E_3(\mathbf r) as:
\begin{aligned} \mathbf E_3(\mathbf r) & = i\mathbf{e}_3 \mathscr E^{(1)}_\omega \left(\mathbf a_1 e^{i\mathbf{k}_3 \cdot \mathbf{r}} + \mathbf a_1^\dag e^{-i\mathbf{k}_3 \cdot \mathbf{r}} \right) \\ & = i\mathbf{e}_3 \mathscr E^{(1)}_\omega \left(r \mathbf a_1 e^{i\mathbf{k}_3 \cdot \mathbf{r}} -r \mathbf a_1^\dag e^{-i\mathbf{k}_3 \cdot \mathbf{r}} \right) \end{aligned}
The contribution of (2) is null since we consider the vacuum in this channel.
The average of the field is:
\begin{aligned} \langle \Psi_{12} (t) | \mathbf E_3(\mathbf r) | \Psi_{12} (t) \rangle & =\langle \alpha_1 \langle \mathbf 0| e^{-i\omega t}| i\mathbf{e}_3 \mathscr E^{(1)}_\omega \left(r \mathbf a_1 e^{i\mathbf{k}_3 \cdot \mathbf{r}} -r \mathbf a_1^\dag e^{-i\mathbf{k}_3 \cdot \mathbf{r}} \right)| \alpha_1 e^{-i\omega t}\rangle | \mathbf 0 \rangle \\ & = i\mathbf{e}_1 \mathscr E^{(1)}_\omega \langle \alpha_1 \langle \mathbf 0| \left(r \mathbf a_1 e^{i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} -r \mathbf a_1^\dag e^{-i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} \right)| \alpha_1 \rangle | \mathbf 0 \rangle \\ & = i\mathbf{e}_1 \mathscr E^{(1)}_\omega \left(r \alpha_1 e^{i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} -r \bar \alpha_1 e^{-i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} \right) \end{aligned}
which is a quasi classical state r \alpha_1.
A similar calculation can be done for \mathbf E_4(\mathbf r):
\begin{aligned} \mathbf E_4(\mathbf r) & = i\mathbf{e}_4 \mathscr E^{(1)}_\omega \left(\mathbf a_1 e^{i\mathbf{k}_3 \cdot \mathbf{r}} + \mathbf a_1^\dag e^{-i\mathbf{k}_4 \cdot \mathbf{r}} \right) \\ & = i\mathbf{e}_4 \mathscr E^{(1)}_\omega \left(t \mathbf a_1 e^{i\mathbf{k}_4 \cdot \mathbf{r}} -t \mathbf a_1^\dag e^{-i\mathbf{k}_4 \cdot \mathbf{r}} \right) \end{aligned}
The average of the field is:
\begin{aligned} \langle \Psi_{12} (t) | \mathbf E_4(\mathbf r) | \Psi_{12} (t) \rangle & =\langle \alpha_1 \langle \mathbf 0| e^{-i\omega t}| i\mathbf{e}_4 \mathscr E^{(1)}_\omega \left(t \mathbf a_1 e^{i\mathbf{k}_4 \cdot \mathbf{r}} -t \mathbf a_1^\dag e^{-i\mathbf{k}_4 \cdot \mathbf{r}} \right)| \alpha_1 e^{-i\omega t}\rangle | \mathbf 0 \rangle \\ & = i\mathbf{e}_1 \mathscr E^{(1)}_\omega \langle \alpha_1 \langle \mathbf 0| \left(t \mathbf a_1 e^{i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} -t \mathbf a_1^\dag e^{-i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} \right) | \alpha_1 \rangle | \mathbf 0 \rangle \\ & = i\mathbf{e}_1 \mathscr E^{(1)}_\omega \left(t \alpha_1 e^{i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} -t \bar \alpha_1 e^{-i(\mathbf{k}_1 \cdot \mathbf{r} - \omega t)} \right) \end{aligned}
which is a quasi classical state t \alpha_1.
Therefore, these average values are transformed as the classical field would transform.
It is possible to express the state in the output space using the action of the creation operation \mathbf a^\dag on the vacuum; for example to represent a single photon in the input channel (1) can be represented as:
| \Psi_{12} \rangle = | \mathbf 1_1 \rangle |\mathbf 0_2 \rangle = \mathbf a_1^\dag |\mathbf 0 \rangle
Starting from the relationship of the destructor operators:
\begin{bmatrix} \mathbf a_3 \\ \mathbf a_4\end{bmatrix} = \begin{bmatrix} r & t \\ t & -r \end{bmatrix} \begin{bmatrix} \mathbf a_1 \\ \mathbf a_2 \end{bmatrix}
Inverting it (\det \mathbf S = -1):
\begin{bmatrix} \mathbf a_1 \\ \mathbf a_2\end{bmatrix} = \begin{bmatrix} r & t \\ t & -r \end{bmatrix} \begin{bmatrix} \mathbf a_3 \\ \mathbf a_4 \end{bmatrix}
And taking the Hermitian conjugate (t and r are real by construction):
\begin{bmatrix} \mathbf a_1^\dag \\ \mathbf a_2^\dag \end{bmatrix} = \begin{bmatrix} r & t \\ t & -r \end{bmatrix} \begin{bmatrix} \mathbf a_3^\dag \\ \mathbf a_4^\dag \end{bmatrix}
We can use these relations to express the state in the output space; for example in the previous case of one photon in input (1) and not photons in input (2) it gives:
| \Psi_{12} \rangle = | \mathbf 1_1 \rangle |\mathbf 0_2 \rangle = \mathbf a_1^\dag |\mathbf 0 \rangle = \left( r \mathbf a_3^\dag + t\mathbf a_4^\dag\right) |\mathbf 0 \rangle = r| \mathbf 1_3 \rangle |\mathbf 0_4 \rangle + t| \mathbf 0_3 \rangle |\mathbf 1_4 \rangle = | \Psi_{34} \rangle = | \Psi \rangle
The state is the same state | \Psi \rangle which can be expressed in either of the basis. This expression if there are many photons can became quite complicated if there are many photons in the input state, but for the quasi-classical states it takes a simple expression.
It is possible to do the same for semi-classical states, first expressing the decomposition as function of the creation operator:
| \alpha_\lambda \rangle = e^{-\frac{|\alpha_\lambda|^2}{2}} \sum_{n_\lambda = 0}^\infty \frac{\alpha_\lambda^{n_\lambda}}{\sqrt{n_\lambda!}} | \mathbf n_\lambda \rangle = e^{-\frac{|\alpha_\lambda|^2}{2}} \sum_{n_\lambda = 0}^\infty \frac{\left(\alpha_\lambda \mathbf a_\lambda^\dag\right)^{n_\lambda}}{n_\lambda!} | \mathbf 0 \rangle = e^{-\frac{|\alpha_\lambda|^2}{2}} e^{\alpha_\lambda \mathbf a_\lambda^\dag} | \mathbf 0 \rangle where the operator exponential has been used to simplify the expression:
e^{\alpha_\lambda \mathbf a_\lambda^\dag} \equiv \sum_{n_\lambda = 0}^\infty \frac{\left(\alpha_\lambda \mathbf a_\lambda^\dag\right)^{n_\lambda}}{n_\lambda!}
Using now \mathbf a_1^\dag = r \mathbf a_3^\dag + t\mathbf a_4^\dag previously calculated and substituting the expression for |\alpha_i \rangle:
\begin{aligned} | \Psi \rangle & = | \alpha \rangle_1 = e^{-\frac{|\alpha|^2}{2}} e^{\alpha \mathbf a_1^\dag} | \mathbf 0 \rangle = e^{-\frac{|\alpha|^2}{2}} e^{\alpha \left( r \mathbf a_3^\dag + t\mathbf a_4^\dag\right)} | \mathbf 0 \rangle \\ & = \left(e^{- (r^2+ t^2)\frac{|\alpha|^2}{2}} e^{\alpha r \mathbf a_3^\dag}e^{\alpha t\mathbf a_4^\dag} \right)| \mathbf 0 \rangle = \left[\left(e^{-r^2\frac{|\alpha|^2}{2}} e^{\alpha r \mathbf a_3^\dag}\right) \left(e^{-t^2\frac{|\alpha|^2}{2}} e^{\alpha t\mathbf a_4^\dag}\right) \right]| \mathbf 0 \rangle \\ & = | r \alpha \rangle_3 | t \alpha \rangle_4 \end{aligned}
So a quasi-classical state in the input channel generates two semi-classical states in each of the output channels with amplitude same as they would be for a classical field.