Exercise list
Lecture 1
Lecture 3
Lecture 1
Exercise 1.1
Show that the x coordinate of point Q in Fig. 1.6 is \sqrt{1-v^2}.
Considering a meterstick in the moving reference frame, which is represented by the segment of the line \overline{OR}; the point S sits at the intersection of two lines, x'=1 and t=0. In this case it is necessary to use the Lorentz transformation for the moving frame:
\begin{aligned} t & = \frac{t' + \frac{vx'}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}} \\ x & = \frac{x' + vt'}{\sqrt{1-\frac{v^2}{c^2}}} \end{aligned}
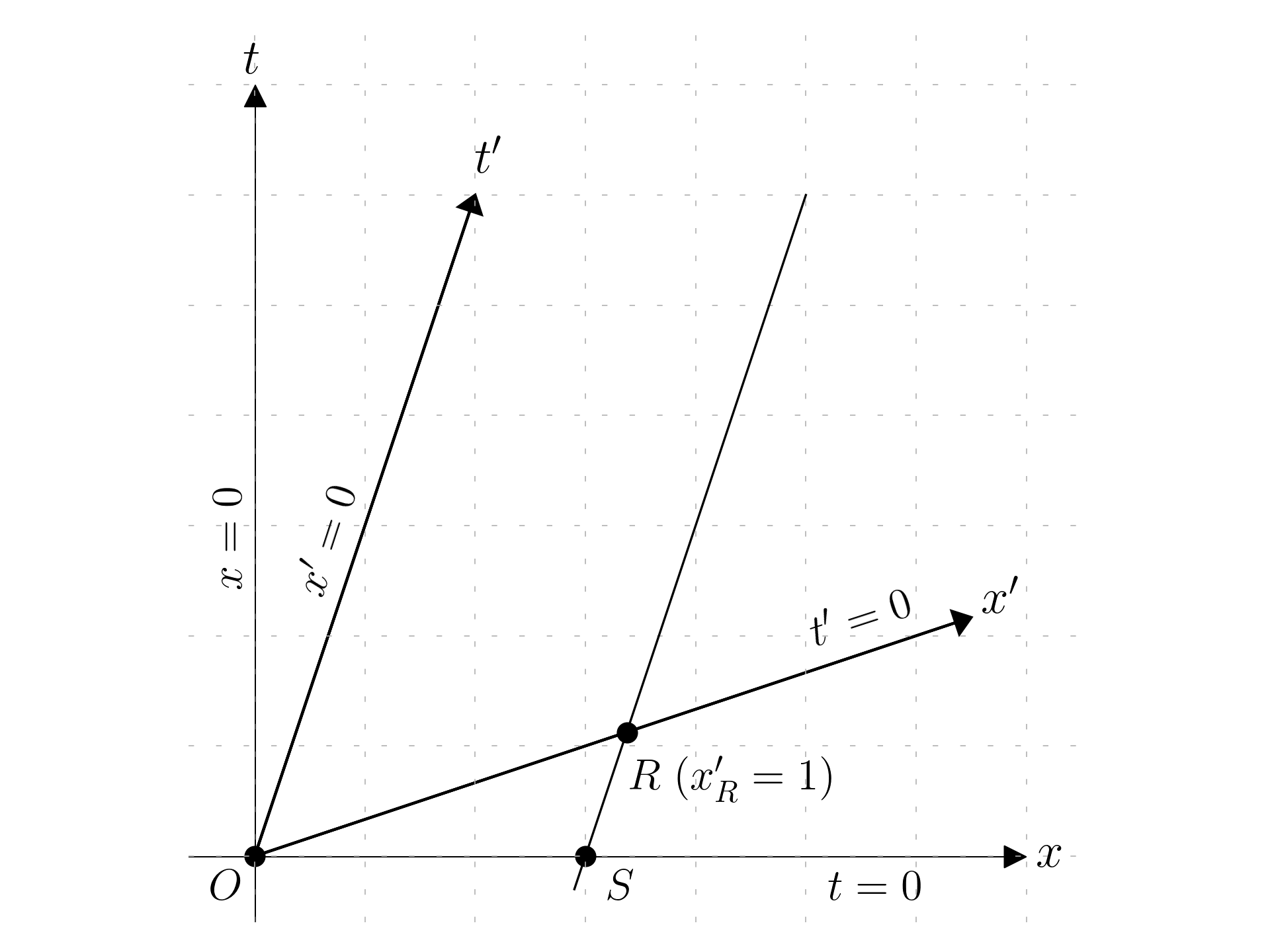
t=0 means:
t = \frac{t' + \frac{vx'}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}} = 0 \quad \Rightarrow \quad t' = -\frac{vx'}{c^2} Substituting this value in the second equation:
x = \frac{x' + vt'}{\sqrt{1-\frac{v^2}{c^2}}} = \frac{x' - \frac{v^2x'}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}} = \frac{x'\left(1 - \frac{v^2}{c^2}\right)}{\sqrt{1-\frac{v^2}{c^2}}} = x' \sqrt{1-\frac{v^2}{c^2}}
Since for the point R there is the condition x' = 1:
x = \sqrt{1-\frac{v^2}{c^2}}
Or, in relativistic units:
x = \sqrt{1-v^2}
Exercise 1.2
In Fig. 1.8, the traveling twin not only reverses direction but switches to a different reference frame when the reversal happens.
- Use the Lorentz transformation to show that before the reversal happens, the relationship between the twins is symmetrical. Each twin sees the other as aging more slowly than himself.
- Use spacetime diagrams to show how the traveler’s abrupt switch from one frame to another changes his definition of simultaneity. In the traveler’s new frame, his twin is suddenly much older than he was in the traveler’s original frame.
The exercise has been analyzed in details in a specific page here.
Lecture 3
Exercise 3.1
From the definition of (\Delta\tau)^2, verify Eq. 3.7.
Only 3 of the four component are independent; taking the definition of proper time:
(\mathrm d \tau)^2 = \left(\mathrm d X^0\right)^2 - \left[ \left(\mathrm d X^0\right)^2 + \left(\mathrm d X^1\right)^2 + \left(\mathrm d X^3\right)^2 \right]
and dividing by (\mathrm d\tau)^2:
\begin{aligned} &\left(\frac{\mathrm d \tau}{\mathrm d\tau}\right)^2 = \left(\frac{\mathrm d X^0}{\mathrm d\tau}\right)^2 - \left[ \left(\frac{\mathrm d X^0}{\mathrm d\tau}\right)^2 + \left(\frac{\mathrm d X^1}{\mathrm d\tau}\right)^2 + \left(\frac{\mathrm d X^3}{\mathrm d\tau}\right)^2 \right] \\ & 1 = \left (U^0 \right)^2 - \left[ \left (U^1 \right)^2 + \left (U^2 \right)^2 + \left (U^3 \right)^2 \right] \end{aligned}