Twin Paradox
The Twin Paradox in special relativity describes a scenario where one twin travels at near-light speed on a round trip, while the other remains on Earth. Upon the traveler’s return, they are younger than the Earth-bound twin—a result purely of time dilation effects under constant velocity as described by special relativity. The differential aging is a direct consequence of the distinct paths through spacetime taken by the twins, emphasizing the non-intuitive nature of time under high-speed travel conditions.
Time dilation is the origin of the so-called twin paradox; which involves two twins; let’s suppose that there are two identical twins, and one of the two is taking a high-speed journey and then returning back to the Earth; without loss of generality, it is possible to scale in a way that the inversion point is at t'=1. All the calculation will be done in relativistic units (so v = 1 means moving at the speed of light)
Before the inversion at the point P the situation is perfectly symmetrical; the watch of the moving observer move slower than the one of the fix observer as:
lets suppose to have a clock moving with an uniform velocity and to be stationary on the location x'=0 in the moving frame.
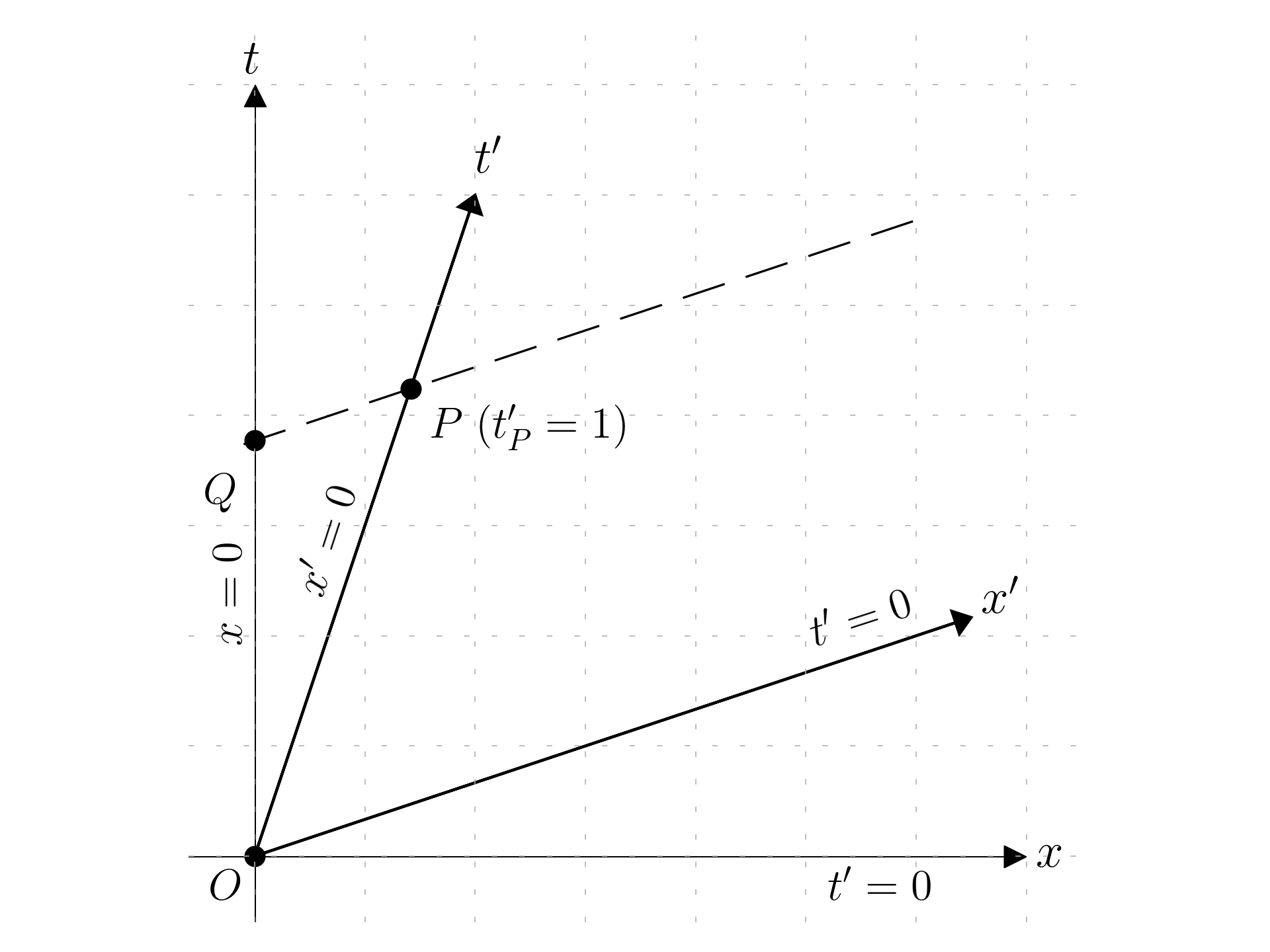
The watch moves on the t' axis which is represented by the equation x'=0, considering the instant in the moving frame t'=1, then considering the Lorentz transformation:
t = \frac{t' + vx'}{\sqrt{1-v^2}}
Plugging x' = 0 and t = 1 gives:
t = \frac{1}{\sqrt{1-v^2}}
Because the denominator is smaller than 1 then t > t'; and therefore moving clocks run slower by a factor \sqrt{1-v^2}:
t_{t'=0} = \frac{1}{\sqrt{1-v^2}} > 1
In the same way, considering now the point at t=1, x=0 in the fix observer reference frame, then a moving observer will see this point in spacetime as:
t' = \frac{t - vx}{\sqrt{1-v^2}} \bigg|_{t=1,x=0} = \frac{1}{\sqrt{1-v^2}}
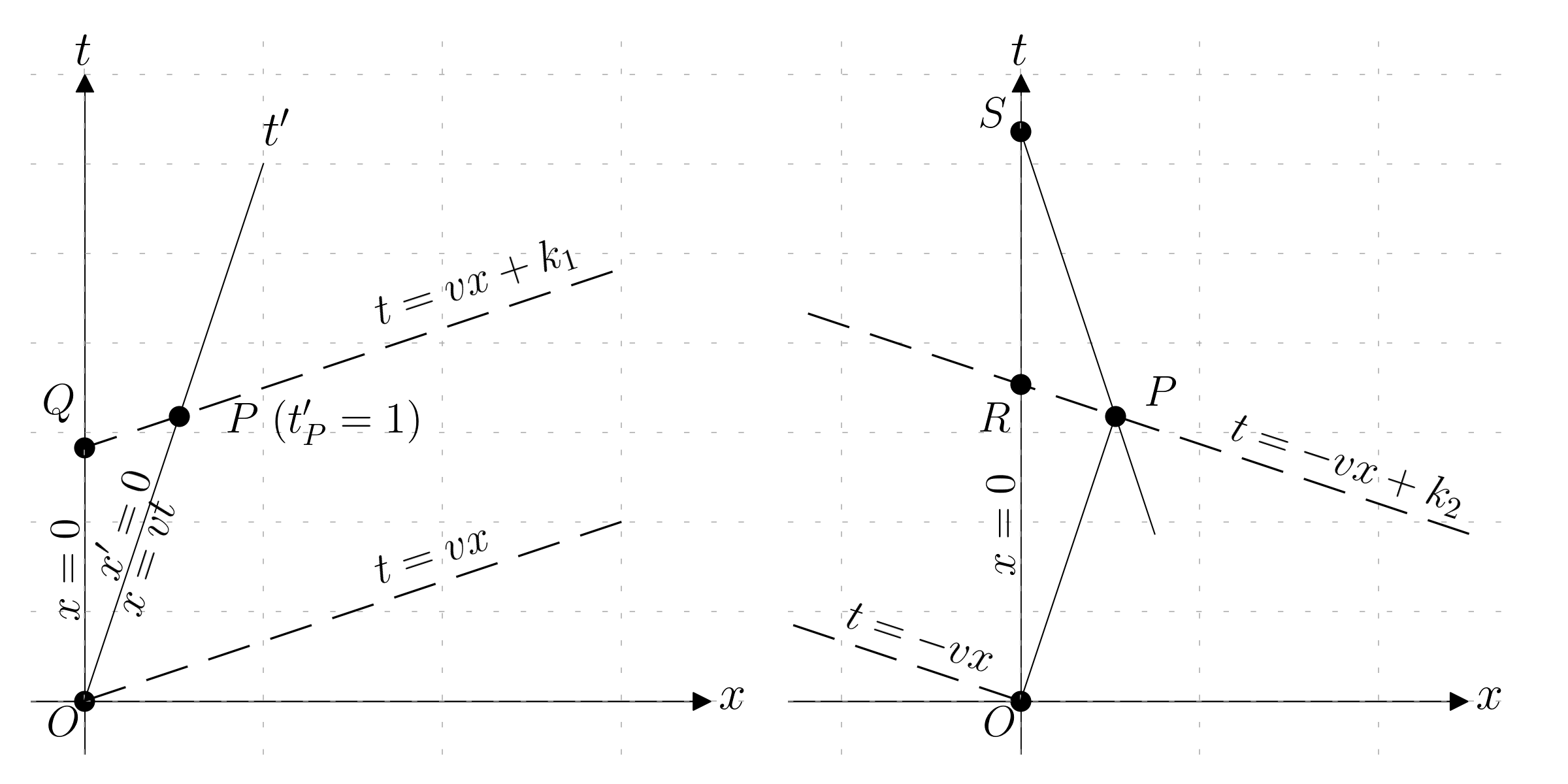
However, when the switch is performed at t' = 1 and the moving twin change the reference frame, then the definition of simultaneity for the twin who is changing the reference frame suddenly change.
Let’s consider first the first moving reference frame; the curve of simultaneity lies on parallel of the curve t=vx + k_1, where the constant k_1 depends from any point considered and for example, considering the point P, in the fix reference frame its coordinates are:
\begin{aligned} x_P & = \frac{x'+vt'}{\sqrt{1-v^2}} =\frac{v}{\sqrt{1-v^2}} \\ t_P & = \frac{t'+vx'}{\sqrt{1-v^2}} = \frac{1}{\sqrt{1-v^2}} \end{aligned}
Lets’ suppose that the reference frame has v_{rf}=0.8c, that gives (as coordinates based on c are already used), \sqrt{1-v^2}=\sqrt{1-0.8^2}=0.6:
\begin{aligned} x_P & = \frac{0.8}{0.6} \approx 1.33 \\ t_P & = \frac{1}{0.6} \approx 1.66 \end{aligned}
When t'=1 is passed before the observer change reference frame, he considers the time that lies on the current curve on simultaneity on the fix reference frame (point Q), that can be done first computing the constant k_1 (as one point of this line, P, is known):
k_1 = t_P - vx_P = \frac{1}{\sqrt{1-v^2}} - \frac{v^2}{\sqrt{1-v^2}} = \frac{1-v^2}{\sqrt{1-v^2}} = \sqrt{1-v^2}
as x_Q = 0:
t_Q = k_1 = \sqrt{1-v^2}
As expected, the moving observer assume that less time as been passed on the fix reference frame; for the example used:
t_Q = \sqrt{1 - v^2} = 0.6
Now the observer change reference frame and (instantaneously) jump to a reference frame moving with a velocity -v in the opposite direction, and at this point it is no longer true that the point simultaneous to the point P is Q but now the simultaneity curve is described by curves of the type t = -vx + k_2 and land on the point R; in this case too the constant k_2 can be computed:
k_2 = t_P + vx_P = \frac{1}{\sqrt{1-v^2}} + \frac{v^2}{\sqrt{1-v^2}} = \frac{1+v^2}{\sqrt{1-v^2}}
as x_R = 0:
t_R =-vx_R + k_2 = k_2 = \frac{1+v^2}{\sqrt{1-v^2}}
Now the time passed on the reference frame has an instantaneous jump:
t_R = \frac{1+v^2}{\sqrt{1-v^2}} = \frac{1+0.64}{0.6} \approx 2.73
The jump is equal to:
\Delta T_{RQ} = t_R - t_Q = \frac{1+v^2}{\sqrt{1-v^2}} - \frac{1-v^2}{\sqrt{1-v^2}} = \frac{2v^2}{\sqrt{1-v^2}}
In the particular example:
\Delta T_{RQ} = \frac{2 \times 0.64}{0.6} \approx 2.13
The point S lie on the curve x=-vt+k_3, than can be computed with the coordinates of the point P:
k_3 = x_P + vt_P = \frac{v}{\sqrt{1-v^2}} + \frac{v}{\sqrt{1-v^2}} = \frac{2v}{\sqrt{1-v^2}}
which gives the final point:
t_S = -\frac{x_S + k_3}{v} = \frac{k_3}{v} = \frac{2}{\sqrt{1-v^2}}
For the example considered:
T_S = \frac{2}{\sqrt{1-v^2}} = \frac{2}{0.6} \approx 3.33
For the return leg of the traveling twin, the point P has the time coordinates:
t''_P = \frac{t_P + vx_P}{\sqrt{1-v^2}} = \frac{1+v^2}{1-v^2}
The point S has the time coordinates:
t''_S = \frac{t_S + vx_S}{\sqrt{1-v^2}} = \frac{2}{1-v^2}
And the elapsed time in the second moving frame is:
\Delta T''_{SP} = t''_S - t''_p = \frac{2}{1-v^2} - \frac{1+v^2}{1-v^2} = \frac{2 -1 -v^2}{1-v^2} = \frac{1 - v^2}{1-v^2} = 1
So, also the return leg has length 1 (that could have been done purely with symmetry considerations), and while for the traveler twin 2 years passed, for the one stay in the frame at rest passed 3.33 years.
There are no contradictions because one transfers from the outgoing inertial frame to the incoming inertial frame there is a jump discontinuity in the age of the Earth-based twin, as demonstrated considering the different curve of simultaneity. Another point of confusion might arise from simple geometry, because considering the diagram and the segment \overline{OPS}, this segment is shorted than the segment \overline{OS}, so considering the triangle, the sum of two sides are shorter than the length of the third side, which contradict the geometric message that could be get from the graph.