Double Slit Experiment For Electrons
Simulation of 2D Schrödinger Equation
Accumulation of Probability Density
Introduction
The double-slit experiment, first conducted by Thomas Young in 1801, demonstrated the wave nature of light. In this setup, light passes through two slits and creates an interference pattern on a screen, indicative of wave behavior. The alternating light and dark fringes are a result of constructive and destructive interference between the light waves from each slit.
When applied to particles such as electrons, this experiment plays a key role in illustrating wave-particle duality. If electrons are fired one at a time through the slits, an interference pattern still emerges over time, despite each electron being a discrete particle. This suggests that electrons exhibit both particle-like and wave-like properties.
In quantum mechanics, this wave-like behavior is described by the electron’s wavefunction, which follows the principles of Schrödinger’s equation. The probability distribution of detecting the electron at various points on the screen forms the interference pattern.
This experiment fundamentally challenges classical intuition, showing that matter at a quantum scale does not adhere to traditional particle-only behavior. The experiment is essential in understanding quantum superposition and the role of measurement in collapsing a quantum system’s wavefunction.
If light or matter behaved purely as particles, then when fired in a straight line through a slit and allowed to strike a screen on the other side, we would expect to see a pattern on the screen that mirrors the size and shape of the slit. Each particle would travel through the slit, maintaining its trajectory, and create a single bright region directly opposite the slit, without any spreading or interference.
In the case of two slits, for purely particle-like behavior, we would expect to see two distinct bright regions on the screen, corresponding to the positions of each slit. There would be no interaction or overlap between the particles passing through each slit, and no interference pattern would emerge.
When the “single-slit experiment” is performed, the pattern observed on the screen is not a simple particle-like image, but rather a diffraction pattern, where the light spreads out after passing through the slit. This spread increases as the slit narrows, demonstrating the wave nature of light. The central bright band is the most intense, surrounded by fainter side bands, indicating regions where the light waves constructively and destructively interfere.
The top portion of the image in typical experiments shows this diffraction pattern, where a red laser illuminating the slit produces a bright central band, with two faint side bands on either side. With more refined equipment, more of these side bands can be observed, each corresponding to areas where the light waves either reinforce or cancel each other out. This phenomenon is explained by diffraction, where the slit acts as a source of new wavefronts, leading to interference of the light waves emanating from different points along the slit.
The later discovery of the photoelectric effect revealed that, under certain conditions, light behaves as if it is composed of discrete particles, or photons. In this phenomenon, light striking a metal surface ejects electrons, and the energy of these ejected electrons depends on the frequency of the light, not its intensity. This particle-like behavior could not be explained by classical wave theory.
These seemingly contradictory behaviors—wave-like diffraction and particle-like emission in the photoelectric effect—led to the development of quantum theory. This framework reconciles these observations by introducing the concept of wave-particle duality, where light (and matter) exhibits both wave and particle properties depending on the context of the experiment.
Free electron
A wavepacket for a free electron can be represented by a superposition of plane waves. The general form of the wavepacket is:
\Psi(x,t) = \int_{-\infty}^{\infty} A(k) e^{i(kx - \omega t)} \, \mathrm dk
where:
- A(k) is the amplitude as a function of wavenumber k,
- \omega is the angular frequency related to k through the dispersion relation \omega(k) = \frac{\hbar k^2}{2m} for a free particle,
- \Psi(x,t) is the wavefunction of the electron.
In practice, the wavepacket is often approximated using a Gaussian distribution in k-space for a localized wavepacket:
\Psi(x,t) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{-\frac{(k-k_0)^2}{2\sigma_k^2}} e^{i(kx - \omega t)} \, \mathrm dk
where:
- k_0 is the central wavenumber.
- \sigma_k is the spread in wavenumber, which relates to the localization of the wavepacket.
The de Broglie relation connects a particle’s momentum p to its wavelength \lambda:
\lambda = \frac{h}{p}
where:
- \lambda is the de Broglie wavelength.
- h is Planck’s constant.
- p = mv is the momentum of the particle, where m is the mass and v is the velocity.
As the momentum p increases, the wavelength \lambda decreases. This means the spacing between the fringes in the interference pattern also decreases, leading to a finer interference pattern.
In terms of wavepackets, increasing the momentum k_0 narrows the spatial spread of the wavepacket, while increasing \sigma_k results in a more localized packet. A higher momentum also leads to faster oscillations of the wavepacket fringes, representing higher energy.
Simulation setup
In this article, I will describe the simulation of the electron double-slit experiment in three main parts:
-
Simulation of 2D Schrödinger Equation: A wavepacket is propagated through the double slit using the time-dependent 2D Schrödinger equation. This simulates the quantum wave dynamics of the electron.
-
Accumulation of Probability Density: The probability density of the wavepacket is recorded on a screen placed after the double slit, tracking the likelihood of electron detection at various points.
-
Electron Beam Simulation: Based on the accumulated probability density, simulate the impact pattern of thousands of electrons on the screen to visualize the interference pattern typical of an electron beam experiment.
Simulation of 2D Schrödinger equation
The simulation of a 2D Schrodinger equation is described in details here. The only addition has been to add the possibility to draw an arbitrary number of slits in the middle barrier.
def V(self, x, y):
V_real = np.zeros_like(x)
if p.middle_barrier and not p.slits:
# apply the barrier height to the region around
# the barrier_center within the specified width
V_real += (np.abs(x - p.barrier_center) <
p.barrier_width) * p.barrier_height
if p.middle_barrier and p.slits:
# apply several barriers to the region around
# the barrier_center within the specified width
# allowing therefore slits
for start, end in zip(p.barriers_start, p.barriers_end):
# Ensure correct range regardless of order of start and end
V_real += ((np.abs(x - p.barrier_center) < p.barrier_width) &
(y >= min(start, end)) &
(y <= max(start, end))) * p.barrier_height
...
A fine grid and small time step was chosen to ensure good resolution both in the spatial and temporal dimension. The borders were absorbing so that the wavepacket is crossing the region of interest only once.
p2 = SimpleNamespace(
...
Nx_hr=500, # number of grid points in x direction
Ny_hr=500, # number of grid points in y direction
dt_hr=0.001, # time step for the simulation
...
)
A video of this first step is below.
Accumulation of probability density
Once the simulation of the wavepacket is completed (it takes a few hours) the second step is to compute the probability density at one location (which simulate a screen with photodetectors).
p2 = SimpleNamespace(
...
add_screen=True, # add a screen for show particles collection
screen_data=[[10, -14.95], [10, 14.95], [10.2, 14.95], [10.2, -14.95]], # screen location
load_data=True, # load data from a file
data_folder='data/simul_folder', # folder for data files
...
)
Cells intersection
The data are loaded and cells that are crossed are computed:
def line_cells_crossed(self):
self.crossed_nx = []
self.crossed_ny = []
# Unpack capture data from the global cfg
(x1, y1), (x2, y2) = cfg.capture_data
# Calculate the grid coordinates of the endpoints
x1_idx = int((x1 - self.x_min) // self.dx)
y1_idx = int((y1 - self.y_min) // self.dy)
x2_idx = int((x2 - self.x_min) // self.dx)
y2_idx = int((y2 - self.y_min) // self.dy)
# Bresenham's line algorithm adapted to this grid
cells_crossed = []
seen_cells = set()
dx = abs(x2_idx - x1_idx)
dy = abs(y2_idx - y1_idx)
sx = 1 if x1_idx < x2_idx else -1
sy = 1 if y1_idx < y2_idx else -1
err = dx - dy
x, y = x1_idx, y1_idx
while True:
# Store the actual grid indices
self.crossed_nx.append(x)
self.crossed_ny.append(y)
# compute cell mid point
x_mid = self.x_min + x * self.dx + 0.5 * self.dx
y_mid = self.y_min + y * self.dy + 0.5 * self.dy
cell = (x_mid, y_mid)
if cell in seen_cells:
raise ValueError(f"Duplicate cell detected at {cell}")
seen_cells.add(cell)
cells_crossed.append(cell)
if x == x2_idx and y == y2_idx:
break
e2 = 2 * err
if e2 > -dy:
err -= dy
x += sx
if e2 < dx:
err += dx
y += sy
return len(cells_crossed), cells_crossed
The code tracks which grid cells are intersected by a line segment, representing the path of the wavepacket (or electron) as it passes through the simulation grid.
It adapts Bresenham’s algorithm, which is used for efficient line drawing on a grid. It steps through grid cells between the start and end points, determining which cells the line segment crosses, computes the next grid cell to move to based on the difference between x1_idx and x2_idx (dx) and between y1_idx and y2_idx (dy), as well as the step directions (sx and sy). For each step, it stores the cell indices (self.crossed_nx and self.crossed_ny), along with the midpoint of the cell (x_mid, y_mid).
Finally, there is a check for duplicate cells being crossed using a set (seen_cells). If a duplicate is found, an error is raised to ensure correct detection, as any cell should be crossed at maximum once.
Probability accumulation
Once the cells are known, there is a routine computes and stores the probability density or wavefunction modulus at the detected screen cells for each time snapshot, accumulating the total data for visualization of the interference pattern over time.
def compute(self):
# Initialize the screen_data array
self.screen_data_total = np.zeros(len(self.crossed_nx))
self.screen_data_plot = []
# Loop over each snapshot in psi_plot
for psi in self.wp.psi_plot:
# Reshape the 1D wavefunction array to 2D
psi = psi.reshape(self.Ny, self.Nx)
# initialize a temporary array to accumulate data for this snapshot
temp_data = np.zeros(len(self.crossed_nx))
# loop over each cell in the crossed path
for i, (nx, ny) in enumerate(zip(self.crossed_nx,
self.crossed_ny)):
if cfg.plot_prob:
# calculate the probability density
data = np.abs(psi[ny, nx])**2
else:
# calculate the modulus of the wavefunction
data = np.abs(psi[ny, nx])
# accumulate data for this snapshot
temp_data[i] = data
# Append the snapshot's data to the plot list as a 1D array
self.screen_data_plot.append(temp_data.copy())
# Accumulate this snapshot's data into the total
self.screen_data_total += temp_data
This routine accumulates the probability density (or wavefunction modulus) over time at the grid cells that were identified as being crossed by the electron’s wavepacket. self.screen_data_total: A 1D array initialized to zeros, where each entry corresponds to a cell on the screen. This will store the total accumulated data over all snapshots.self.screen_data_plot: An empty list to store data snapshots for plotting purposes.
The routine iterates through each time snapshot of the wavepacket (psi_plot), which contains the wavefunction at different time steps. The 1D wavefunction data (psi) is reshaped into a 2D grid of size Ny × Nx to match the simulation grid. temp_data: A temporary array initialized to zeros, which holds the accumulated data for each cell on the screen for the current snapshot.
For each identified cell (using the lists self.crossed_nx and self.crossed_ny), the code computes either:
- Probability density (|\psi|^2) if
cfg.plot_probis enabled, or - Modulus of the wavefunction (|\psi|), otherwise.
The computed data is stored in temp_data[i] for the corresponding cell.
After processing all the crossed cells for the current snapshot, the routine appends the snapshot’s data to self.screen_data_plot for plotting. It then adds the snapshot’s data to self.screen_data_total, which accumulates the results over all time steps. The probability is then saved along with the position and will be used to simulate the position of the electrons.
Visualization
Then two routines are responsible for initializing two different types of plots related to the electron wavepacket accumulation on the screen.
def init_plot(self):
dpi = 300 if cfg.high_res_plot else 100
if cfg.fig_4k:
figsize = (3840 / dpi, 2160 / dpi)
else:
figsize = (1920 / dpi, 1080 / dpi)
self.fig, ax = plt.subplots(figsize=figsize, dpi=dpi)
ax.xaxis.set_ticks_position('none')
ax.yaxis.set_ticks_position('none')
# the screen is assumed vertical in the y direction
ax.set_xlim(self.y_min, self.y_max)
ax.set_ylim(0, max(self.screen_data_total) * 1.01)
ax.set_yticklabels([])
ax.set_xticklabels([])
# init the total data
self.screen_data_total_tmp = np.zeros(len(self.crossed_nx))
# Calculate real distances along the y-axis
real_distances = self.y_min + np.array(self.crossed_ny) * self.dy
# Sort by real distances
self.sorted_indices = np.argsort(real_distances)
self.sorted_distances = real_distances[self.sorted_indices]
y0 = np.zeros(len(self.sorted_distances))
self.curve1 = ax.plot(self.sorted_distances, y0, color=c.b,
linestyle="-", linewidth=3)[0]
if cfg.plot_secondary:
self.curve2 = ax.plot(self.sorted_distances, y0, color=c.o,
linestyle="-", linewidth=3)[0]
plt.tight_layout()
The first routine sets up a 1D plot that shows the accumulated probability distribution along the screen (assumed to be vertical in the y-direction).
The resolution and figure size are determined by the cfg.high_res_plot and cfg.fig_4k flags. The higher the resolution, the more detailed the plot (e.g., 4K size or full HD).
self.screen_data_total_tmp is initialized to hold zeroes, which will later be used to accumulate data over time. The y-coordinates (self.crossed_ny) are converted into real distances based on the grid and sorted to ensure a smooth plot.
The sorted distances are plotted against zero values (as a placeholder) using ax.plot and stored in self.curve1. The line represents the accumulated data across the screen.
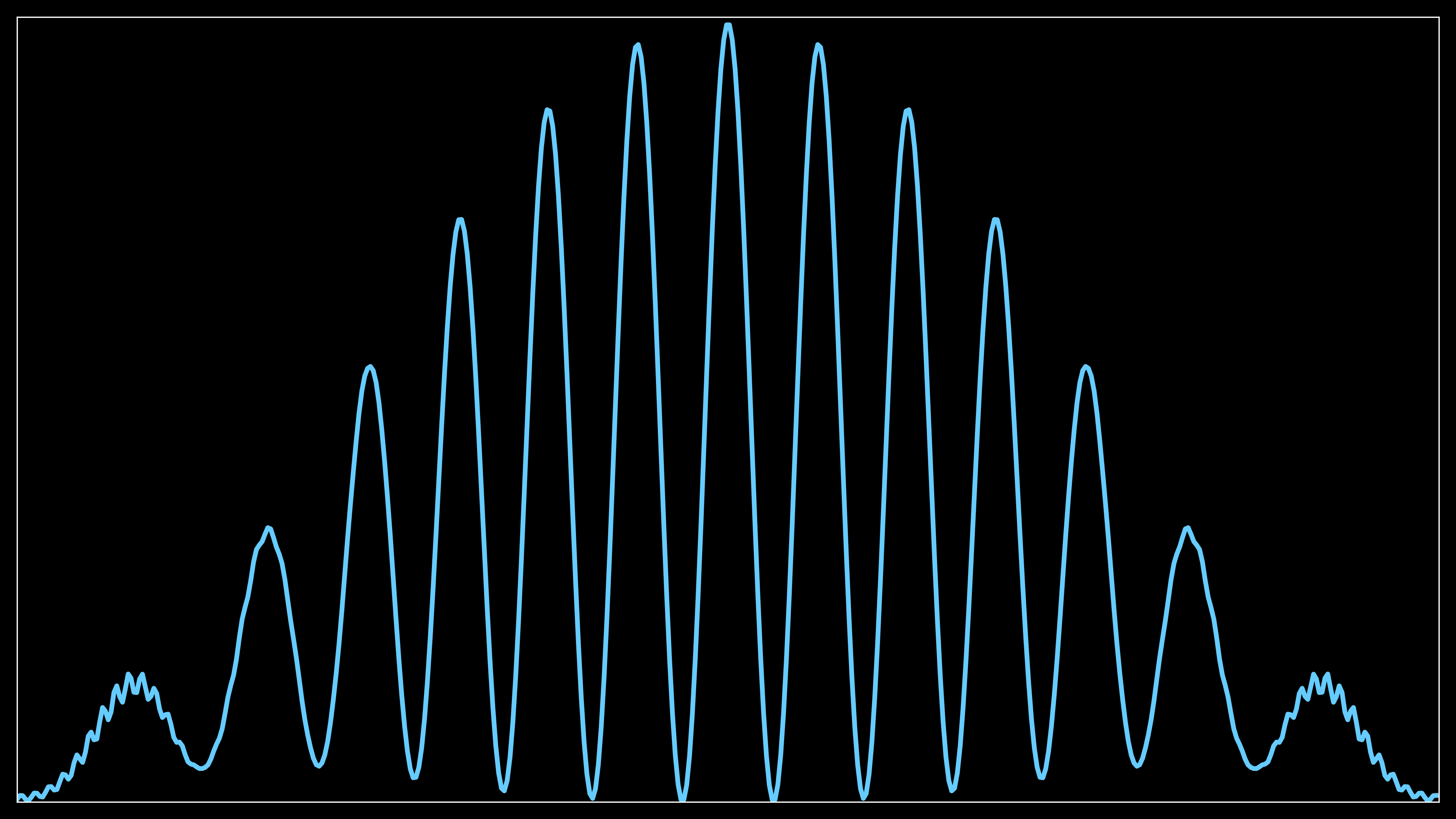
This plot displays the 1D distribution of probability density across the screen, showing how much of the electron wavepacket has been detected at different positions.
def init_plot2(self):
dpi = 300 if cfg.high_res_plot else 100
if cfg.fig_4k:
figsize = (3840 / dpi, 2160 / dpi)
else:
figsize = (1920 / dpi, 1080 / dpi)
self.fig, ax = plt.subplots(figsize=figsize, dpi=dpi)
ax.xaxis.set_ticks_position('none')
ax.yaxis.set_ticks_position('none')
# Convert grid indices to real x and y coordinates
self.crossed_x = [self.x_min + nx * self.dx + 0.5 * self.dx
for nx in self.crossed_nx]
self.crossed_y = [self.y_min + ny * self.dy + 0.5 * self.dy
for ny in self.crossed_ny]
self.curve3 = ax.scatter(self.crossed_x, self.crossed_y,
c=np.zeros_like(self.crossed_x), cmap='hot',
vmin=0, vmax=max(self.screen_data_total))
# the screen is assumed vertical in the y direction
ax.set_xlim(self.x_min, self.x_max)
ax.set_ylim(self.y_min, self.y_max)
ax.set_yticklabels([])
ax.set_xticklabels([])
plt.tight_layout()
The second routine sets up a 2D scatter plot that shows the detected data at the original positions on the simulation grid (representing the actual physical positions on the screen).
Similar to the first routine, the resolution and figure size are set based on configuration flags.
The grid indices of the crossed cells (self.crossed_nx and self.crossed_ny) are converted into real x and y coordinates, creating the actual screen locations where the wavepacket crosses.
The real x and y coordinates are used to create a scatter plot with points representing the detected data. The color of each point is set to 0 initially, and a colormap (hot) is applied to show the intensity (probability) later. The color scale is normalized between 0 and the maximum of self.screen_data_total.
The x and y limits are set to cover the entire simulation grid (from self.x_min to self.x_max and from self.y_min to self.y_max).
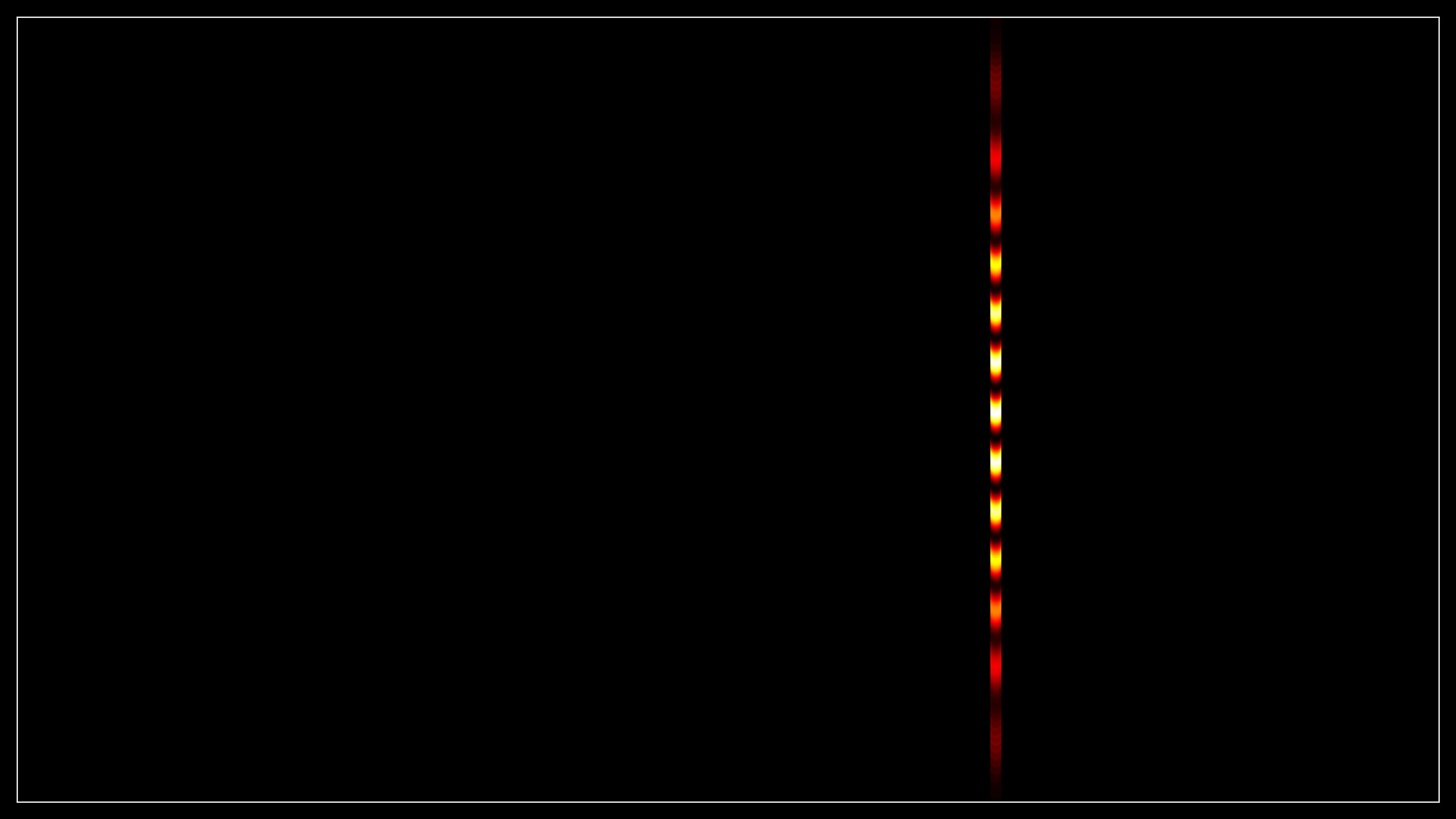
This plot shows a 2D map of where on the screen the electron’s probability density is concentrated, with colors indicating the intensity of the wavepacket at each location.
Finally, an animation of the progressive accumulation is produced, and with ffmpeg the wavepacket propagation is superposed on the top left corner.
Electron beam
The final step is then to simulate the result of the diffraction of an electron beam and the collapse of the wave function leading to point on the screen.
First, the probability distribution is normalized to ensure that the sum equals 1, guaranteeing that each electron will impact the screen according to the correct probability.
...
# normalize perc to make the sum equal to 1
self.probability = [p / sum(doubleslit.screen_data_total)
for p in doubleslit.screen_data_total]
...
Electron position
def compute(self):
# Initialize the screen_data array
self.electrons = []
self.electrons_height = []
self.electrons_count = np.zeros(len(self.probability))
for n in range(int(p.electrons_nb)):
# Randomly choose a bucket based on the probability distribution
bucket = np.random.choice(len(self.probability),
p=self.probability)
# Update the electrons count
self.electrons_count[bucket] += 1
# Keep track of the electron bucket assignment
self.electrons.append(bucket)
# Compute a random height on the electron
height = np.random.uniform(0, 1)
self.electrons_height.append(height)
This routine simulates the process of detecting electrons on a screen based on the normalized probability distribution derived from the wavepacket interference pattern. Few list are created, self.electrons, a list to store which “bucket” (screen region) each electron hits; self.electrons_height, a list to store a random height value for each electron; and self.electrons_count, an array to track how many electrons land in each bucket (region of the screen). It starts as zeros, with a length equal to the number of regions (buckets).
The loop runs p.electrons_nb times, which represents the total number of electrons simulated in the experiment.
For each electron, a bucket (screen region) is randomly chosen using np.random.choice(). The selection is weighted by the normalized self.probability array, which corresponds to the likelihood of an electron landing in each bucket based on the wavepacket’s probability density.
Once a bucket is selected, the count for that bucket is incremented in self.electrons_count to keep track of how many electrons hit that specific region.
The index of the chosen bucket is appended to the self.electrons list, allowing you to trace which bucket each electron was assigned to.
A random height between 0 and 1 is generated for each electron using np.random.uniform(0, 1) and appended to the self.electrons_height list. The reason for the uniform vertical distribution is that, assuming the slit’s vertical size is much larger than the distance between the slits, the diffraction mainly occurs in the plane of the slits. The electron’s height on the screen does not significantly affect the interference pattern, so the vertical distribution is random.
Overall, it simulates the impact of individual electrons on the screen based on the probability density function, and each electron is assigned a random height due to the large vertical extent of the slits.
Visualization
Then two visualization routines are responsible for generating different types of plots for the electron detection simulation.
def init_plot(self):
dpi = 300 if cfg.high_res_plot else 100
if cfg.fig_4k:
figsize = (3840 / dpi, 2160 / dpi)
else:
figsize = (1920 / dpi, 1080 / dpi)
self.fig, ax = plt.subplots(figsize=figsize, dpi=dpi)
ax.xaxis.set_ticks_position('none')
ax.yaxis.set_ticks_position('none')
# the screen is assumed vertical in the y direction
ax.set_xlim(self.y_min, self.y_max)
ax.set_ylim(0, 1.01)
ax.set_yticklabels([])
ax.set_xticklabels([])
# init the total data
# Calculate real distances along the y-axis
real_distances = self.y_min + np.array(self.crossed_ny) * self.dy
# Sort by real distances
self.sorted_indices = np.argsort(real_distances)
self.sorted_distances = real_distances[self.sorted_indices]
self.curve1 = ax.scatter([], [], color=c.b, s=8,
edgecolor=c.k, linewidth=0.2)
plt.tight_layout()
The first routine prepares a scatter plot that will later visualize each individual electron hit on the screen, with random heights (vertical positions) along the y-axis.
The resolution and figure size are determined by the cfg.high_res_plot and cfg.fig_4k flags. The higher the resolution, the more detailed the plot (e.g., 4K size or full HD).
The positions of the cells crossed by the wavepacket are converted to real distances along the y-axis (real_distances) and these distances are sorted to allow the electrons to be plotted in an ordered manner.
A scatter plot (self.curve1) is initialized but starts empty ([] for both x and y coordinates). Electrons will later be plotted progressively in an animation as points with a specific color and point size.
def init_plot2(self):
dpi = 300 if cfg.high_res_plot else 100
if cfg.fig_4k:
figsize = (3840 / dpi, 2160 / dpi)
else:
figsize = (1920 / dpi, 1080 / dpi)
self.fig, ax = plt.subplots(figsize=figsize, dpi=dpi)
ax.xaxis.set_ticks_position('none')
ax.yaxis.set_ticks_position('none')
# the screen is assumed vertical in the y direction
ax.set_xlim(self.y_min, self.y_max)
ax.set_ylim(0, max(self.electrons_count) * 1.01)
ax.set_yticklabels([])
ax.set_xticklabels([])
real_distances = self.y_min + np.array(self.crossed_ny) * self.dy
# Sort by real distances
self.sorted_indices = np.argsort(real_distances)
self.sorted_distances = real_distances[self.sorted_indices]
y0 = np.zeros(len(self.sorted_distances))
self.curve2 = ax.plot(self.sorted_distances, y0, color=c.b,
linestyle="-", linewidth=3)[0]
plt.tight_layout()
The second routine sets up a 1D line plot that shows the accumulated number of electrons hitting different regions on the screen.
Like the first routine, DPI and figure size are adjusted based on configuration flags.
The same calculation for converting grid indices to real distances along the y-axis is performed (real_distances), and the values are sorted to match the order of the detection grid.
A line plot (self.curve2) is initialized to show the electron count as a function of the position along the y-axis.
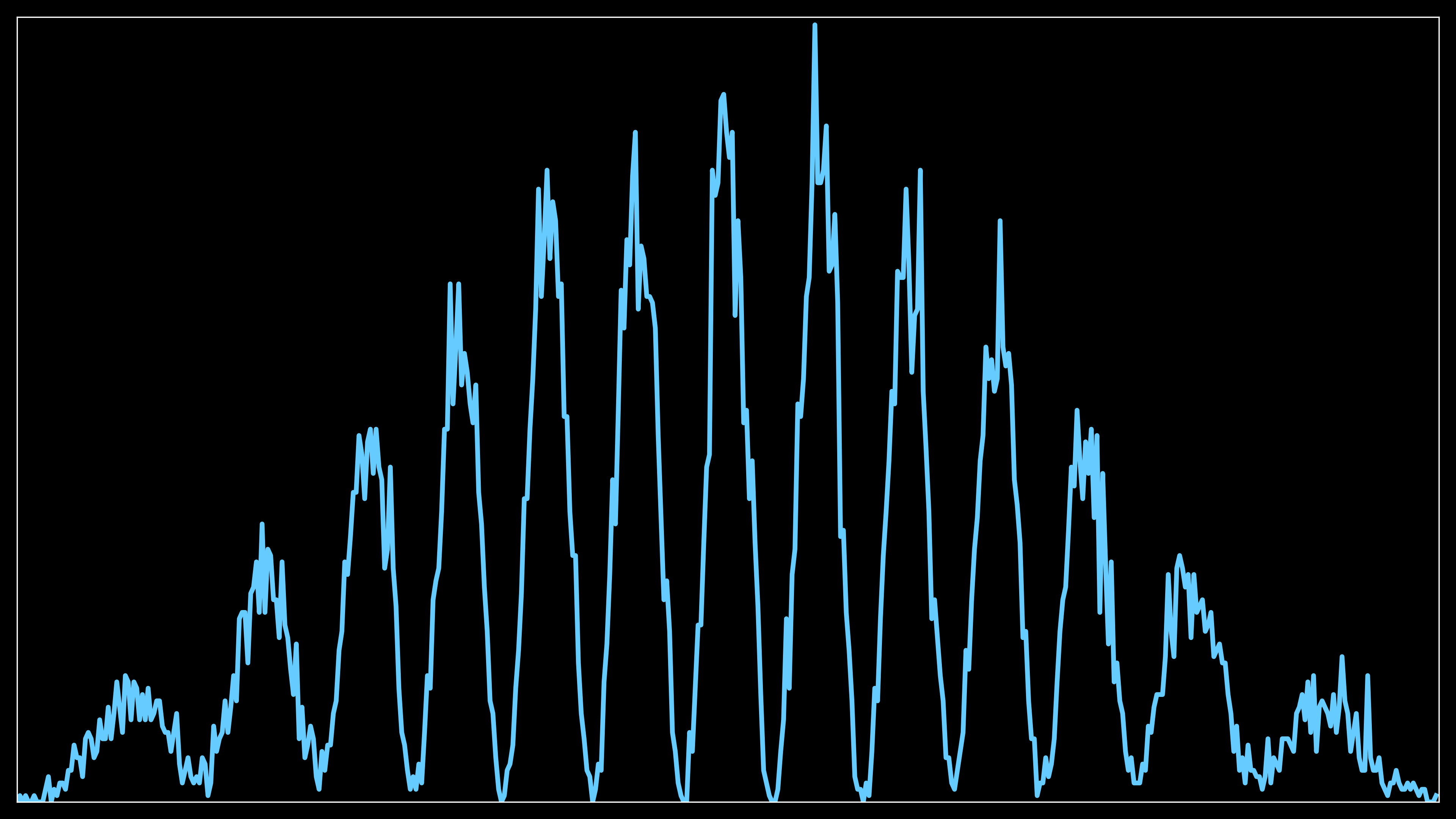
The second plot serves as a verification that the distribution of electrons hitting the screen matches the probability distribution computed in the previous probability accumulation step. By plotting the accumulated electron counts across different regions of the screen, this plot allows you to visually confirm that the interference pattern formed by the electrons reflects the expected probability distribution, ensuring the simulation is correctly following the wavepacket’s computed behavior.
As the number of electrons increases (e.g., from 15,000 to 150,000), the overall interference pattern will not change. However, with more electrons, the fringes will become more sharply defined and concentrated, providing a clearer and more detailed visualization of the interference. The distribution of the electrons remains consistent with the computed probability, but the pattern becomes more precise due to the higher number of data points.
Complete code and results
The complete code and results for the simulation of the electron beam are available on GitHub. The repository contains detailed instructions on how to set up the environment, run the simulations, and visualize the results.
The repository is available at the following link here.