Spin Simulation
Adding complexity with a magnetic field
Introduction
I explore a computational approach to understanding quantum mechanics through the simulation of quantum spins using classical computers. This simulation aims to replicate the behaviors and interactions of quantum particles, specifically their spins, by employing classical computing techniques rather than quantum computing hardware.
Computer setup for simulation
Imagine setting up a classical computer designed to simulate the quantum mechanics of a single spin. The core of the simulation involves instructing the computer to orient a hypothetical spin apparatus in an arbitrary direction. This is done by entering coordinates that define this direction, following which the computer executes an algorithm to resolve the spin’s state.
Objective
The ultimate objective of this simulation is to demonstrate that classical computers, through precise algorithmic design and the use of random number generators, can mimic fundamental quantum behaviors to an extent. This setup allows experimenters to manipulate the simulated system as if they were conducting real quantum mechanical experiments, rotating the measurement apparatus and observing outcomes over varied timescales.
Single spin
Upon receiving the directional coordinates, the computer performs calculations that include leveraging a random number generator to determine the spin’s state, outputting either +1 or -1. This represents the quantum behavior of spin where it can be in an up or down state along the measured axis. The algorithm ensures that if the measurement is repeated immediately, the outcome remains consistent with quantum mechanical principles, demonstrating the same result to simulate quantum state persistence.
In my simulation program, I’ve implemented a flexible system to prepare and measure the state of a quantum spin under different conditions. The program allows for the dynamic setting of the spin’s orientation and the subsequent measurement of its state. Here’s how the dynamics of the simulation are structured:
Spin preparation modes
My program includes several modes for preparing the spin state, each corresponding to a different initial orientation. These modes are designed to reset the spin at each time step to ensure consistent initial conditions for every measurement:
-
Up Direction (Default): The spin is automatically set to the up direction at the start of each time step. This is the default setting, suitable for basic simulations of spin behavior in a controlled quantum state.
-
Left Direction: In this mode, the spin is oriented to the left at each reset. This setting allows exploration of spin dynamics perpendicular to the default plane, providing insights into the behavior under different orientations.
-
Inner Direction: Here, the spin is prepared facing inward, exploring the three-dimensional aspects of quantum spin orientations and their measurements.
-
Collapse on Measurement: The spin state collapses in the direction of the measurement that is performed. This mode mimics the quantum mechanical behavior of spin measurement, where the state vector reduction occurs in the direction of the apparatus alignment.
Simulation interface
Upon launching the program, the interface provides options to orient the measurement apparatus in any desired direction. A dedicated button is available for initiating measurements once the apparatus is aligned. This setup allows for immediate interaction with the spin system, offering a hands-on approach to studying quantum mechanics.
Output details
The results of each measurement session are displayed clearly, providing quantitative insights into the spin behavior:
-
Number of Measurements: The total count of measurements performed during the session is displayed, allowing for statistical analysis of the results over multiple trials.
-
Spin Statistics: The outcomes of the measurements are shown in terms of the percentage of spins aligned in the | +1 \rangle (up) and | -1 \rangle (down) states. This statistical breakdown helps in understanding the probabilistic nature of quantum measurements.
-
Cosine of Half the Angle: The program calculates \cos(\theta_{mn}/2)^2, where \theta_{mn} is the angle between the measurement apparatus orientation and the spin orientation. This calculation is critical as it relates directly to the probability predictions of quantum mechanics for the spin state outcomes based on the angle of measurement.
When analyzing the theoretical results of quantum spin measurements using your simulation, we can consider two specific orientations of the measurement apparatus: along the z-axis and along the x-axis. These predictions are based on the standard quantum mechanical model of spin-½ particles, where the probabilities of outcomes are determined by the square of the cosine and sine of half the angle between the spin’s initial state vector and the measurement apparatus orientation.
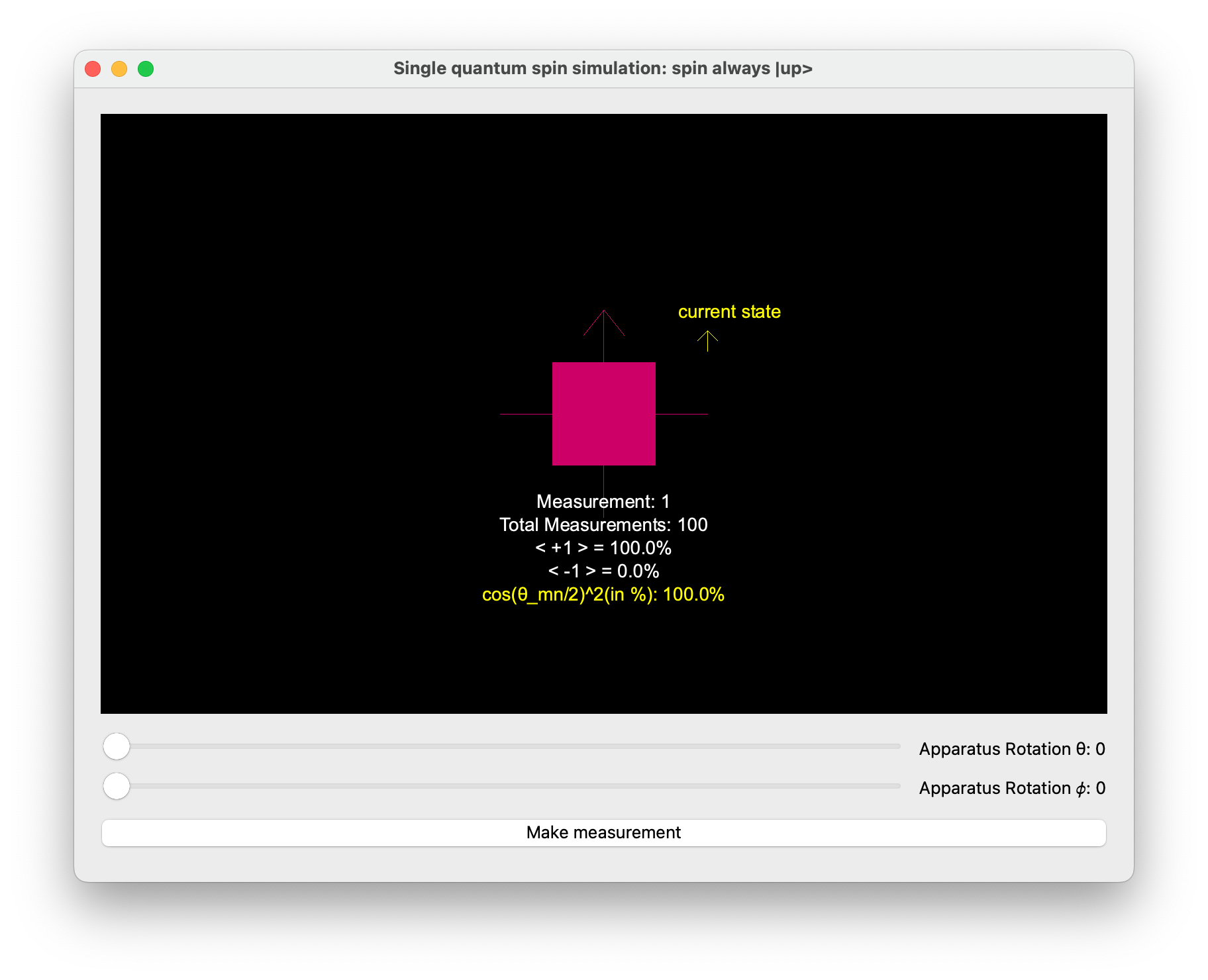
Apparatus Oriented Along the Z-axis (\theta = \phi = 0)
When the apparatus is oriented along the z-axis (\theta = \phi = 0), the measurement directly aligns with the prepared state of the spin if the spin is initially in the up or down direction.
As the spin is prepared in the up direction (| +1 \rangle):
- The probability of measuring the spin in the | +1 \rangle state (spin up) is \cos^2(0/2) = \cos^2(0) = 1.
- The probability of measuring the spin in the | -1 \rangle state (spin down) is \sin^2(0/2) = \sin^2(0) = 0.
- Theoretical result: 100\% probability of observing | +1 \rangle and 0\% probability of observing | -1 \rangle.
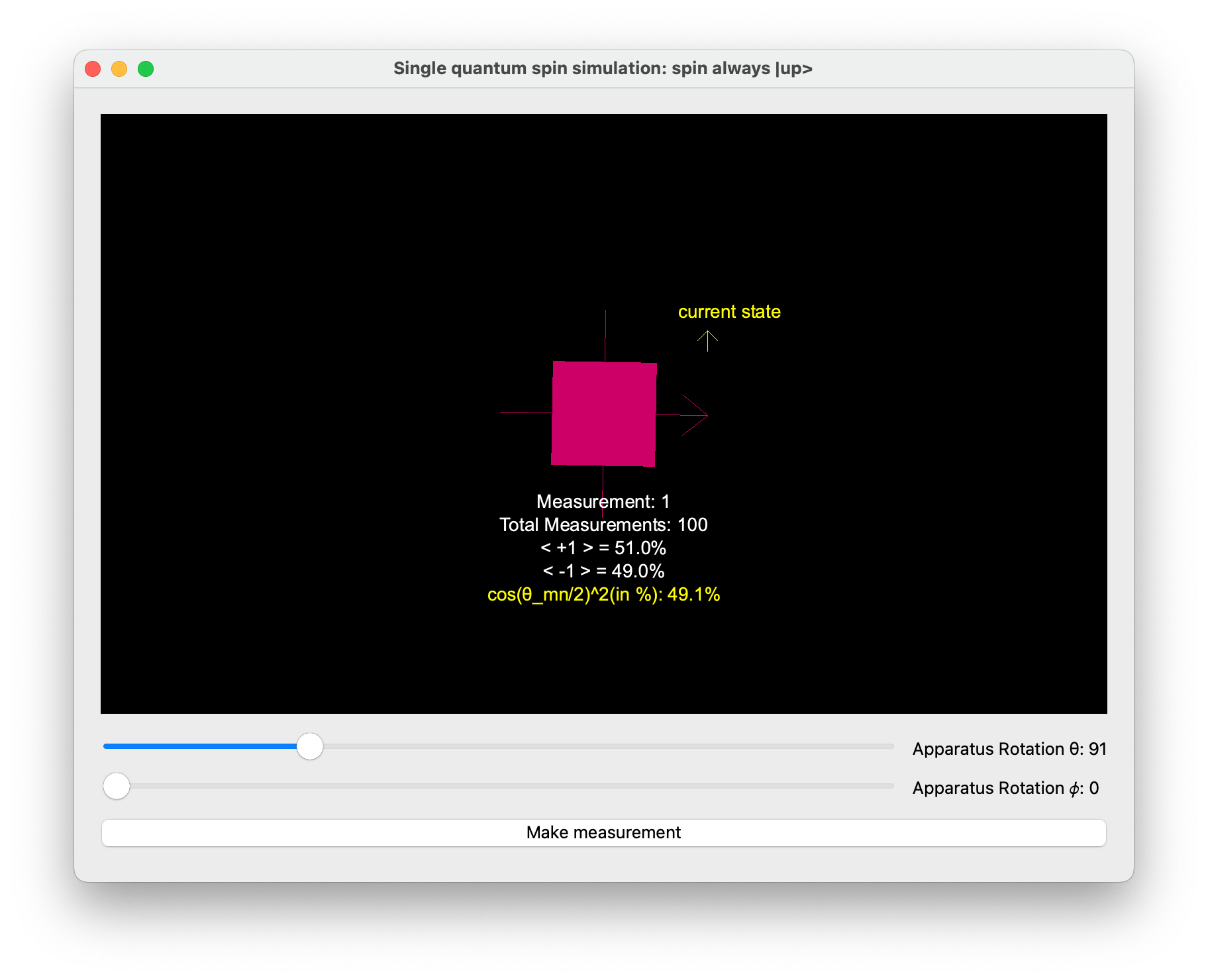
Apparatus Oriented Along the X-axis (\theta = 90^\circ, \phi = 0)
When the apparatus is oriented along the x-axis, it involves a 90° rotation from the z-axis. Here, the spin measurement outcomes are equally probable due to the orthogonal orientation relative to the z-prepared state.
As the spin is prepared in the up direction (| +1 \rangle):
- The probability of measuring the spin in the | +1 \rangle state is \cos^2(\pi/4) = 1/2.
- The probability of measuring the spin in the | -1 \rangle state is \sin^2(\pi/4) = 1/2.
- Theoretical result: 50\% probability of observing | +1 \rangle and 50\% probability of observing | -1 \rangle.
Extension to two spins
Expanding this simulation to two spins introduces additional challenges and complexities. For instance, simulating two spins that are initially connected and then physically separated tests the classical computer’s ability to mimic quantum entanglement and non-locality without maintaining a permanent physical connection between them. This exploration serves to highlight the unique non-local properties of quantum mechanics that classical systems struggle to replicate without continuous direct interaction.
This introduction sets the stage for the technical details and implementation of the simulation, guiding through setting up a simulation environment to replicate and explore these fascinating quantum phenomena using classical computing resources.
Simulation types for two-spin systems
The program offers various predefined states for two spins, with each type intended to simulate specific quantum mechanical properties. Here’s a description of each available simulation type.
1. Product state
Type 1: A = | u \rangle, B = | d \rangle
- This state represents two unentangled spins where spin A is in the up state and spin B is in the down state.
Type 2: A = \frac{1}{\sqrt{2}} (| u \rangle + | d \rangle), B = \frac{1}{2} | u \rangle + \frac{\sqrt{3}}{2} | d \rangle
- This setup involves more complex superpositions for each spin, still unentangled but each in a mixed state, allowing the exploration of probability amplitudes in measurements.
2. Entangled states
Singlet state (type 3): | \Psi \rangle = \frac{1}{\sqrt{2}} (| ud \rangle - | du \rangle)
- The singlet state is a maximally entangled state with anti-correlated spins, meaning if one spin is measured in the up state, the other will always be found in the down state.
Triplet state I (type 4): | \Psi \rangle = \frac{1}{\sqrt{2}} (| ud \rangle + | du \rangle)
- This state is also entangled but with spins being more correlated than in the singlet state.
Triplet state II (type 5): | \Psi \rangle = \frac{1}{\sqrt{2}} (| uu \rangle + | dd \rangle)
- Represents spins that are either both up or both down, showcasing parallel alignment.
Triplet state III (type 6): | \Psi \rangle = \frac{1}{\sqrt{2}} (| uu \rangle - | dd \rangle)
- Another form of the triplet state, similar to Type 5 but with phase differences.
Partially entangled state (type 7): | \Psi \rangle = \sqrt{0.6} | ud \rangle - \sqrt{0.4} | du \rangle
- This state does not have maximal entanglement, allowing examination of non-maximally entangled states’ effects on measurement correlations and outcomes.
Measurement dynamics
Measurements in the two-spin system can be performed independently for each spin or simultaneously to assess correlations:
-
Independent Measurement: When the measurement button for either spin is pressed, only that spin’s state is measured, resetting its status afterward.
-
Simultaneous Measurement: By setting the command-line option
-mor--measure_both(default = False), pressing a measurement button measures both spins simultaneously. This feature is crucial for analyzing the correlation between spins, particularly in entangled states.
Output statistics
The program outputs the measurement results, including:
- The count of measurements for each spin state (| uu \rangle, | ud \rangle, etc.).
- Percentage outcomes for each spin state.
- Calculated correlations for \sigma^z, \sigma^x, and \sigma^y components, which are especially significant for entangled states. For the partially entangled state, hundreds of measurements are necessary to approximate the correct theoretical correlations.
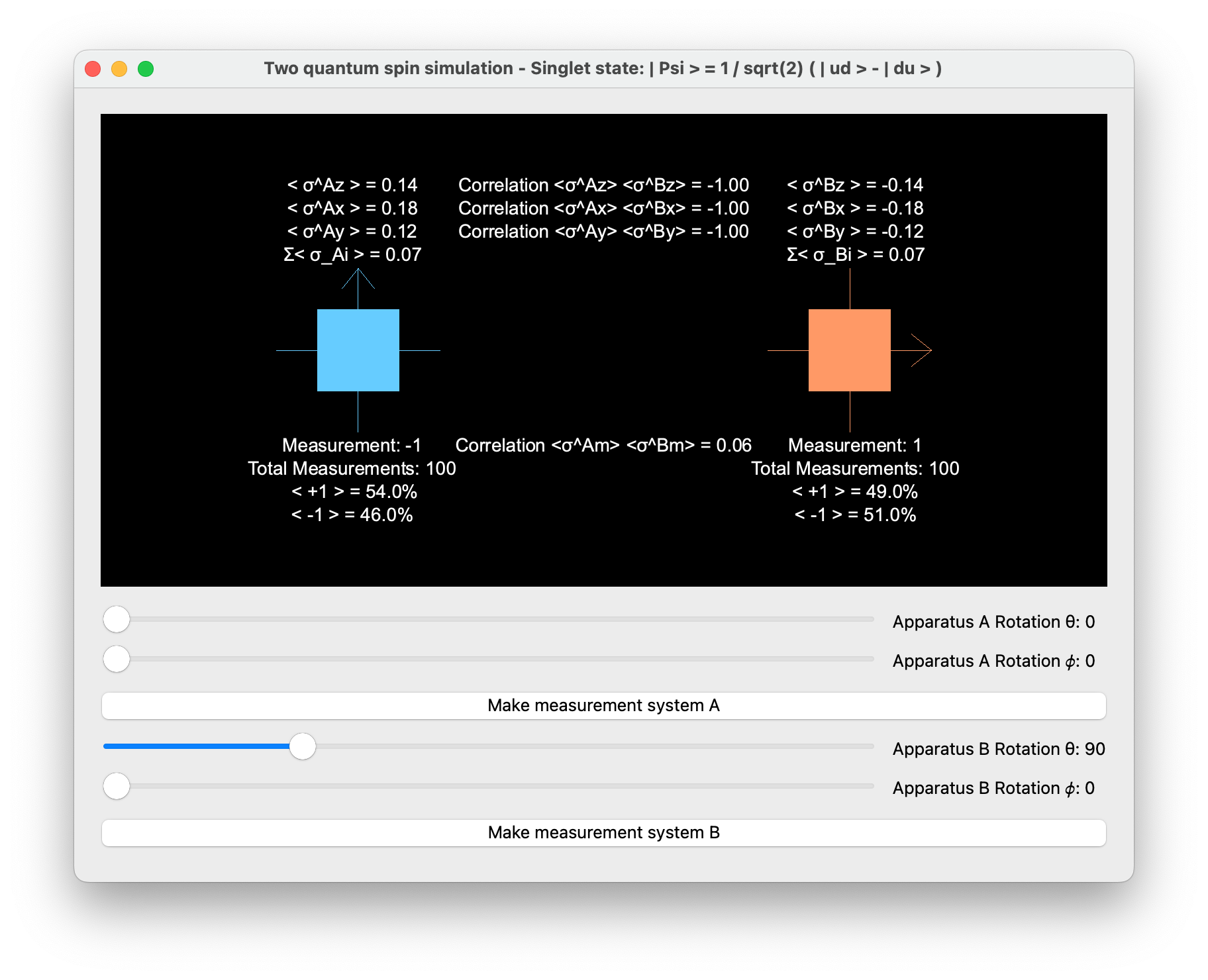
For the two-spin system in the singlet state |\Psi\rangle = \frac{1}{\sqrt{2}} (|ud\rangle - |du\rangle), where each apparatus can be oriented in different directions for measurement, let’s analyze the results for the specified configurations.
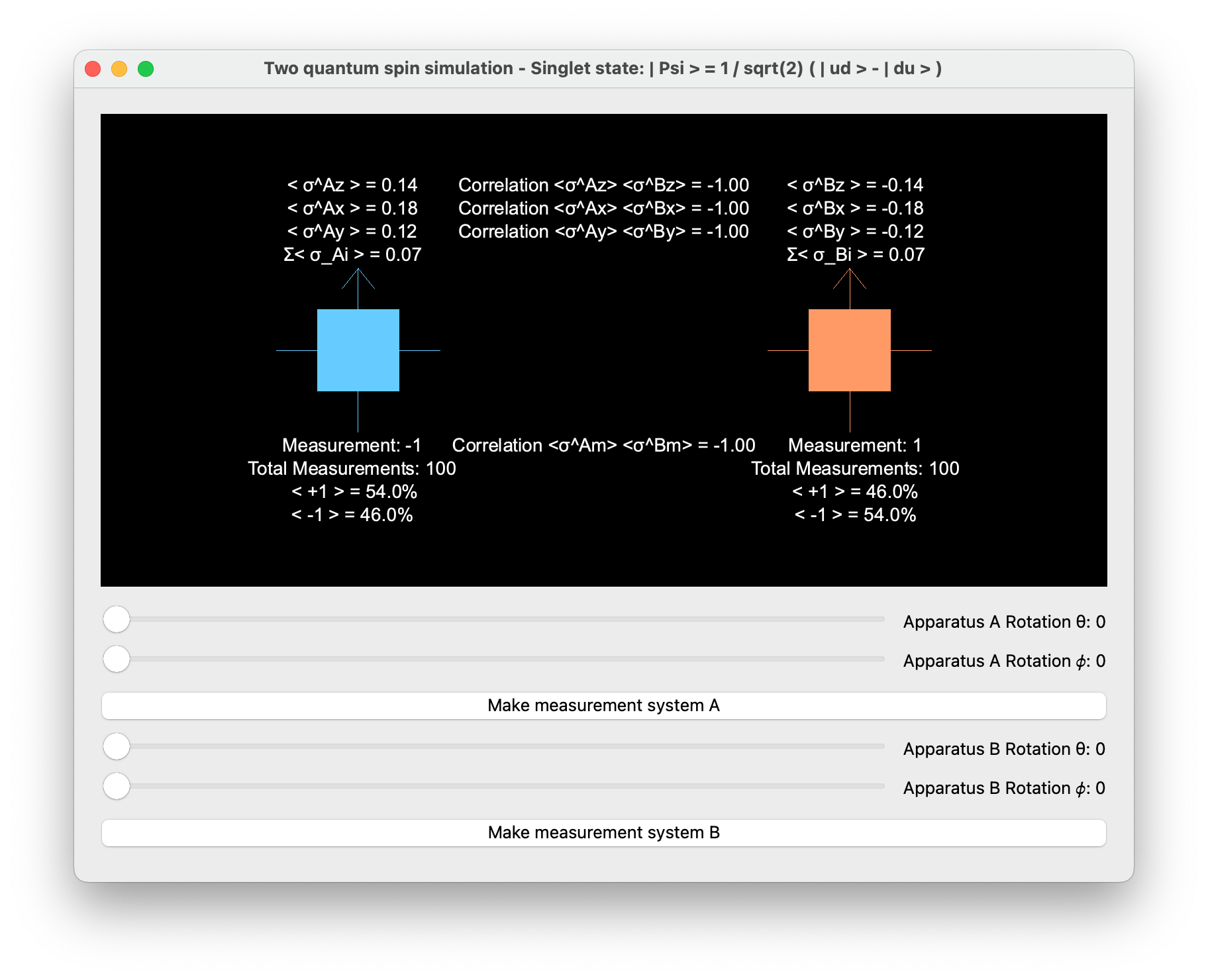
1. Apparatus A & B both in the z positive direction
In this configuration, both A and B are aligned along the z-axis in the positive direction.
- Probability P_A to measure +1: 50\%
- Probability P_B to measure +1: 50\%
- Correlation between A and B measurements: -1
The singlet state is anti-correlated, so if A measures spin up (|+1\rangle), B will always measure spin down (|-1\rangle), and vice versa. Thus, the correlation (expectation value of the product of measurements) is -1, indicating perfect anti-correlation.
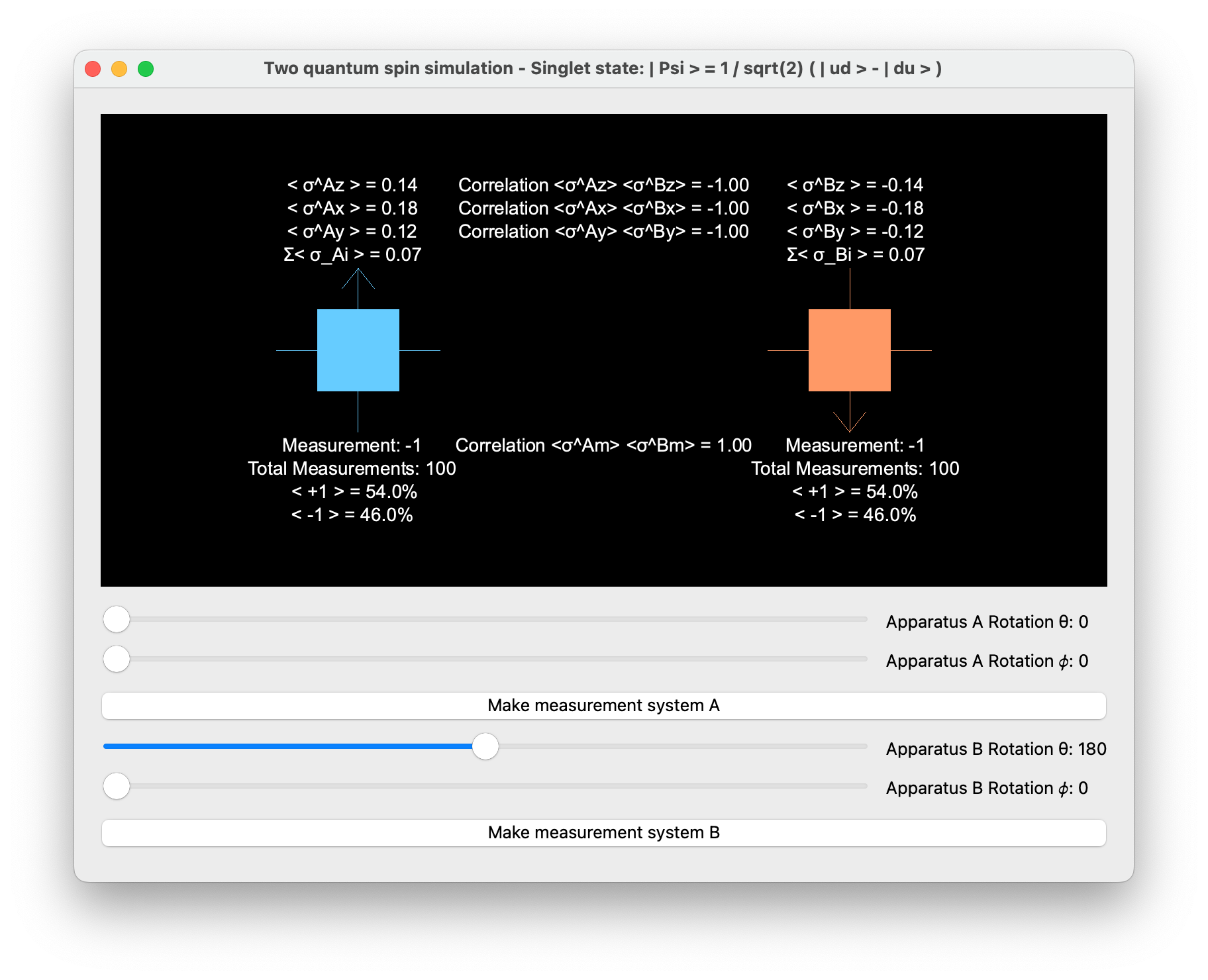
2. Apparatus A positive z, apparatus B negative z
In this case, A is aligned along the positive z-axis, and B is aligned along the negative z-axis.
- Probability P_A to measure +1: 50\%
- Probability P_B to measure +1: 50\%
- Correlation between A and B measurements: +1
Since the spins are anti-correlated in the singlet state, measuring A in the positive direction and B in the opposite direction will yield opposite outcomes. If A is |+1\rangle, B being aligned in the negative direction will measure the spin as |+1\rangle (opposite of its actual state), leading to a correlation of +1.
3. Apparatus A Positive z, apparatus B x direction
Here, A is aligned along the z-axis, and B is along the x-axis.
- Probability P_A to measure +1: 50\%
- Probability P_B to measure +1: 50\%
- Correlation between A and B measurements: 0
When measuring spin in orthogonal directions (A in z and B in x), the measurements are uncorrelated. The quantum mechanical prediction for spins measured in orthogonal directions in a singlet state is that their outcomes will be completely random and independent. Therefore, the correlation between A and B in this configuration is 0.
These configurations and results illustrate how the quantum mechanical properties of entanglement and the orientation of measurement apparatus impact the outcomes in predictable and fascinating ways.
Practical use
This simulation serves as an educational tool for demonstrating and teaching the fundamental principles of quantum mechanics. By manipulating the orientation of the apparatus and observing the corresponding changes in spin measurement outcomes, users can gain a practical understanding of concepts such as quantum state superposition and collapse, and the impact of observer measurement on a quantum system.
This dynamic approach, combined with direct control over spin preparation and measurement, provides a comprehensive platform for exploring and validating the theoretical underpinnings of quantum spin dynamics using classical computational methods.
Adding complexity with a magnetic field
To increase the realism and complexity of the simulation, a mathematical model of a magnetic field could be introduced. This addition would allow the spin to undergo precession, mimicking more closely the dynamic behavior of real quantum systems. Here, the computer solves the Schrödinger equation to determine the temporal evolution of the spin’s state and calculates the probabilities of finding the spin in either the up or down state at any given time.
References
SUSSKIND, Leonard, 2015. Quantum Mechanics - The Theoretical Minimum. London: Penguin Books Ltd. ISBN 978-0-14-197781-2.