Quantum Harmonic Oscillator - Time evolution
In the context of quantum mechanics, the concept of a harmonic oscillator extends the principles observed in the “particle in a box” model, introducing oscillatory behavior in quantum systems. A fundamental approach to explore these phenomena involves examining the superposition of the initial two energy eigenstates. This approach is straightforward and provides an accessible means to understand quantum oscillations.
When dealing with superpositions, a linear combination of two energy eigenstates, each with energies E_a and E_b, results in a probability distribution that exhibits oscillation. The oscillation occurs at an angular frequency defined by the difference in energies (E_a - E_b) divided by \hbar, where the absolute value ensures a positive frequency. This frequency determines the oscillation rate of the system.
Considering a superposition wave function composed of two spatial functions, each associated with a specific energy and coefficient (c_a and c_b), leads to a linear superposition of states. The resultant probability distribution includes terms for the individual probabilities modified by c_a^2 and c_b^2, alongside an oscillating term that reflects the energy difference through the frequency \frac{E_a - E_b}{\hbar}.
So, if there is a superposition wavefunction:
\Psi_{ab}(\mathbf r, t) = c_a e^{-i\frac{E_a}{\hbar}t} \psi_a(\mathbf r) + c_b e^{-i\frac{E_b}{\hbar}t} \psi_b(\mathbf r) then the probability density is:
\left|\Psi_{ab}(\mathbf r, t)\right|^2 = \left|c_a\right|^2\left|\psi_a(\mathbf r)\right|^2 + \left|c_b\right|^2\left|\psi_b(\mathbf r)\right|^2 + 2\left| \overline{c_a\psi_a(\mathbf r)}c_b\psi_b(\mathbf r) \right| \cos\left[\frac{\left(E_a-E_b\right)}{\hbar}-\theta_{ab}\right]
where:
\theta_{ab} = \arg\left(c_a\psi_a(\mathbf r)\overline{c_b\psi_b(\mathbf r)} \right)
In the case of the harmonic oscillator, the time-independent solutions are:
\begin{aligned} & \psi_n(\xi) = \sqrt{\frac{1}{\sqrt \pi 2^n n!}} e^{-\frac{\xi^2}{2}}H_n(\xi) \\ & E_n = \left(n + \frac{1}{2}\right)\hbar\,\omega, \quad n \in \mathbb N \end{aligned}
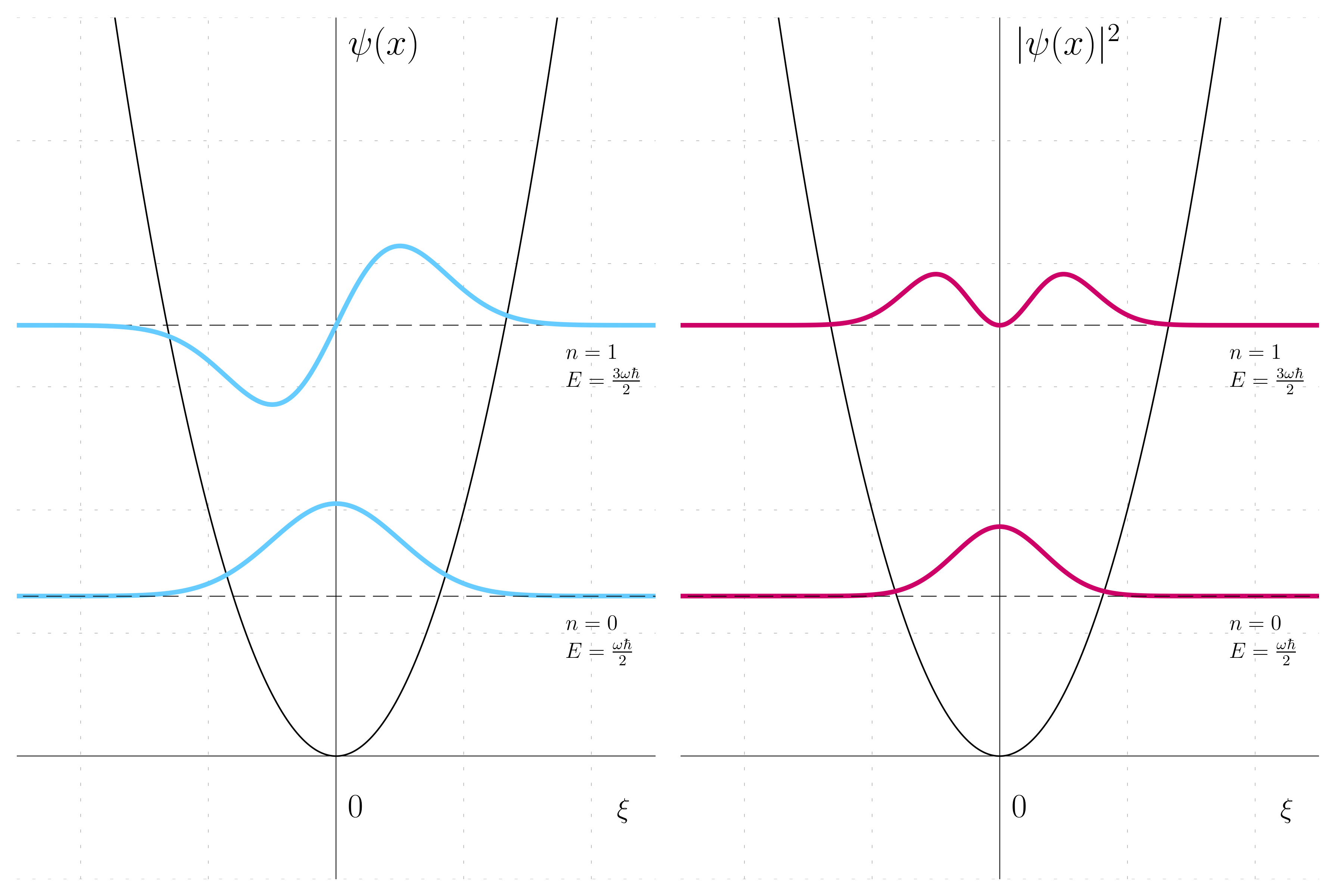
Where \omega is the the oscillation frequency, the angular oscillation frequency of the classical oscillator with the same potential. Considering now the first two states, for n = 0:
\begin{aligned} & \psi_0(\xi) = \sqrt{\frac{1}{\sqrt{\pi}}} e^{-\frac{\xi^2}{2}}H_0(\xi) \\ & E_0 = \frac{1}{2}\hbar\omega \end{aligned}
For n = 1:
\begin{aligned} & \psi_1(\xi) = \sqrt{\frac{1}{2\sqrt{\pi}}} e^{-\frac{\xi^2}{2}}H_1(\xi) \\ & E_1 = \frac{3}{2}\hbar\omega \end{aligned}
The wave function and the probability density for these two states are as in the below picture:
Then the time-dependent solution for each of two states is given multiplying the eigenstate by the time dependent factor:
\begin{aligned} \Psi_0(x,t) & = e^{-i\frac{E_0}{\hbar}t}\psi_0(x) \\ \Psi_1(x,t) & = e^{-i\frac{E_1}{\hbar}t}\psi_1(x) \end{aligned}
When adding these two solution in a superposition, at that point the probability density is having an oscillating motion.
The graphs depict the superposed wavefunction’s real (\Re\{\Psi(x,t)\}) and imaginary (\Im\{\Psi(x,t)\}) parts as a function of time t on the left, each plotted at different heights for clarity. On the right, the probability density (|\Psi(x,t)|^2) is shown, illustrating how the wavefunction’s magnitude squared varies over time.
This give the oscillating motion with period \omega = \frac{E_1-E_0}{\hbar} = \frac{2E_0}{\hbar}, which is, in this case, also the frequency of the classical harmonic oscillator, with the same potential.
At last seen the harmonic oscillator is oscillating with the expected frequency, the frequency of the classical harmonic oscillator with the same potential energy function.
However, this behavior we are seeing here is still not very close to what is seen in a classical harmonic oscillator. There is some additional parts that need to be considered.
The coherent state
We’ve observed oscillatory behavior in both the particle in a box and the quantum harmonic oscillator. However, the quantum harmonic oscillator hasn’t closely mirrored the dynamics of a classical harmonic oscillator yet, lacking a singular, smooth-moving probability distribution. While the probability distribution did shift from one side to the other, it exhibited irregularities and shape changes during oscillation. This observation is based on a simplistic linear superposition of the first two energy levels of the harmonic oscillator, noting the potential for more complex superpositions.
The coherent state stands out for its intriguing connection between quantum and classical dynamics, a concept initially explored by Schrödinger in 1926. This state’s formal mathematical framework, developed in the 1960s by Roy Glauber, is integral to the quantum mechanical understanding of lasers and coherent light. Our approach involves examining a specific linear superposition and its behavior. Remarkably, increasing the energy within this coherent state gradually reveals dynamics akin to those of a classical harmonic oscillator, thereby identifying a quantum mechanical state that mirrors classical behavior.
The coherent state for a harmonic oscillator with frequency \omega is a linear superposition of harmonic oscillator wave functions:
\Psi_n(\xi,t) = \sum_{n=0}^\infty c_n e^{-i\left(n + \frac{1}{2}\right)\omega\,t}\psi_n(t)
Each wave function is multiplied by its respective time-dependent exponential factor, e^{-iE_n/\hbar t}, where E_n = (n + \frac{1}{2})\hbar\omega represents the energy of the n^{th} state, and \hbar is the reduced Planck’s constant. The sum extends from n=0 to infinity, incorporating a specific set of coefficients with two indices: one for the harmonic oscillator state (n) and another for a parameter (N), differentiating the coherent states.
The parameter N is chosen to define the coherent state, while n indexes the particular harmonic oscillator state. These coefficients are determined by a given formula for each harmonic oscillator state (n) and the selected value of N. This number is not constrained to be an integer, it can take any real value.
The coefficients obey the following formula:
c_n = \sqrt{\frac{N^ne^{-N}}{n!}}
As a curiosity |c_n|^2 is a Poisson distribution from statistics, with a mean N and a standard deviation \sqrt N. It will not be used in the harmonic oscillator but it explains for example the distribution of the arrival of photons in a laser beam, that in an ideal form are in a coherent state, obeys this distribution.
Observing oscillations within the coherent state, utilizing the previously established coefficients and harmonic oscillator eigenstates with appropriate time-dependent factors, we focus on a scenario where the parameter N is set to 1.
This results in a probability density that oscillates back and forth, maintaining its shape and displaying a sinusoidal oscillation. The parameter N need not be an integer; it can be any real number, though integers are used in this instance.
Despite the clear oscillation, the particle doesn’t occupy a precise position, as evidenced by the considerable width of the distribution. However, the consistency of its shape throughout the oscillation aligns more closely with classical oscillatory behavior.
When adjusting this parameter, we observe a more concentrated distribution, still oscillating at the same rate. As we alter both horizontal and vertical scales, the oscillation for N=10 is broader compared to N=1. This parameter, N, eventually represents the total energy in our oscillator or coherent state. It becomes significantly more focused, with both scales expanding due to the distribution’s spatial narrowing. Despite this narrowing, the overall area remains constant, ensuring normalization, leading to taller peaks as the distribution tightens.
Moving to N=75, the oscillation’s amplitude and the distribution’s sharpness increase, signaling a shift towards classical oscillator behavior. This narrow distribution and the particle’s back-and-forth sinusoidal motion highlight the coherent state’s ability to mimic a classical oscillating particle.
This coherent state, though initially arbitrary, demonstrates that quantum mechanics can replicate classical oscillation patterns, establishing a link from quantum to classical physics. However, quantum mechanics allows for various superpositions not directly analogous to classical phenomena, presenting one of its mysteries: why classical-like states are more commonly observed than their non-classical counterparts.
In summary, for a harmonic oscillator in a coherent state, the probability distribution oscillates across the potential with a consistent shape, narrowing spatially with higher N values. Large N results in a localized distribution relative to the oscillation’s size, mirroring classical oscillation concepts. The coherent state, a special superposition of eigenstates, uniquely reflects the classical harmonic oscillator’s behavior. Unlike this specific case, general superpositions don’t exhibit simple harmonic motion unless energy levels are equally spaced or maintain specific ratios, a characteristic inherent to harmonic oscillators.