Particle in a box - Time evolution
In this segment, I continue my exploration of the quantum mechanical model of a particle confined in a one-dimensional box, a topic I have previously introduced in a preceding article. My current discussion explores the intricate time evolution of a quantum system, specifically focusing on a particle trapped within a rigid box with infinitely high potential barriers at the boundaries. This scenario is emblematic of the “particle in a box” model, a concept in quantum mechanics that provides profound insights into the behavior of particles at the quantum level.
If you’re just joining me, I highly recommend reviewing the earlier piece to establish a solid understanding of the principles underlying the quantum confinement and the quantization of energy levels. The initial article laid the groundwork by describing the spatial quantization and stationary states of a particle confined in such a potential well, setting the stage for the complex dynamics we’re about to explore. To fully appreciate the nuances of the time evolution of quantum states, please ensure you’re familiar with the concepts discussed here.
Considering the same potential V(x) such as:
V(x) = \begin{cases} 0 & \quad 0 \le x \le L \\ \infty & \quad x < 0, x > L\end{cases}
In this follow-up, I extend the discussion to include the time-dependent aspects of the quantum system. Specifically, I examine a particle initially in a superposition of the first two quantum states within the box and its subsequent temporal evolution:
\begin{aligned} \Psi(x, t) & = \frac{1}{\sqrt{L}} \left[ c_1 \sin\left(\frac{\pi x}{L}\right) e^{-i \frac{\pi^2 \hbar}{2mL^2} t} + c_2 \sin\left(\frac{2\pi x}{L}\right) e^{-i \frac{4\pi^2 \hbar}{2mL^2} t} \right]\\ & = \frac{1}{\sqrt{L}} \left[ c_1 \sin\left(\frac{\pi x}{L}\right) e^{-i \frac{E_1}{\hbar} t} + c_2 \sin\left(\frac{2\pi x}{L}\right) e^{-i \frac{E_2}{\hbar} t} \right] \end{aligned}
It worth noting that for each of these eigenfunctions in the superposition, they are multiplied it by its appropriate complex exponential time-varying function, and also that this superposition has been normalized.
The normalization is
\begin{aligned} \int_{-\infty}^\infty |\Psi(x,t)|^2 \mathrm dx & = \int_{-\infty}^\infty |\Psi(x,0)|^2 \mathrm dx = \int_0^L |A|^2 \left(\overline {\psi_1(x)} + \overline {\psi_2(x)} \right) \left(\psi_1(x) + \psi_2(x) \right) \mathrm dx \\ & = \int_0^L |A|^2 \frac{2}{L}\left\{\left[ \sin\left(\frac{\pi}{L}x\right) + \sin\left(\frac{2\pi}{L}x\right)\right]\left[ \sin\left(\frac{\pi}{L}x\right) + \sin\left(\frac{2\pi}{L}x\right)\right]\right\}\mathrm dx \\ & = |A|^2 \frac{2}{L} \int_0^L \left[ \sin^2\left(\frac{\pi}{L}x\right) + 2\sin\left(\frac{\pi}{L}x\right)\sin\left(\frac{2\pi}{L}x\right) + \sin^2\left(\frac{2\pi}{L}x\right) \right]\mathrm dx \\ & = |A|^2 \frac{2}{L} \int_0^L \left[ \sin^2\left(\frac{\pi}{L}x\right) + \sin^2\left(\frac{2\pi}{L}x\right) \right]\mathrm dx \\ & = |A|^2 \frac{2}{L} \left[ \frac{x}{2} - \frac{1}{4\pi}\sin\left(\frac{\pi}{L}x\right) + \frac{x}{2} - \frac{1}{8\pi}\sin\left(\frac{2\pi}{L}x\right) \right]\bigg|_0^a \\ & |A|^2 \frac{2}{L}a = |A|^2 \frac{1}{2} = 1 \end{aligned}
as \sin\left(\frac{\pi}{L}x\right) and \sin\left(\frac{2\pi}{L}x\right) are orthogonal and their product is 0; therefore:
A = \frac{1}{\sqrt 2}
and the wave function at t=0 is:
\Psi(x,0) = \frac{1}{\sqrt 2}\left(\psi_1(x) + \psi_2(x) \right) = \frac{1}{\sqrt L}\left[ \sin\left(\frac{\pi}{L}x\right) + \sin\left(\frac{2\pi}{L}x\right)\right]
the general solution it is then:
\Psi(x,t) = \frac{1}{\sqrt L} \left[ \sin\left(\frac{\pi}{L}x\right)e^{-i \frac{\hbar \pi^2}{2ma^2}t} + \sin\left(\frac{2\pi}{L}x\right)e^{-i \frac{\hbar 4\pi^2}{2ma^2}t} \right] = \frac{1}{\sqrt L} \left[ \sin\left(\frac{\pi}{L}x\right)e^{-i \omega t} + \sin\left(\frac{2\pi}{L}x\right)e^{-4i \omega t} \right]
where:
\omega \equiv \frac{\hbar \pi^2}{ma^2}
Then |\Psi(x,t)|^2:
\begin{aligned} |\Psi(x,t)|^2 = & \overline {\Psi(x,t)} \Psi(x,t) =\frac{1}{L} \left\{\left[ \sin\left(\frac{\pi}{L}x\right)e^{i \omega t} + \sin\left(\frac{2\pi}{L}x\right)e^{4i \omega t} \right] \left[ \sin\left(\frac{\pi}{L}x\right)e^{-i \omega t} + \sin\left(\frac{2\pi}{L}x\right)e^{-4i \omega t} \right]\right\} \\ = & \frac{1}{L} \left[ \sin^2\left(\frac{\pi}{L}x\right) + \sin\left(\frac{\pi}{L}x\right)e^{i \omega t}\sin\left(\frac{2\pi}{L}x\right)e^{-4i \omega t} + \sin\left(\frac{2\pi}{L}x\right)e^{4i \omega t} \sin\left(\frac{\pi}{L}x\right)e^{-i \omega t} + \sin^2\left(\frac{2\pi}{L}x\right)\right] \\ = & \frac{1}{L} \left[ \sin^2\left(\frac{\pi}{L}x\right) + \sin^2\left(\frac{2\pi}{L}x\right) + \sin\left(\frac{\pi}{L}x\right) \sin\left(\frac{2\pi}{L}x\right) \left(e^{3i \omega t} + e^{-3i \omega t}\right) \right]\\ = & \frac{1}{L} \left[ \sin^2\left(\frac{\pi}{L}x\right) + \sin^2\left(\frac{2\pi}{L}x\right) + 2 \sin\left(\frac{\pi}{L}x\right) \sin\left(\frac{2\pi}{L}x\right) \cos(3\omega t) \right] \end{aligned}
As:
\begin{aligned} e^{3i \omega t} + e^{-3i \omega t} = & \cos(3 \omega t) + i\sin(3 \omega t) + \cos(-3 \omega t) + i\sin(-3 \omega t) \\ = & \cos(3 \omega t) + i\sin(3 \omega t) + \cos(3 \omega t) - i\sin(3 \omega t) = 2\cos(3 \omega t) \end{aligned}
This probability density has an oscillating part in time, at an angular frequency:
3\omega = 3\frac{\hbar \pi^2}{ma^2} = \frac{3E_1}{\hbar} = \frac{E_2 - E_1}{\hbar}
The absolute energy origin is not important, only the difference E_2 - E_1 and this is often happening in quantum mechanics.
As a reminder, the wave function and the probability density for these two states are as in the below picture:
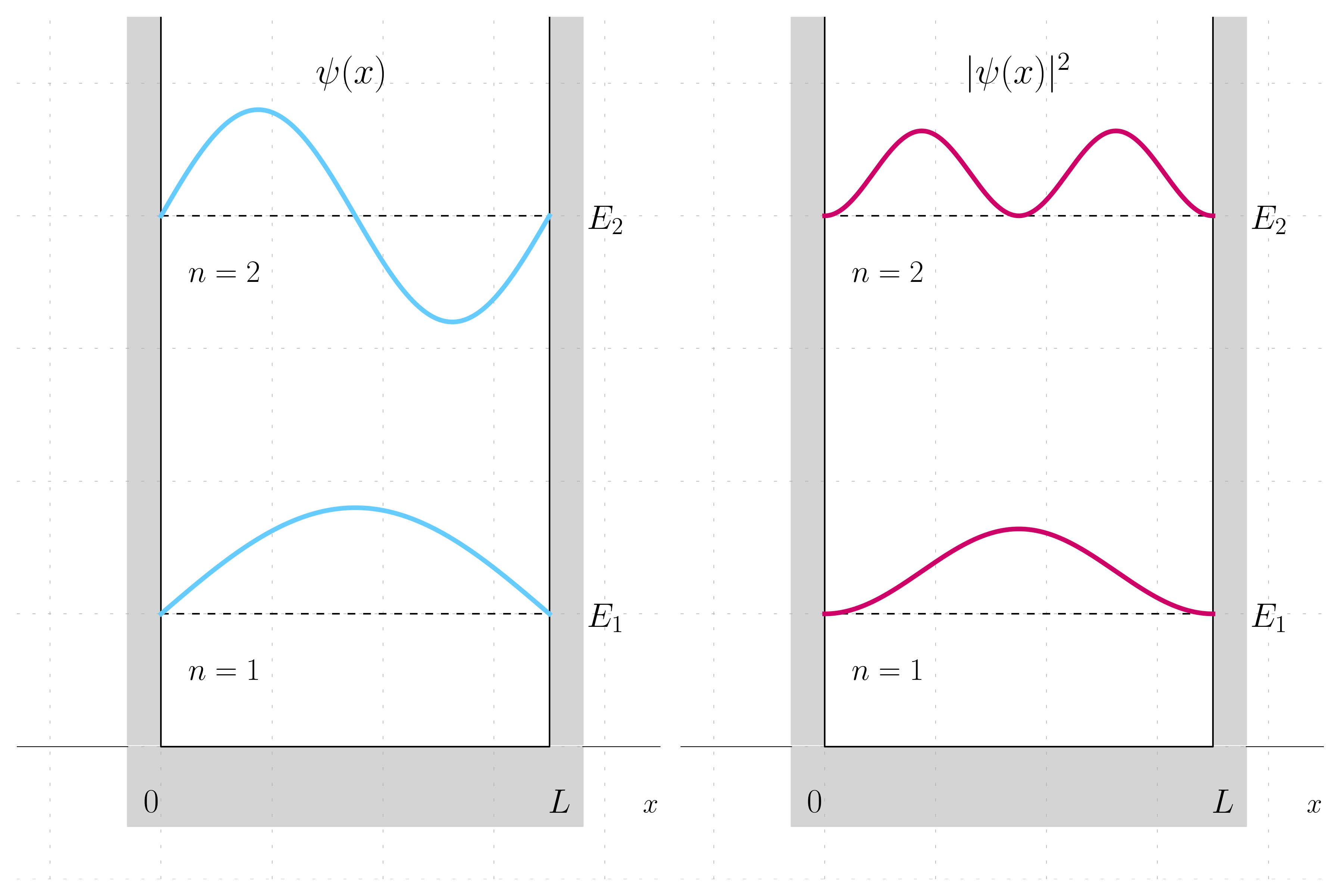
Then the time-dependent solution for each of two states is given multiplying the eigenstate by the time dependent factor:
\begin{aligned} \Psi_1(x,t) & = e^{-i\frac{E_1}{\hbar}t}\psi_1(x) \\ \Psi_2(x,t) & = e^{-i\frac{E_2}{\hbar}t}\psi_2(x) \end{aligned}
For each state, the probability density is not changing:
\begin{aligned} P(1) & = \left| \Psi_1(x,t) \right|^2 = e^{i\frac{E_1}{\hbar}t}\overline{\psi_1(x)} e^{-i\frac{E_1}{\hbar}t}\psi_1(x) = \overline{\psi_1(x)} \psi_1(x) = |\psi_1(x)|^2 \\ P(2) & = \left| \Psi_2(x,t) \right|^2 = e^{i\frac{E_2}{\hbar}t}\overline{\psi_2(x)} e^{-i\frac{E_2}{\hbar}t}\psi_2(x) = \overline{\psi_2(x)} \psi_2(x) = |\psi_2(x)|^2 \end{aligned}
The time factor is not contributing to the density, as these wavefunctions are still solutions of the time-independent Schrödinger equation.
When adding these two solution in a superposition, at that point the probability density is having an oscillating motion, because it is:
P(s) = \left| \Psi_2(x,t) + \Psi_2(x,t) \right|^2
The two solution are first added, then squared.
The graphs depict the superposed wavefunction’s real (\Re\{\Psi(x,t)\}) and imaginary (\Im\{\Psi(x,t)\}) parts as a function of time t on the left, each plotted at different heights for clarity. On the right, the probability density (|\Psi(x,t)|^2) is shown, illustrating how the wavefunction’s magnitude squared varies over time.
This give the oscillating motion with period \omega_{21} = \frac{3E_1}{\hbar}. In this scenario, we’re observing a particle oscillating within a potential well, demonstrating time-dependent behavior. This is illustrated through the probability density’s variation with position x inside the well, showcasing the particle’s oscillatory motion. Quantum mechanics allows us to understand such dynamic systems.
In the current case, the particle’s motion results from being in a superposition of the well’s first and second states—where the first state has a single peak in the center and the second state has two peaks on either side.
Individually, these states have stationary probability densities. However, in quantum mechanics, we combine the wave functions (quantum mechanical amplitudes) of these states first and then compute the probability density by taking the squared modulus of the sum, which reveals the oscillatory behavior rather than a stationary distribution.