Yukawa Potential
In classical mechanics, the motion of celestial bodies is typically described by Newtonian gravity, with the potential energy given by U(r) = -\frac{GMm}{r}. However, it is possible to consider other forms of central forces. For example, a potential of the form (Yukawa potential):
U(r) = \frac{K_1}{r} e^{-\frac{\left\|\mathbf{r}_2 - \mathbf{r}_1\right\|}{K_2}}
where K_1 = GmM is a constant proportional to the product of the gravitational constant G and the masses m and M of the interacting bodies, and K_2 is a constant with dimensions of length. For large values of K_2, the Yukawa potential approximates Newtonian gravity, as K_2 \to \infty leads to the familiar 1/R dependence. The Yukawa potential can give rise to bounded orbits (circular and elliptical) when K_2 is sufficiently large.
This potential introduces a correction to the Newtonian law, incorporating an exponential decay term. This article explores the interaction between two celestial bodies, specifically the Sun and Earth, under this modified potential. We will examine how this potential affects key orbital parameters such as the aphelion and eccentricity, providing a comparative analysis with the classical Newtonian model.
Sun / Earth simulation
Let’s consider a 2 body problem, so that there is an exact solution, with the Earth orbiting around the Sun, and assuming that, with the modified potential, the energy and the angular momentum are not changed.
Considering the two bodies, with the following parameters:
\begin{aligned} & M_{\text{Sun}} = M_{\odot} = 1.989 \times 10^{30} \text{ kg}\\ & M_{\text{Earth}} = M_{\oplus} = 5.972 \times 10^{24} \text{ kg}\\ & G = 6.67430 \times 10^{-11} \, \frac{\text{m}^3}{\text{kg} \cdot \text{s}^2}\\ & r_p = 1.47100396 \times 10^{11} \text{ m}\\ & r_a = 1.51854870 \times 10^{11} \text{ m}\\ & K_2 = 2 \times 10^{15} \text{ m} \end{aligned}
the radius for the aphelion and the perihelion has been computed numerically. The energy and the angular momentum is:
\begin{aligned} & E = -\frac{G M_{\odot} M_{\oplus}}{r_a + r_p} = -2.65188 \times 10^{33} \, \text{J} \\ & L = M_{\oplus} \sqrt{\frac{G M_{\odot} (2 r_p r_a)}{r_p + r_a}} = 2.65995 \times 10^{40} \, \text{kg} \cdot \text{m}^2 \cdot \text{s}^{-1} \end{aligned}
Computing the kinetic and potential energy at apoapsis (r_a):
\begin{aligned} & T_{r_a} = \frac{L^2}{2 M_{\oplus} r_a^2} = 2.73759 \times 10^{33} \, \text{J}\\ & U_{r_a} = -\frac{G M_{\odot} M_{\oplus}}{r_a} = -5.38948 \times 10^{33} \, \text{J}\\ & E_{r_a} = T_{r_a} + U_{r_a} = -2.65188 \times 10^{33} \, \text{J} = E \end{aligned}
Computing the kinetic and potential energy at periapsis (r_p):
\begin{aligned} & T_{r_p} = \frac{L^2}{2 M_{\oplus} r_p^2} = 2.56885 \times 10^{33} \, \text{J} \\ & U_{r_p} = -\frac{G M_{\odot} M_{\oplus}}{r_p} = -5.22073 \times 10^{33} \, \text{J}\\ & E_{r_p} = T_{r_p} + U_{r_p} = -2.65188 \times 10^{33} \, \text{J} = E \end{aligned}
New aphelion and perihelion
In order to compute the modified aphelion and the perihelion it is possible to use the assumption that the energy and the angular momentum are constant and therefore:
\begin{aligned} & E = T + U = const \\ & T_{r_a^{'}} + U_{r^{'}} = \frac{L^2}{2 M_{\oplus} {r^{'}}^2} -\frac{G M_{\odot} M_{\oplus}}{r^{'}}e^{-\frac{r^{'}}{K_1}} = E \end{aligned}
This function is parabolic and there are two zeros.
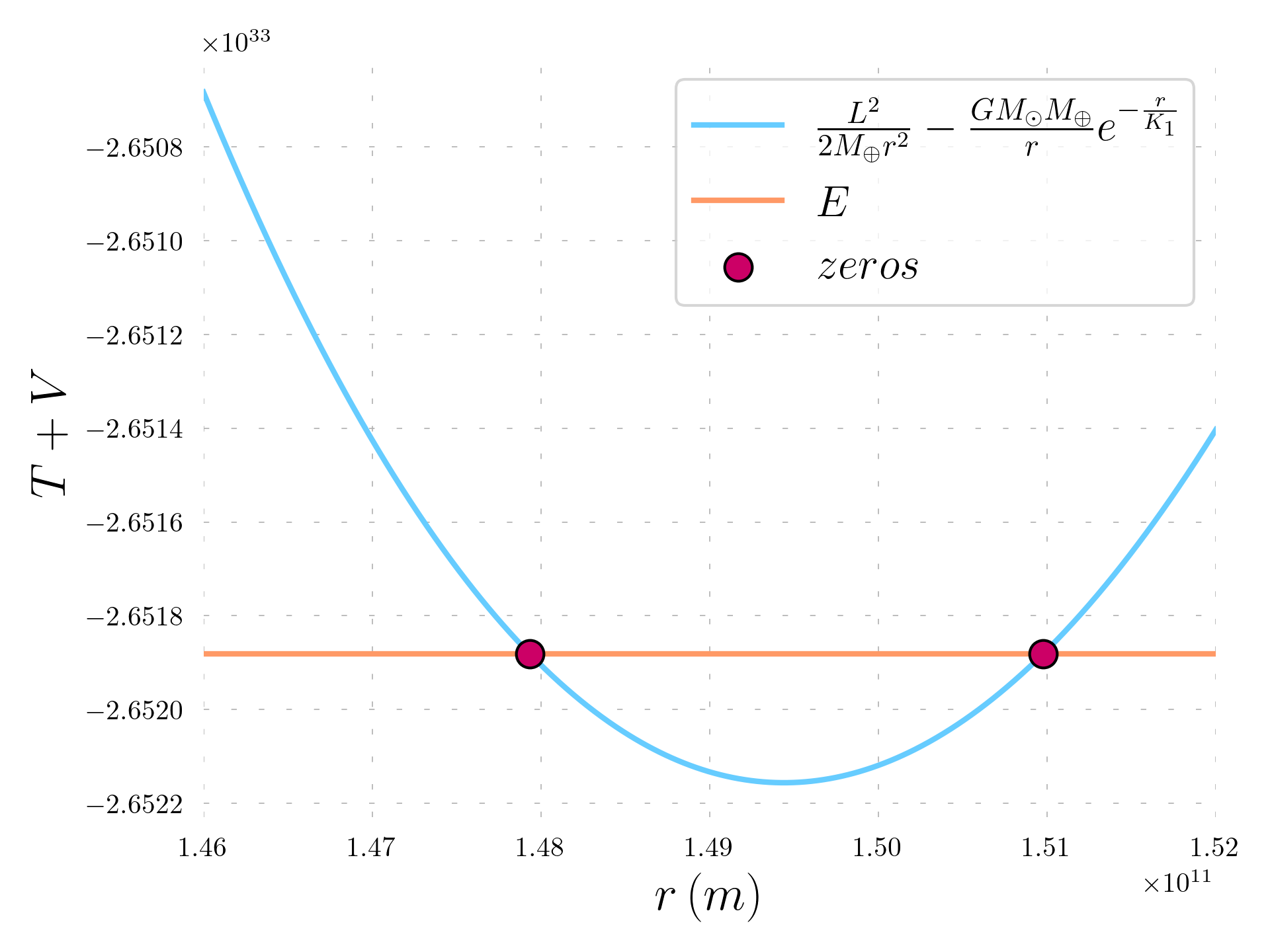
The zeros can be computed using Python and taking as initial guesses the Newtonian aphelion and perihelion.
import numpy as np
from scipy.optimize import fsolve
# Constants
M_sun = 1.989e30 # kg
M_earth = 5.972e24 # kg
G = 6.67430e-11 # m^3 kg^-1 s^-2
r_p = 1.47100396e+11 # m
r_a = 1.51854870e+11 # m
K1 = 2e15 # m
E = -G * M_sun * M_earth / (r_a + r_p)
L = M_earth * np.sqrt(G * M_sun * (r_a + r_p) / 2 * (
1 - ((r_a - r_p)**2 / (r_a + r_p)**2)))
def f(r):
# Function to calculate the left side of the equation
term1 = L**2 / (2 * M_earth * r**2)
term2 = G * M_sun * M_earth / r * np.exp(-r / K1)
return term1 - term2
def func_to_solve(r):
# Function to find zeros
return f(r) - E
# Range of r
r = np.linspace(1.46e11, 1.52e11, 1000) # m
# Calculate the function values
f_values = f(r)
# Initial guesses for the zeros
initial_guesses = [1.47100396e11, 1.51854870e11]
# Finding the zeros
zeros = fsolve(func_to_solve, initial_guesses)
print(zeros)
The results are:
\begin{aligned} & r_p^{'} = 1.4793488 \times 10^{11} \text{ m}\\ & r_a^{'} = 1.5097571 \times 10^{11} \text{ m}\\ \end{aligned}
Eccentricity
Newton’s law yields elliptical orbits. If the Sun is located at the origin, the radius r of an orbit as a function of the angle \theta from the Sun is given by:
r = \frac{b}{1 + e \cos(\theta)}
where e is the eccentricity of the orbit, and b is a constant with units of length. For elliptical orbits, 0 < e < 1.
For the Yukawa potential, if K_2 is large enough, the orbits are nearly elliptical, and a similar formula holds with only the eccentricity modified:
r = \frac{b}{1 + e^{'} \cos(\theta)}
where e^{'} is the modified eccentricity. We know with the radius at two points: r_p (the perihelion, the closest point) and r_a (the aphelion, the farthest point). At the perihelion, \theta = 0, and at the aphelion, \theta = \pi.
At the perihelion (\theta = 0), we have:
r_p = \frac{b}{1 + e}
At the aphelion (\theta = \pi), we have:
r_a = \frac{b}{1 - e}
Now, we can solve these two equations for b and e.
From the perihelion equation:
b = r_p (1 + e)
From the aphelion equation:
b = r_a (1 - e)
Equating the two expressions for b:
r_p (1 + e) = r_a (1 - e)
Expanding and rearranging to solve for e:
\begin{aligned} & r_p + r_p e = r_a - r_a e \\ & r_p e + r_a e = r_a - r_p \\ & e(r_p + r_a) = r_a - r_p \\ & e = \frac{r_a - r_p}{r_a + r_p} \end{aligned}
Using the perihelion equation with the expression for e:
b = r_p \left(1 + \frac{r_a - r_p}{r_a + r_p}\right)
Simplify the expression:
b = r_p \left(\frac{r_a + r_p + r_a - r_p}{r_a + r_p}\right) = r_p \left(\frac{2r_a}{r_a + r_p}\right) = \frac{2r_a r_p}{r_a + r_p}
The final expressions are:
\begin{aligned} & e = \frac{r_a - r_p}{r_a + r_p} \\ & b = \frac{2r_a r_p}{r_a + r_p} \end{aligned}
With the values previously computed we got for Newton potential:
\begin{aligned} & e = 1.5904\times 10^{-2} \\ & b = 1.4944 \times 10^{11} \text{ m} \end{aligned}
And for the Yukawa potential:
\begin{aligned} & e^{'} = 1.0173 \times 10^{-2} \\ & b^{'} = 1.4944 \times 10^{11} \text{ m} \end{aligned}
The difference is:
\begin{aligned} & \delta e = e^{'} - e = -5.7306 \times 10^{-2} \\ & \delta b = b^{'} - b = 4.1719 \times 10^{2} \text{ m} \end{aligned}
It is possible to compute this difference in an analytical form. Starting from the energy definition:
E = -\frac{G M_{\odot} M_{\oplus}}{r_a + r_p}
and using the fact that:
r_p + r_a = \frac{b}{1 + e} + \frac{b}{1 - e} = \frac{2b}{1-e^2}
Then:
E = -\frac{G M_{\odot} M_{\oplus}}{r_a + r_p} = -\frac{G M_{\odot} M_{\oplus}\left(1-e^2\right)}{2b}
We can retrieve the eccentricity as function of e=e(E,b):
e = \sqrt{1 + \frac{2bE}{G M_{\odot} M_{\oplus}}}
then:
e^2 = 1 + \frac{2bE}{G M_{\odot} M_{\oplus}}
Let’s consider the Yukawa potential and Taylor expand the exponential for the potential energy
E^{'} = T + U = T -\frac{G M_{\odot} M_{\oplus}}{r^{'}}e^{-\frac{r^{'}}{K_1}} = T -\frac{G M_{\odot} M_{\oplus}}{r^{'}} \left(1 -\frac{r^{'}}{K_1}\right)
So it can be written as:
E^{'} = E - \frac{G M_{\odot} M_{\oplus}}{K_1}
This energy correction is in percentage:
\Delta E\% = \frac{\left|\frac{G M_{\odot} M_{\oplus}}{K_1}\right|}{E}*100 = 0.01495\%
As K_2 is large, the constant shift found in the previous step is small and we assume that the relation between the eccentricity and energy for the Newtonian case also applies to the Yukawa case, but just replacing e with e^{′} and E with E^{′}:
e^{'} = \sqrt{1 + \frac{2bE^{'}}{G M_{\odot} M_{\oplus}}}
We can then use the relationship previously derived:
e^{'} = \sqrt{1 + \frac{2bE^{'}}{G M_{\odot} M_{\oplus}}} = \sqrt{1 + \frac{2bE}{G M_{\odot} M_{\oplus}} - \frac{2b}{K_2}}
Using the expression of e^2:
e^{'} = \sqrt{1 + \frac{2bE}{G M_{\odot} M_{\oplus}} - \frac{2b}{K_2}} = \sqrt{e^2 - \frac{2b}{K_2}} = e\sqrt{1 - \frac{2b}{e^2 K_2}}
Taylor expanding this expression using (1+x)^y \approx 1+yx:
e^{'} = e\sqrt{1 - \frac{2b}{e^2 K_2}} = e\left(1 - \frac{1}{2}\frac{2b}{e^2 K_2}\right) = e - \frac{b}{e K_2}
That gives an approximation of \delta e:
\delta e_1 = e^{'} - e = -\frac{b}{eK_2}
Using the previously computed data:
\delta e_1 = e^{'} - e = -\frac{b}{eK_2} = -4.6983 \times 10^{-2}
Compared to the previously calculated values, the percentage error is:
\Delta(\delta e)\% = \left|\frac{\delta e - \delta e_1}{\delta e}\right|*100 \approx 18\%
So the first order estimate is introducing and error of ~20\%. Using the expression:
e^{'} = e\sqrt{1 - \frac{2b}{e^2 K_2}} \approx 1.0173 \times 10^{-2}
Gives a much better estimate:
\delta e_2 = e\left(\sqrt{1 - \frac{2b}{e^2 K_2}} - 1\right) = -5.7308 \times 10^{-3}
Compared to the previously calculated values, the percentage error is:
\Delta(\delta e)\% = \left|\frac{\delta e - \delta e_2}{\delta e}\right|*100 = 4.7894 \times 10^{-3} \%
The difference is now only 0.0048\%.