Solutions

Exercise list

Lecture 5

Exercise 5.1

Exercise 5.2

Exercise 5.3

Lecture 6

Exercise 6.1

Exercise 6.2

Exercise 6.3

Exercise 6.4

Exercise 6.5

Exercise 6.6

Lecture 7

Exercise 7.1

Exercise 7.2

Exercise 7.3

Exercise 7.4

Exercise 7.5

Exercise 7.6

Exercise 7.7

Lecture 5

Exercise 5.1

The formula can be proven in two ways, starting from the exercise request and using the product rule:

\frac{\mathrm d v^2}{\mathrm dt} = \frac{\mathrm d}{\mathrm dt}\left(v\cdot v\right) = \frac{\mathrm dv}{\mathrm dt} v + v \frac{\mathrm dv}{\mathrm dt} = 2v \frac{\mathrm dv}{\mathrm dt} = 2v \, \dot v

That can also be proven faster using the chain rule:

\frac{\mathrm d v^2}{\mathrm dt} = \frac{\mathrm d v}{\mathrm dt}\mathrm d\left(v^2\right) = 2v \frac{\mathrm d v}{\mathrm dt} = 2v\,\dot v

Exercise 5.2

The exercise has been analyzed in details in a specific page here.

Exercise 5.3

Starting from the potential:

V = \frac{k}{2\left( x^2 + y^2 \right)}

and applying Newton’s equations:

\begin{aligned} \frac{dV}{dx} &= -\frac{kx}{(x^2 + y^2)^2} \\ \frac{dV}{dy} &= -\frac{ky}{(x^2 + y^2)^2} \\ m\ddot{x} &= \frac{kx}{m(x^2 + y^2)^2} \\ m\ddot{y} &= \frac{ky}{m(x^2 + y^2)^2} \end{aligned}

That gives the equations of motion. This potential can be also express in polar coordinates as:

V(r) = \frac{k}{2r^2}

In a central force field, circular orbits occur when the centrifugal force precisely balances the central force. This balance is encapsulated in the concept of the effective potential V_e, which combines the actual potential with the centrifugal term, and can be be seen precisely in polar coordinates (r, \theta).

The effective potential in polar coordinates is given by:

V_e(r) = V(r) + \frac{L^2}{2mr^2}

where L is the conserved angular momentum in a central force field. For the given potential, substituting this into the effective potential yields:

V_e(r) = \frac{k}{2r^2} + \frac{L^2}{2mr^2} = \frac{k + \frac{L^2}{m}}{2r^2}

To find the conditions for circular orbits, we look for the minimum of the effective potential, where \frac{\mathrm dV_e}{\mathrm dr} = 0. This condition signifies a balance of forces, characteristic of a circular orbit. Calculating the derivative gives:

\frac{\mathrm dVe}{\mathrm dr} = -\frac{k+\frac{L^2}{m}}{r^3}

Setting this derivative to zero should reveal the radius r = r_0 at which the effective force vanishes, indicating a potential circular orbit. However, given that both k and \frac{L^2}{m} are positive, this equation implies there are no finite values of r for which the effective force is zero. This absence of a zero-crossing in the derivative of the effective potential suggests that circular orbits are not feasible under this potential energy configuration.

In conclusion, the specific potential energy V = \frac{k}{2\left( x^2 + y^2 \right)} does not support circular orbits. The precise nature of the orbits would require analysis employing numerical methods.

To demonstrate that the energy for the motion described by the potential V = \frac{k}{2(x^2 + y^2)} is conserved, we can show that \frac{\mathrm dE}{\mathrm dt} = 0, where E is the total energy of the system.

The total energy E is the sum of kinetic energy T and potential energy V:

E = T + V

For a particle of mass m moving in two dimensions, the kinetic energy is given by:

T = \frac{1}{2}m(\dot{x}^2 + \dot{y}^2)

And the potential energy V is given by:

V = \frac{k}{2(x^2 + y^2)}

Therefore, the total energy E is:

E = \frac{1}{2}m(\dot{x}^2 + \dot{y}^2) + \frac{k}{2(x^2 + y^2)}

To show that \frac{\mathrm dE}{\mathrm dt} = 0, we differentiate E with respect to time:

\frac{\mathrm dE}{\mathrm dt} = m(\dot{x}\ddot{x} + \dot{y}\ddot{y}) - \frac{k(x\dot{x} + y\dot{y})}{(x^2 + y^2)^2}

Using the equations of motion derived from the Newton's equations, where \ddot{x} = \frac{kx}{m(x^2 + y^2)^2} and \ddot{y} = \frac{ky}{m(x^2 + y^2)^2}, we substitute these into the expression for \frac{dE}{dt}:

\frac{dE}{dt} = \frac{kx\dot{x}}{(x^2 + y^2)^2} + \frac{ky\dot{y}}{(x^2 + y^2)^2} - \frac{k(x\dot{x} + y\dot{y})}{(x^2 + y^2)^2} = 0

This demonstrates that \frac{dE}{dt} = 0, hence the energy for this motion is conserved.

Exercise 6.1

Considering a system composed by one particle, with a potential energy V(x) and a kinetic energy T = \frac{m\,\dot x^2}{2}, the Lagrangian is:

\mathcal L = T - V = \frac{m\,\dot x^2}{2} - V(x)

Applying the Euler-Lagrangian equations:

\begin {aligned} & \dfrac{\mathrm d}{\mathrm dt} \left( \dfrac{\partial \mathcal L}{\partial \dot x} \right) = \dfrac{\mathrm d}{\mathrm dt} \left(- 2 \frac{m \, \dot x}{2} \right) = m\, \ddot x \\ & \dfrac{\partial \mathcal L}{\partial x} = - \dfrac{\mathrm dV(x)}{\mathrm dx} \\[5pt] & m\, \ddot x= - \dfrac{\mathrm dV(x)}{\mathrm dx} = F(x) \end{aligned} This gives the Newton equations for the particle.

Exercise 6.2

This is a generalization of the previous exercise. Considering a system with multiple particles, with a potential energy V(x_i) and a kinetic energy T = \frac{m\,\dot x_i^2}{2} the Lagrangian for this systems composite system is:

\mathcal L_i = T_i - V_ = \frac{m\,\dot x_i^2}{2} - V(x_i)

Applying the Euler-Lagrangian equations:

\begin {aligned} & \dfrac{\mathrm d}{\mathrm dt} \left( \dfrac{\partial \mathcal L_i}{\partial \dot x_i} \right) = \dfrac{\mathrm d}{\mathrm dt} \left(- 2 \frac{m \, \dot x_i}{2} \right) = m\, \ddot x_i \\ & \dfrac{\partial \mathcal L_i}{\partial x_i} = - \dfrac{\mathrm dV(x_i)}{\mathrm dx_i} \\[5pt] & m\, \ddot x_i = - \dfrac{\mathrm dV(x_i)}{\mathrm dx_i} = F(x_i) \end{aligned} In this case also it gives the Newton’s equations.

Exercise 6.3

Exercise 6.3

There are two reasons to use the principle of least action and therefore the Lagrangian formulation:

• it packages everything about a system in a single equation;
• there are practical advantages and the equations could be simpler than Newton’s equations.

It is complex to rewrite the Newton’s equations in a different set of coordinates (or if the reference frame is moving or accelerating), but it is sufficient to write the Lagrangian and then the equations of motions are derived from it; the principle of least action is not dependent from the coordinate used.

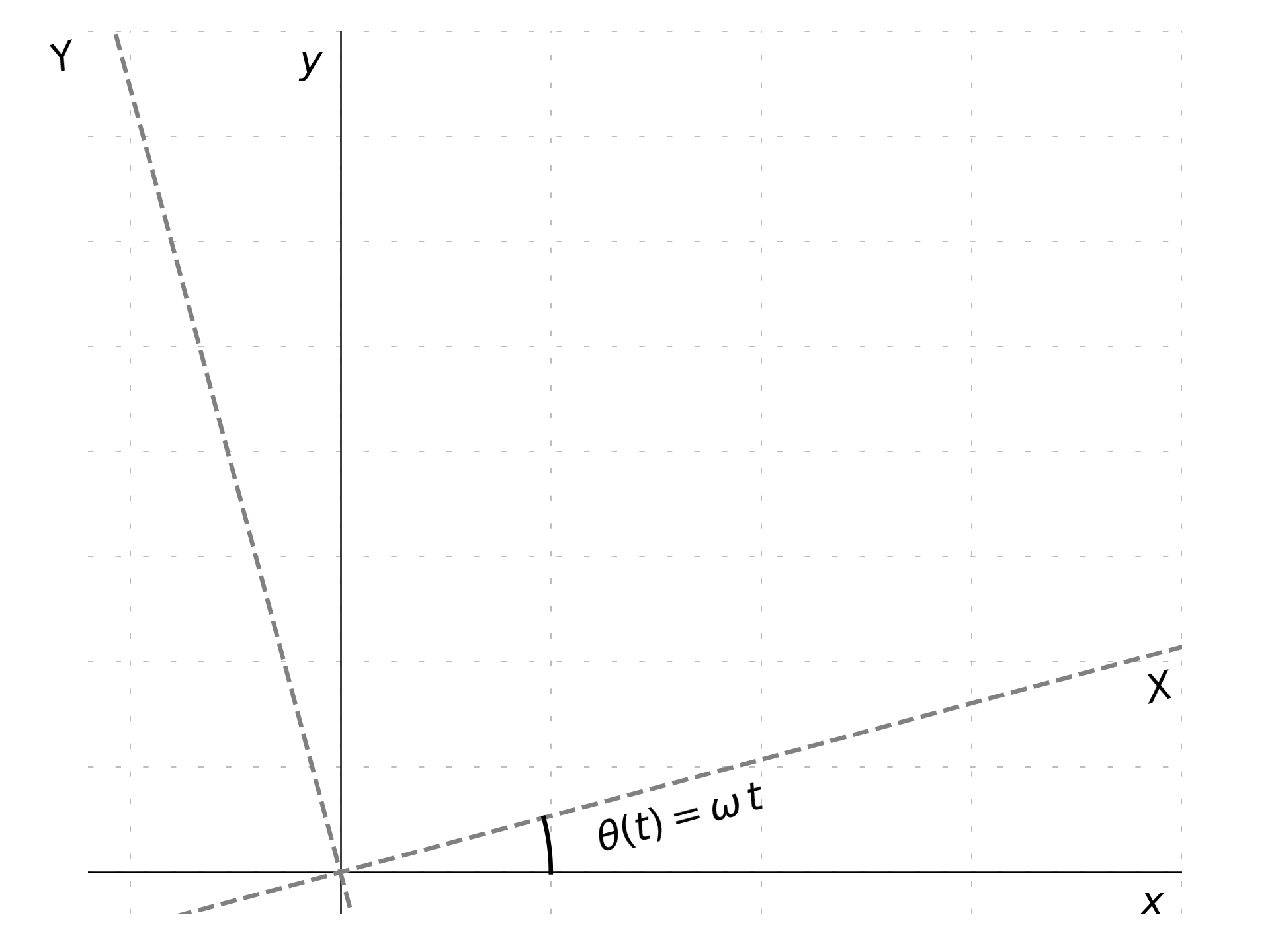
As example, it is possible to consider two frames of reference:

• an inertial frame of reference x,y;
• a rotating frame of reference X,Y with a velocity \theta(t) = \omega\,t (as if an observer is standing on a carousel).

There are no force applied to this system F = m\,\ddot x = 0. The transformation between the two coordinates is:

\begin{array}{c} x = X\,\cos(\omega\,t) + Y\,\sin(\omega\,t) \\ y = - X\,\sin(\omega\,t) + Y\,\cos(\omega\,t) \end{array}

In the reference inertial frame, the Lagrangian is (there is no potential energy):

\mathcal L = \frac{m}{2}\left(\dot x^2 + \dot y^2\right)

and applying the Euler-Lagrange equations gives:

m\,\ddot x = 0 \quad m\,\ddot y = 0

It is simple to now change the coordinates, and it is just necessary to differentiate the coordinate transformation and put into the Lagrangian:

\begin{array}{c} \dot x = \dot X\,\cos(\omega\,t) - X\,\omega\,\sin(\omega\,t) + \dot Y\,\sin(\omega\,t) + Y\,\omega\,\cos(\omega\,t) \\ \dot y = - \dot X\,\sin(\omega\,t) - X\,\omega\,\cos(\omega\,t) + \dot Y\,\cos(\omega\,t) - Y \,\omega\,\sin(\omega\,t) \end{array}

Now it is possible to substitute:

\begin{aligned} \mathcal L = & \frac{m}{2}\left(\dot x^2 + \dot y^2\right) \\ = & \frac{m}{2}\left[ \left(\dot X\,\cos(\omega\,t) - X\,\omega\,\sin(\omega\,t) + \dot Y\,\sin(\omega\,t) + Y\,\omega\,\cos(\omega\,t) \right)^2 \right. \\ & \left. + \left(- \dot X\,\sin(\omega\,t) - X\,\omega\,\cos(\omega\,t) + \dot Y\,\cos(\omega\,t) - Y \,\omega\,\sin(\omega\,t) \right)^2\right] \\ = & \frac{m}{2}\left[ \dot X^2 + \dot Y^2 + \omega^2 \left(X^2 + Y^2\right) + 2 \omega \left(\dot X \, Y - X \dot Y \right) \right] \end{aligned}

Before applying the Euler-Lagrangian equation, it is possible to analyze this formulation:

• if the coordinates are not rotating (\omega = 0) then the Lagrangian is exactly the same as the inertial reference;
• the second term seems a fictitious potential energy V = -\frac{m}{2}\omega^2(X^2+Y^2) from the origin and pointing outwards. This is the centrifugal force;
• the last term \frac{m}{2}\omega (\dot X \, Y - X \dot Y) is the Coriolis force, which depend both on coordinates and velocities at the same time.

It is now possible to write the Euler-Lagrangian equations:

\begin{aligned} & \frac{\mathrm d}{\mathrm dt}\left( \dfrac{\partial \mathcal L}{\partial \dot X} \right) = \frac{\mathrm d}{\mathrm dt}\left( \dfrac{2\,m\,\dot X}{2} + \dfrac{2\,m\,\omega\,Y}{2} \right) = m\, \ddot X + m\,\omega \dot Y \\ & \dfrac{\partial \mathcal L}{\partial X} = \dfrac{m}{2}\left( \omega^2 2 X - 2\,\omega Y \right) = m\,\omega^2 X - m\,\omega \dot Y \\ & \frac{\mathrm d}{\mathrm dt}\left( \dfrac{\partial \mathcal L}{\partial \dot Y} \right) = \frac{\mathrm d}{\mathrm dt}\left( \dfrac{2\,m\,\dot Y}{2} - \dfrac{2\,m\,\omega\,X}{2} \right) = m\, \ddot Y - m\,\omega \dot X \\ & \dfrac{\partial \mathcal L}{\partial Y} = \dfrac{m}{2}\left( \omega^2 2 Y + 2\,\omega X \right) = m\,\omega^2 Y + m\,\omega \dot X \end{aligned}

Equating the terms gives the equations of motions:

\begin{aligned} & m\, \ddot X = m\,\omega^2 X -2\,m\,\omega \dot Y \\ & m\, \ddot Y = m\,\omega^2 Y +2\,m\,\omega \dot X \end{aligned}

An interesting observation can be done for the Coriolis force:

\begin{aligned} & F_x = -2\,m\,\omega \dot Y \\ & F_y = 2\,m\,\omega \dot X \end{aligned}

This force is always perpendicular to the velocity and proportional to the magnitude of it as:

\mathbf v \cdot \mathbf F = \dot X \, F_x + \dot Y \, F_y = -\dot X 2\, m\,\omega \dot Y + \dot Y 2\,m\,\omega \dot X = 0

It is also possible to prove that circular motion is a solution of these equations. A circular motion has the form:

\begin{aligned} X(t) &= A \cos(\omega t + \phi) \\ Y(t) &= A \sin(\omega t + \phi) \end{aligned}

Taking the derivatives of X(t) and Y(t) with respect to time:

\begin{aligned} & \dot{X}(t) = -A \, \omega \, \sin(\omega t + \phi) \\ & \ddot{X}(t) = -A \, \omega^2 \cos(\omega t + \phi) \\ & \dot{Y}(t) = A \, \omega \, \cos(\omega t + \phi) \\ & \ddot{Y}(t) = -A \, \omega^2 \sin(\omega t + \phi) \end{aligned}

Substituting in the original equations:

\begin{aligned} & m\, \ddot X = m\,\omega^2 X -2\,m\,\omega \dot Y \\ & -m\,A \, \omega^2 \,\cos(\omega t + \phi) = m\,\omega^2 \,A \,\cos(\omega t + \phi) - 2\,m\,\omega\, A\,\omega \, \cos(\omega t + \phi) \\ & m\, \ddot Y = m\,\omega^2 Y +2\,m\,\omega \dot X \\ & -m\, A \, \omega^2 \sin(\omega t + \phi) = m\,\omega^2 \, A \sin(\omega t + \phi) - 2\,m\,\omega \, A \, \omega\, \sin(\omega t + \phi) \end{aligned}

These equations are always satisfied.

Exercise 6.4

Similar to the previons exercise, this time using polar coordinates:

\begin{aligned} x & = R\cos(\theta) \\ y & = R\sin(\theta) \end{aligned}

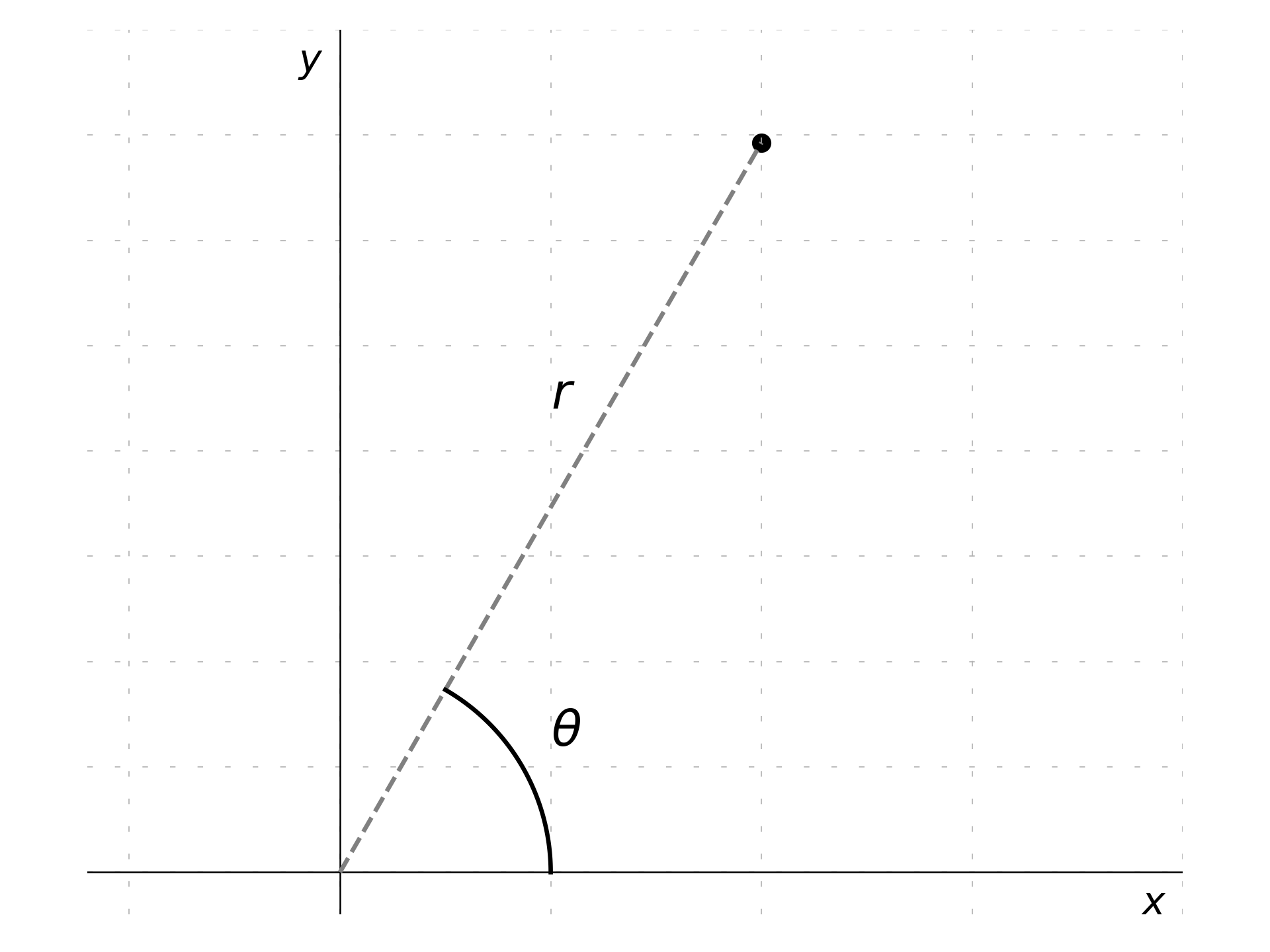
The process is similar:

\begin{aligned} \dot x & = \dot r \cos(\theta) - r \sin(\theta)\dot \theta \\ \dot y & = \dot r \sin(\theta) + r \cos(\theta)\dot \theta \end{aligned}

Then substituting:

\begin{aligned} \mathcal L = & \frac{m}{2}\left(\dot x^2 + \dot y^2\right) = \left[ \left(\dot r \cos(\theta) - r \sin(\theta)\dot \theta \right)^2 + \left(\dot r \sin(\theta) + r \cos(\theta)\dot \theta \right)^2\right] \\ = & \frac{m}{2}\left(\dot r^2 + r^2\, \dot \theta^2\right) \end{aligned}

Eventually it is possible to add a potential energy (for example V= V(r)):

\mathcal L = \frac{m}{2}\left(\dot r^2 + r^2\, \dot \theta^2\right) - V(r)

Now is it possible to write the Euler-Lagrange equations for r and \theta:

\begin{aligned} & \frac{\mathrm d}{\mathrm dt}\left( \dfrac{\partial \mathcal L}{\partial \dot r} \right) = m\,\ddot r \\ & \dfrac{\partial \mathcal L}{\partial r} = m\,r\,\dot\theta^2-\dfrac{\mathrm dV}{\mathrm dr} \\ & \frac{\mathrm d}{\mathrm dt}\left( \dfrac{\partial \mathcal L}{\partial \dot \theta} \right) = \frac{\mathrm d}{\mathrm dt}\left(m\, r^2 \dot \theta \right)\\ & \dfrac{\partial \mathcal L}{\partial \theta} = 0 \end{aligned}

Equating the terms gives the equations of motions:

\begin{aligned} & m\,\ddot r = m\,r\,\dot\theta^2-\dfrac{\mathrm dV}{\mathrm dr} \\ & \dfrac{\mathrm d}{\mathrm dt}\left(m\, r^2 \dot \theta \right) = 0 \end{aligned}

The second equation tell that r^2 \dot \theta is conserved; This is the conservation of angular momentum and derives from the fact the V is only a function of r but does not depends on \theta. If a Lagrangian does not depends explicitly from a coordinate (\theta in this case) it is called cyclical coordinate and there is associated a conservation law, as there is not RHS.

The angular momentum is depending from the initial conditions but it is a constant:

m\, r^2 \, \dot \theta = L

computing \dot \theta and substituting it gives an equation for r

\ddot r = \frac{L}{m^2\,r^3} - \frac{1}{m} \dfrac{\mathrm dV}{\mathrm dr}

Exercise 6.5

The exercise has been analyzed in details in a specific page here.

Exercise 6.6

Considering two particles of the same mass moving on a line with a potential energy that depends on the distance between them; the Lagrangian is:

\mathcal L = T - V = \frac{m\,\dot x^2}{2} - V(x) = \frac{m}{2}\left(\dot x_1^2 + \dot x_2^2 \right) - V\left(x_1 - x_2\right)

Changing the coordinates:

\begin{aligned} x_{+} & = \frac{x_1 + x_2}{2} \\ x_{-} & = \frac{x_1 - x_2}{2} \end{aligned}

The Lagrangian can be rewritten, retrieving x_1 and x_2:

\begin{aligned} x_{1} & = x_{+} + x_{-} \\ x_{2} & = x_{+} - x_{-} \end{aligned}

and deriving:

\begin{aligned} \dot x_{1} & = \dot x_{+} + \dot x_{-} \\ \dot x_{2} & = \dot x_{+} - \dot x_{-} \end{aligned}

So that the kinetic energy is now:

\begin{aligned} T & = \frac{m}{2}\left(\dot x_1^2 + \dot x_2^2 \right) = \frac{m}{2}\left[\left(\dot x_{+} + \dot x_{-}\right)^2 + \left(\dot x_{+} - \dot x_{-}\right)^2 \right] \\ & = \frac{m}{2}\left[\left(\dot x_{+}^2 + 2 \dot x_{+}\dot x_{-} + \dot x_{-}\right) + \left(\dot x_{+}^2 - 2\dot x_{+}\dot x_{-} + \dot x_{-}^2\right) \right] \\ & = \frac{m}{2}\left(2\dot x_{+}^2 + 2\dot x_{-}^2 \right) = m\left(\dot x_{+}^2 + \dot x_{-}^2 \right) \end{aligned}

The Lagrangian become:

\mathcal L = m\left(\dot x_{+}^2 + \dot x_{-}^2 \right) - V\left(2 x_{-}\right)

with the conjugate momentum to x_{+} (a cyclic coordinate that does not appears in the Lagrangian) which is conserved.

Exercise 7.1

considering the Lagrangian (the same as the exercise 6.6):

\mathcal L = \frac{\dot q_1^2 + \dot q_2^2}{2} - V\left(q_1 - q_2 \right)

This can interpreted as two particles of unitary mass sitting on a line where the potential depends only from the distance between these two particles.

It is possible to write the equation of motion:

\begin {aligned} & \dfrac{\mathrm d}{\mathrm dt} \left( \dfrac{\partial \mathcal L}{\partial \dot q_1} \right) = \dfrac{\mathrm d}{\mathrm dt} \left(- 2 \frac{\dot q_1}{2} \right) = \ddot q_1 \equiv \dot p_1 \\ & \dfrac{\partial \mathcal L}{\partial q_1} = - \dfrac{\mathrm d}{\mathrm dq_1}\left(q_1 - q_2\right) = V'\left(q_1 - q_2\right) \\[5pt] & \dfrac{\mathrm d}{\mathrm dt} \left( \dfrac{\partial \mathcal L}{\partial \dot q_2} \right) = \dfrac{\mathrm d}{\mathrm dt} \left(- 2 \frac{\dot q_2}{2} \right) = \ddot q_2 \equiv \dot p_2 \\ & \dfrac{\partial \mathcal L}{\partial q_2} = - \dfrac{\mathrm d}{\mathrm dq_1}V\left(q_1 - q_2\right)(-1) = +V'\left(q_1 - q_2\right) \end{aligned}

Putting all together:

\begin{aligned} & \ddot q_1 = \dot p_1 = - V'\left(q_1 - q_2\right) \\ & \ddot q_2 = \dot p_2 = V'\left(q_1 - q_2\right) \\ \end{aligned}

In these equation it was used the definition of the momentum conjugated with q_i, and V' is by convention the derivative of the potential energy evaluated in a point. The sign of the second equations comes from apply the chain rule (\frac{\mathrm d}{\mathrm dq_2}\left(q_1 - q_2\right) = -1).

Summing these two equations gives:

\frac{\mathrm d}{\mathrm dt} \left(p_1 + p_2 \right) = 0

This imply the conservation of total momentum and there is a conservation law.

Exercise 7.2

For a more generic potential of the form:

V(q_1, q_2) = V\left(a\,q_1 - b\, q_2\right)

A similar derivation as the one in Exercise 7.1 leads to:

\begin{aligned} & \ddot q_1 = \dot p_1 = -a \, V'\left(a\,q_1 - b\, q_2\right) \\ & \ddot q_2 = \dot p_2 = +b \, V'\left(a\,q_1 - b\, q_2\right) \\ \end{aligned}

so now the sum of p_1 + p_2 is no longer conserved, but multiplying the first equation for b, the second for a and summing:

\frac{\mathrm d}{\mathrm dt} \left(b\,p_1 + a\,p_2\right) = 0

So the quantity b\,p_1 + a\,p_2 is conserved; this can be interpreted as a generalized momentum corresponding to the symmetry of the potential under translations in a specific direction in the p_1\,p_2-plane. The direction is determined by the coefficients a and b, and the conservation law implies that the motion of the system in this direction is such that the weighted sum of p_1 and p_2, with weights a and b, remains constant over time.

The correspondent Lagrangian is:

\mathcal L = \frac{\dot q_1^2 + \dot q_2^2}{2} - V\left(a\,q_1 - b\, q_2\right)

This formulation has a practical implementation. Suppose there are two particle of mass m_1 and m_2 and x_1 and x_2 are the position along the line which goes through their center, and the potential force is proportional to the distance; the Lagrangian is:

\mathcal L = \frac{m_1 \dot x_1^2}{2} + \frac {m_2 \dot x_2^2}{2} + V(x_1 - x_2)

Applying the transformation:

\begin{aligned} & q_1 = \sqrt {m_1}\, x_1 \\ & q_2 = -\sqrt {m_2}\, x_2 \end{aligned}

it becomes:

\begin{aligned} & m_1 \dot x_1^2 = \dot q_1^2, \quad x_1 = \dfrac{q_1}{\sqrt{m_1}} \\ & m_2 \dot x_2^2 = \dot q_2^2, \quad x_2 = -\dfrac{q_2}{\sqrt{m_2}} \end{aligned}

The Lagrangian takes the form:

\mathcal L = \frac{\dot q_1^2}{2} + \frac {\dot q_2^2}{2} + V\left(\dfrac{q_1}{\sqrt{m_1}} + \dfrac{q_2}{\sqrt{m_2}}\right)

with a potential energy of the form V(a\,q_1 + b\,q_2). Originally, the kinetic energy had few terms and the potential energy a simple formulation, while in this second case after the transformation is the opposite, and this is a general pattern: it is possible to transform the coordinates and simplify either the formulation of the kinetic or potential energy, but not both.

Exercise 7.3

Starting from the Lagrangian:

\mathcal L = \frac{\dot q_1^2 + \dot q_2^2}{2} - V\left(a\,q_1 - b\, q_2\right)

Considering the transformation (using the more common \varepsilon for a small increment in place of the \delta used in the book):

\begin{aligned} & q_1' = q_1 + b\,\varepsilon \\ & q_2' = q_2 - a\,\varepsilon \end{aligned}

Since \varepsilon is constant, the derivatives of these are not changing:

\begin{aligned} & \dot q_1' = \frac{\mathrm d}{\mathrm dt}\left(q_1 + b\,\varepsilon \right) = \dot q_1 \\ & \dot q_1' = \frac{\mathrm d}{\mathrm dt}\left(q_1 + b\,\varepsilon \right) = \dot q_1 \end{aligned}

There is no change in the potential energy as it does not change with this transformation:

V(a\,q_1' + b\,q_2') = V(a\,q_1 + a\,b\,\varepsilon + b\,q_2 -a\,\,b\, \varepsilon) = V(a\,q_1 + b\, q_2)

Therefore, is a symmetry and a conservation law and the Lagrangian is not changed:

\mathcal L = \frac{\dot q_1'^2 + \dot q_2'^2}{2} - V\left(a\,q_1' - b\, q_2'\right) = \frac{\dot q_1^2 + \dot q_2^2}{2} - V\left(a\,q_1 - b\, q_2\right)

Exercise 7.4

Let’s consider a single particle moving in a two dimensional Cartesian coordinates system (then x,y will be used in place of q_1,q_2, with the potential energy which depends only on the distance from the origin.

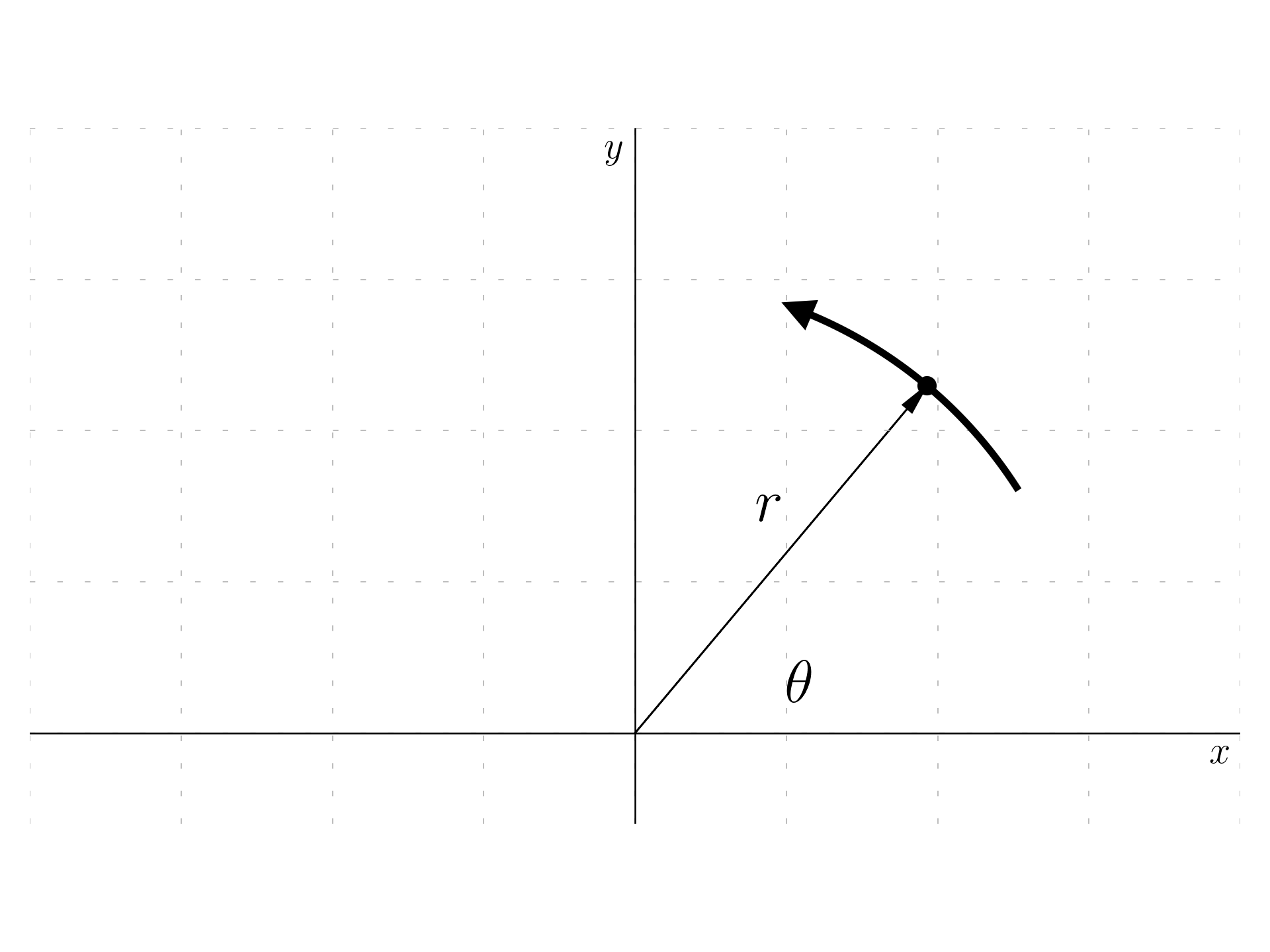
The Lagrangian is:

\mathcal L = \frac{m}{2} (\dot x^2 + \dot y^2) - V(x^2 + y^2)

The symmetry is natural a rotation around the origin of an angle \theta.

To study this problem it is possible to rotate the coordinates of the particle by an angle \theta; the new coordinates become:

\begin{array}{c} x' = x \, \cos(\theta) - y \, \sin(\theta) \\ y' = x \, \sin(\theta) + y \, \cos(\theta) \end{array}

It is possible to apply an infinitesimal change \varepsilon to the angle and compute the change; then it is possible to have a finite change as the sum of infinitesimal changes; these are called continuous transformations.

It is possible to set \theta = \varepsilon, expand the trigonometric function in Taylor series and consider order up to \varepsilon:

\begin {aligned} & \cos(\varepsilon) = 1 - \dfrac{\varepsilon^2}{2} + \cdots = 1 + \mathcal O (\varepsilon^2) \\ & \sin(\varepsilon) = \varepsilon -\frac{\varepsilon^3}{6} + \cdots = \varepsilon + \mathcal O (\varepsilon^3) \end{aligned}

Plug into the coordinate change:

\begin{array}{c} x' = x - y \,\varepsilon \\ y' = x \, \varepsilon + y \end{array}

therefore:

\begin{array}{c} \delta x = - y\,\varepsilon \\ \delta y = x\,\varepsilon \end{array}

Similarly the velocity changes as:

\begin{array}{c} \delta \dot x = - \dot y\,\varepsilon \\ \delta \dot y = \dot x\,\varepsilon \end{array}

With these transformations, it is possible to check that the Lagrangian does not change:

\begin{aligned} \mathcal L & = \frac{m}{2} (\dot x'^2 + \dot y'^2) - V\left(x'^2 + y'^2 \right) \\ & = \frac{m}{2} \left((\dot x-\dot y\varepsilon)^2 + (\dot y+\dot x\varepsilon)^2 \right) - V\left((x-y\varepsilon)^2 + (y+x\varepsilon)^2 \right) \\ & = \frac{m}{2} \left(\dot x^2 - 2 \dot x \, \dot y \, \varepsilon + \dot y^2\varepsilon^2 + \dot y^2 + 2 \dot y \, \dot x \, \varepsilon + \dot x^2\varepsilon^2 \right) - V\left(x^2 - 2 x\,y \varepsilon + y^2\varepsilon^2 + y^2 + 2 x\,y\,\varepsilon + x^2\varepsilon^2 \right) \\ & = \frac{m}{2} \left(\dot x^2 + \dot y^2 + \mathcal O(\varepsilon^2) \right) - V\left(x^2 + y^2 + \mathcal O(\varepsilon^2) \right)\\ & = \frac{m}{2} \left(\dot x^2 + \dot y^2 \right) - V\left(x^2 + y^2 \right) \end{aligned}

As terms \mathcal O (\varepsilon^2) are not considered.

Exercise 7.5

The exercise has been analyzed in details in a specific page here.

Exercise 7.6

The exercise has been analyzed in details in a specific page here.

Exercise 7.7

The exercise has been analyzed in details in a specific page here.

Go to the top of the page