Exercise list
Lecture 1
Interlude 1
Lecture 2
Interlude 2
Lecture 3
Interlude 3
Lecture 1
Exercise 1.1
Since the notion is so important to theoretical physics, think about what a closed system is, and speculate on whether closed systems can actually exist. What assumptions are implicit in establishing a closed system? What is an open system?
A closed system in theoretical physics is defined as a system that does not exchange matter with its surroundings but may exchange energy. This concept is crucial in simplifying the study of complex systems by isolating them from external influences, making it possible to apply the laws of physics in a more controlled and predictable manner. The existence of perfectly closed systems, however, is more theoretical than practical, as it is nearly impossible to completely isolate a system from all external matter exchange in reality. The assumptions implicit in establishing a closed system include the constancy of mass within the system and the negligible effect of external forces or matter on the system’s internal processes. These assumptions allow for the application of conservation laws, such as the conservation of mass and energy, facilitating the analysis and prediction of the system’s behavior over time.
Open systems, in contrast, are those that freely exchange energy and matter with their environment. This exchange introduces a level of complexity in analyzing the system’s behavior, as it is influenced by a potentially unpredictable external environment. The concept of open systems is more aligned with real-world scenarios where interactions with surroundings are commonplace, such as biological systems or planetary atmospheres. Open systems require a more dynamic approach to study, often involving the analysis of fluxes of matter and energy across system boundaries and how these exchanges affect the system’s internal state.
The distinction between closed and open systems highlights the fundamental assumptions and simplifications made in physics to understand the natural world. While closed systems offer a simplified model for theoretical exploration, the reality is often more accurately described by open systems, which necessitate a consideration of external interactions. This realization underscores the importance of context in the application of physical laws and the understanding that all models and systems in physics are approximations designed to fit the complexity of the universe into manageable frameworks for study.
Exercise 1.2
Can you think of a general way to classify the laws that are possible for a six-state system?
For classifying laws in a six-state system, consider each state as a node in a graph with directed edges indicating transitions. The system adheres to a rule where each state has exactly one incoming and one outgoing edge, creating a network of cycles. Classification begins by identifying these cycles, which vary in length and can encapsulate one or more states, providing a macro view of the system’s structure.
Further refinement is achieved by examining cycles within cycles, akin to nested loops, offering insights into the system’s finer dynamics. This method acknowledges both the overarching connectivity and the detailed pathways between states, offering a comprehensive framework for understanding the system’s behavior through its cycles and sub-cycles.
Exercise 1.3
Determine which of the dynamical laws shown in Eq.s (2) through (5) are allowable.
N(n+1) = N(n)-1
Given the dynamical laws N(n+1) = N(n) - 1:
This law decrements the state by 1 at each step. Given any state N(n+1), we can directly find the previous state N(n) by adding 1. This relationship clearly defines a one-to-one mapping between N(n) and N(n+1), ensuring that for every state, there is a unique predecessor. Therefore, this law is reversible.
N(n+1) = N(n)+2
Given the dynamical laws N(n+1) = N(n) + 2:
This law increments the state by 2 at each step. Given any state N(n+1), the previous state N(n) can be uniquely determined by subtracting 2. This operation also establishes a one-to-one correspondence between N(n) and N(n+1), indicating that the law allows for the unique determination of N(n) from N(n+1) and is thus reversible.
N(n+1) = N(n)^2
Given the dynamical law N(n+1) = N(n)^2:
This law squares the state at each step. Analyzing its behavior:
- If N(n) > 1 or N(n) < -1, squaring N(n) results in a larger positive value for N(n+1), making the process irreversible since multiple values of N(n) could lead to the same N(n+1) upon squaring (both a positive and a negative root).
- If N(n) = 1, N(n+1) = 1, which is a stable state.
- If N(n) = 0, N(n+1) = 0, which is another stable state.
- If N(n) = -1, N(n+1) = 1, transitioning to the stable state without a reversible path back to -1.
Given the squared relationship, for any N(n+1) > 1, there are two possible predecessors (\sqrt{N(n+1)} and -\sqrt{N(n+1)}), except for the special cases where N(n+1) = 1 or N(n+1) = 0, where the predecessor is uniquely determined. This analysis shows that the law is not generally reversible, as it does not always allow for a unique determination of N(n) from N(n+1), except in specific cases like N(n+1) = 1 or N(n+1) = 0.
N(n+1) = -1^{N(n)}N(n)
Given the dynamical law N(n+1) = (-1)^{N(n)}N(n):
- For N(n) = 0, N(n+1) = (-1)^0 \cdot 0 = 0, indicating a stable, unchanged state.
- For N(n) = 1, the pattern alternates between 1 and -1, as N(n+1) = (-1)^1 \cdot 1 = -1, and then applying the law again leads back to 1, indicating a reversible cycle between 1 and -1.
- For a general N(n) = k, N(n+1) = (-1)^k \cdot k, which will be k if k is even (since (-1)^k = 1 for even k) or -k if k is odd (since (-1)^k = -1 for odd k), showcasing an alternation between k and -k for odd values of k.
This analysis demonstrates that, for any value of N(n), the future state N(n+1) is deterministically defined and the previous state N(n) can be inferred from N(n+1), confirming the law’s reversibility.
Interlude 1
Exercise I1.1
Using a graphic calculator or a program like Mathematica, plot each of the following functions. See the next section if you are unfamiliar with the trigonometric functions.
\begin{aligned} & f(t) = t^4 + 3t^3 - 12 t^2 + t - 6 \\ & g(x) = \sin(x) - \cos(x) \\ & \theta(\alpha) = e^{\alpha} + \alpha \ln(\alpha) \\ & x(t) = \sin(x)^2 - \cos(x) \end{aligned}
The functions are plotted using Python.
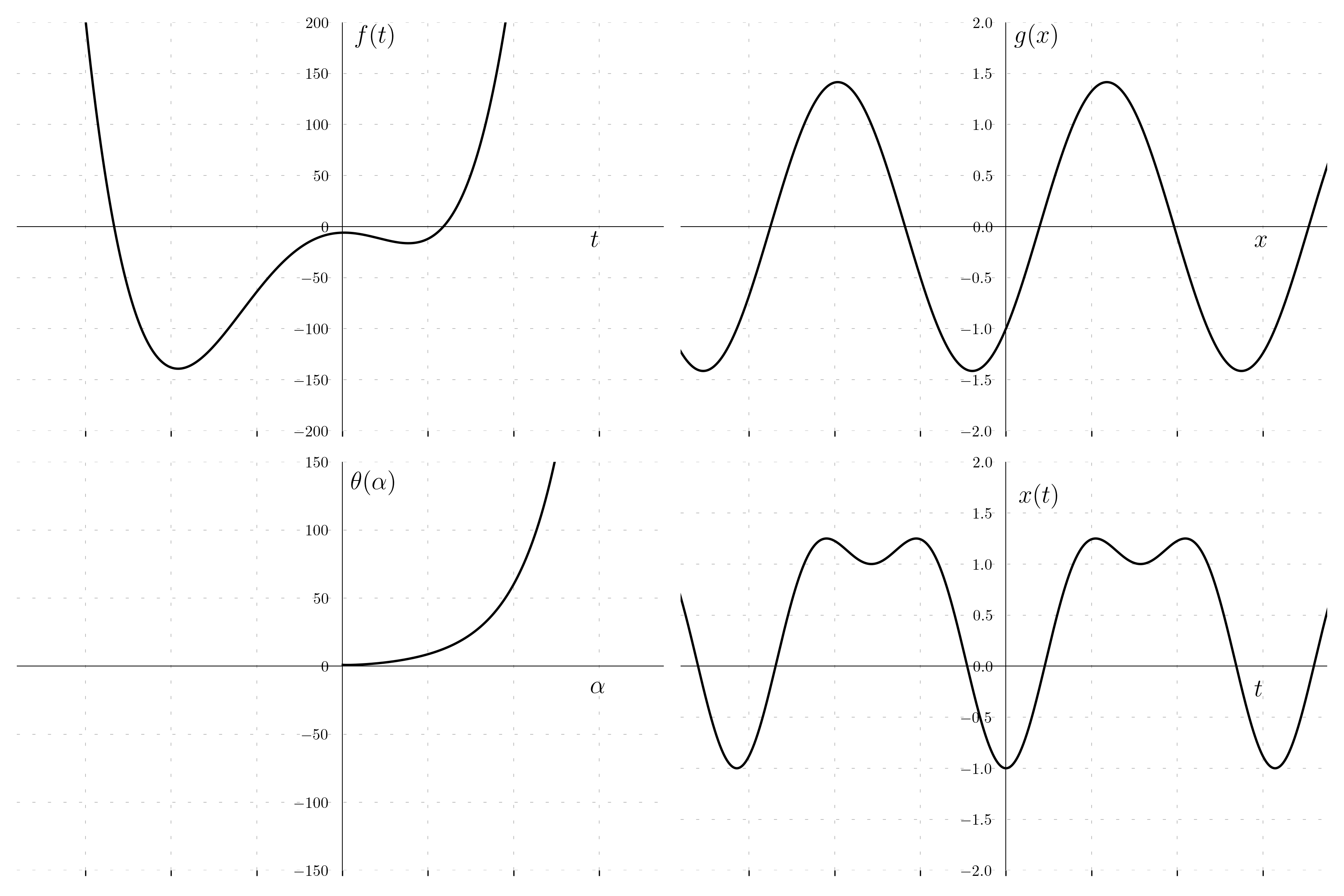
Exercise I1.2
Work out the rule for vector subtraction.
It is possible to work out the rule for vector subtraction completing the triangle which goes from the end of vector \mathbf B to the end of the vector \mathbf A.
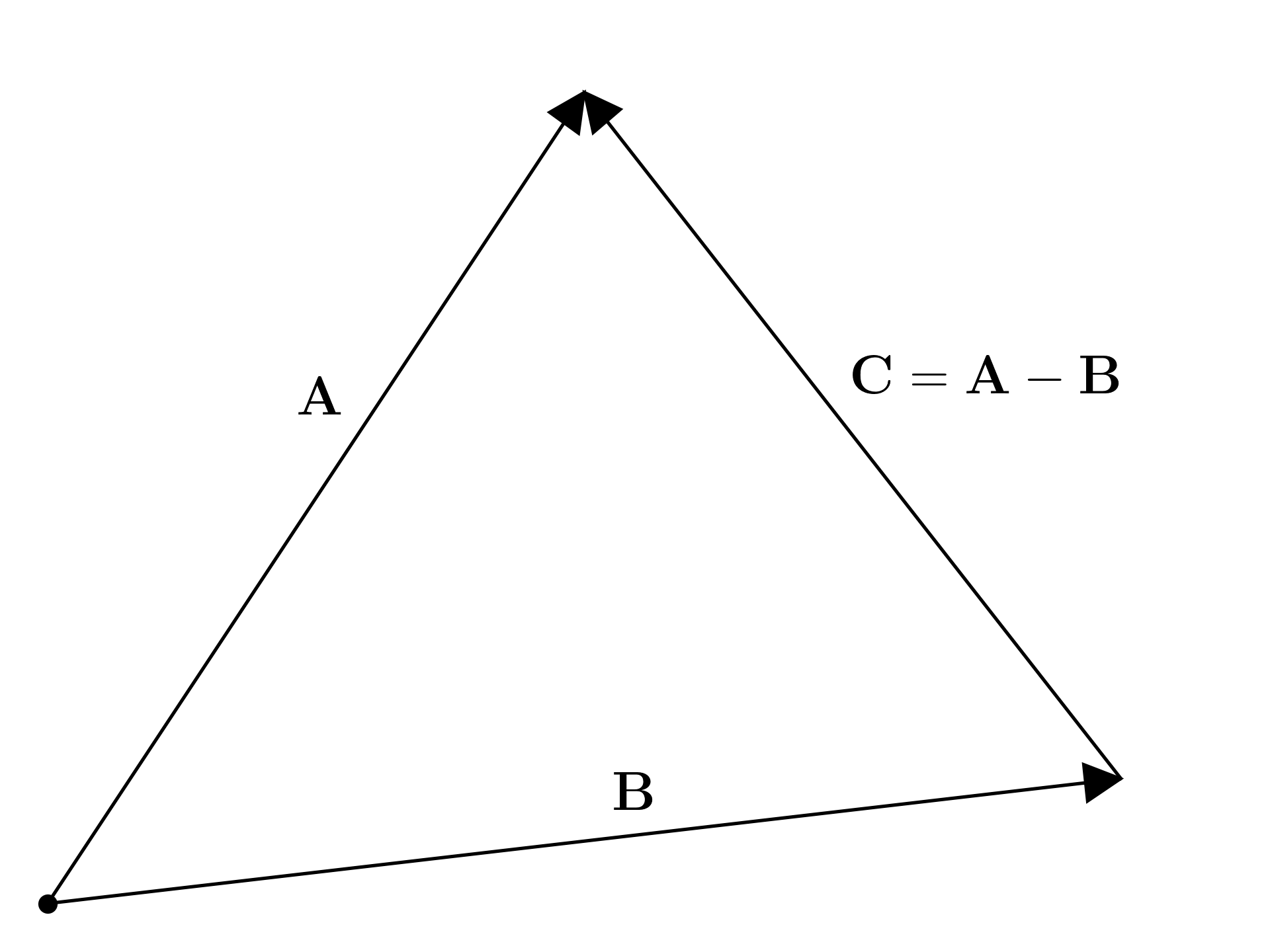
Noting that this vector \mathbf C satisfy the sum:
\mathbf B + \mathbf C = \mathbf A
subtracting \mathbf B from both sides:
\mathbf C = \mathbf A - \mathbf B
Exercise I1.3
Show that the magnitude of a vector satisfies:
\mathbf{A} \cdot \mathbf{A} = |\mathbf{A}|^2
Using the definition of the dot product and the magnitude of a vector; the dot product of \mathbf{A} with itself is:
\mathbf{A} \cdot \mathbf{A} = A_x^2 + A_y^2 + A_z^2
where A_x, A_y, A_z are the components of \mathbf{A}.
The magnitude |\mathbf{A}| of vector \mathbf{A} is defined as:
|\mathbf{A}| = \sqrt{A_x^2 + A_y^2 + A_z^2}
Squaring the magnitude gives:
|\mathbf{A}|^2 = (\sqrt{A_x^2 + A_y^2 + A_z^2})^2 = A_x^2 + A_y^2 + A_z^2
Therefore, \mathbf{A} \cdot \mathbf{A} = |\mathbf{A}|^2.
Exercise I1.4
Let (A_x = 2, A_y = -3, A_z = 1 and B_x = -4, B_y = -3, B_z = 2). Compute the magnitude of \mathbf A and \mathbf B, their dot product and the angle between them.
Considering the vectors:
\mathbf A = [2, -3, 1] \quad \mathbf B = [-4, -3, 2] Then:
\begin{aligned} & |\mathbf A| = \sqrt{2^2 +(-3)^3 + 1} = \sqrt{14} \approx 3.7416 \\ & |\mathbf B| = \sqrt{(-4)^2 + (-3)^2 + 2^2} = \sqrt{29} \approx 5.3851 \\ & \mathbf A \cdot \mathbf B = 2 \times (-4) + (-3) \times (-3) + 1 \times 2 = 3 \\ & \theta = \arccos \left(\frac{\mathbf A \cdot \mathbf B}{|\mathbf A| |\mathbf B|}\right) = \arccos\left( \frac{3}{\sqrt 406} \right) \approx \arccos(0.1489) \approx 1.421353189\; \text{rad} \approx 81.437^\circ \end{aligned}
Exercise I1.5
Determine which pair of vectors are orthogonal. (1,1,1) (2,-1,3) (3,1,0) (-3,0,2)
Considering the vectors:
\mathbf A = [1, 1, 1] \quad \mathbf B = [2, -1, 3] \quad \mathbf C = [3, 1, 0] \quad \mathbf D = [-3, 0, 2] To check the orthogonality of these, computing the dot products:
\begin{aligned} & \mathbf A \cdot \mathbf B = 1 \times 2 + 1 \times (-1) + 1 \times 3 = 4 \\ & \mathbf A \cdot \mathbf C = 1 \times 3 + 1 \times 1 + 1 \times 0 = 4 \\ & \mathbf A \cdot \mathbf D = 1 \times (-3) + 1 \times 0 + 1 \times 2 = 1\\ & \mathbf B \cdot \mathbf C = 2 \times 3 + (-1) \times 1 + 3 \times 0 = 5 \\ & \mathbf B \cdot \mathbf D = 2 \times (-3) + (-1) \times 0 + 3 \times 2 = 0\\ & \mathbf C \cdot \mathbf D = 3 \times (-3) + 1 \times 0 + 0 \times 2 = -9 \end{aligned}
Therefore only \mathbf B and \mathbf D are orthogonal.
Exercise I1.6
Can you explain why the dot product of two vectors that are orthogonal is 0?
The dot product of two vectors \mathbf{A} and \mathbf{B} is given by:
\mathbf{A} \cdot \mathbf{B} = |\mathbf{A}| |\mathbf{B}| \cos(\theta)
where \theta is the angle between the vectors.
When two vectors are orthogonal, the angle between them is \frac{\pi}{2} radians, which have cosine equal to 0. Therefore:
\mathbf{A} \cdot \mathbf{B} = |\mathbf{A}| |\mathbf{B}| \cos\left(\frac{\pi}{2}\right) = |\mathbf{A}| |\mathbf{B}| \times 0 = 0
Hence, the dot product of two orthogonal vectors is zero.
Lecture 2
Exercise 2.1
Calculate the derivatives of each of these functions.
\begin{aligned} & f(t) = t^4 + 3t^3 - 12 t^2 + t - 6 \\ & g(x) = \sin(x) - \cos(x) \\ & \theta(\alpha) = e^{\alpha} + \alpha \ln(\alpha) \\ & x(t) = \sin(x)^2 - \cos(x) \end{aligned}
The derivatives are:
\begin{aligned} & \tfrac{\mathrm d f(t)}{\mathrm dt} = 4t^3 + 9t^2 - 24 t + 1 \\ & \tfrac{\mathrm d g(x)}{\mathrm dx} = \sin(x) + \cos(x) \\ & \tfrac{\mathrm d theta(\alpha)}{\alpha} = e^{\alpha} + \ln(\alpha) + 1 \\ & \tfrac{\mathrm d x(t)}{\mathrm dt} = \sin(t)(2\cos(t) + 1) \end{aligned}
Exercise 2.2
The derivative of a derivative is called the second derivative and it is written as \frac{\mathrm d^2 f(t)}{\mathrm dt^2}. Take the second derivative of each of the functions listed above.
The second derivative of the functions of the previous exercise are:
\begin{aligned} & \tfrac{\mathrm d^2 f(t)}{\mathrm dt^2} = 12t^2 + 18t - 24 \\ & \tfrac{\mathrm d^2 g(x)}{\mathrm dx^2} = \cos(x) - \sin(x) \\ & \tfrac{\mathrm d^2 theta(\alpha)}{\alpha^2} = e^{\alpha} + \tfrac{1}{\alpha} \\ & \tfrac{\mathrm d^2 x(t)}{\mathrm dt^2} = 2\cos(t)^2 - 2\sin(t)^2 + \cos(t) \end{aligned}
Exercise 2.3
Use the chain rule to find the derivative of each of the following functions:
\begin{aligned} & g(t) = \sin(t^2) - \cos(t^2) \\ & \theta(\alpha) = e^{3\alpha} + 3\alpha \ln(3\alpha) \\ & x(t) = \sin(t^2)^2 - \cos(t^2) \end{aligned}
The derivatives are:
\begin{aligned} & \tfrac{\mathrm d g(t)}{\mathrm dt} = 2t\left(\sin(t^2) + \cos(t^2)\right) \\ & \tfrac{\mathrm d theta(\alpha)}{\alpha} = 3e^{3\alpha} + 3\ln(3\alpha) + 9 \\ & \tfrac{\mathrm d x(t)}{\mathrm dt} = 2t\sin(t^2)\left(2\cos(t^2) + 1\right) \end{aligned}
Exercise 2.4
Prove the sum rule (fairly easy), the product rule (fairly easy if you know the trick) and the chain rule (fairly easy).
The sum rule states that for two differentiable functions f(x) and g(x), the derivative of their sum is given by:
\frac{\mathrm d}{\mathrm dx}(f(x) + g(x)) = f'(x) + g'(x)
- The derivative of a function h(x) at a point x is defined as:
h'(x) = \lim_{\Delta x \to 0} \frac{h(x + \Delta x) - h(x)}{\Delta x}
For the sum of two functions f(x) and g(x), we have h(x) = f(x) + g(x).
- Apply the Definition to f(x) + g(x):
\frac{\mathrm d}{\mathrm dx}(f(x) + g(x)) = \lim_{h \to 0} \frac{(f(x+h) + g(x+h)) - (f(x) + g(x))}{h}
- Simplify the expression in the limit:
\frac{\mathrm d}{\mathrm dx}(f(x) + g(x)) = \lim_{h \to 0} \frac{f(x+h) - f(x) + g(x+h) - g(x)}{h}
- Splitting the Limit; The limit of a sum is the sum of the limits (if they exist):
\frac{\mathrm d}{\mathrm dx}(f(x) + g(x)) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} + \lim_{h \to 0} \frac{g(x+h) - g(x)}{h}
- Each term in the expression is now the definition of the derivative of $ f $ and $ g $ respectively:
\frac{\mathrm d}{\mathrm dx}(f(x) + g(x)) = \frac{\mathrm df(x)}{\mathrm dx} + \frac{\mathrm dg(x)}{\mathrm dx}
Thus, the derivative of the sum f(x) + g(x) is the sum of their derivatives. This completes the proof.
The product rule which states that for two differentiable functions f(x) and g(x), the derivative of their product is given by:
\frac{\mathrm d}{\mathrm dx}(f(x) \cdot g(x)) = f(x) \cdot g'(x) + f'(x) \cdot g(x)
- The derivative of a function h(x) at a point x is defined as:
h'(x) = \lim_{\Delta x \to 0} \frac{h(x + \Delta x) - h(x)}{\Delta x}
For the product of two functions f(x) and g(x), we have h(x) = f(x) \cdot g(x).
- Apply the Definition to f(x) \cdot g(x):
\frac{\mathrm d}{\mathrm dx}(f(x) \cdot g(x)) = \lim_{h \to 0} \frac{(f(x+h) \cdot g(x+h)) - (f(x) \cdot g(x))}{h}
- Introduce a term f(x) \cdot g(x+h) to facilitate the breakdown which is added and subtracted:
\frac{\mathrm d}{\mathrm dx}(f(x) \cdot g(x)) = \lim_{h \to 0} \frac{f(x+h) \cdot g(x+h) - f(x) \cdot g(x+h) + f(x) \cdot g(x+h) - f(x) \cdot g(x)}{h}
- Rearrange Terms, grouping the terms to recognize the derivative formulas:
\frac{\mathrm d}{\mathrm dx}(f(x) \cdot g(x)) = \lim_{h \to 0} \left[ \frac{f(x+h) \cdot g(x+h) - f(x) \cdot g(x+h)}{h} + \frac{f(x) \cdot g(x+h) - f(x) \cdot g(x)}{h} \right]
- Split this into two limits and recognize the derivative definitions:
\frac{\mathrm d}{\mathrm dx}(f(x) \cdot g(x)) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \cdot g(x+h) + f(x) \cdot \lim_{h \to 0} \frac{g(x+h) - g(x)}{h}
- Apply the Limit, since f(x) and g(x) are differentiable, apply the limit:
\frac{\mathrm d}{\mathrm dx}(f(x) \cdot g(x)) = f'(x) \cdot g(x) + f(x) \cdot g'(x)
This completes the proof of the product rule.
The chain rule states that two functions f(x) and g(x) where f(x) is differentiable at x and g(y) is differentiable at f(x), then the composite function (g \circ f)(x) = g(f(x)) is differentiable at x, and its derivative is given by:
\frac{\mathrm d}{\mathrm dx} g(f(x)) = g'(f(x)) \cdot f'(x)
- The derivative of a function h(x) at a point x is defined as:
h'(x) = \lim_{\Delta x \to 0} \frac{h(x + \Delta x) - h(x)}{\Delta x}
-
Introducing a variable k = f(x + h) - f(x). Notice that as h \to 0, k \to 0 since f is differentiable (and hence continuous) at x.
-
Rewrite the Limit in Terms of k, the derivative becomes:
\frac{\mathrm d}{\mathrm dx} g(f(x)) = \lim_{h \to 0} \frac{g(f(x) + k) - g(f(x))}{h}
-
Express h as a function of k. This is the tricky part and requires the assumption that f'(x) \neq 0 so that we can invert k as a function of h. This gives h(k).
-
Apply the Chain Rule and change the limit variable from h to k:
\frac{\mathrm d}{\mathrm dx} g(f(x)) = \lim_{k \to 0} \frac{g(f(x) + k) - g(f(x))}{h(k)}
- Using the definition of the derivative for g, the limit is the derivative of g at f(x):
\frac{\mathrm d}{\mathrm dx} g(f(x)) = g'(f(x)) \cdot \lim_{k \to 0} \frac{k}{h(k)}
- Recognize f'(x) in the limit: the limit \lim_{k \to 0} \frac{k}{h(k)} is essentially the definition of f'(x), hence:
\frac{\mathrm d}{\mathrm dx} g(f(x)) = g'(f(x)) \cdot f'(x)
This completes the proof of the chain rule.
Exercise 2.5
Prove each of the formulas in Eq.s (2). Hint: Look up trigonometric identities and limit properties in a reference book
\sin(t)
Using the identity \sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B):
and:
\begin{gathered} \lim\limits_{h \to 0} \frac{(1 - \cos(h))}{h} = 0 \\ \lim\limits_{h \to 0} \frac{\sin(h)}{h} = 1 \end{gathered}
Applying the definition:
\begin{aligned} \frac{\mathrm{d}f(t)}{\mathrm{d}t} & = \lim\limits_{h \rightarrow 0} \frac{\sin(t + h) - \sin(t)}{h} \\ & = \lim\limits_{h \to 0} \frac{\sin(t)\cos(h) + \cos(t)\sin(h) - \sin(t)}{h} \\ & = \lim\limits_{h \to 0} \frac{\sin(t)(1 - \cos(h)) + \cos(t)\sin(h)}{h} \\ & = \lim\limits_{h \to 0} \frac{\sin(t)(1 - \cos(h))}{h} + \lim\limits_{h \to 0} \frac{\cos(t)\sin(h)}{h} \\ & = \cos(t) \\ \end{aligned}
\cos(t)
Using the identity \cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B):
and
\begin{gathered} \lim\limits_{h \to 0} \frac{(1 - \cos(h))}{h} = 0 \\ \lim\limits_{h \to 0} \frac{\sin(h)}{h} = 1 \end{gathered}
Applying the definition:
\begin{aligned} \frac{\mathrm{d}f(t)}{\mathrm{d}t} & = \lim\limits_{h \rightarrow 0} \frac{\cos(t + h) - \cos(t)}{h} \\ & = \lim\limits_{h \to 0} \frac{\cos(t)\cos(h) - \sin(t)\sin(h) - \cos(t)}{h} \\ & = \lim\limits_{h \to 0} \frac{\cos(t)(\cos(h) - 1) - \sin(t)\sin(h)}{h} \\ & = \lim\limits_{h \to 0} \frac{-\cos(t)(1 - \cos(h)) - \sin(t)\sin(h)}{h} \\ & = -\sin(t) \\ \end{aligned}
e^t
From the definition of e^t as (taking n=\frac{1}{h} and t=1):
e^t = \lim\limits_{n \to \infty} \left( 1 + \frac{t}{n} \right)^n = \lim\limits_{h \to 0} (1 + th)^{\frac{1}{h}}
Applying the definition:
\begin{aligned} \frac{\mathrm{d}f(t)}{\mathrm{d}t} & = \lim\limits_{h \rightarrow 0} \frac{e^{t + h} - e^t}{h} \\ & = \lim\limits_{h \to 0} \frac{e^te^h - e^t}{h} \\ & = \lim\limits_{h \to 0} \frac{ e^t (e^h - 1) }{h} \\ & = e^t \lim\limits_{h \to 0} \frac{e^h -1}{h} \\ & = e^t \lim\limits_{h \to 0} \frac{\left((1 + h)^{\frac{1}{h}}\right)^h - 1}{h} \\ & = e^t \lim\limits_{h \to 0} \frac{\left( 1 + h \right) - 1}{h} \\ & = e^t \end{aligned}
\ln(t)
From the definition of e^t as (taking n=\frac{1}{h}):
e^{\frac{1}{t}} = \lim\limits_{n \to \infty} \left( 1 + \frac{1}{t} \frac{1}{n} \right)^n = \lim\limits_{h \to 0} (1 + \frac{h}{t})^{\frac{1}{h}}
Applying the definition:
\begin{aligned} \frac{\mathrm{d}f(t)}{\mathrm{d}t} & = \lim\limits_{h \rightarrow 0} \frac{\ln(t + h) - \ln(t)}{h} \\ & = \lim\limits_{h \to 0} \frac{\ln \left( \frac{t+h}{t} \right)}{h} \\ & = \lim\limits_{h \to 0} \ln \left( \frac{t+h}{t} \right)^{\frac{1}{h}} \\ & = \lim\limits_{h \to 0} \ln \left( 1 + \frac{h}{t} \right)^{\frac{1}{h}} \\ & = \ln \left( e^{\frac{1}{t}} \right) \\ & = \frac{1}{t} \end{aligned}
Exercise 2.6
How long does it takes for the oscillating particle to go through one full cycle of motion?
Since the equation of motion is described by:
x(t) = \sin\left(\omega \,t\right) which is a periodic trigonometric functions which have a period 2\,\pi, to go through a full cycle it takes:
\omega\,T = 2\pi \quad \Rightarrow \quad T = \frac{2\,\pi}{\omega}
Exercise 2.7
Show that the position and the velocity are orthogonal.
The most general form of a counterclockwise uniform circular motion has the formulation:
\begin{aligned} & x(t) = R \cos(\omega t) \\ & y(t) = R \sin(\omega t) \end{aligned}
The parameter \omega is the angular frequency. It is easy to calculate now the velocity and acceleration by differentiating:
\begin{aligned} & v_x(t) = -R \omega \sin(\omega t) \\ & v_y(t) = R \omega \cos(\omega t) \\ & a_x(t) = -R^2 \omega^2 \cos(\omega t) \\ & a_y(t) = -R^2 \omega^2 \sin(\omega t) \end{aligned}
The acceleration of a circular orbit is parallel to the position vector but it is oppositely directed and therefore it point radially inward towards the origin; furthermore, the position and the velocity vectors are orthogonal:
\mathbf r \, \mathbf v = x\,v_x + y\,v_y = R \cos(\omega t)(-R \omega \sin(\omega t)) + R \sin(\omega t) R \omega \sin(\omega t) = -R^2\cos(\omega t)\sin(\omega t) + R^2\cos(\omega t)\sin(\omega t) = 0
Since the inner product is zero, the two vector are orthogonal; since the position and the acceleration are collinear, it means that the velocity is also orthogonal to the acceleration. The magnitude of the velocity is \omega (\left|v^2\right| = \left| \omega^2\left[\cos(\omega t)^2 + \sin(\omega t)^2\right] \right| = \left| \omega^2 \right|) and the magnitude of the acceleration is \omega^2 (\left|a^2\right| = \left| \omega^4\left[\cos(\omega t)^2 + \sin(\omega t)^2\right] \right| = \left| \omega^4 \right|).
Exercise 2.8
Calculate the velocity, speed and acceleration for each of the following position vectors. If you have graphing software, plot each position vector, each velocity vector, and each acceleration vector.
\begin{aligned} & \mathbf r = (\cos(\omega \, t), e^{\omega t}) \\ & \mathbf r = (\cos(\omega\,t-\phi), \sin(\omega\,t - \phi)) \\ & \mathbf r = (c\cos(t)^3, c \sin(t)^3) \\ & \mathbf r = (c(t-\sin(t)), c(1 - \cos(t))) \end{aligned}
\mathbf r = (\cos(\omega \, t), e^{\omega t})
Considering the vector:
\mathbf r = (\cos(\omega \, t), e^{\omega t})
The velocity and the acceleration are:
\begin{aligned} & v_x(t) = - \omega \sin(\omega t) \\ & v_y(t) =\omega e^{\omega \,t } \\ & a_x(t) = -\omega^2 \cos(\omega t) \\ & a_y(t) = \omega^2 e^{\omega \,t } \end{aligned}
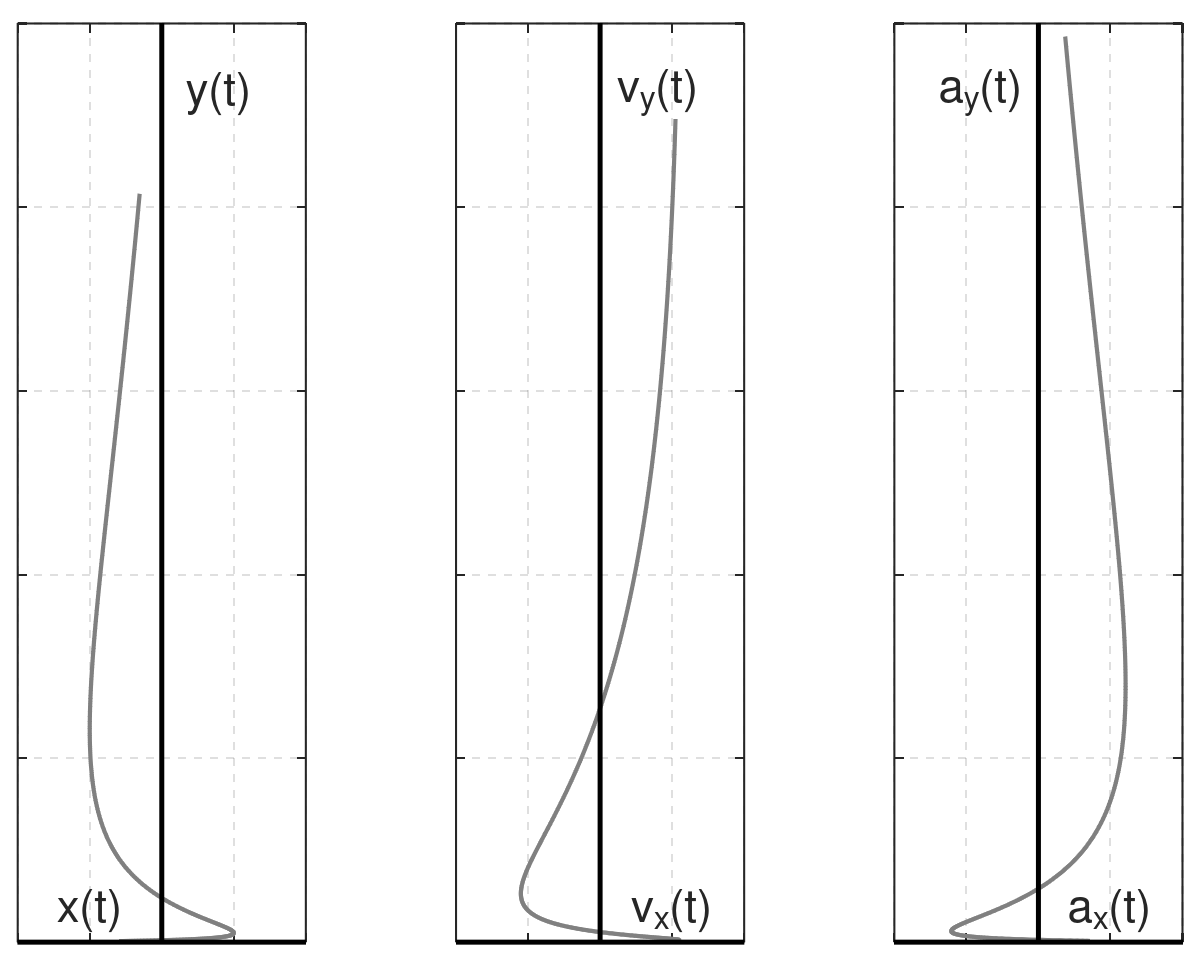
A video with \omega = 1.2, and 0 < t < 20 is shown below:
\mathbf r = (\cos(\omega\,t-\phi), \sin(\omega\,t - \phi))
Considering the vector:
\mathbf r = (\cos(\omega\,t-\phi), \sin(\omega\,t - \phi))
The velocity and the acceleration are:
\begin{aligned} & v_x(t) = - \omega \sin(\omega t -\phi) \\ & v_y(t) = \omega \cos(\omega t -\phi) \\ & a_x(t) = - \omega^2 \cos(\omega t -\phi) \\ & a_y(t) = - \omega^2 \sin(\omega t -\phi) \end{aligned}
The parameter \phi in the equations represents a phase shift in the harmonic motion.
- When \phi = 0, the motion starts at the origin (t = 0) with the vector \mathbf{r} = (\cos(0), \sin(0)) = (1, 0).
- When \phi is non-zero, it introduces a delay or advancement in the starting position of the motion. For instance, with \phi = 1, the motion’s initial phase is shifted, so it will pass through the origin at a later time, specifically at t = \frac{1}{\omega}.
This phase shift doesn’t change the nature or the frequency of the motion; it merely alters the starting point in the cycle.
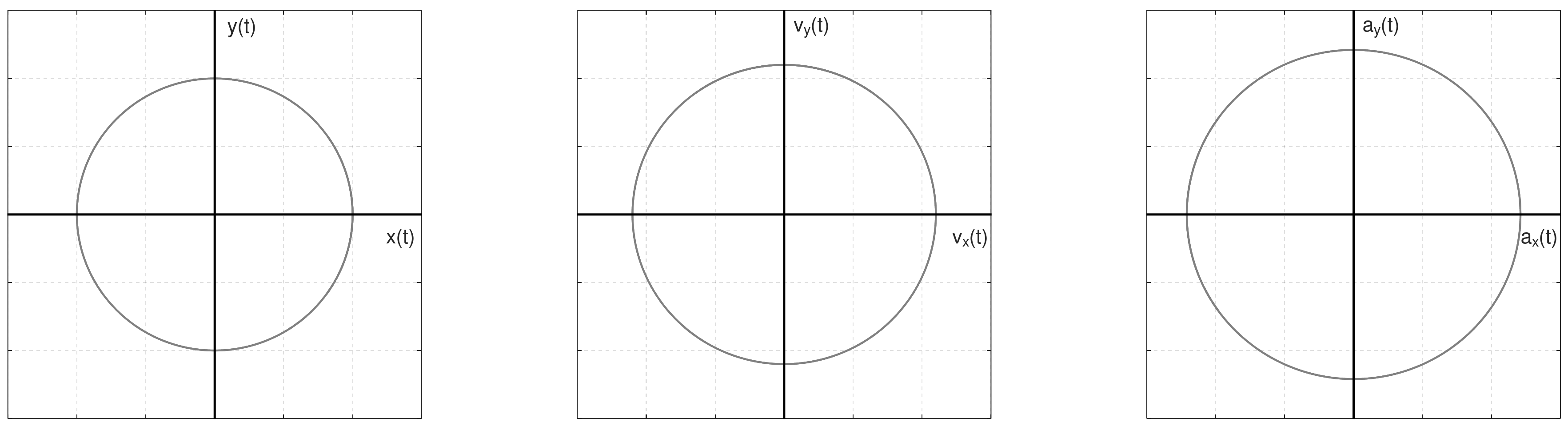
A video with \omega = 1.2, \phi = 0.8, and 0 < t < 2\pi is shown below:
\mathbf r = (c\cos(t)^3, c \sin(t)^3)
Considering the vector:
\mathbf r = (c\cos(t)^3, c \sin(t)^3)
The velocity and the acceleration are:
\begin{aligned} & v_x(t) = -3\,c\cos(t)^2\sin(t)\\ & v_y(t) = 3\,c\sin(t)^2\cos(t) \\ & a_x(t) = 6\,c\cos(t)\sin(t)^2 -3\,c \cos(t)^3\\ & a_y(t) = 6\,c\sin(t)\cos(t)^2-3\,c \sin(t)^3 \end{aligned}
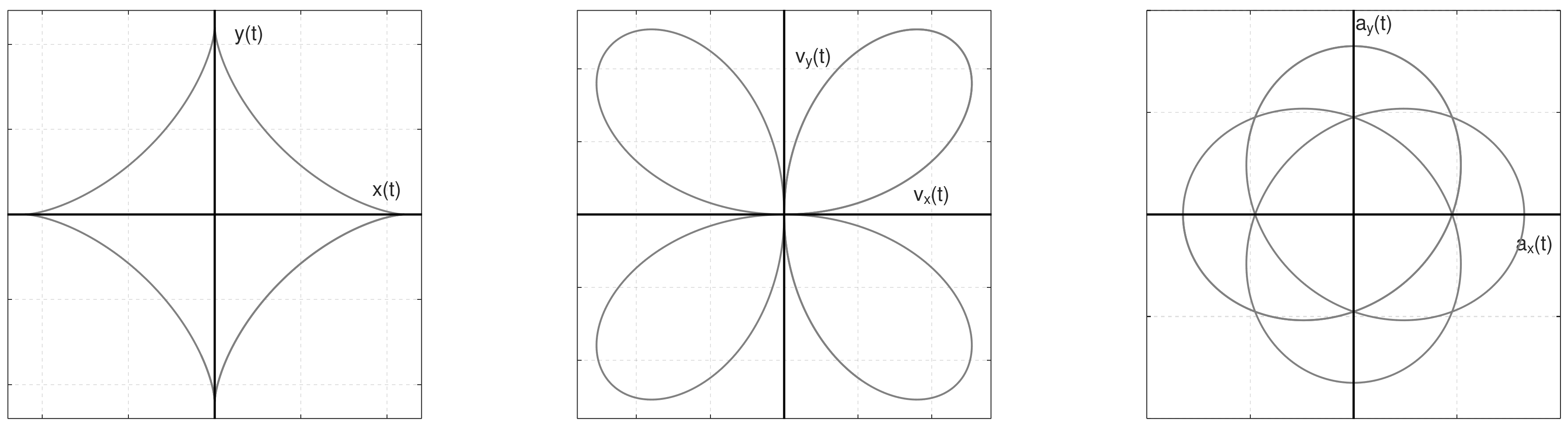
A video with \c = 1.2, and 0 < t < 2\pi is shown below:
\mathbf r = (c(t-\sin(t)), c(1 - \cos(t)))
Considering the vector:
\mathbf r = (c(t-\sin(t)), c(1 - \cos(t)))
The velocity and the acceleration are:
\begin{aligned} & v_x(t) = c(1-\cos(t)) \\ & v_y(t) = c\sin(t) \\ & a_x(t) = -c\sin(t) \\ & a_y(t) = -c\cos(t) \end{aligned}
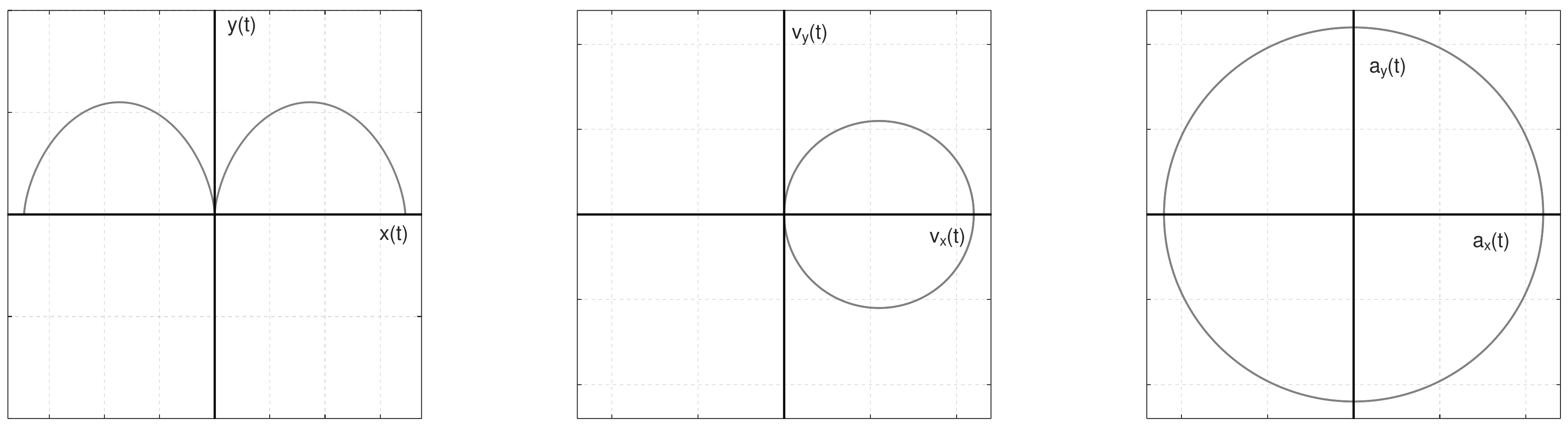
A video with \c = 1.2, and -2\pi < t < 2\pi is shown below:
Exercise I2.1
Determine the indefinite integral of each of the following expressions by reversing the process of differentiation and adding a constant. \begin{aligned} & f(t) = t^4 \\ & f(t) = \cos(t) \\ & f(t) = t^2 - 2 \end{aligned}
\begin{aligned} & \int t^4 \mathrm dt = \frac{t^5}{5} + C \\ & \int \cos(t) \mathrm dt = \sin(t) + C \\ & \int \left( t^2 - 2\right) \mathrm dt = \frac{t^3}{3} -2t + C \end{aligned}
Exercise I2.2
Use the fundamental theorem of calculus to evaluate each integral from Exercise 1 with limits of integration being t=0 to t=T.
\begin{aligned} & \int_0^T t^4 \mathrm dt = \frac{t^5}{5} \bigg|_0^T = \frac{T^5}{5} \\ & \int_0^T \cos(t) \mathrm dt = \sin(t) \bigg|_0^T = \sin(T) \\ & \int_0^T \left( t^2 - 2\right) \mathrm dt = \left[\frac{t^3}{3} -2t \right]\bigg|_0^T = \frac{T^3}{3} -2T \end{aligned}
Exercise I2.3
Treat the expressions from Exercise 1 as expressions for the acceleration of a particle. Integrate them once, with respect to time, and determine the velocities, and a second time to determine the trajectories. Because we will use t as one of the limits of integration we will adopt the dummy integration variable t'. Integrate them from t'=0 to t'=t. \begin{aligned} & v(t) = \int_0^t {t'}^4 \mathrm dt'\\ & v(t) =\int_0^t \cos(t') \mathrm dt'\\ & v(t) \int_0^t \left( {t'}^2 - 2\right) \mathrm dt' \end{aligned}
Starting to compute the formulas for the velocities, they are the same as the indefinite integral:
\begin{aligned} & v(t) = \int t^4 \mathrm dt = \frac{t^5}{5} + C_1 \\ & v(t) =\int \cos(t) \mathrm dt = \sin(t) + C_1 \\ & v(t) \int \left( t^2 - 2\right) \mathrm dt = \frac{t^3}{3} -2t + C_1 \end{aligned}
The position is another integration (for the dummy variable s will be used):
\begin{aligned} & x(t) = \int v(t) \mathrm dt = \int \left( \frac{t^5}{5} + C_1 \right) \mathrm dt = \frac{t^6}{30} + C_1 t \\ & x(t) = \int v(t) \mathrm dt = \int \left( \sin(t) + C_1 \right) \mathrm dt = -\cos(t) + C_1 t \\ & x(t) = \int v(t) \mathrm dt = \int \left( \frac{t^3}{3} - 2t + C_1 \right) \mathrm dt = \frac{t^4}{12} - t^2 + C_1 t \end{aligned}
Integrating between 0 and t (for the dummy variable s will be used):
\begin{aligned} & v(t) = \int_0^t s^4 \mathrm ds = \frac{s^5}{5} \bigg|_0^t = \frac{t^5}{5} \\ & v(t) =\int_0^t \cos(s) \mathrm ds = \sin(s) \bigg|_0^t = \sin(t) \\ & v(t) \int_0^t \left( s^2 - 2\right) \mathrm ds = \left[\frac{s^3}{3} -2s \right] \bigg|_0^t = \frac{t^3}{3} -2t \end{aligned}
Finally for the position:
\begin{aligned} & x(t) = \int_0^t v(s) \mathrm ds = \int_0^t \frac{s^5}{5} \mathrm ds = \frac{s^6}{30}\bigg|_0^t = \frac{t^6}{30} \\ & x(t) = \int_0^t v(s) \mathrm ds = \int_0^t \sin(s) \mathrm ds = -\cos(s)\bigg|_0^t = -\cos(t) + 1 \\ & x(t) = \int_0^t v(s) \mathrm ds = \int_0^t \left( \frac{s^3}{3} - 2s \right) \mathrm dt = \left[ \frac{s^4}{12} - s^2 \right]\bigg|_0^t = \frac{t^4}{12} - t^2 \end{aligned}
Exercise I2.4
Finish evaluating:
\int_0^{\frac{\pi}{2}} x\cos(x)\mathrm dx
\begin{aligned} \int_0^{\frac{\pi}{2}} x\cos(x)\mathrm dx = & \frac{\pi}{2}\sin\left(\frac{\pi}{2}\right) - \int_0^{\frac{\pi}{2}} \sin(x)\mathrm dx \\ = & \frac{\pi}{2} + \cos(x)\bigg|_0^{\frac{\pi}{2}} = \frac{\pi}{2} + \cos\left(\frac{\pi}{2}\right) - \cos\left(0\right) = \frac{\pi}{2} - 1 \approx 0.5708 \end{aligned}
Lecture 3
Exercise 3.1
Given a force that varies with time according to F = 2t^2, and with the initial condition at time zero, x(0) = \pi, use Aristotle’s law to find x(t) at all times.
Aristotle’s law in equation form are:
\mathbf F = m\,\mathbf v
It is possible to compare this formulation with the definition of deterministic law of motions. Integrating to get the position:
\mathbf x = \int \mathbf v = \int \frac{\mathrm d r}{\mathrm dt} \mathrm dt = \mathbf r(t) + c = \int \frac{\mathbf F}{m} \mathrm dt
In particular with F(t) = 2t^2 and considering a one dimensional particle:
x(t) = \int \frac{F}{m} \mathrm dt = \frac{2}{3m} t^3 + C
Using the condition x(0) = x_0 = \pi then:
x(0) = C = \pi Finally, at all times:
x(t) = \frac{2}{3m} t^3 + \pi
Exercise 3.2
Integrate this equation. Hint: Use definite integrals.
Starting from Newton’s Law:
\mathbf F = m \, \mathbf a = m \, \frac{ \mathrm d \mathbf v}{\mathrm dt} = m \, \frac{ \mathrm d^2 \mathbf v}{\mathrm dt^2}
Considering F_z constant:
\begin{aligned} & v_z(t) = \int \frac{F_z}{m} \mathrm dt = \frac{F_z}{m} \int \mathrm dt = \frac{F_z}{m} t + C_1 \\ & z(t) = \int v_z \mathrm dt = \frac{F_z}{m} \int t \mathrm dt \int C_0 \mathrm dt = \frac{F_z}{2m}t^2 + C_1t + C_2 \end{aligned}
Then to get the velocity and the position at any time, using the condition at t=0, v_z(0) = v_{z0} and z(0) = z_0:
\begin{aligned} & v_z(0) = \frac{F_z}{m} 0 + C_1 = C_1 = v_{z0} \\ & z(0) = \int v_z \mathrm dt = \frac{F_z}{2m}0 + C_10 + C_2 = z_0 \end{aligned}
giving the equations of motions:
\begin{aligned} & z(t) = \frac{F_z}{2m}t^2 + v_{z0}t + z_0 \\ & v_z(t) = \frac{F_z}{m} t + v_{z0} \\ \end{aligned}
Exercise 3.3
Show by differentiation that this satisfies the equation of motion.
This is the inverse of the previous problem; starting from the equation of motion:
z(t) = \frac{F_z}{2m}t^2 + v_{z0}t + z_0
Taking the first derivative gives v_z:
v_z = \frac{\mathrm dz}{\mathrm dt} = 2\frac{F_z}{2m}t + v_{z0} = \frac{F_z}{m}t + v_{z0}
Taking the second derivatives gives the acceleration a_z:
a_z = \frac{\mathrm dv_z}{\mathrm dt} = \frac{\mathrm d^2z}{\mathrm dt^2} = \frac{F_z}{m}
This is precisely Newton’s law for the z component:
F_z = m\, a_z
Exercise 3.4
Show by differentiation that the general solution to Eq. (6) is given in terms of two constants A and B by
x(t) = A\cos\omega t + B\sin\omega t
Determine the initial position and velocity at time t=0 in terms of A and B.
Starting from the equation, and considering a one dimensional motions (y = v_y = z = v_z = 0) so v \equiv v_x and a \equiv a_x:
\ddot x = -\omega x
and considering the general solution:
x(t) = A\cos(\omega t) + B \sin(\omega t)
Taking the first derivative gives v:
v = \frac{\mathrm dx}{\mathrm dt} = -A\omega sin(\omega t) + B \omega \cos(\omega t)
Taking the second derivatives gives the acceleration a:
a = \frac{\mathrm dv}{\mathrm dt} = \frac{\mathrm d^2x}{\mathrm dt^2} = -A\omega^2 sin(\omega t) - B \omega^2 \cos(\omega t)
Substituting back in the original equation:
\begin{aligned} &\ddot x = a = -\omega^2 x \\ &-A\omega^2 sin(\omega t) - B \omega^2 \cos(\omega t) = -\omega^2 \left(A\cos(\omega t) + B \sin(\omega t) \right) \end{aligned}
which is satisfied.
At t = 0:
\begin{aligned} & x(0) = A\cos(0) + B \sin(0) = A = x_0 \\ & v(0) = -A\omega sin(0) + B \omega \cos(0) = B\omega = v_0 \end{aligned}
So the solution can be written in term of the initial conditions as:
x(t) = x_0\cos(\omega t) + \frac{v_0}{\omega} \sin(\omega t)
Exercise I3.1
Compute all first and second partial derivatives - including mixed derivatives - of the following functions:
$$ \begin{aligned} & x^2+y^2 = \sin(xy) \\ &\frac{x}ye^{\left(x^2+y^2\right)} \\ & e^x\cos y \end{aligned}It won’t be reminder in all the functions, but it is true that:
\frac{\partial^2 f}{\partial x\partial y} = \frac{\partial^2 f}{\partial y\partial x}
f(x,y) = x^2 + y^2 - \sin(xy) = 0
\begin{aligned} & \frac{\partial f}{\partial x} = 2x - y \cos(xy) = 0\\ & \frac{\partial f}{\partial y} = 2y - x \cos(xy) = 0 \\ & \frac{\partial^2 f}{\partial x^2} =2 + y^2 \sin(xy) = 0\\ & \frac{\partial^2 f}{\partial y^2} =2 + x^2 \sin(xy) = 0\\ & \frac{\partial^2 f}{\partial x\partial x} = 2y + xy \sin(xy) - \cos(xy) =0 \end{aligned}
f(x,y) = \tfrac{x}{y} e^{x^2 +y^2}
\begin{aligned} & \frac{\partial f}{\partial x} = \frac{1}{y} e^{x^2 +y^2} + \frac{2x^2}{y} e^{x^2 +y^2} = \frac{1+2x^2}{y} e^{x^2 +y^2} \\ & \frac{\partial f}{\partial y} = -\frac{x}{y^2}e^{x^2 +y^2} + 2x e^{x^2 +y^2} = \left(2x-\frac{x}{y^2}\right)e^{x^2 +y^2} \\ & \frac{\partial^2 f}{\partial x^2} = \frac{4x}{y} e^{x^2 +y^2} + \frac{2x+4x^3}{y} e^{x^2 +y^2} = \frac{6x+4x^3}{y} e^{x^2 +y^2} \\ & \frac{\partial^2 f}{\partial y^2} = 2y\left(2x-\frac{x}{y^2}\right)e^{x^2 +y^2} + \frac{2x}{y^3}e^{x^2 +y^2} = 2x\left(2y-\frac{1}{y}+\frac{1}{y^3} \right) e^{x^2 +y^2} \\ & \frac{\partial^2 f}{\partial x\partial x} = 2x\left(2x-\frac{x}{y^2}\right)e^{x^2 +y^2} + \left(2-\frac{1}{y^2}\right)e^{x^2 +y^2} = \left(4x^2-\frac{2x^2}{y^2}+2-\frac{1}{y^2}\right)e^{x^2 +y^2} \end{aligned}
f(x,y) = e^x\cos(y)
\begin{aligned} & \frac{\partial f}{\partial x} = e^x\cos(y) \\ & \frac{\partial f}{\partial y} = -e^x\sin(y) \\ & \frac{\partial^2 f}{\partial x^2} = e^x\cos(y) \\ & \frac{\partial^2 f}{\partial y^2} = -e^x\cos(y)\\ & \frac{\partial^2 f}{\partial x\partial x} = -e^x\sin(y) \end{aligned}
Exercise I3.2
Consider the points (x=\dfrac\pi2,\,y=-\dfrac\pi2), (x=-\dfrac\pi2,\,y=\dfrac\pi2), (x=-\dfrac\pi2,\,y=-\dfrac\pi2). Are these points stationary points of the following functions? If so, of what type?
\begin{aligned} F(x,y) &&=\quad& \sin x + \sin y \\ G(x,y) &&=\quad& \cos x + \cos y \end{aligned}
Considering the points (x,y):
\begin{aligned} \mathbf A = & \left(\frac{\pi}{2}, -\frac{\pi}{2} \right) \\ \mathbf B = & \left(-\frac{\pi}{2},\frac{\pi}{2} \right) \\ \mathbf C = & \left(-\frac{\pi}{2}, -\frac{\pi}{2} \right) \\ \end{aligned}
The objective is to compute if they are stationary points and of which type.
F(x,y) = \sin(x) + \sin(y)
The first step is to calculate the first derivative to check if the point is stationary.
- \frac{\partial f}{\partial x} = \cos(x)
- \frac{\partial f}{\partial y} = \cos(y)
Putting the previous points expression:
\begin{aligned} & \frac{\partial f}{\partial x}\bigg|_{A_x} = \cos\left(\frac{\pi}{2}\right) = 0, \quad \frac{\partial f}{\partial y}\bigg|_{A_y} = \cos\left(-\frac{\pi}{2}\right) = 0 \\ & \frac{\partial f}{\partial x}\bigg|_{B_x} = \cos\left(-\frac{\pi}{2}\right) = 0, \quad \frac{\partial f}{\partial y}\bigg|_{C_y} = \cos\left(\frac{\pi}{2}\right) = 0 \\ & \frac{\partial f}{\partial x}\bigg|_{C_x} = \cos\left(-\frac{\pi}{2}\right) = 0, \quad \frac{\partial f}{\partial y}\bigg|_{C_y} = \cos\left(-\frac{\pi}{2}\right) = 0 \end{aligned}
For all points the derivative is zero so they are stationary; it is now possible to check the type computing the Hessian.
- \frac{\partial^2 f}{\partial x^2} = -\sin(x)
- \frac{\partial^2 f}{\partial y^2} = -\sin(y)
- \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} = 0
Thus, the Hessian matrix \mathbf H for f(x, y) is:
\mathbf H = \begin{bmatrix} -\sin(x) & 0 \\ 0 & -\sin(y) \end{bmatrix} Computing it for the point \mathbf A:
\mathbf H_A = \begin{bmatrix} -\sin\left(\frac{\pi}{2}\right) & 0 \\ 0 & -\sin\left(-\frac{\pi}{2}\right) \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & +1 \end{bmatrix}
For this matrix, \det(\mathbf H_A) = -1 <0, the point is a saddle.
Computing it for the point \mathbf B:
\mathbf H_B = \begin{bmatrix} -\sin\left(-\frac{\pi}{2}\right) & 0 \\ 0 & -\sin\left(\frac{\pi}{2}\right) \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}
For this matrix, \det(\mathbf H_A) = -1 <0, the point is a saddle.
Computing it for the point \mathbf C:
\mathbf H_C = \begin{bmatrix} -\sin\left(-\frac{\pi}{2}\right) & 0 \\ 0 & -\sin\left(-\frac{\pi}{2}\right) \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}
For this matrix, \det(\mathbf H_A) = 1 > 0, and \operatorname{tr}(\mathbf H_C)=-2, the point is a local maximum.
F(x,y) = \cos(x) + \cos(y)
The first step is to calculate the first derivative to check if the point is stationary.
- \frac{\partial f}{\partial x} = -\sin(x)
- \frac{\partial f}{\partial y} = -\sin(y)
Putting the previous points expression:
\begin{aligned} & \frac{\partial f}{\partial x}\bigg|_{A_x} = -\sin\left(\frac{\pi}{2}\right) = -1, \quad \frac{\partial f}{\partial y}\bigg|_{A_y} = -\sin\left(-\frac{\pi}{2}\right) = 1 \\ & \frac{\partial f}{\partial x}\bigg|_{B_x} = -\sin\left(-\frac{\pi}{2}\right) = 1, \quad \frac{\partial f}{\partial y}\bigg|_{C_y} = -\sin\left(\frac{\pi}{2}\right) = -1 \\ & \frac{\partial f}{\partial x}\bigg|_{C_x} = -\sin\left(-\frac{\pi}{2}\right) = 1, \quad \frac{\partial f}{\partial y}\bigg|_{C_y} = -\sin\left(-\frac{\pi}{2}\right) = 1 \end{aligned}
So neither of these points is stationary.