Chapter 1
Problem 1.1
Considering a room with 14 people with the following age distribution:
| Age | Count |
|---|---|
| 14 | 1 |
| 15 | 1 |
| 16 | 3 |
| 22 | 2 |
| 24 | 2 |
| 25 | 5 |
Selecting one individual from the group, the probability that their age would be 15 is:
P(15) = \frac{N(15)}{14} = \frac{1}{14} \approx 0.0071
The average value is:
\langle j \rangle = \frac{14 + 15 + 16(3) + 22 (2) + 24(2) + 25 (5)}{14} = \frac{294}{14} = 21
\langle j \rangle ^2 is straightforward:
\langle j \rangle ^2 = 21^2 = 441
It is possible to compute \langle j^2 \rangle as:
\begin{aligned} \langle j^2 \rangle & = \sum_{i=1}^n j^2 P(j) = \frac{1}{14}(14^2 + 15^2 + 16^3(3) + 22^2 (2) + 24^2 (2) + 25^2(5)\\ & = \frac{196 + 225 + 256(3) + 484(2) + 576(2) + 625(5)}{14} = \frac{6434}{14} \approx 459.571 \end{aligned}
To compute the standard deviation it is necessary to compute intermediate quantities:
| Age | \Delta j | (\Delta j)^2 | Count |
|---|---|---|---|
| 14 | -7 | 49 | 1 |
| 15 | -6 | 36 | 1 |
| 16 | -5 | 25 | 3 |
| 22 | 1 | 1 | 2 |
| 24 | 3 | 9 | 2 |
| 25 | 4 | 16 | 5 |
Then computing the standard deviation by the definition, starting from the variance:
\sigma^2 = \langle (\Delta j)^2 \rangle = \sum (\Delta j)^2 P(j) = \frac{49 + 36 + 25(3) + 1(2) + 9(2) + 16(5)}{14} = \frac{260}{14} \approx 18.57
and then taking the square root:
\sigma = \sqrt {\sigma^2} \approx \sqrt{18.51} \approx 4.31
It could have been possible to use the shorter formula:
\sigma = \sqrt{\langle j^2 \rangle - \langle j \rangle^2} = \sqrt{\frac{6434}{14} - 441} \approx 4.31
which leads to the same result.
Problem 1.2
Considering an object that is dropped from an height h; while the fall, “many” pictures are taken (considering as if they are so many that is considered continuous).
To compute the average of the distances, the total time need to be computed first; ignoring the air resistance, and apply F = m\ddot x = mg then:
\begin{aligned} & v = \frac{\mathrm dx}{\mathrm dt} = \int \frac{F}{m} \mathrm dt = gt \\ & x = \int gt\, \mathrm dt = \frac{1}{2} gt^2 \end{aligned}
The total flight time is:
T = \sqrt{\frac{2h}{g}}
The probability that a picture was taken between t and t + \mathrm dt is \frac{\mathrm dt}{T}, so the probability that it shows a distance \mathrm dx is:
\frac{\mathrm dt}{T} = \frac{\delta x}{gt}\frac{1}{T} = \frac{\mathrm x}{g}\sqrt{\frac{g}{2x}}\sqrt{\frac{g}{2h}}=\frac{1}{2\sqrt{hx}}\mathrm dx
Therefore the probability density is:
\rho = \frac{1}{2\sqrt{hx}}\mathrm dx, \quad (0 \le x \le h)
It is possible to verify the calculations:
\int_0^h \frac{1}{2\sqrt{hx}}\mathrm dx = \frac{1}{2\sqrt h} \left( 2x^{\frac{1}{2}} \right) \bigg|_0^h = 1
The average distance is:
\langle x \rangle = \int_0^h x \frac{1}{2\sqrt{hx}}\mathrm dx = \frac{1}{2\sqrt h} \left( \frac{2}{3}x^{\frac{3}{2}} \right) \bigg|_0^h = \frac{h}{3}
It is possible to plot the probability density \rho(x).
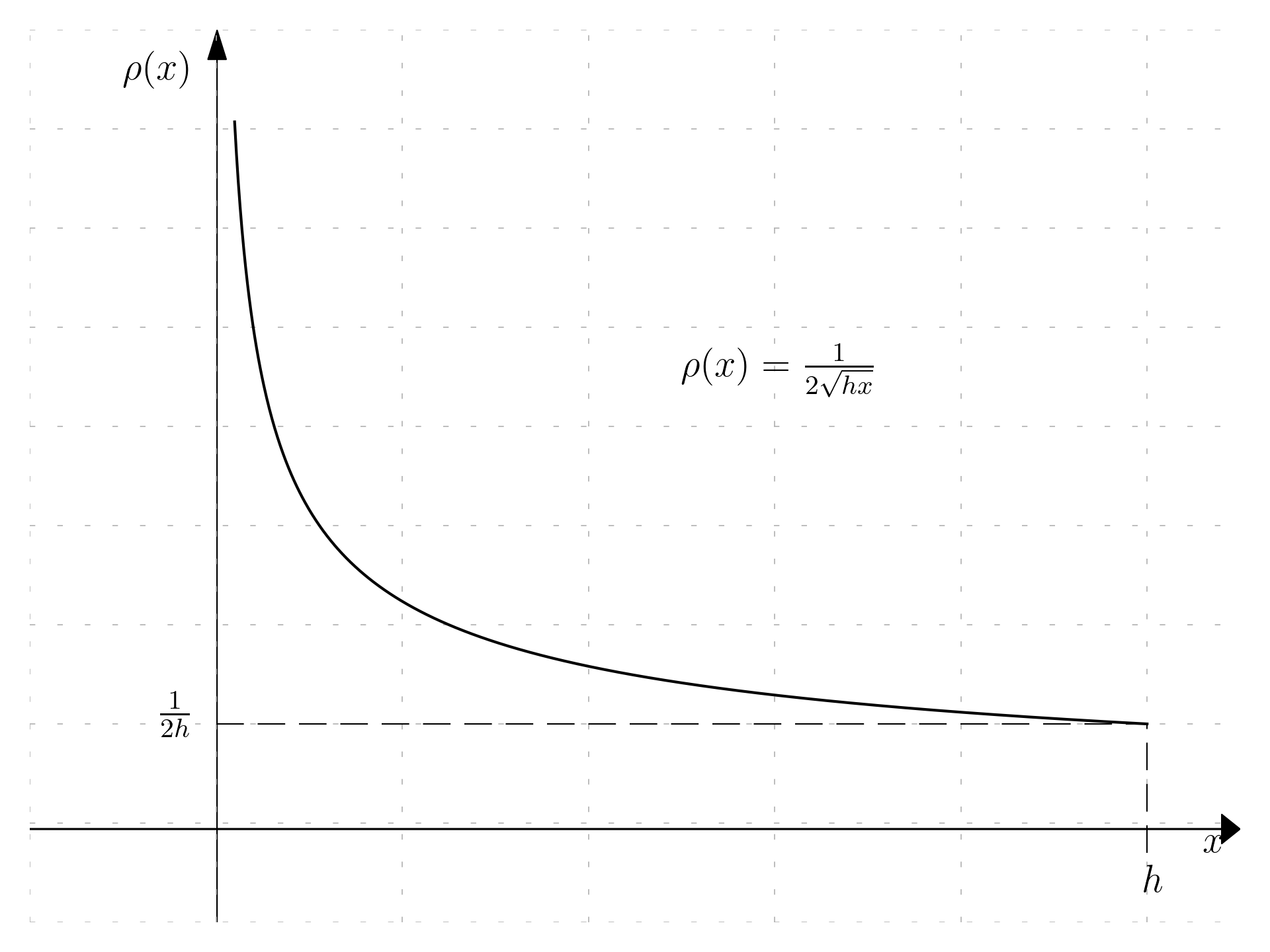
The standard deviation for this distribution can be computed first computing \langle x^2 \rangle:
\langle x^2 \rangle = \int_0^h x^2 \frac{1}{2\sqrt{hx}}\mathrm dx = \frac{1}{2\sqrt h} \left( \frac{2}{5}x^{\frac{5}{2}} \right) \bigg|_0^h = \frac{1}{5}h^2
Then apply the formula for the standard deviation:
\sigma^2 = \langle x^2 \rangle - \langle x \rangle ^2 = \frac{1}{5}h^2 - \frac{1}{9}h^2 = \frac{4}{45}h^2
which gives:
\sigma = \frac{2}{3\sqrt 5}h = 0.2981 h
To complete the example, it is possible to compute the probability that a picture will be at more than one standard deviation from the average.
Starting from a generic interval [a,b]:
P_{ab} = \int_a^b \frac{1}{2\sqrt{hx}}\mathrm dx = \frac{1}{2\sqrt h} \left( 2x^{\frac{1}{2}} \right) \bigg|_a^b = \frac{1}{\sqrt h}\left(\sqrt b - \sqrt a \right)
The probability that the measurement will be outside one standard deviation is:
\begin{aligned} & b = \langle x \rangle + \sigma = 0.333 h + 0.291 h = 0.6315 h \\ & a = \langle x \rangle - \sigma = 0.333 h - 0.291 h = 0.0352 h \\ & P = 1 - P_{ab} = 1 - \frac{1}{\sqrt h}\left(\sqrt b - \sqrt a \right) = 1 - \left( \sqrt{0.6315} - \sqrt{0.0352}\right) = 0.393 \end{aligned}
Problem 1.3
Consider the Gaussian distribution:
\rho(x) = A e^{-\lambda(x-a)^2}, \quad A,a,\lambda \in \mathbb R
The condition that this integral should give 1 impose a condition on A as function of the others quantities:
\int_{-\infty}^\infty A e^{-\lambda(x-a)^2} \mathrm dx = A \int_{-\infty}^\infty e^{-\lambda\,u^2} \mathrm du = A\sqrt{\frac{\pi}{\lambda}} = 1
which gives:
A = \sqrt{\frac{\lambda}{\pi}}
Then it is possible to compute \sigma based on the averages \langle x\rangle and \langle x^2\rangle
\begin{aligned} \langle x \rangle & = \int_{-\infty}^\infty A xe^{-\lambda(x-a)^2} \mathrm dx = \sqrt{\frac{\lambda}{\pi}} \int_{-\infty}^\infty (u+a) e^{-\lambda\,u^2} \mathrm du \\ & = \sqrt{\frac{\lambda}{\pi}} \left( \int_{-\infty}^\infty u e^{-\lambda\,u^2} \mathrm du + \int_{-\infty}^\infty a e^{-\lambda\,u^2} \mathrm du \right) = \sqrt{\frac{\lambda}{\pi}} \left( 0 + a \sqrt{\frac{\pi}{\lambda}} \right) = a \\ \langle x^2 \rangle & = \int_{-\infty}^\infty A x^2 e^{-\lambda(x-a)^2} \mathrm dx = \sqrt{\frac{\lambda}{\pi}} \int_{-\infty}^\infty (u+a)^2 e^{-\lambda\,u^2} \mathrm du \\ & = \sqrt{\frac{\lambda}{\pi}} \left( \int_{-\infty}^\infty u^2 e^{-\lambda\,u^2} \mathrm du + 2a \int_{-\infty}^\infty 2u e^{-\lambda\,u^2} \mathrm du \int_{-\infty}^\infty a^2 e^{-\lambda\,u^2} \mathrm du \right) \\ & = \sqrt{\frac{\lambda}{\pi}} \left( \frac{1}{2\lambda} \sqrt{\frac{\pi}{\lambda}} + 0 + a^2 \sqrt{\frac{\pi}{\lambda}} \right) = \frac{1}{2\lambda} + a^2 \\ \sigma & = \sqrt{\langle x^2 \rangle - \langle x^2 \rangle} = \sqrt{\frac{1}{2\lambda} + a^2 - a^2} = \frac{1}{\sqrt{2\lambda}} \end{aligned}
It is also possible to sketch the graph of \rho(x).
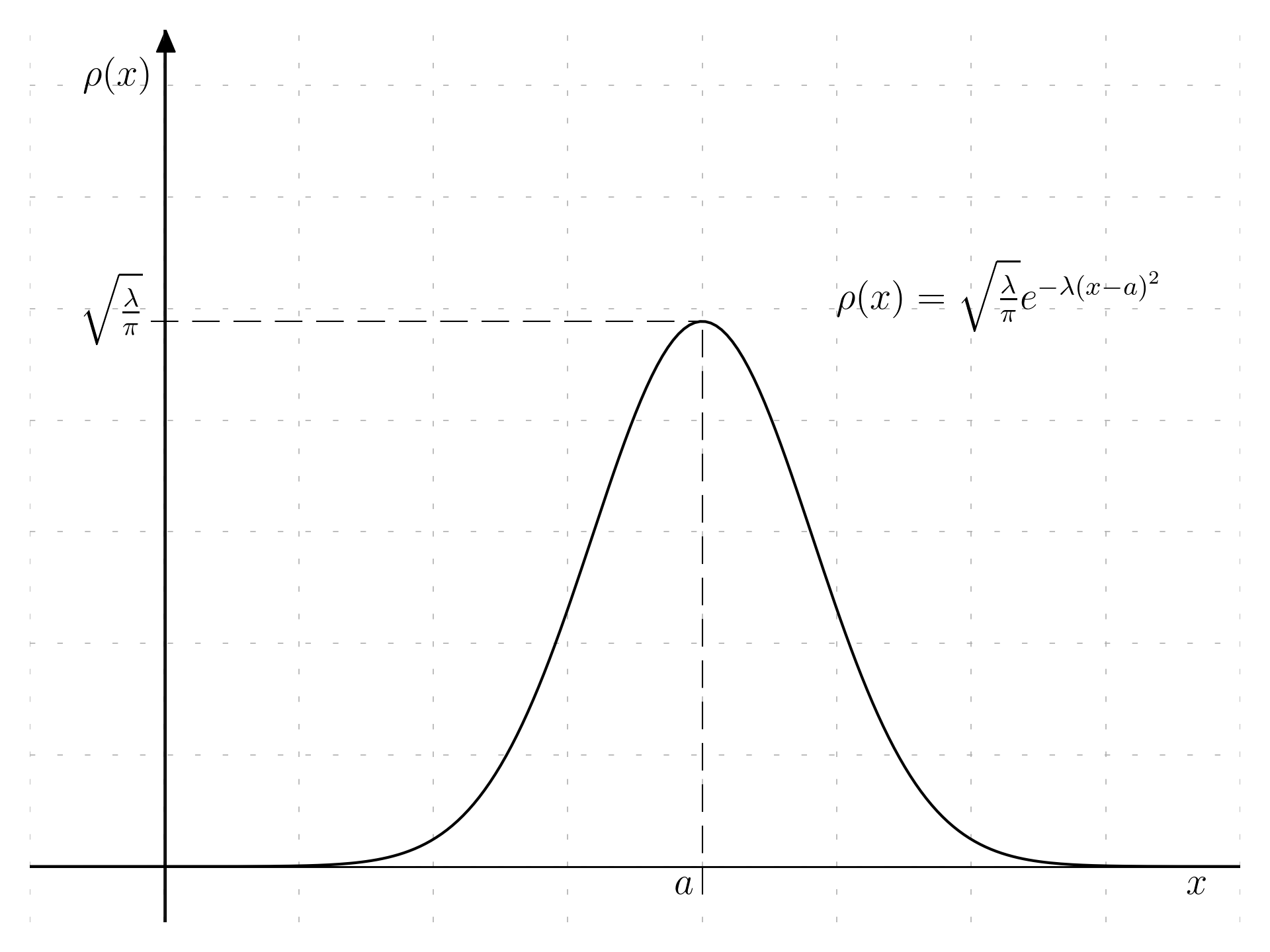
Problem 1.4
At time t=0 a particle is represented by the wave function (with A,a,b \in \mathbb R^+):
\Psi(x,0) = \begin{cases} A\left( \frac{x}{a} \right) & 0 \le x \le a \\ A\left( \frac{b - x}{b - a} \right) & a \le x \le b \\ 0 & x \le 0 \lor x > b \end{cases}
The first step is to normalize \Psi(x,0) (already excluding the part were \Psi = 0):
\begin{aligned} \int_{-\infty}^\infty | \Psi(x,t) |^2 \mathrm dx & = \int_0^a A^2\left( \frac{x^2}{a^2} \right) \mathrm dx + \int_a^b A^2\left( \frac{b - x}{b - a} \right)^2 \mathrm dx = \frac{A^2}{a^2} \frac{x^3}{3}\bigg|_0^a + \frac{A^2}{(b-a)^2}\frac{-(b-x)^3}{3} \bigg|_a^b \\ & = \frac{A^2a}{3} + \frac{A^2(b-a)}{3} = \frac{A^2a}{3} + \frac{A(b-a)}{3} = A^2\left(\frac{a + b -a }{3}\right) = A^2 \frac{b}{3} = 1 \end{aligned}
And therefore:
A = \sqrt{\frac{b}{3}}
With this condition it is then possible to sketch the function:
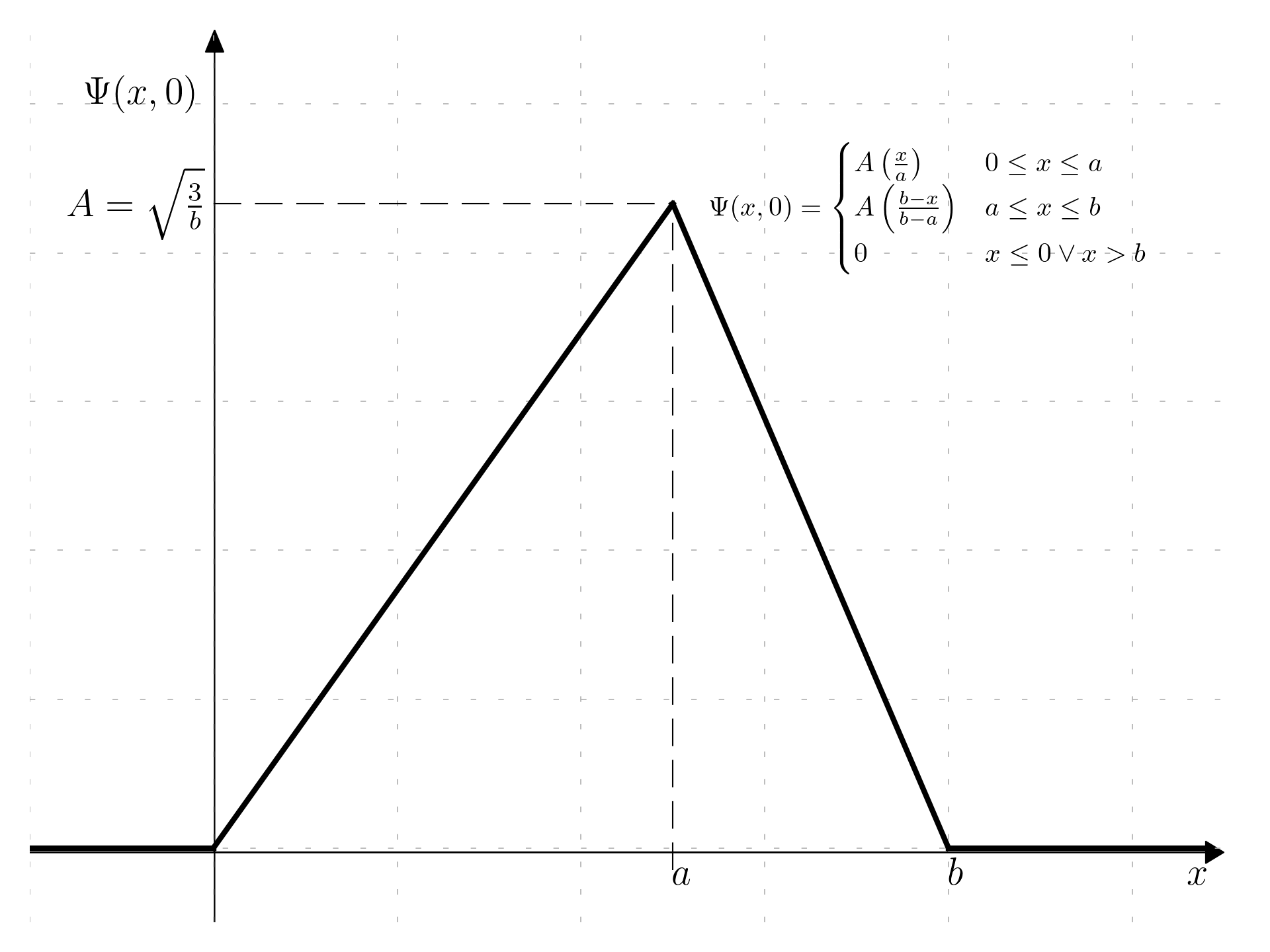
The maximum probability to find the function at t=0 is naturally at the position a.
In particular cases (b=a or b=2a) the probability is analytical (P=1 and P=0.5 respectively) and can be calculated; in general:
P_{-\infty a} = \int_{-\infty}^a | \Psi(x,t) |^2 \mathrm dx = \int_0^a A^2\left( \frac{x^2}{a^2} \right) \mathrm dx = \frac{A^2}{a}{3} = \frac{a}{b}
That verifies that P_{-\infty a} = 1, b = a and P_{-\infty a} = \frac{1}{2}, b = 2a.
Lastly, it is possible to compute the expectation value of x:
\begin{aligned} \langle x \rangle & = \int_{-\infty}^\infty x | \Psi(x,t) |^2 \mathrm dx = \int_0^a A^2\left( \frac{x^3}{a^2} \right) \mathrm dx + \int_a^b A^2 x \left( \frac{b - x}{b - a} \right)^2 \mathrm dx & \\ & = \frac{3}{a^2b} \frac{x^4}{4}\bigg|_0^a + \frac{3}{b(b-a)^2}\left( \frac{x^2b}{2} -\frac{2x^3b}{3} + \frac{x^4}{4} \right) \bigg|_a^b \\ & = \frac{3a^2}{4b} + \frac{3}{b(b-a)^2}\left( \frac{b^3}{2} -\frac{2b^4}{3} + \frac{b^4}{4} - \frac{a^2b}{2} +\frac{2a^3b}{3} - \frac{a^4}{4} \right) \\ & = \frac{3}{4b(b-a)^2} \left[ a^2(b-a)^2 + 2b^3 - \frac{8b^4}{3} + b^4 - 2a^2b + \frac{8}{3}a^3b - a^4 \right] \\ & = \frac{3}{4b(b-a)^2} \left(a^2b- 2^3b +a^4 + 2b^3 - \frac{8b^4}{3} + b^4 - 2a^2b + \frac{8}{3}a^3b - a^4\right) \\ & = \frac{3}{4b(b-a)^2} \left(-a^2b^2 + \frac{b^4}{4} + \frac{2}{3}a^3b \right) = \frac{3}{4b(b-a)^2} \frac{b}{3}\left(b^3 - 3a^2b + 2a^3 \right) \\ & = \frac{1}{(b-a)^2} \left(b^3 - 3a^2b + 2a^3 \right) = \frac{2a + b}{4} \end{aligned}
Problem 1.5
Considering the wave function:
\Psi(x,t) = A e^{-\lambda |x|}e^{-i\omega t}, \quad A, \lambda, \omega \in \mathbb R
The first step is to normalize this function, for example at t=0:
\int_{-\infty}^\infty |\Psi(x,t)|^2 \mathrm dx = \int_{-\infty}^\infty A^2 e^{-2\lambda |x|} \mathrm dx = 2A^2 \int_0^\infty e^{-2\lambda |x|} \mathrm dx = \frac{e^{-2\lambda |x|}}{-2\lambda}\bigg|_0^\infty = \frac{2A^2}{2\lambda} = \frac{A^2}{\lambda} = 1
This gives the constant:
A = \sqrt{\lambda}
Then it is possible to compute \sigma based on the average \langle x\rangle and \langle x^2\rangle:
\begin{aligned} \langle x \rangle & = \int_{-\infty}^\infty A^2 x e^{-2\lambda |x|} \mathrm dx = \lambda \int_{-\infty}^\infty x e^{-2\lambda |x|} \mathrm dx = 0 \\ \langle x^2 \rangle & = \int_{-\infty}^\infty A^2 x^2 e^{-2\lambda |x|} \mathrm dx = 2\lambda \int_{0}^\infty x e^{-2\lambda |x|} \mathrm dx = 2\lambda \frac{2}{(2\lambda^3)} = \frac{1}{2\lambda^2} \\ \sigma & = \sqrt{\langle x^2 \rangle - \langle x^2 \rangle} = \sqrt{\frac{1}{2\lambda^2}} = \frac{1}{\sqrt{2}\lambda} \end{aligned}
It is possible to sketch the function |\Psi(x,0)|^2.
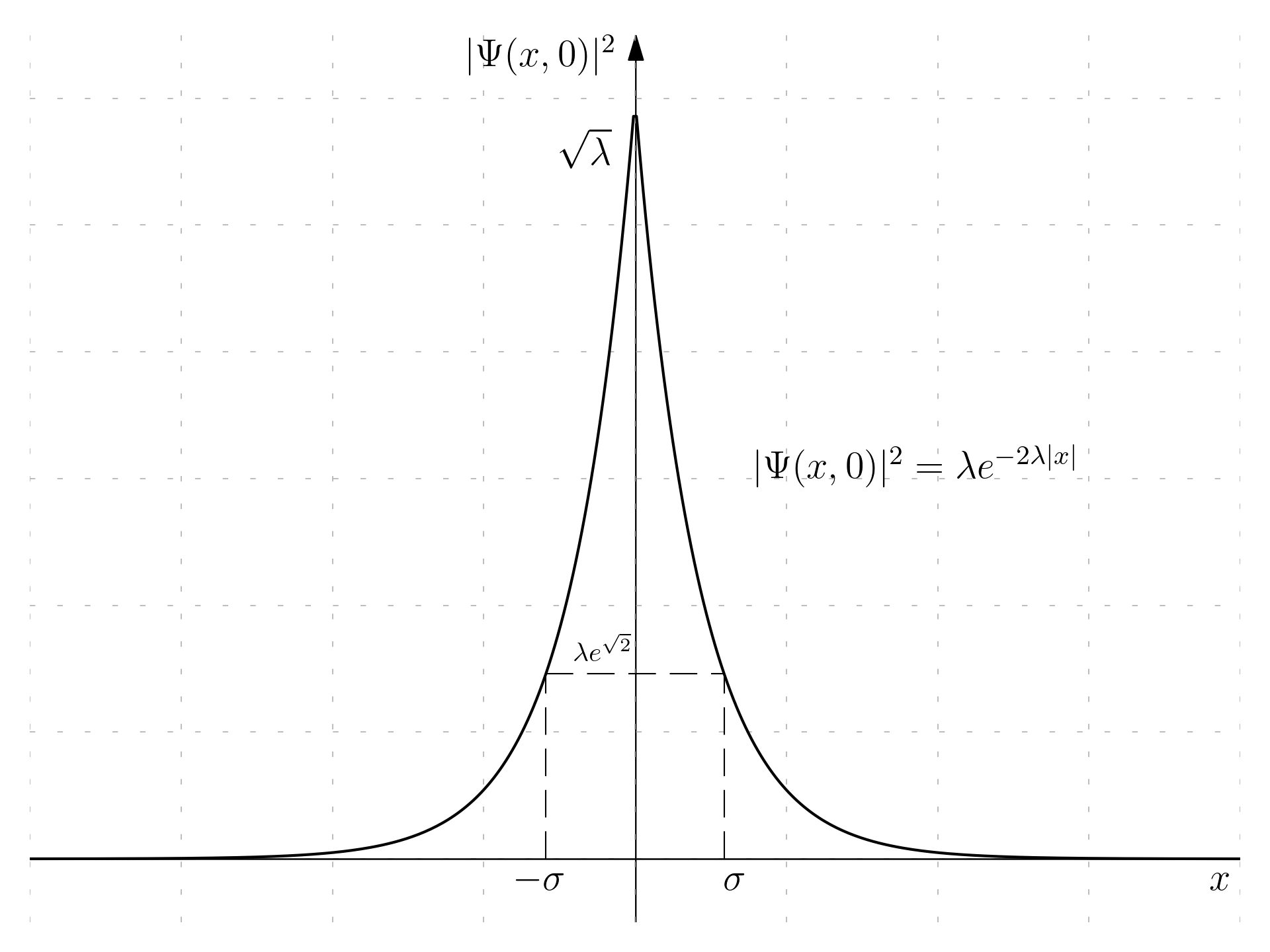
The value at \pm \sigma is:
|\Psi(\sigma,0)|^2 = \lambda^2 e^{-2 \lambda \frac{1}{\sqrt 2 \lambda}} = \lambda e^{-\sqrt 2} = 0.243 \, \lambda
The probability that the value is outside this area is:
2\int_\sigma^\infty |\Psi|^2 \mathrm dx = 2 A^2 \int_\sigma^\infty e^{-2\lambda x} \mathrm dx = 2\lambda \frac{e^{-\lambda x}}{-2\lambda}\bigg|_\sigma ^\infty = e^{-2\lambda \sigma} = e^{-\sqrt 2} = 0.243
Therefore the probability is around 25\%.Problem 1.7
The derivative of the momentum is:
\begin{aligned} \frac{\mathrm d \langle p \rangle }{\mathrm dt} & = -i\hbar \int \frac{\partial}{\partial t} \left(\bar \Psi \frac{\partial \Psi}{\partial x}\right) \mathrm dx = -i\hbar \int \left(\frac{\partial \bar \Psi}{\partial t} \frac{\partial \Psi}{\partial x} + \bar \Psi \frac{\partial}{\partial x} \frac{\partial \Psi}{\partial t} \right) \mathrm dx \\ & =- i\hbar \int \left[ \left( -\frac{\hbar}{2m} \frac{\partial^2 \bar \Psi}{\partial x^2} + \frac{i}{\hbar} V\bar\Psi \right) \frac{\partial \Psi}{\partial x} + \bar \Psi \frac{\partial}{\partial x} \left( \frac{\hbar}{2m} \frac{\partial^2 \Psi}{\partial x^2} - \frac{i}{\hbar} V\Psi \right) \right] \mathrm dx \\ & =- i\hbar \int \left[ \frac{\hbar}{2m} \left(\bar \Psi \frac{\partial^3 \Psi}{\partial x^3} - \frac{\partial^2 \bar \Psi}{\partial x^2} \frac{\partial \Psi}{\partial x} \right) + \frac{i}{\hbar} \left(V\bar\Psi \frac{\partial \Psi}{\partial x} - \bar \Psi \frac{\partial V\Psi}{\partial x} \right) \right] \mathrm dx \end{aligned}
The first term can be integrated by parts twice and will result zero:
\bar \Psi \frac{\partial^3 \Psi}{\partial x^3} - \frac{\partial^2 \bar \Psi}{\partial x^2} \frac{\partial \Psi}{\partial x} = - \frac{\partial \bar \Psi}{\partial x} \frac{\partial^2 \Psi}{\partial x^2} - \frac{\partial^2 \bar \Psi}{\partial x^2} \frac{\partial \Psi}{\partial x} = \frac{\partial^2 \bar \Psi}{\partial x^2} \frac{\partial \Psi}{\partial x} - \frac{\partial^2 \bar \Psi}{\partial x^2} \frac{\partial \Psi}{\partial x} = 0
The second term expanding it:
V\bar\Psi \frac{\partial \Psi}{\partial x} - \bar \Psi \frac{\partial V\Psi}{\partial x} = V\bar\Psi \frac{\partial \Psi}{\partial x} - V \bar \Psi \frac{\partial \Psi}{\partial x} - \Psi \bar \Psi \frac{\partial V}{\partial x} = -|\Psi|^2 \frac{\partial V}{\partial x}
And therefore:
\frac{\mathrm d \langle p \rangle }{\mathrm dt} = - i\hbar \int \frac{i}{\hbar} |\Psi|^2 \frac{\partial V}{\partial x} \mathrm dx = \int |\Psi|^2 \frac{\partial V}{\partial x} \mathrm dx = \big\langle -\frac{\partial V}{\partial x} \big\rangle
This is an instance of Ehrenfest’s Theorem, which assert that expectation values obey the classical laws.
Problem 1.9
Considering the wave function:
\Psi(x,t) = A e^{-a\left[ \left( \frac{mx^2}{\hbar}\right) +it \right]}, \quad A, a \in \mathbb R
The first step is to normalize the function (that will gives A):
\int_{-\infty}^{\infty} \Psi^2 \mathrm dx = \int_{-\infty}^{\infty} A^2 e^{-2a \left( \frac{mx^2}{\hbar}\right)} \mathrm dx = A^2 \sqrt{\frac{\pi\hbar}{2am}}
So:
A = \sqrt[4]{\left(\frac{2am}{\pi\hbar}\right)}
It is possible to find for which potential energy function V(x) it is a solution of the Schrödinger equation:
i\hbar \frac{\partial \Psi}{\partial t} = -\frac{\hbar^2}{2m} \frac{\partial^2 \Psi}{\partial x^2} + V\Psi
Computing the derivatives:
\begin{aligned} \frac{\partial \Psi}{\partial t} & = -ia A e^{-a\left[ \left( \frac{mx^2}{\hbar}\right) +it \right]} = -ia \Psi \\ \frac{\partial^2 \Psi}{\partial x^2} & = \frac{\partial}{\partial x}\left(A \frac{-am}{\hbar} e^{-a\left[ \left( \frac{mx^2}{\hbar}\right) +it \right]} 2x \right) = - \frac{2Aam}{\hbar} e^{-a\left[ \left( \frac{mx^2}{\hbar}\right) +it \right]} + A \frac{a^2m^2}{\hbar^2} e^{-a\left[ \left( \frac{mx^2}{\hbar}\right) +it \right]} 4x^2 \\ & = -\frac{2am}{\hbar}\Psi + \frac{4a^2m^2}{\hbar^2}x^2\Psi = -\frac{2am}{\hbar}\left( 1 -\frac{2amx^2}{\hbar} \right) \Psi \end{aligned}
Substituting them in the equation :
i\hbar \left( -ia \Psi \right) = -\frac{\hbar^2}{2m} \left[-\frac{2am}{\hbar}\left( 1 -\frac{2amx^2}{\hbar} \right)\right]\Psi + V\Psi
\Psi can be factorized since is not zero, and the remaining is a function of x and V only:
-1\times-a\hbar = a \hbar \left(1-\frac{2amx^2}{\hbar}\right) + V
expanding:
V = a\hbar -a\hbar + 2a^2 x^2 = 2a^2 x^2
Then it is possible to compute \sigma_x based on the average \langle x\rangle and \langle x^2\rangle:
\begin{aligned} \langle x \rangle & = \int_{-\infty}^{\infty} A^2 x e^{-2a \left( \frac{mx^2}{\hbar}\right)} \mathrm dx = 0 \\ \langle x^2 \rangle & = \int_{-\infty}^{\infty} A^2 x^2 e^{-2a \left( \frac{mx^2}{\hbar}\right)} \mathrm dx = A^2 \frac{\sqrt \pi}{2}\left(\frac{\hbar}{2am}\right)^{\frac{3}{2}} = \sqrt{\left(\frac{2am}{\pi\hbar}\right)}\frac{\sqrt \pi}{2}\left(\frac{\hbar}{2am}\right)^{\frac{3}{2}} = \frac{\hbar}{4am} \\ \sigma_x & = \sqrt{\langle x^2 \rangle - \langle x^2 \rangle} = \sqrt {\frac{\hbar}{4am}} \end{aligned}
Likewise it is possible to compute \sigma_p based on the average \langle p\rangle and \langle p^2\rangle:
\begin{aligned} \langle p \rangle & = \frac{\mathrm d \langle x \rangle}{\mathrm dx} = 0\\ \langle p^2 \rangle & = \int \bar \Psi \left(\frac{\hbar}{i} \frac{\partial}{\partial x} \right)^2 \Psi \mathrm dx = -\hbar^2 \int \bar \Psi \frac{\partial^2 \Psi}{\partial x^2}\mathrm dx = -\hbar^2 \int \bar \Psi \left[ -\frac{2am}{\hbar}\left( 1 -\frac{2amx^2}{\hbar} \right) \Psi \right] \mathrm dx \\ & = -\hbar^2\left(-\frac{2am}{\hbar}\right) \left[ \int \bar \Psi \Psi \mathrm dx - \int \bar \Psi\frac{2amx^2}{\hbar} \Psi \mathrm dx \right] = 2am\hbar \left( \int |\Psi|^2 \mathrm dx - \frac{2am}{\hbar} \int x^2|\Psi|^2 \mathrm dx \right)\\ & = 2am\hbar \left( 1 - \frac{2am}{\hbar} \langle x^2 \rangle \right) = 2am\hbar \left( 1 - \frac{2am}{\hbar} \frac{\hbar}{4am} \right) = 2am\hbar \left( \frac{1}{2} \right) = am\hbar \\ \sigma_p & = \sqrt{\langle p^2 \rangle - \langle p^2 \rangle} = \sqrt {am\hbar} \end{aligned}
Finally, it can be verified that these quantities are consistent with the uncertainty principle:
\sigma_x\sigma_p = \sqrt {\frac{\hbar}{4am}}\sqrt {am\hbar} = \frac{\hbar}{2}
So they are precisely in line with the principle.
Problem 1.10
Let’s consider the first 25 digits in the expansion of \pi:
\pi = 3.141592653589793238462643
The probability of each digits are \frac{N_j}{N} = \frac{N_j}{25}:
\begin{aligned} & P_0 = \frac{0}{25} = 0\% \quad & P_1 = \frac{2}{25} = 8\% \quad & P_2 = \frac{3}{25} = 12\% \quad & P_3 = \frac{5}{25} = 20\% \quad & P_4 = \frac{3}{25} = 12\% \\[12pt] & P_5 = \frac{3}{25} = 12\% \quad & P_6 = \frac{3}{25} = 12\% \quad & P_7 = \frac{1}{25} = 4\% \quad & P_8 = \frac{2}{25} = 8\% \quad & P_9 = \frac{3}{25} = 12\% \end{aligned}
The most probable digit is 3, for the median 13 digits are \le 4 and 12 are > 5 so the median is 4.
The average is:
\langle j \rangle = \frac{1}{25}\left(2 \times 1 + 3 \times 2 + 5 \times 3 + 3 \times 4 + 3 \times 5 + 3 \times 6 + 1 \times 7 + 2 \times 8 + 3 \times 9 \right) = \frac{118}{25} = 4.72
To compute the standard deviation is necessary to compute \langle j^2 \rangle:
\langle j^2 \rangle = \frac{1}{25}\left(2 \times 1^2 + 3 \times 2^2 + 5 \times 3^2 + 3 \times 4^2 + 3 \times 5^2 + 3 \times 6^2 + 1 \times 7^2 + 2 \times 8^2 + 3 \times 9^2 \right) = \frac{710}{25} = 28.4
Therefore:
\sigma^2 = \langle j^2 \rangle - \langle j \rangle^2 = 2.84 - 4.72^2 = 6.1216
Finally the standard deviation is \sigma = \sqrt {6.1216} \approx 2.4741.
Problem 1.11
Considering a particle of mass m and energy E in a potential well V(x), sliding frictionlessly back and forth between the classical turning point a and b.
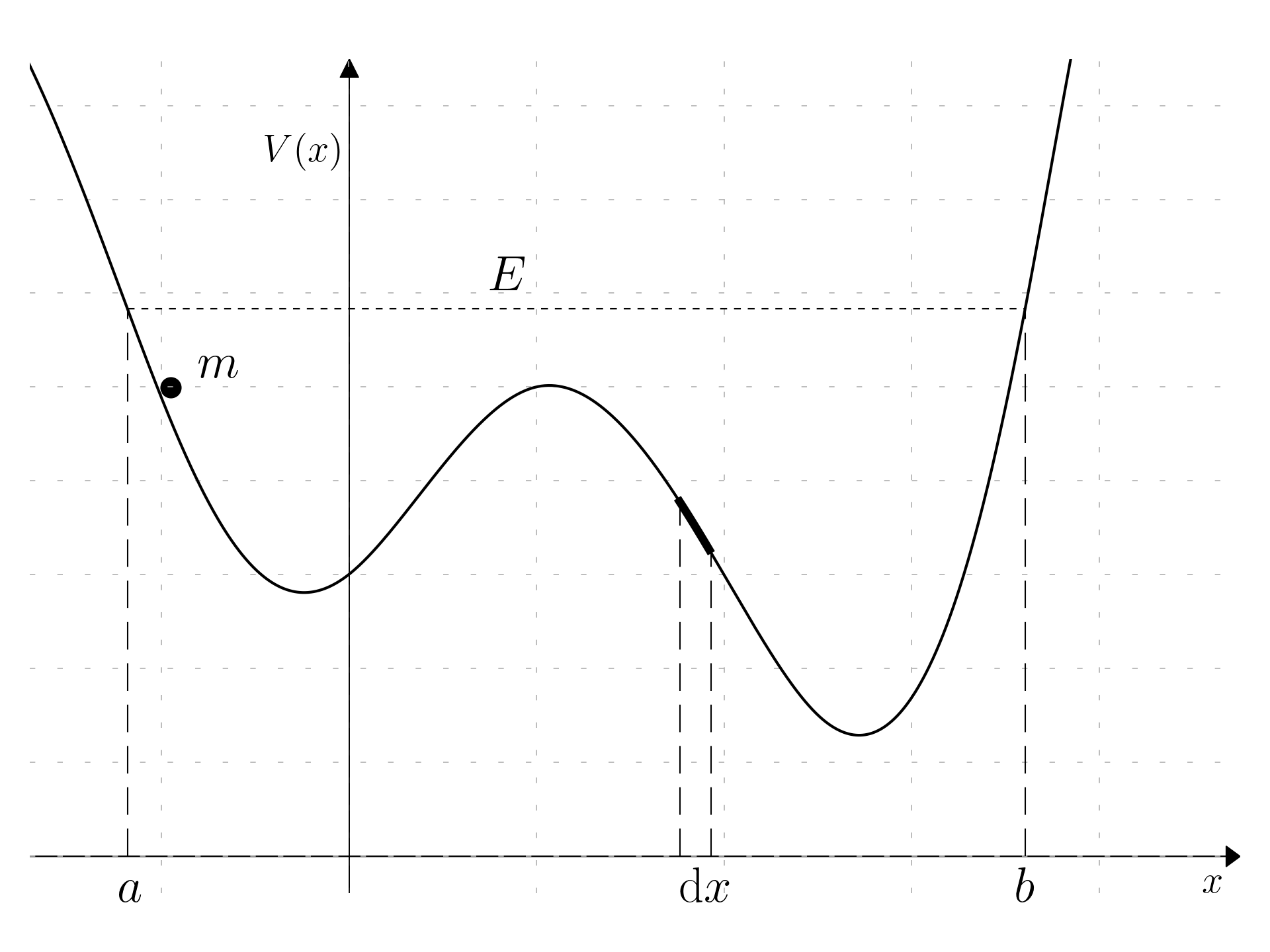
In a classical sense, the probability of finding the particle in the range \mathrm dx is equal to the fraction of time T it takes to get from a to b that it spends in the interval \mathrm dx:
\rho(x)\mathrm dx = \frac{\mathrm dt}{T} = \frac{\frac{\mathrm dt}{\mathrm dx}}{T} \mathrm dx = \frac{1}{v(x)T}\mathrm dx
where:
T = \int_0^T \mathrm dt = \int_a^b \frac{1}{v(x)}\mathrm dx
This is the closest classical analog to |\Psi|^2.
Since the energy is conserved, it is possible to express v(x) as function of it and the potential energy V(x):
E = \frac{1}{2}mv(x)^2 + V(x) \quad \Rightarrow \quad v(x) = \sqrt{\frac{2E-V(x)}{m}}
Considering as example the simple harmonic oscillator, for which:
V(x) = \frac{kx^2}{2}
As the energy is constant and at the points a and b, v(x)=0:
E = \frac{kb^2}{2} = \frac{ka^2}{2}
that implies that:
a = -b
and the velocity can be written as:
v(x) = \sqrt{\frac{k}{m}\left(b^2 - x^2\right)}
Calculating T:
\begin{aligned} T & = \int_a^b \frac{1}{v(x)}\mathrm dx = \sqrt{\frac{k}{m}}\int_{-b}^b \frac{1}{\sqrt{b^2 - x^2}} \mathrm dx = 2\sqrt{\frac{k}{m}}\int_0^b \frac{1}{\sqrt{b^2 - x^2}} \mathrm dx \\ & = 2 \sqrt{\frac{k}{m}} \arctan \left({\frac{x}{\sqrt{b^2 - x^2}}}\right) \bigg|_0^b = 2 \sqrt{\frac{k}{m}} \left[\lim_{x\to b}\arctan \left(\frac{x}{\sqrt{b^2 - x^2}}\right) - \arctan (0) \right] = 2\sqrt{\frac{k}{m}}\frac{\pi}{2} = \sqrt{\frac{k}{m}}\pi \end{aligned}
The distribution is then:
\rho(x) = \frac{1}{v(x)T} = \frac{1}{\sqrt{\frac{k}{m}\left(b^2 - x^2\right)}\sqrt{\frac{k}{m}}\pi} = \frac{1}{\pi \sqrt{b^2 - x^2}}
Checking on the normalization and using the previously computed integral:
\int_{-b}^b \rho(x) \mathrm dx = \frac{2}{\pi}\int_0^b \frac{1}{\sqrt{b^2 - x^2}} \mathrm dx = \frac{2}{\pi}\frac{\pi}{2} = 1
so it is properly normalized.
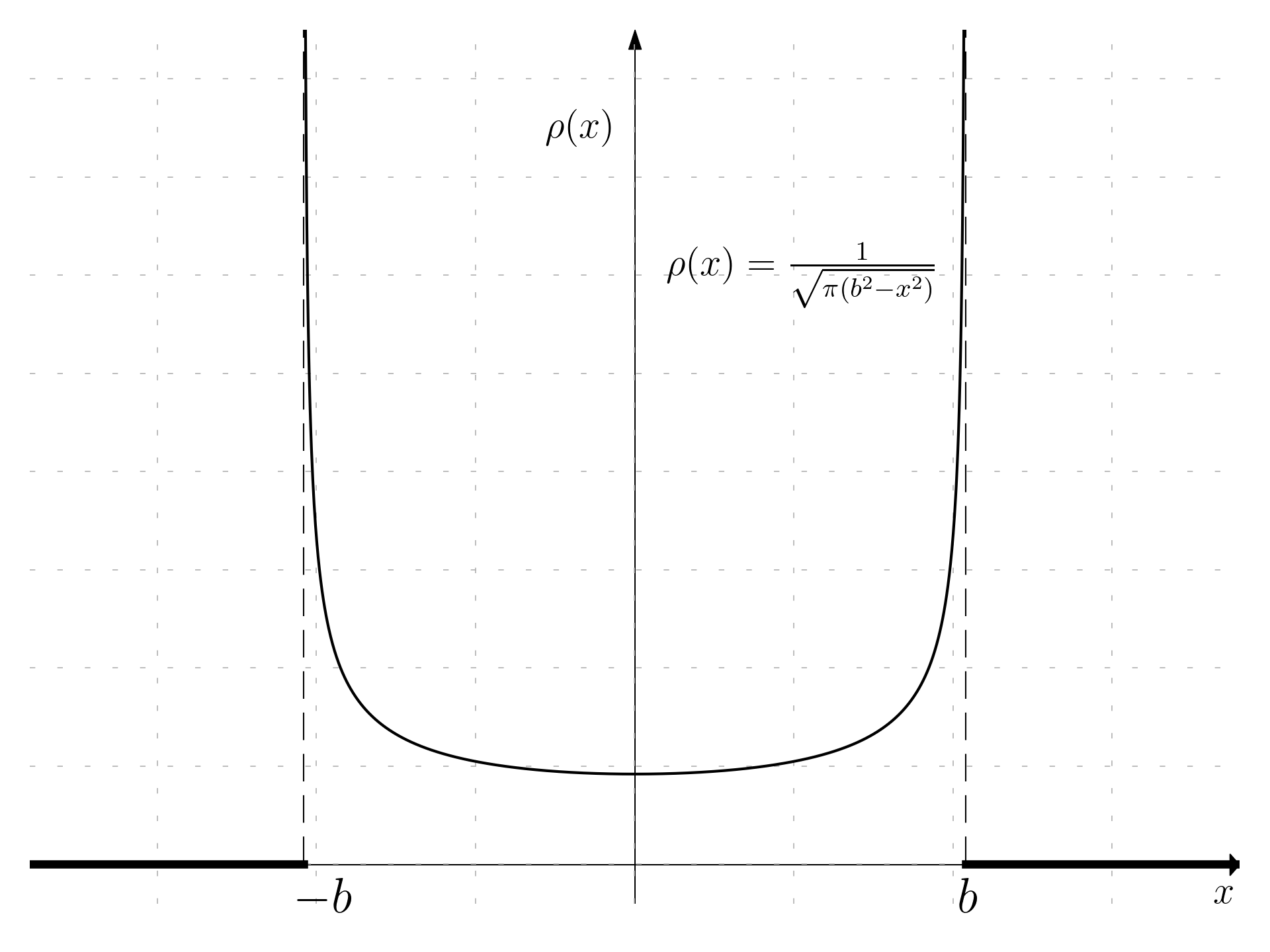
Then it is possible to compute \sigma_x based on the average \langle x\rangle and \langle x^2\rangle; since the function is odd:
\langle x \rangle = \int_{-b}^b x\rho(x)\mathrm dx = \frac{x}{\sqrt{b^2 - x^2}} \mathrm dx = 0
then:
\begin{aligned} \langle x^2 \rangle & = \int_{-b}^b x^2\rho(x)\mathrm dx = \frac{1}{\pi} \int_{-b}^b \frac{x^2}{\sqrt{b^2 - x^2}} \mathrm dx = \frac{2}{\pi} \int_0^b \frac{x^2}{\sqrt{b^2 - x^2}} \mathrm dx \\ & = \frac{2}{\pi} \left[\frac{1}{2}b^2 \arctan\left(\frac{x}{\sqrt{b^2-x^2}}\right) - \frac{1}{2} x \sqrt{b^2-x^2}\bigg|_0^b \right]= \frac{2b^2\pi}{4\pi} =\frac{b^2}{2} = \frac{E}{k} \end{aligned}
Finally:
\sigma_x = \sqrt{\langle x^2 \rangle - \langle x \rangle^2} = \frac{b}{\sqrt 2} = \sqrt{\frac{E}{k}}
Problem 1.12
In a similar way as is possible to compute the standard deviation of the momentum (p =mv).
\rho(p)\mathrm dp = \frac{\mathrm dt}{T} = \frac{\left|\frac{\mathrm dt}{\mathrm dp}\right|\mathrm dp}{T}
\mathrm dt > 0 , but
\frac{\mathrm dp}{\mathrm dt} = F = -kx
From the energy equation, it is possible to express x as a function of p:
E = \frac{p^2}{2m} + \frac{kx^2}{2} \quad \Rightarrow \quad x = \sqrt{\frac{2}{k}\left(E -\frac{p^2}{2m}\right)}
Then it is possible to find \rho(p):
\rho(x) = \frac{1}{kxT} = \frac{1}{\pi k\sqrt{\frac{k}{m}} x} = \frac{1}{\pi k\sqrt{\frac{k}{m}} \frac{2}{k}\left(E -\frac{p^2}{2m}\right)} = \frac{1}{\sqrt{2mE-p^2}} = \frac{1}{\sqrt{c^2-p^2}}
with c \equiv \sqrt{2mE}, which lead to the same expression as \rho(x) with the substitution b \to c; Therefore:
\begin{aligned} & \langle p \rangle = 0 \\ & \langle p^2 \rangle = \frac{c^2}{2} = mE \\ & \langle \sigma_p \rangle = \frac{c}{\sqrt 2} = \sqrt{mE} \end{aligned}
The product \sigma_x \sigma_p is:
\sigma_x \sigma_p = \sqrt{\frac{E}{k}}\sqrt{mE}= E\sqrt{\frac{m}{k}}
This quantity in theory can make as small as possible in the classical sense simply sending E \to 0; in quantum mechanics, an harmonic oscillator energy cannot be less than \frac{\hbar}{2}\omega = \frac{\hbar}{2}\sqrt{\frac{k}{m}}; then:
\sigma_x \sigma_p = E\sqrt{\frac{m}{k}} \ge \frac{\hbar}{2}\sqrt{\frac{k}{m}} \sqrt{\frac{m}{k}}\frac{\hbar}{2} \ge \frac{\hbar}{2}
which express the Heisenberg uncertainty principle.
Problem 1.13
It is possible to check the results with a numerical experiment; the position of the oscillator at time t is given by:
x(t) = A \cos(\omega t)
Setting A = \omega = 1 it is possible to select a certain number of random times, and make a plot of x comparing it with \rho(x), showing that the results match.
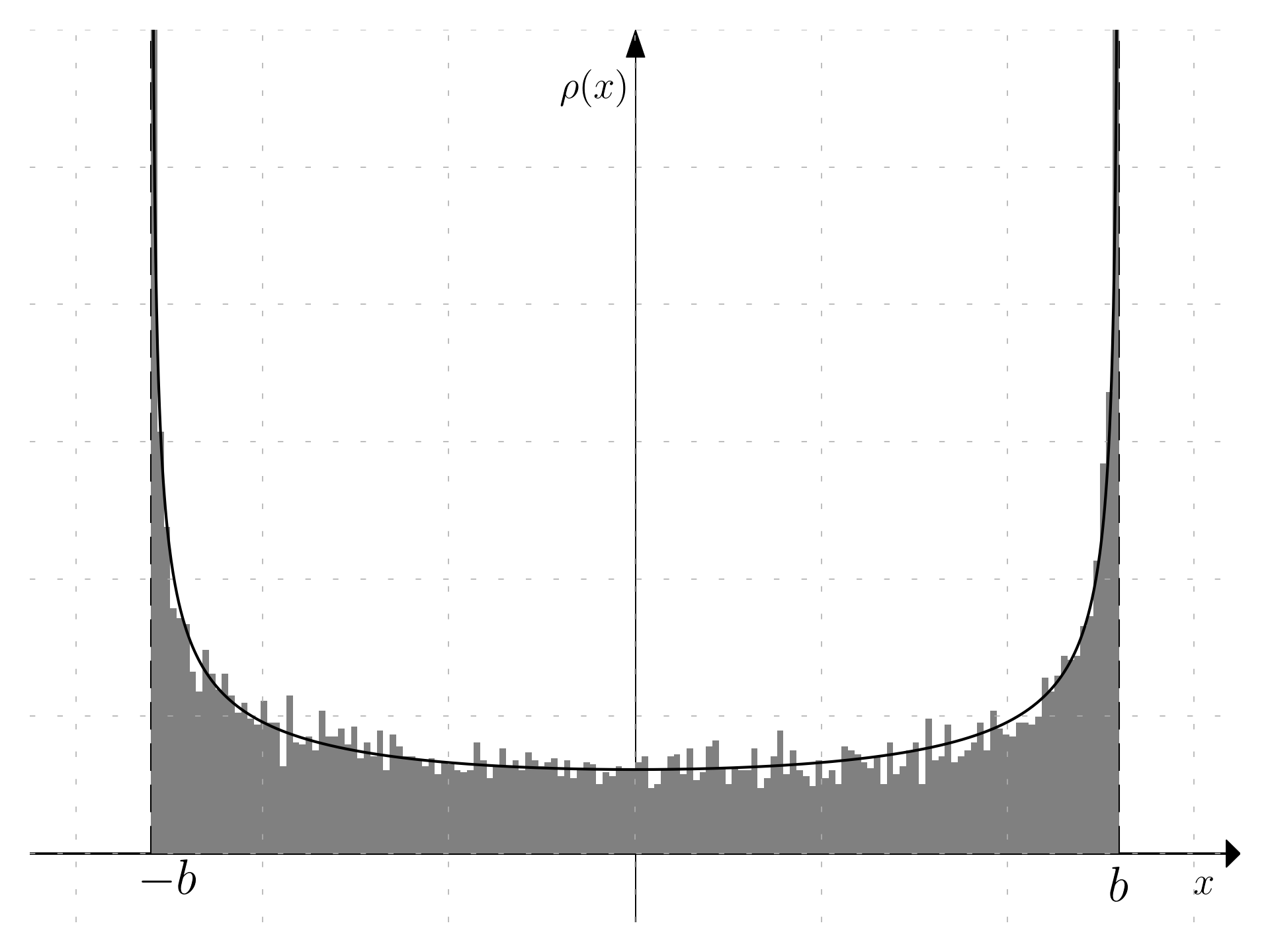
A video with 100,000 random samples showing the convergence to the exact solution is shown below:
Problem 1.14
Let P_{ab} the probability to find the particle in the range (a,b) at time t. The probability current J is defined as:
J(x,t) \equiv \frac{i\hbar}{2m}\left( \Psi \frac{\partial \bar \Psi}{\partial x} - \frac{\partial \bar \Psi}{\partial x} \bar \Psi \right)
Computing the derivative with respect of t of P_{ab}, as
\frac{\partial}{\partial t}|\Psi|^2 = \frac{i\hbar}{2m} \left( \bar \Psi \frac{\partial^2 \Psi}{\partial x^2} - \frac{\partial^2 \bar \Psi}{\partial x^2} \Psi \right) = \frac{\partial}{\partial x} \left[ \frac{i\hbar}{2m} \left( \bar \Psi \frac{\partial \Psi}{\partial x} - \frac{\partial \bar \Psi}{\partial x} \Psi \right) \right] = -\frac{\partial}{\partial x} J(x,t)
it gives immediately:
\begin{aligned} \frac{\mathrm dP_{ab}}{\mathrm dt} & = \frac{\mathrm d}{\mathrm dt}\int_a^b |\psi|^2 \mathrm dx = \int_a^b \frac{\mathrm d|\Psi|^2}{\mathrm dt}\mathrm dx = \int_a^b \frac{\partial}{\partial x} \left[ \frac{i\hbar}{2m} \left( \bar \Psi \frac{\partial \Psi}{\partial x} - \frac{\partial \bar \Psi}{\partial x} \Psi \right) \right] \mathrm dx \\ & = \int_a^b \frac{\partial}{\partial x} J(x,t)\mathrm dx = -J(x,t)\bigg|_a^b = J(a,t) - J(b,t) \end{aligned}
Problem 1.15
Compute:
\frac{\mathrm d}{\mathrm dt}\int_{-\infty}^\infty \bar\Psi_1 \Psi_2 \mathrm dx
for two functions \Psi_1,\Psi_2 which solves the Schrödinger equation with the same potential V(x).
\begin{aligned} \frac{\mathrm d}{\mathrm dt}\int_{-\infty}^\infty \bar\Psi_1 \Psi_2 \mathrm dx & = \int_{-\infty}^\infty \frac{\mathrm d \bar\Psi_1 \Psi_2}{\mathrm dt} \mathrm dx = \int_{-\infty}^\infty \left(\frac{\mathrm d\bar\Psi_1}{\mathrm dt} \Psi_2 + \bar\Psi_1 \frac{\mathrm d\Psi_2}{\mathrm dt} \right)\mathrm dx \\ & = \int_{-\infty}^\infty \left[\left(-\frac{\hbar}{2m} \frac{\partial^2 \bar \Psi_1}{\partial x^2} + \frac{i}{\hbar} V\bar\Psi_1\right)\Psi_2 + \bar\Psi_1 \left(\frac{\hbar}{2m} \frac{\partial^2 \Psi_2}{\partial x^2} - \bar \Psi_1 \frac{i}{\hbar} V\Psi_2\right) \right]\mathrm dx \\ & -\frac{\hbar}{2m} \int_{-\infty}^\infty \left( \frac{\partial^2 \bar \Psi_1}{\partial x^2} \Psi_2 - \frac{\partial^2 \Psi_2}{\partial x^2} \right)\mathrm dx \\ & -\frac{\hbar}{2m}\left[ \frac{\partial \bar \Psi_1}{\partial x}\Psi_2\bigg|_{-\infty}^\infty +\bar \Psi_1 \frac{\partial \bar \Psi_2}{\partial x}\bigg|_{-\infty}^\infty + \int_{-\infty}^\infty \left( -\frac{\partial \bar \Psi_1}{\partial x} \frac{\partial \Psi_2}{\partial x} + \frac{\partial \bar \Psi_1}{\partial x}\frac{\partial \Psi_2}{\partial x} \right)\mathrm dx \right] = 0 \end{aligned}
Problem 1.16
Considering the wave function:
\Psi(x,0)\begin{cases} A\left(a^2 - x^2\right) & \quad -a \le x \le a \\ 0 & \quad x < -a, x>a\end{cases}
Starting from normalizing:
\begin{aligned} \int_{-\infty}^\infty | \Psi(x,t) |^2 \mathrm dx & = \int_{-a}^a A^2\left( a^2 -x^2 \right)^2 \mathrm dx = 2A^2 \int_{0}^a \left( a^2 -x^2 \right)^2 \mathrm dx\\ & = 2A^2 \int_{0}^a \left( a^4 -2a^2x^2 + x^2 \right) \mathrm dx =2A^2 \left( a^4x - \frac{2}{3}a^2x^3 + \frac{1}{5}x^5\bigg|_0^a \right) \\ & = 2A^2 \left( a^5 - \frac{2}{3}a^5 + \frac{1}{5}a^5\right) = \frac{16}{15}a^5A^2 = 1 \end{aligned}
Therefore:
A = \sqrt{\frac{15}{16a^5}}
Then it is possible to compute \sigma based on the averages \langle x\rangle and \langle x^2\rangle.
Starting from \langle x\rangle:
\int_{-\infty}^\infty x| \Psi(x,t) |^2 \mathrm dx = \int_{-a}^a x A^2\left( a^2 -x^2 \right)^2 \mathrm dx = 0
This integral is zero because the integrand is an odd function; then \langle x^2 \rangle:
\begin{aligned} \langle x^2 \rangle & = \int_{-\infty}^\infty x^2| \Psi(x,t) |^2 \mathrm dx = \int_{-a}^a x^2 A^2\left( a^2 -x^2 \right)^2 \mathrm dx \\ & = 2A^2 \int_{0}^a \left( a^4x^2 -2a^2x^4 + x^6 \right) \mathrm dx =2A^2 \left( \frac{a^4}{3}x^3 - \frac{2}{5}a^2x^5 + \frac{1}{7}x^7\bigg|_0^a \right) \\ & = 2A^2 \left( a^7 - \frac{2}{5}a^7 + \frac{1}{7}a^7\right) = \frac{16}{105}a^7A^2 =\frac{16}{105}a^7\frac{15}{16a^5} = \frac{a^2}{7} \end{aligned}
Therefore the standard deviation \sigma_x is:
\sigma_x = \sqrt{\langle x^2 \rangle - \langle x \rangle^2} = \frac{a}{\sqrt 7}
Computing the momentum \langle p \rangle:
\begin{aligned} \langle p \rangle & = \int_{-\infty}^\infty \bar \Psi(x,t)\left(-i\hbar\frac{\partial}{\partial x}\right) \Psi(x,t) \mathrm dx= -i\hbar\int_{-a}^a A\left( a^2 -x^2 \right) \frac{\partial}{\partial x}\left[A\left (a^2 -x^2 \right)\right] \mathrm dx \\ & = A^2ih\int_{-a}^a \left( a^2 -x^2 \right) 2x \mathrm dx = 0 \end{aligned}
This integral is zero because the integrand is an odd function; then \langle p^2 \rangle:
\begin{aligned} \langle p^2 \rangle & = \int_{-\infty}^\infty \bar \Psi(x,t)\left(\hbar^2\frac{\partial^2}{\partial x^2}\right) \Psi(x,t) \mathrm dx= \hbar^2\int_{-a}^a A\left( a^2 -x^2 \right) \frac{\partial^2}{\partial x^2}\left[A\left (a^2 -x^2 \right)\right] \mathrm dx \\ & = 2\hbar^2 A^2\int_{-a}^a \left( a^2 -x^2 \right) \mathrm dx = 4\hbar^2 A^2\left(a^2 x -\frac{x^3}{3}\bigg|_0^a\right) = 4\hbar^2\frac{2}{3}a^3A^2 = \hbar^2\frac{8}{3}a^3\frac{15}{16a^5} = \frac{5\hbar^2}{2a^2} \end{aligned}
Therefore the standard deviation \sigma_p is:
\sigma_p = \sqrt{\langle p^2 \rangle - \langle p \rangle^2} = \frac{\hbar}{a}\sqrt{\frac{5}{2}}
The uncertainty is:
\sigma_x \sigma_p = \frac{a}{\sqrt 7} \frac{\hbar}{a}\sqrt{\frac{5}{2}} = \hbar\sqrt{\frac{5}{14}} \approx .597614304 \times \hbar > \frac{\hbar}{2}
Problem 1.17
Let’s suppose that the objective is to describe an unstable particle that disintegrate with a lifetime \tau; then the probability is not constant but should decrease (for example) with an exponential rate:
P(t) \equiv \int_{-\infty}^\infty | \Psi(x,t) |^2 \mathrm dx = e^{-\frac{t}{\tau}}
One way to achieve this result, it is possible to assume that the potential energy V is no just real (which leads to the conservation of probabilities), but a function as:
V \equiv V_0 -i\Gamma
Then using the Schrödinger equation:
\frac{\partial \Psi}{\partial t} = \frac{\hbar}{2m} \frac{\partial^2 \Psi}{\partial x^2} - \frac{i}{\hbar} \left(V_0 - i\Gamma\right)\Psi
Taking the complex conjugate:
\frac{\partial \bar \Psi}{\partial t} = -\frac{\hbar}{2m} \frac{\partial^2 \bar \Psi}{\partial x^2} + \frac{i}{\hbar} \left(V_0 + i\Gamma\right)\bar\Psi
Therefore:
\frac{\partial}{\partial t}|\Psi|^2 = \frac{i\hbar}{2m} \left( \bar \Psi \frac{\partial^2 \Psi}{\partial x^2} - \frac{\partial^2 \bar \Psi}{\partial x^2} \Psi \right) - \frac{2\Gamma}{\hbar} (\bar\Psi \Psi) = \frac{\partial}{\partial x} \left[ \frac{i\hbar}{2m} \left( \bar \Psi \frac{\partial \Psi}{\partial x} - \frac{\partial \bar \Psi}{\partial x} \Psi \right) \right] - \frac{2\Gamma}{\hbar} (\bar\Psi \Psi)
Using the definition and the formula above:
\begin{aligned} \frac{\mathrm dP}{\mathrm dt} & = \frac{\mathrm d}{\mathrm dt} \int_{-\infty}^{\infty} | \Psi(x,t)|^2 \mathrm dx = \int_{-\infty}^{\infty} \frac{\partial}{\partial x} \left[ \frac{i\hbar}{2m} \left( \bar \Psi \frac{\partial \Psi}{\partial x} - \frac{\partial \bar \Psi}{\partial x} \Psi \right) \right] \mathrm dx + \int_{-\infty}^{\infty} \frac{-2\Gamma}{\hbar} (\bar\Psi \Psi) \mathrm dx \\[12pt] & = \frac{i\hbar}{2m} \left( \bar \Psi \frac{\partial \Psi}{\partial x} - \frac{\partial \bar \Psi}{\partial x} \Psi \right) \bigg|_{-\infty}^{\infty} - \frac{2\Gamma}{\hbar}\int_{-\infty}^{\infty} |\Psi|^2 \mathrm dx = 0 - \frac{2\Gamma}{\hbar}P \end{aligned}
It is possible to solve the equation:
\frac{\mathrm dP}{\mathrm dt} = - \frac{2\Gamma}{\hbar}P
Which gives:
P(t) = e^{\frac{2\Gamma}{\hbar}t}
So the lifetime \tau is:
\tau = \frac{\hbar}{2\Gamma}