Updated EPR experiment simulation
Following my previous blog post here in which I described a program simulating the EPR experiment, I am excited to announce the release of a new version of my “Quantum Entanglement Simulation”. This latest update introduces two new preset experiments that allow users to explore deeper into the fascinating world of quantum mechanics.
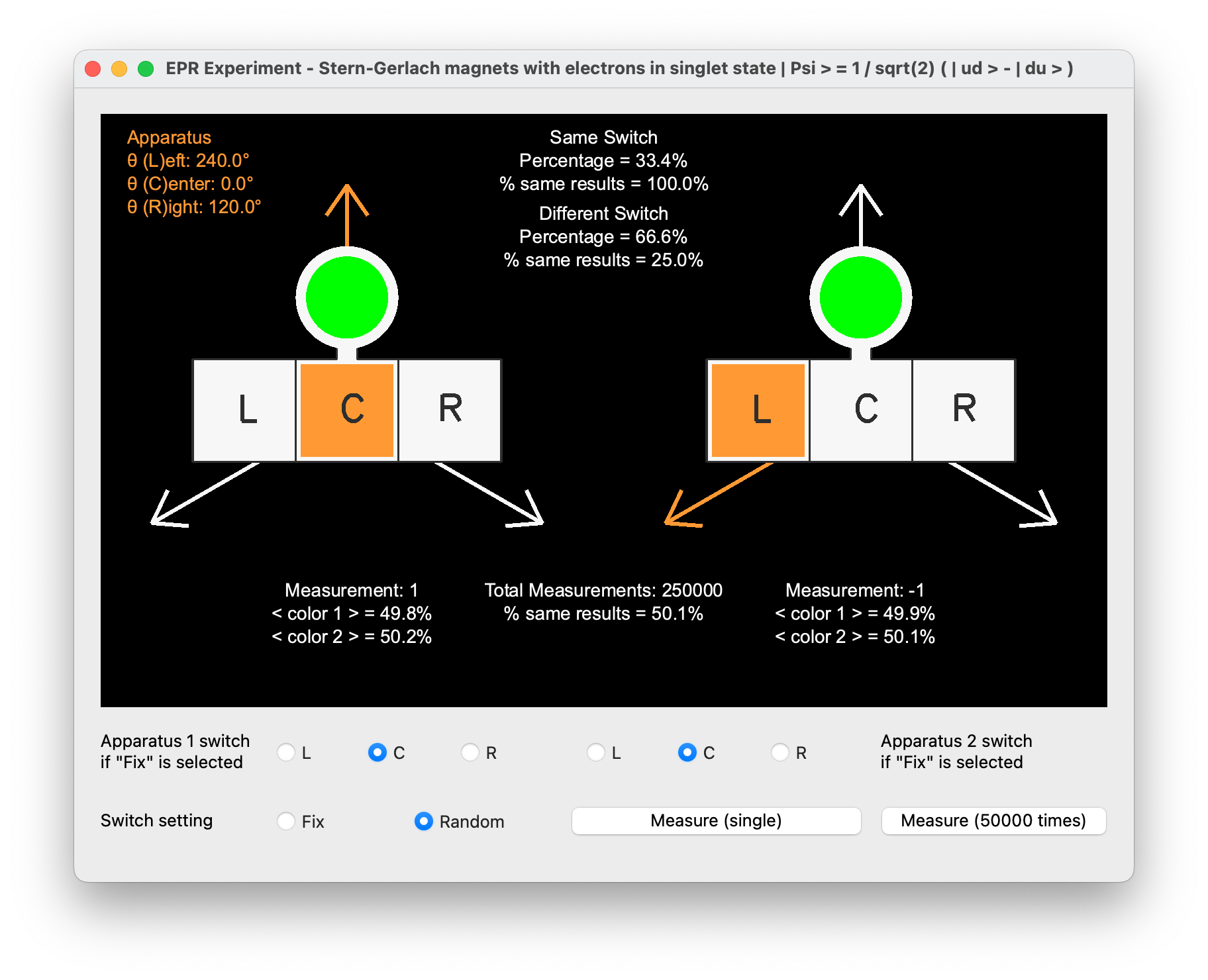
Entangled electrons with Stern-Gerlach magnets
In this experiment, the detectors are three Stern-Gerlach magnets, one oriented along the z-axis and the other two in the zx plane with ±120° rotation. The particles involved are two entangled electrons in the singlet state. The singlet state can be represented as:
| \Psi \rangle = \frac{1}{\sqrt{2}} (| ud \rangle - | du \rangle)
This setup allows for the exploration of quantum entanglement and the violation of Bell’s theorem. By measuring the spins of the entangled electrons along different axes, one can demonstrate the impossibility of hidden variables in quantum mechanics. The measurement outcomes reveal the non-classical correlations predicted by quantum theory, which cannot be explained by any local hidden variable theory.
When selecting two different detectors with a ±120° rotation, hidden variable theories predict a 33% chance that the outcomes are different. However, quantum mechanics predicts a different probability based on the angle between the detectors. Specifically, for a ±120° rotation, quantum mechanics predicts:
P = (\cos(120°))^2 = \frac{1}{4}
This means there is only a 25% chance that the outcomes are different. Experimental results consistently show a 25% probability, in alignment with quantum mechanical predictions and in contradiction to hidden variable theories. This demonstrates the accuracy and reliability of quantum mechanics in describing the behavior of entangled particles.
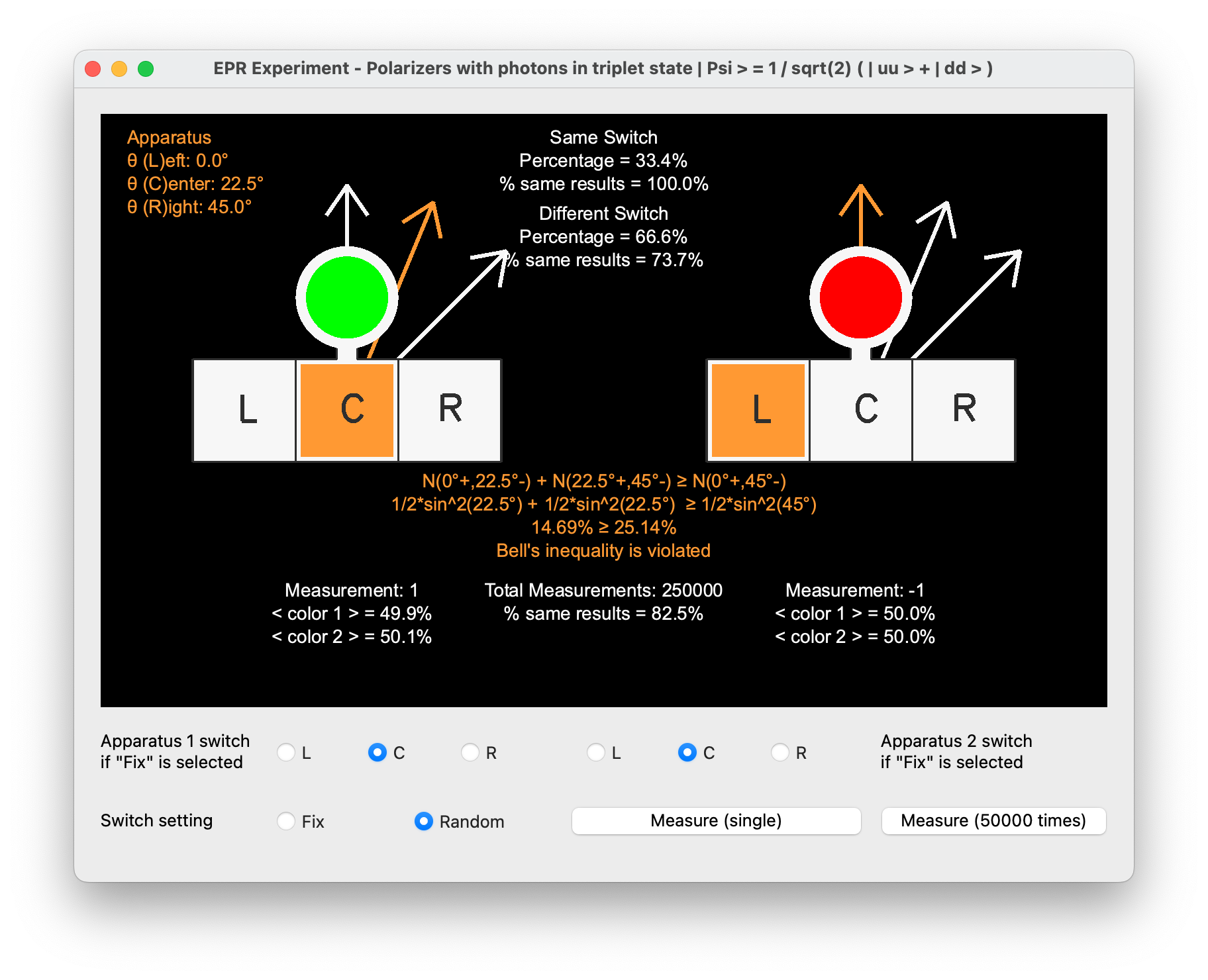
Entangled photons with polarizers
The second experiment involves an apparatus consisting of two polarizers directing two photons to three photodetectors. One photodetector is oriented along the z-axis, while the other two are in the zx plane with 22.5° and 45° rotation. The particles in this experiment are two entangled photons in the second triplet state, given by:
| \Psi \rangle = \frac{1}{\sqrt{2}} (| uu \rangle + | dd \rangle)
In the real world, light polarization is typically measured in degrees, with \theta ranging from 0° to 360°. In the Hilbert space, angles are represented by state vectors on the Bloch sphere, where \theta ranges from 0 to \pi. Since vertical and horizontal polarizations are orthogonal and correspond to π/2 in real-world measurements and π on the Bloch sphere, the relationship between the real-world polarization angle θ_real and the Hilbert space angle θ_Hilbert is given by:
\theta_{Hilbert} = 2 \times \theta_{real}
This experiment allows for a detailed examination of quantum entanglement in photonic systems. By adjusting the polarizer angles and measuring the resulting photon states, one can observe the quantum correlations that arise from entanglement. These correlations are critical for understanding the fundamental principles of quantum mechanics and have practical implications for quantum communication and computing.
This experiment mirrors the pioneering work of Alain Aspect, using entangled photons to validate the predictions of quantum mechanics via Bell’s inequalities.
The photons state indicates that the photons are simultaneously in a superposition of both being vertically polarized and both being horizontally polarized. Measurements are taken using two polarizers, P1 and P2, set at angles \theta_L and \theta_R. Each polarizer can detect polarization states, yielding outcomes of either |+1 \rangle or | -1 \rangle.
Quantum mechanics predicts the probabilities of the different measurement outcomes as:
\begin{aligned} & P_{uu}(\theta_L, \theta_R) = P_{dd}(\theta_L, \theta_R) = \frac{1}{2} \cos^2(\theta_L - \theta_R) \\ & P_{ud}(\theta_L, \theta_R) = P_{du}(\theta_L, \theta_R) = \frac{1}{2} \sin^2(\theta_L - \theta_R) \end{aligned}
For this experiment, I used polarizer settings at 0°, 22.5°, and 45° to test Bell’s inequality:
N(0_u^\circ, 22.5_d^\circ) + N(22.5_u^\circ, 45_d^\circ) \geq N(0_u^\circ, 45_d^\circ)
Here are the probabilities for these specific angles:
\begin{aligned} & P_{ud}(0^\circ, 22.5^\circ) = \frac{1}{2} \sin^2(22.5^\circ) = \frac{1}{2} \sin^2(\frac{\pi}{8}) \approx 0.073 \\ & P_{ud}(22.5^\circ, 45^\circ) = \frac{1}{2} \sin^2(22.5^\circ) = \frac{1}{2} \sin^2(\frac{\pi}{8}) \approx 0.073 \\ & P_{ud}(0^\circ, 45^\circ) = \frac{1}{2} \sin^2(45^\circ) = \frac{1}{2} \sin^2(\frac{\pi}{4}) = 0.25 \end{aligned}
Substituting these probabilities into Bell’s inequality:
0.073 + 0.073 \geq 0.25
Which simplifies to:
0.146 \geq 0.25
The results do not satisfy Bell’s inequality, demonstrating the non-local nature of quantum entanglement and refuting the notion of hidden variables. This empirical validation supports the comprehensive description provided by quantum mechanics for entangled states.
Enhanced user experience and performance
In addition to the new experiments, the new version includes an improved user interface and performance optimizations. The enhanced visuals and user interactions make the simulation more intuitive and engaging, while the optimized performance ensures faster simulations and reduced computational overhead. These improvements provide a smoother user experience, allowing users to focus on the intricacies of quantum phenomena without technical distractions.
Conclusion
The new preset experiments in the new version of my “Quantum Entanglement Simulation” offer exciting opportunities for exploring quantum mechanics. The entangled electrons with Stern-Gerlach magnets and the entangled photons with polarizers provide valuable insights into the nature of quantum entanglement and the violation of Bell’s theorem. These experiments, combined with the improved user experience and performance, make this update a significant step forward in quantum simulation.
For access to the complete simulation code, please visit the GitHub repository here.